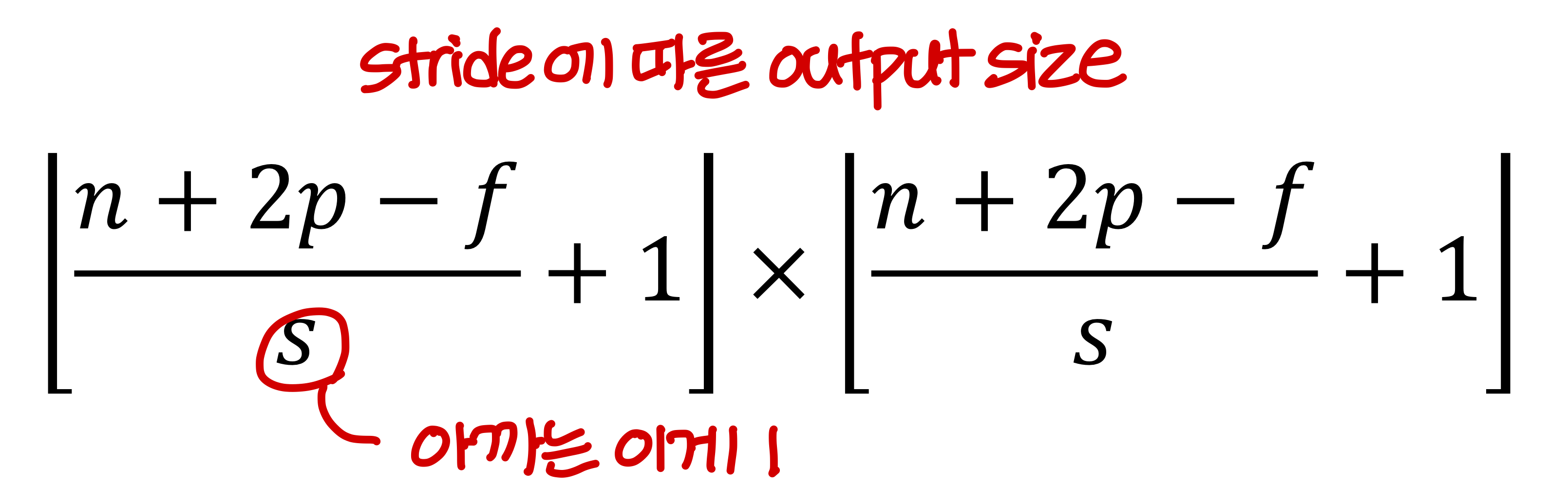Computer Vision Problem
Deep Learning on large images
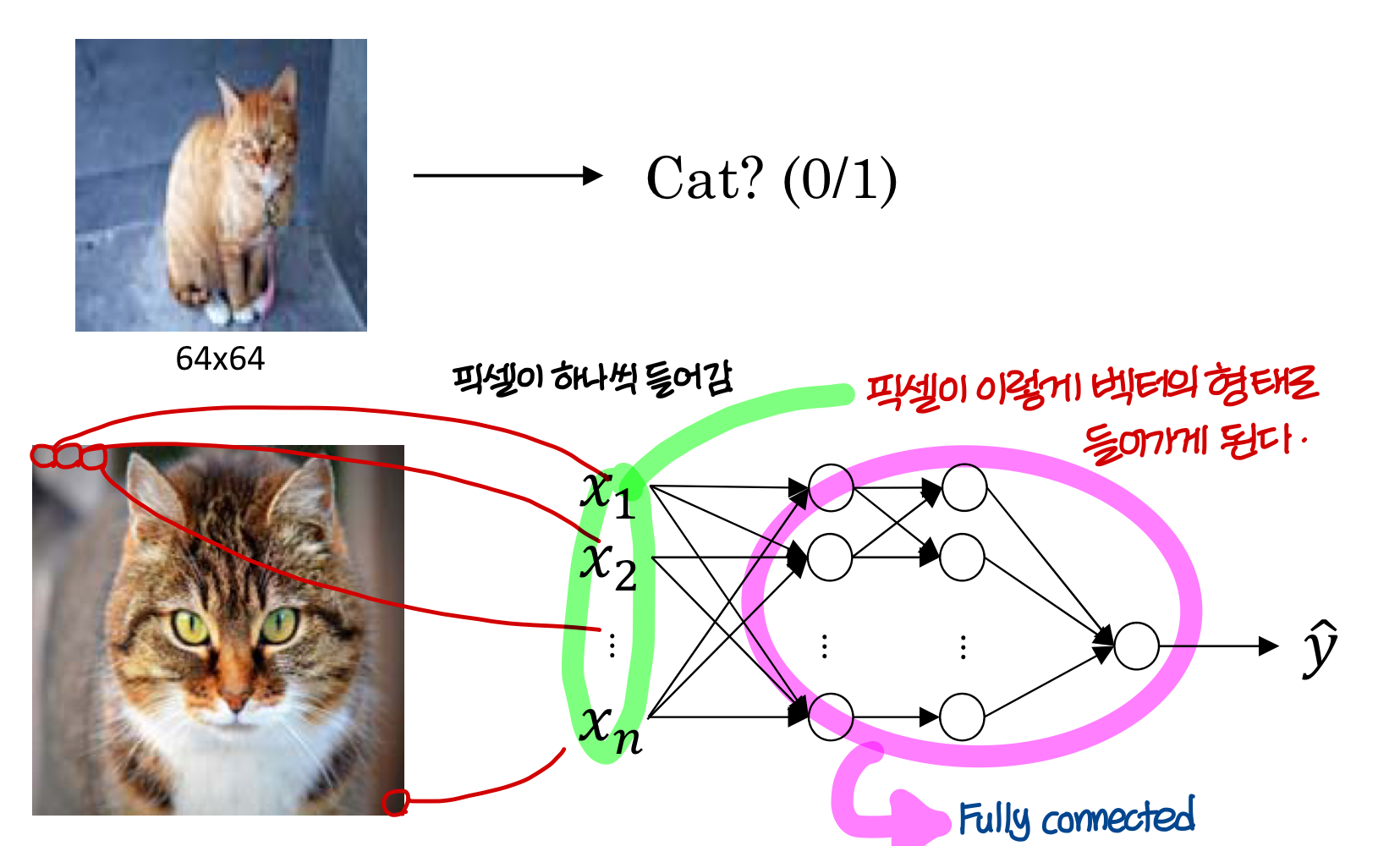
→ 근데 여기서 n의 크기는 얼마나 되는거냐? 엄청 크다!
1000X1000 이미지라면 n=1000X1000
- 그래서 이미지는 일반적으로 vector의 dimension이 큰 input을 다루는 문제이기 때문에
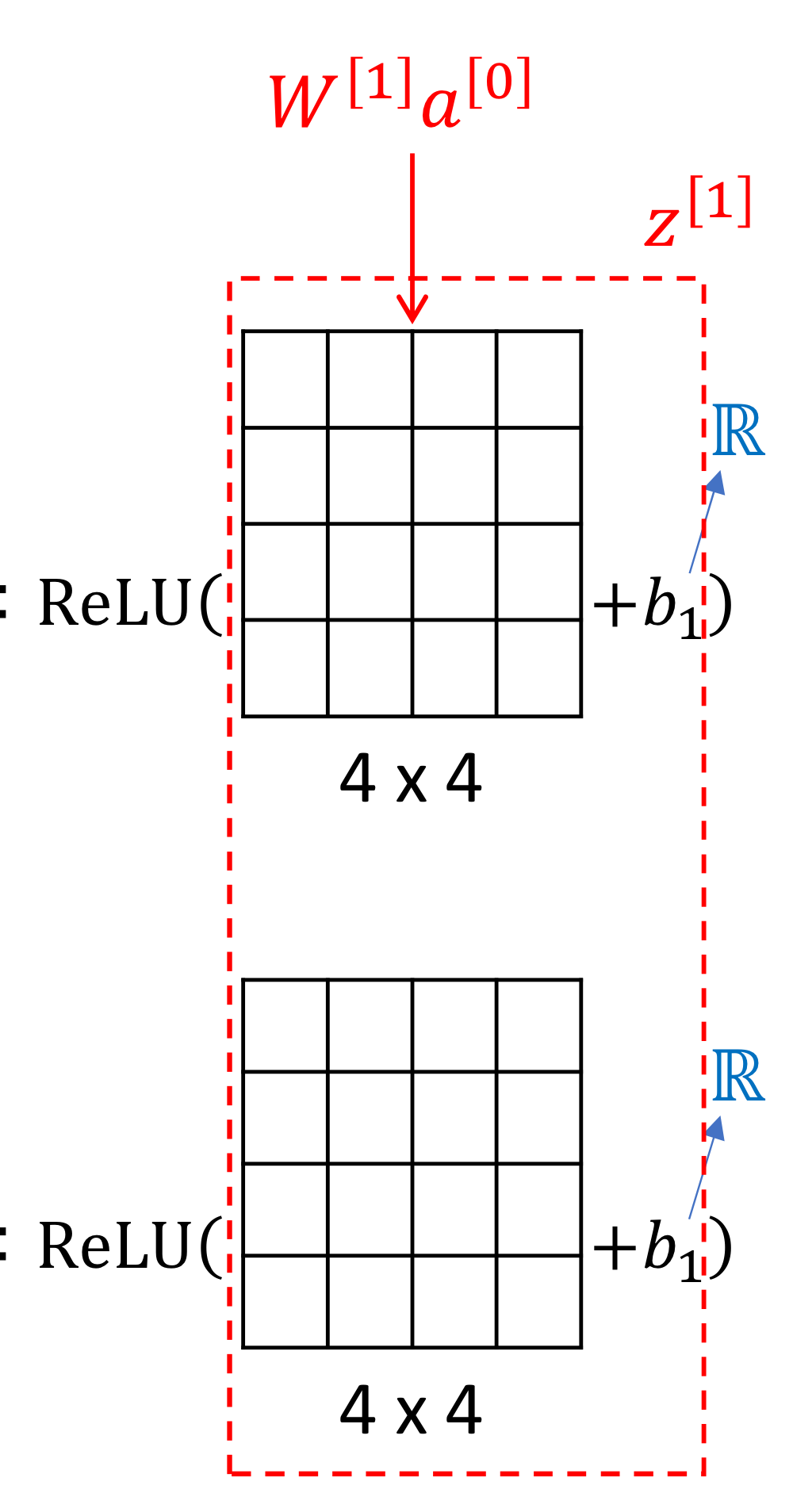
이전 layer와 이후 layer의 모든 뉴런이 연결되어 있는 fully connected로 구현하게 되면
weight의 dimension이 너무 큼!
- 그래서 training data가 보통 많은게 아니고서야
(training data 개수) < (weight matrix component 개수) 임
⇒ 이렇게 되면 underfit이 발생할 수 있음
⇒ 성능의 한계가 발생
Computer Vision Problem
- layer가 깊어질수록 classfication하는 Image featrue가 (단순→복잡)해지고
최종적으로 사람인지 아니지, 사람이라면 어떤 사람인지
이런걸 찾아내는게 CNN이다!
전통적인 Computer Vision에서는 이렇게!
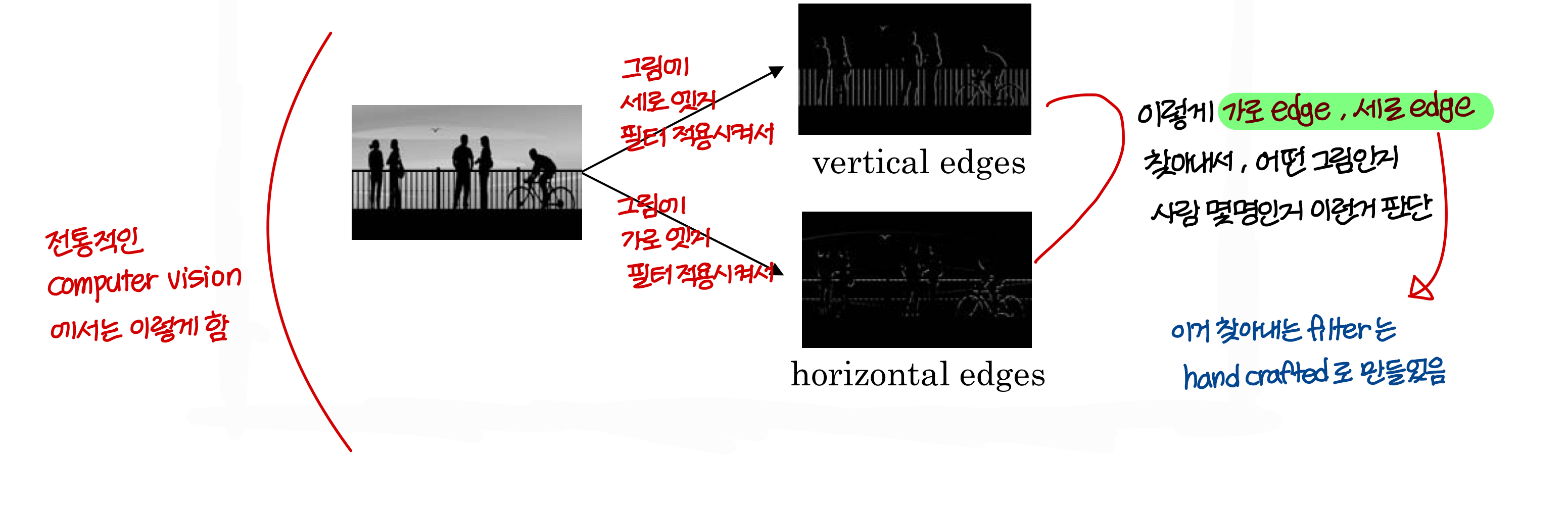
- 딥러닝에서도 이런 필터를 비슷한 개념으로 쓰긴하는데
필터를 training data를 사용해 자동으로 만든다는게
고전적인 computer vision과 다른 점임
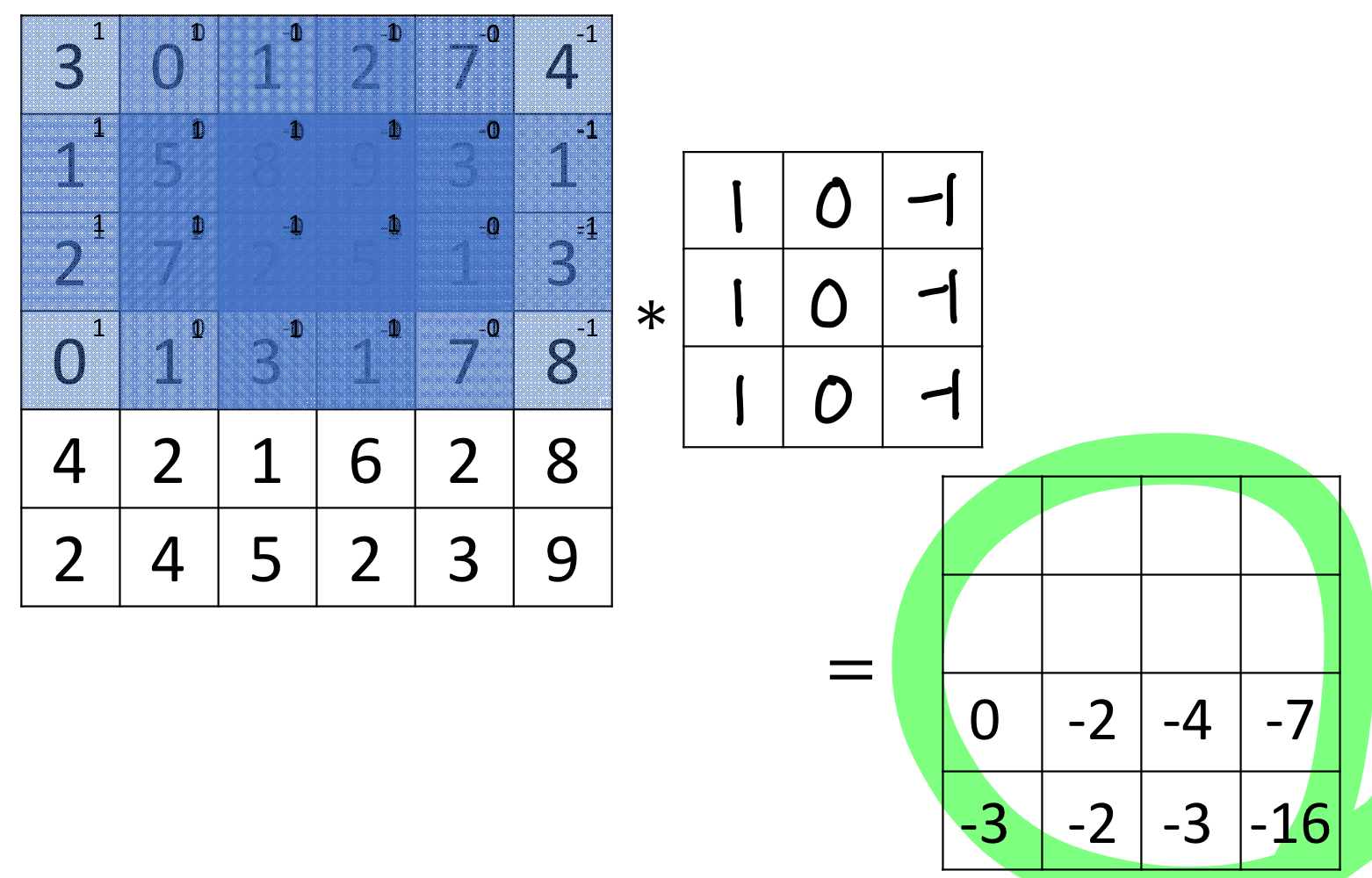
Vertical edge detection
어떤식으로 동작?
- 이런식으로 적용하다보면
→ 아래쪽에 대해서만 계산한 결과긴 하지만 결과가 이런식으로 나옴
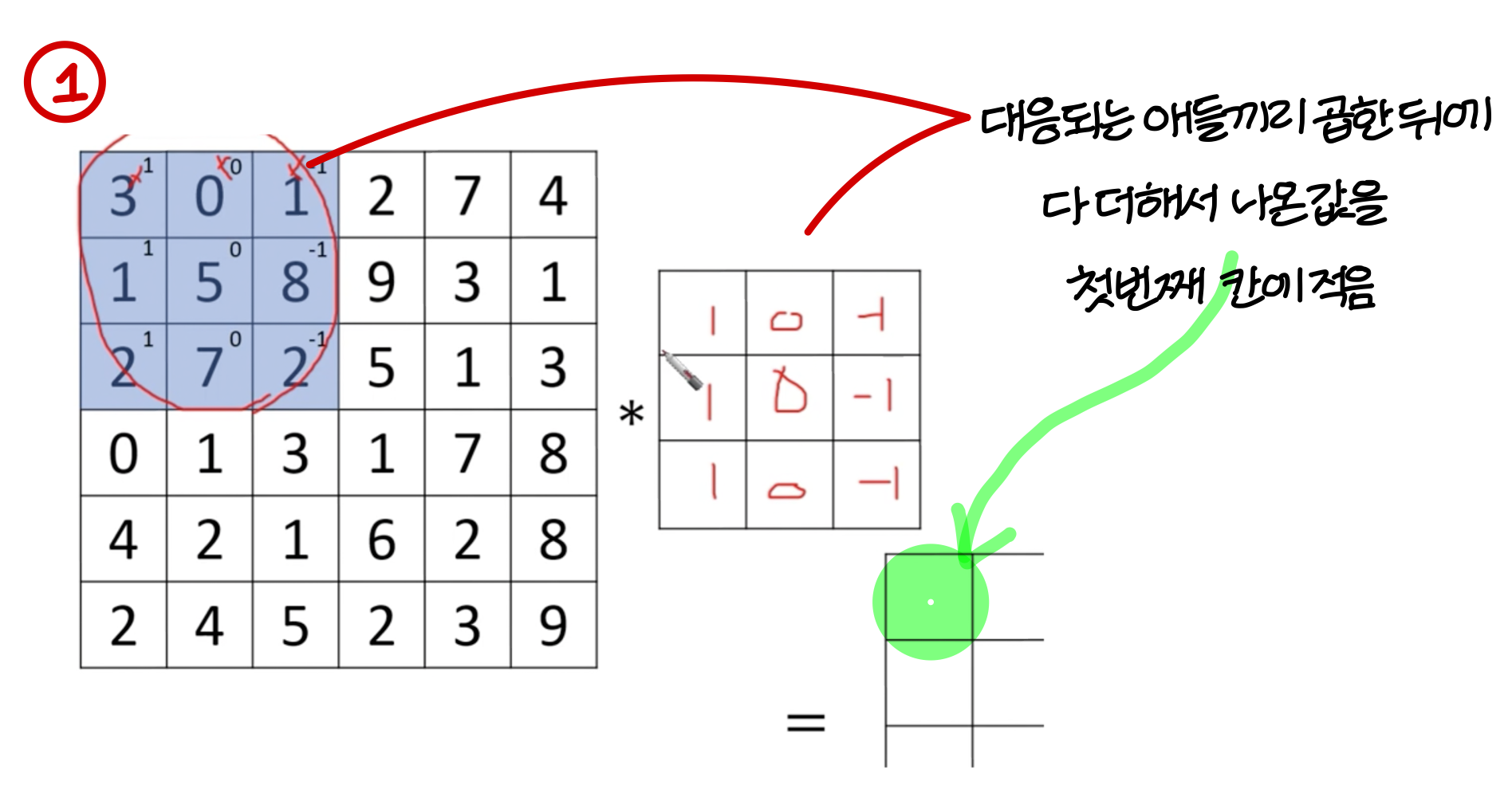
예시
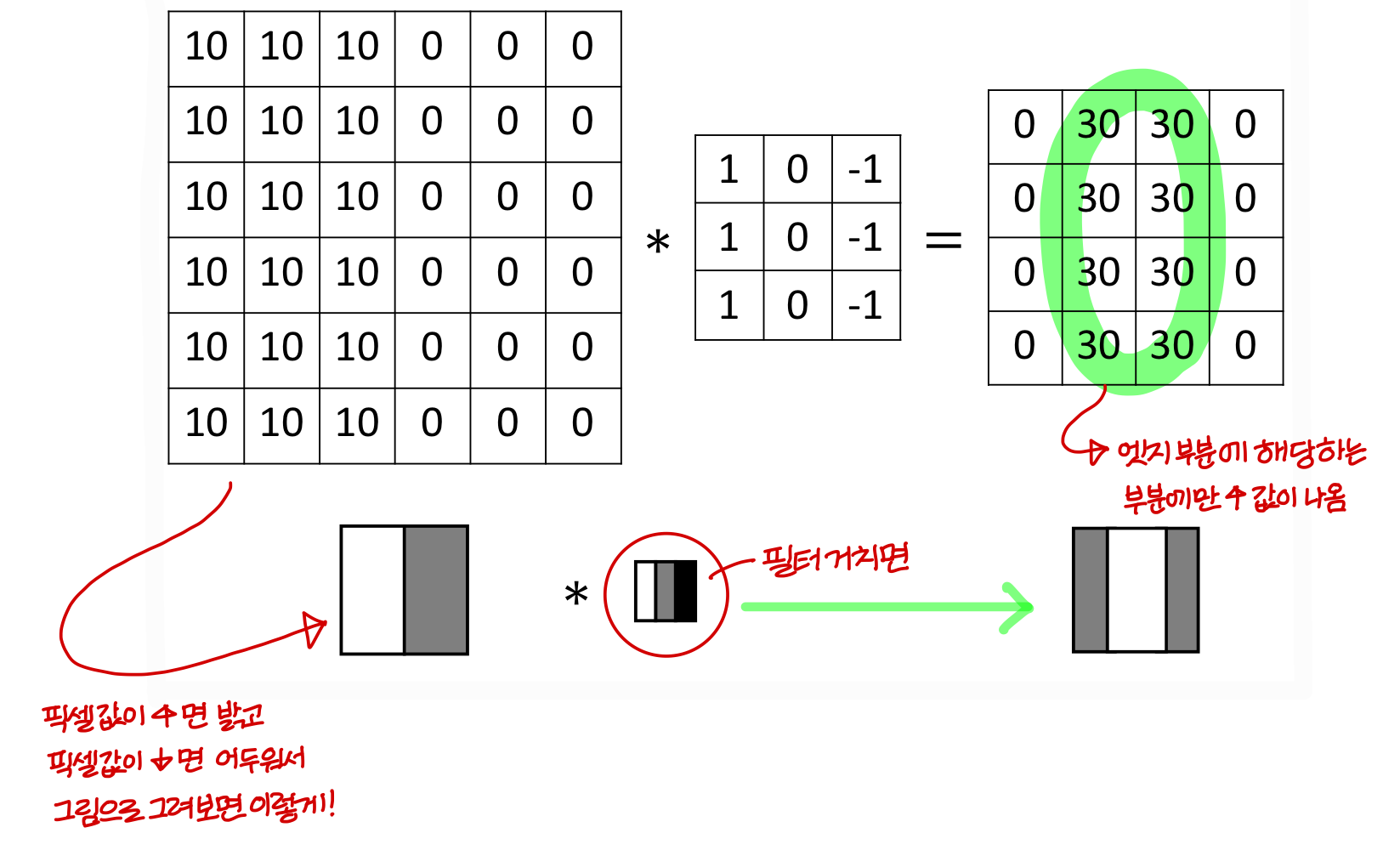
filter는 방향까지 인식함!
- (밝음 → 어두움)으로 가는 edge 부분에는 + 값이 나왔었음
- (어두움 → 밝음)으로 가는 edge 부분에는 - 값이 나온다!
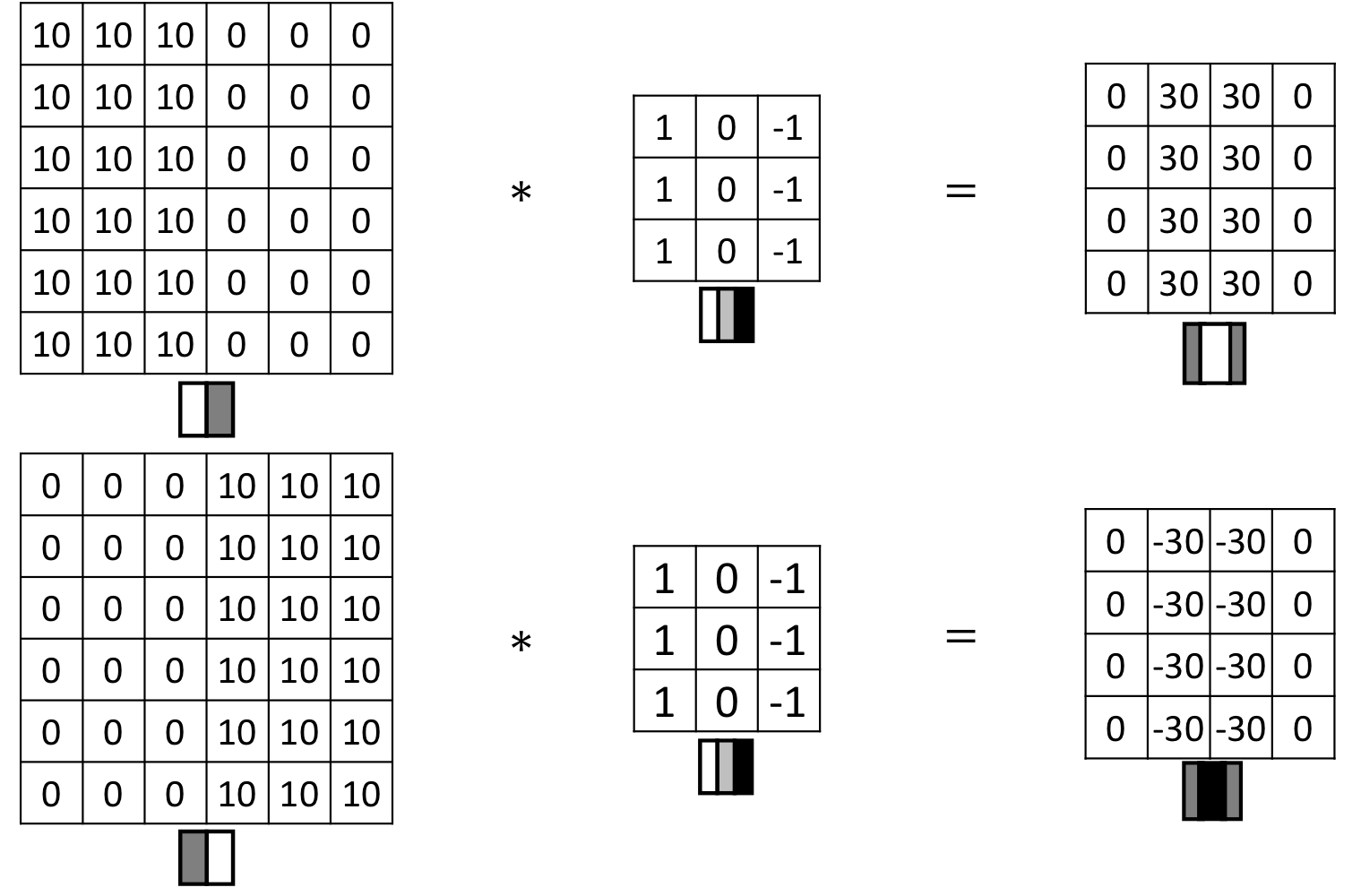
Vertical and Horizontal Edge Detection
또 다른 엣지 찾는 필터
- 이런식으로 edge를 찾아내는 mask를 filter라고 한다!
가끔씩 커널이라고도 부름
- 고전적인 vision에서는 filter를 직접 손으로 만들었음
- 그런데 edge 종류 엄청나게 다양하기 때문에 filter 손으로 일일히 만드는거 까다로움
(필터 크기 크게 하면 곡선 detect 하는 것도 만들 수 있음)
- 딥러닝에서는 이런 다양한 edge 판단하는 filter들을 자동으로 만든다
Learning to detect edges
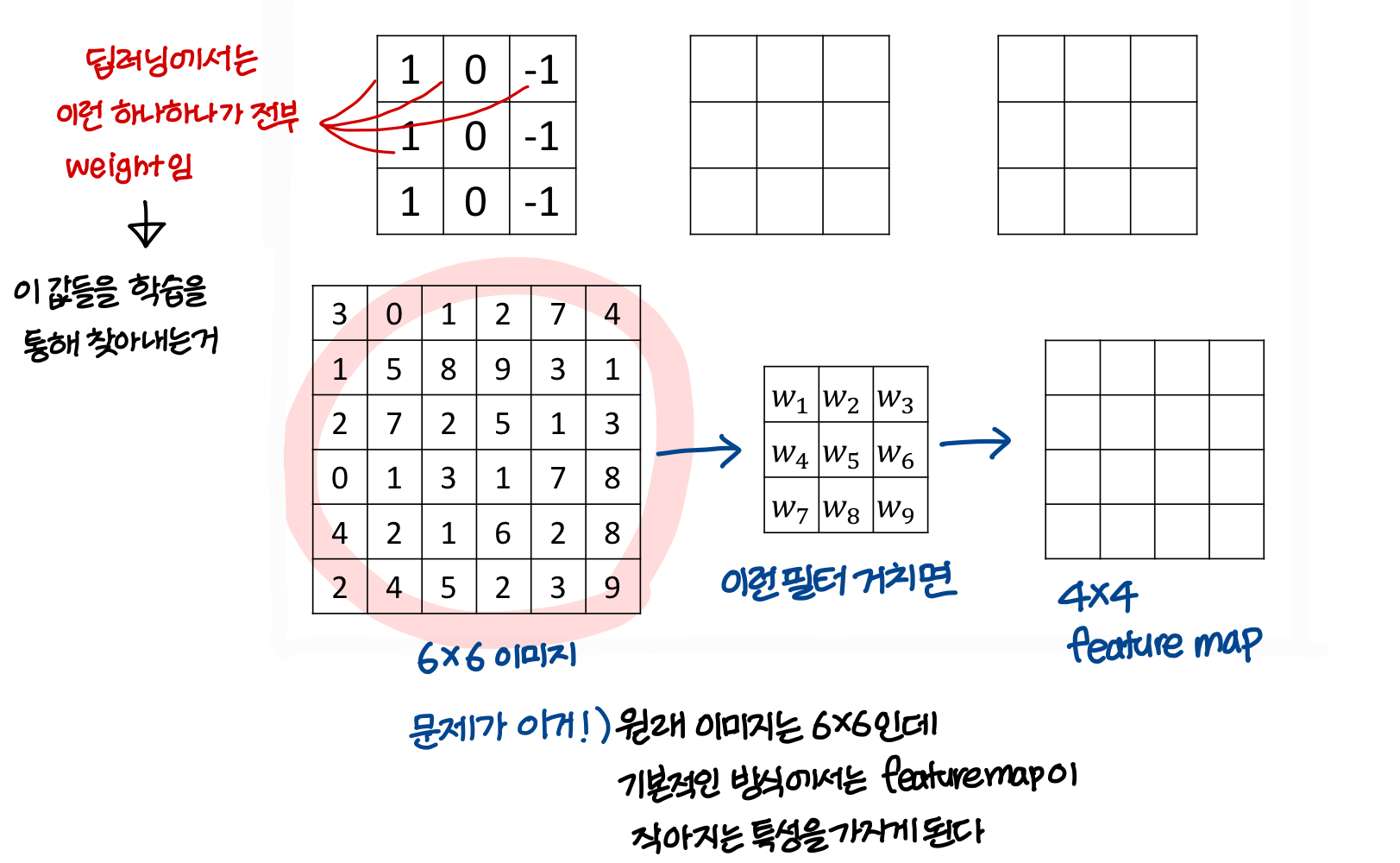
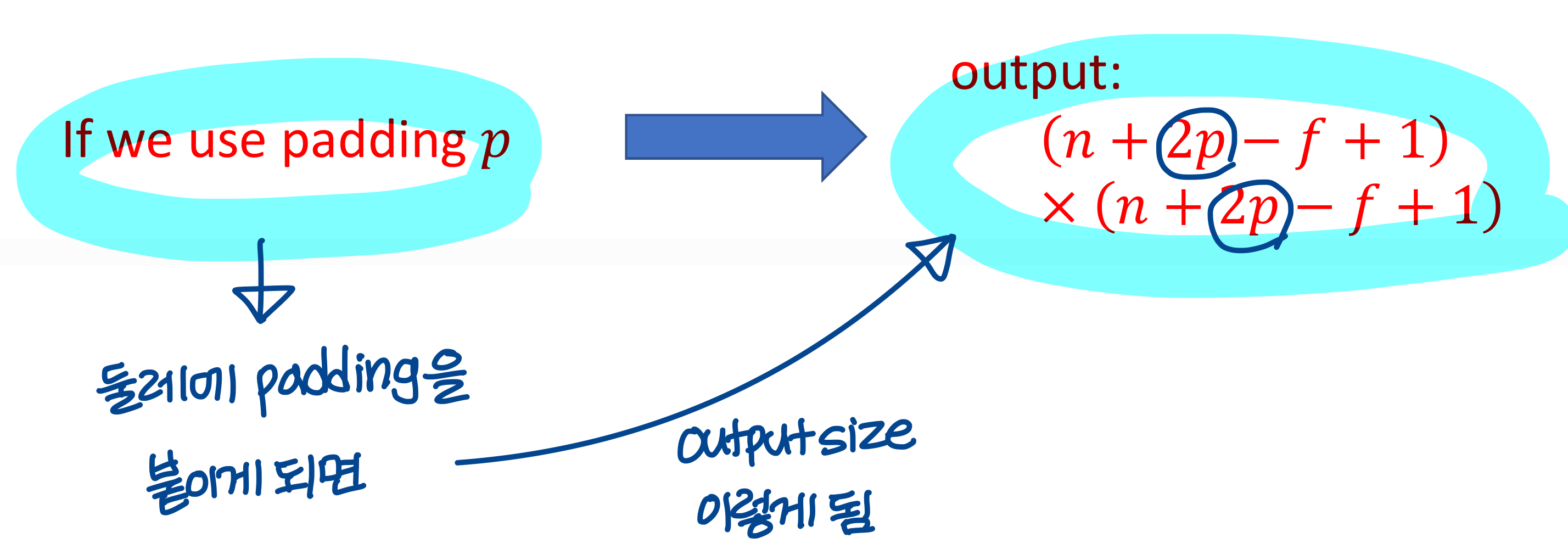
→ 작아지지 않기 위해서는 padding이라는 방법을 사용해야함
Padding
- padding 하지 않을 때 output 사이즈:
- padding 할 때 output 사이즈:
Valid and Same convolution
padding을 안하는 convolution을 valid convolution 이라고 부름
padding을 해서 사이즈를 원래 사이즈로 복원시키는 convolution을 same convolution이라고 부름→ output size와 input size가 같음
Strided convolution
- 앞에선 본 예시처럼 필터를 한칸씩 stride할 수도 있지만 여러칸 씩 stride 할 수 있음
→ 이런 convolution을
strided convolution
- strided convolution의 output size
Summary of convolutions
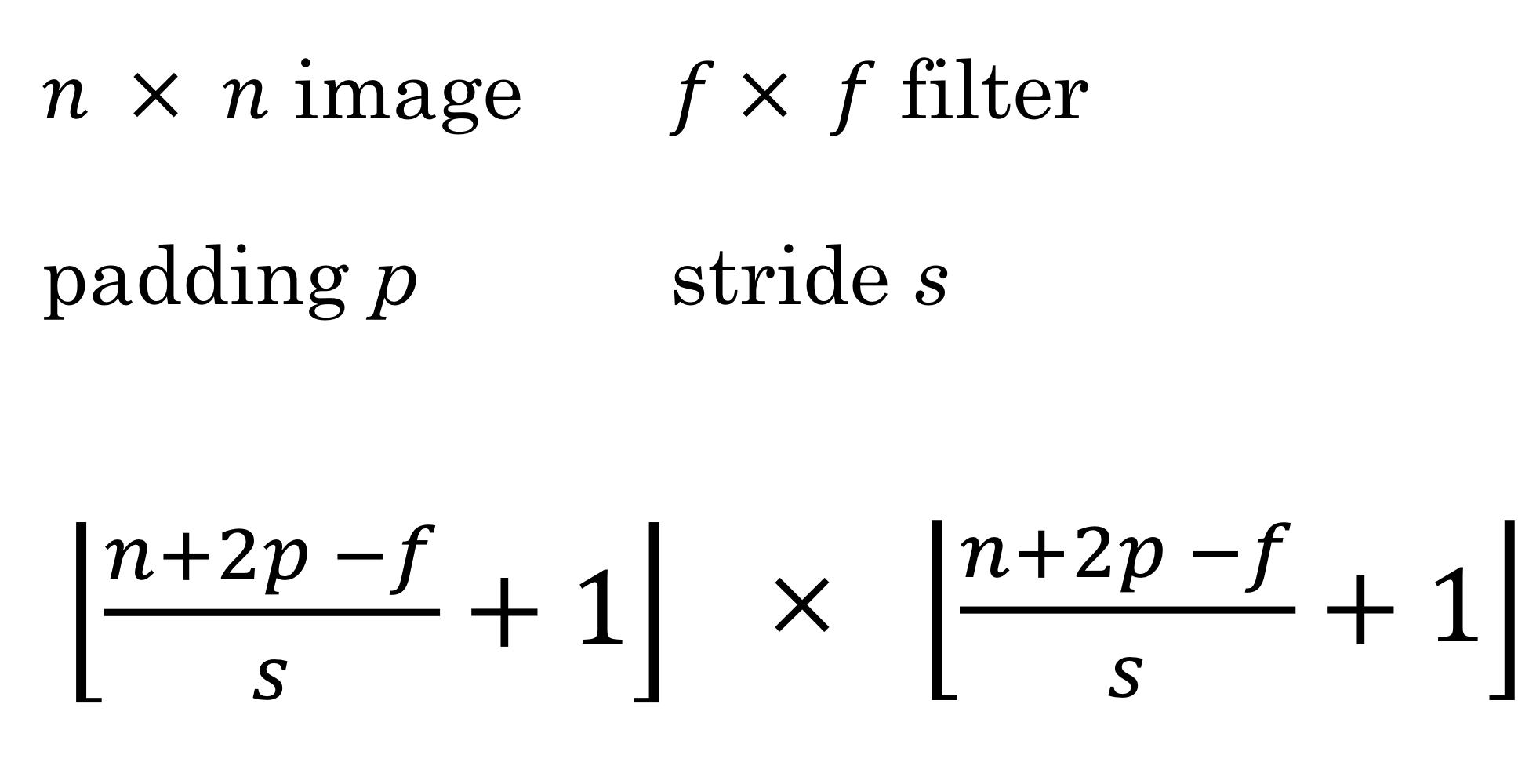
Technical note on cross-correlation vs. convolution
- 실제 signal processing에서 convolution은 순서 뒤바껴야하는거임
- 우리가 방금 본것처럼 순서 안바뀌는걸 signal processing 분야에서는 cross-correlation이라고 부른다.
Convolution in math textbook
→ 실제 signal process에서
convolution이라고 하면
이런식으로 순서 뒤바껴서 곱해질거임
Convolutions on RGB images
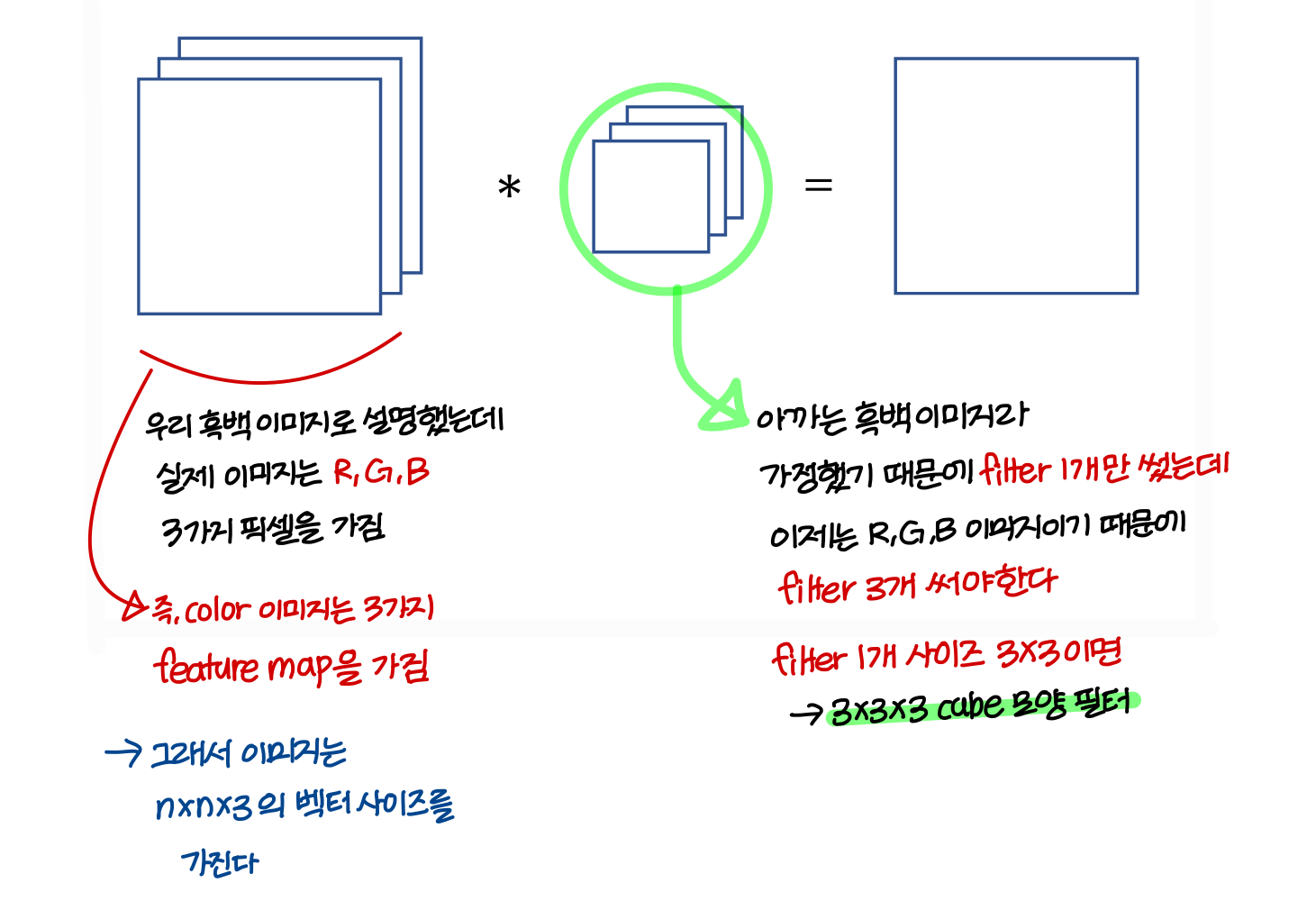
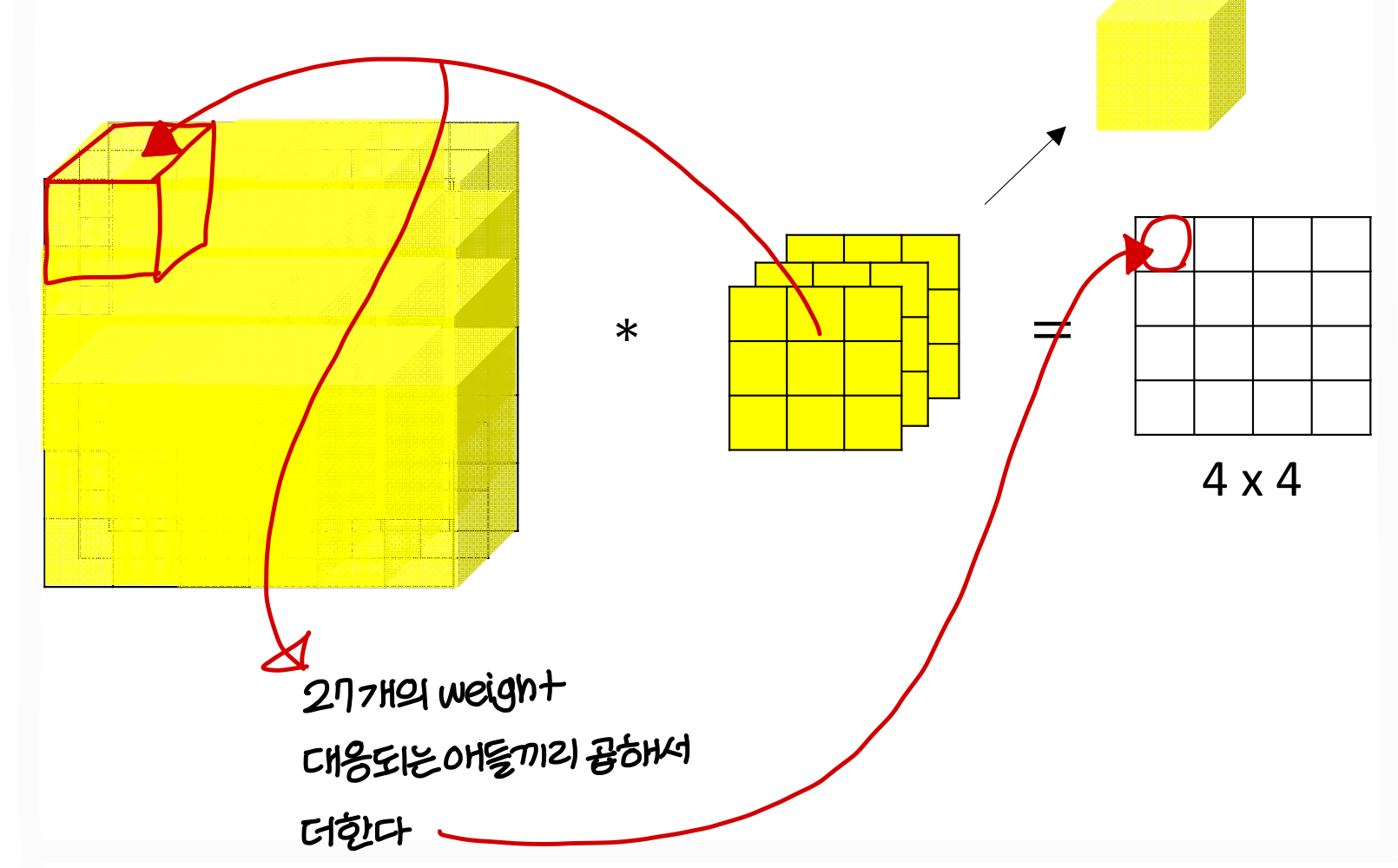
- 필터의 역할: 이미지에서 특정 stroke(선, 곡선, 꼭짓점) 이런거 찾아주는 역할을 함
→ 그런데 이미지를 구성하는 feature가 한가지만 있는게 아님
→ 여러 feature를 사용해 이미지를 detect 하는게 자연스러움
→ 따라서 feature map이 layer마다 여러개이고, filter도 여러개 사용
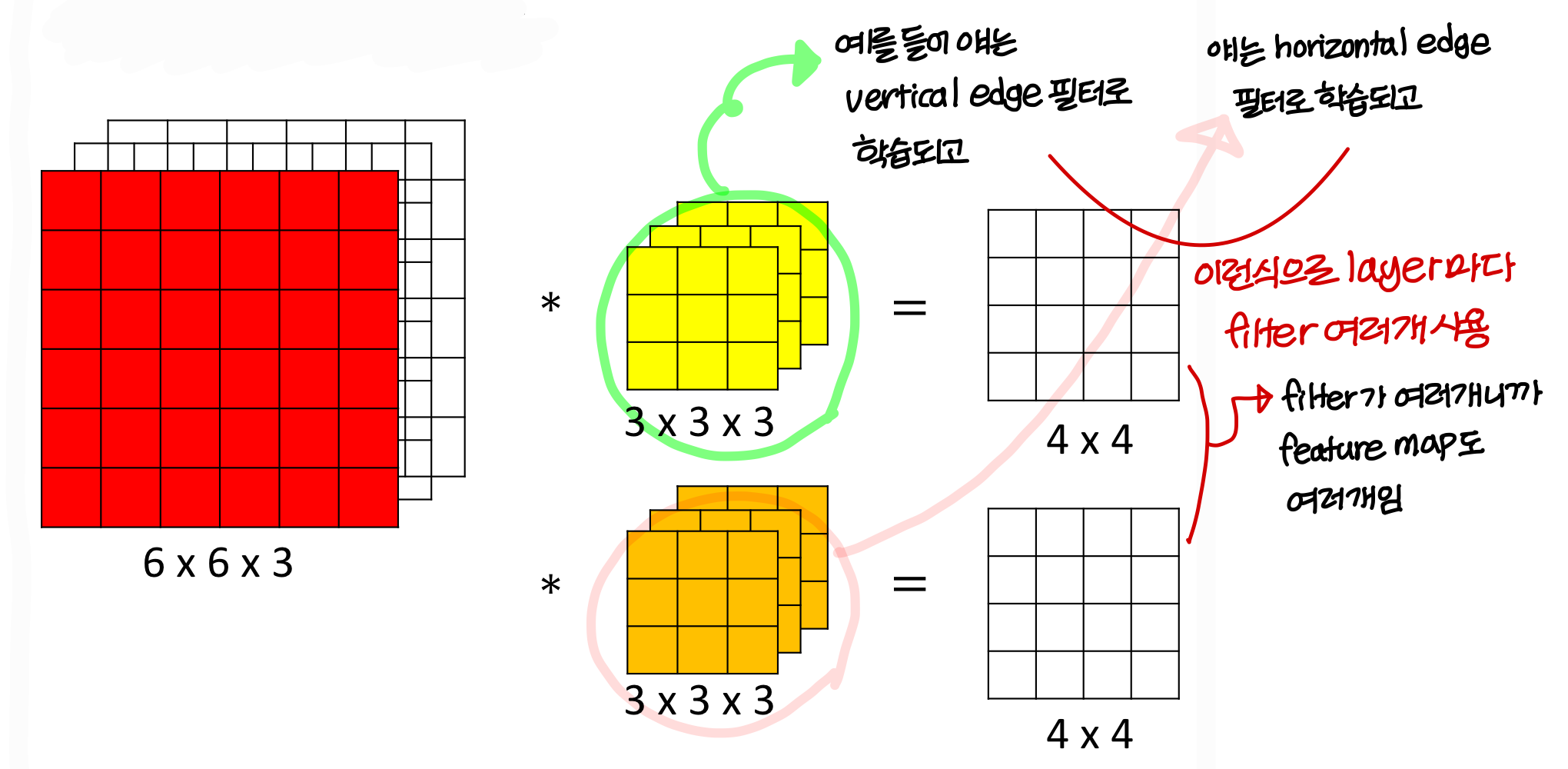
Example of a layer
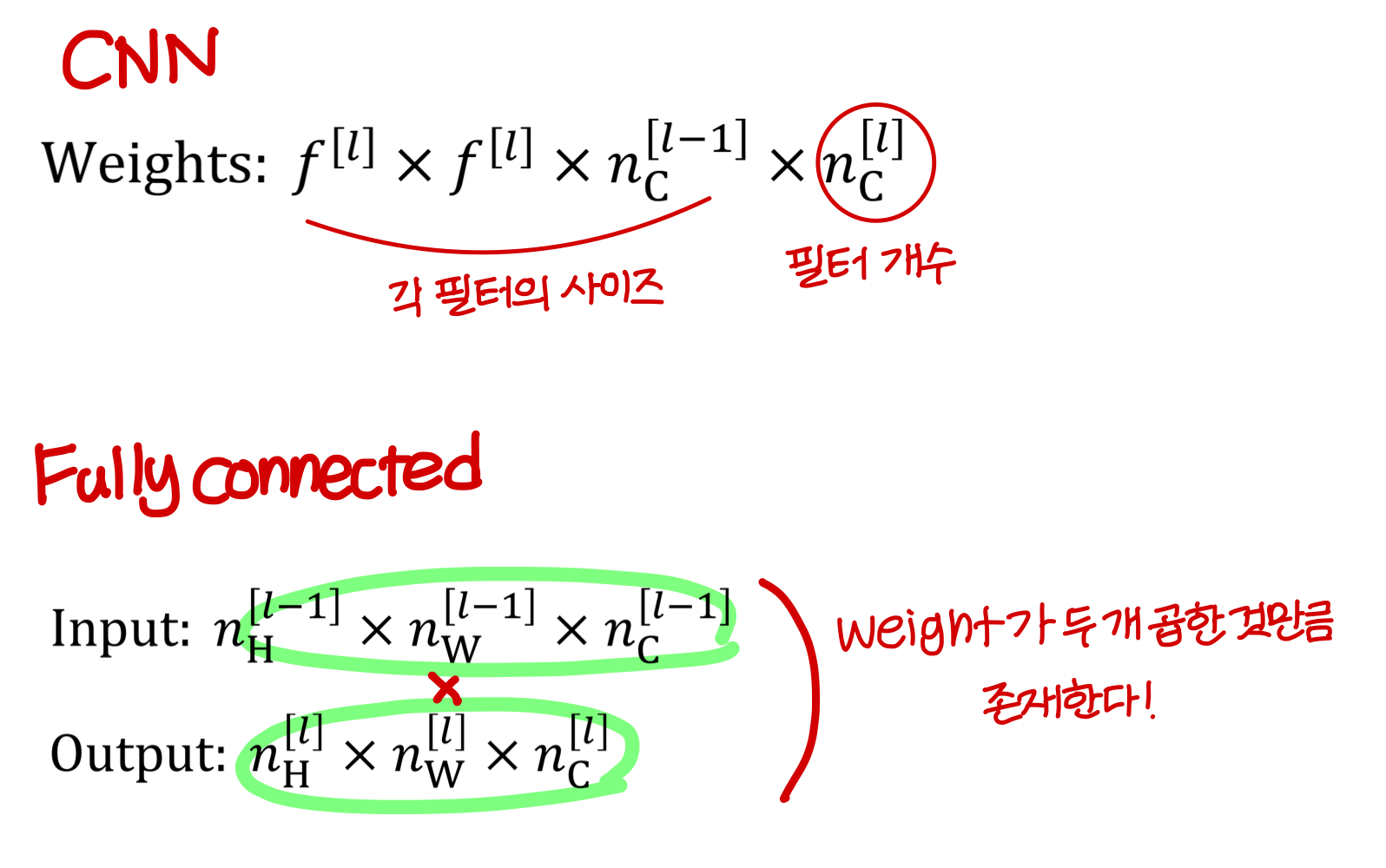
Number of parameters in one layer
- 10개의 필터를 쓰고 그 필터의 크기가 3X3X3임, neural net의 layer은 1개임
파라미터는 얼마나 필요한가?
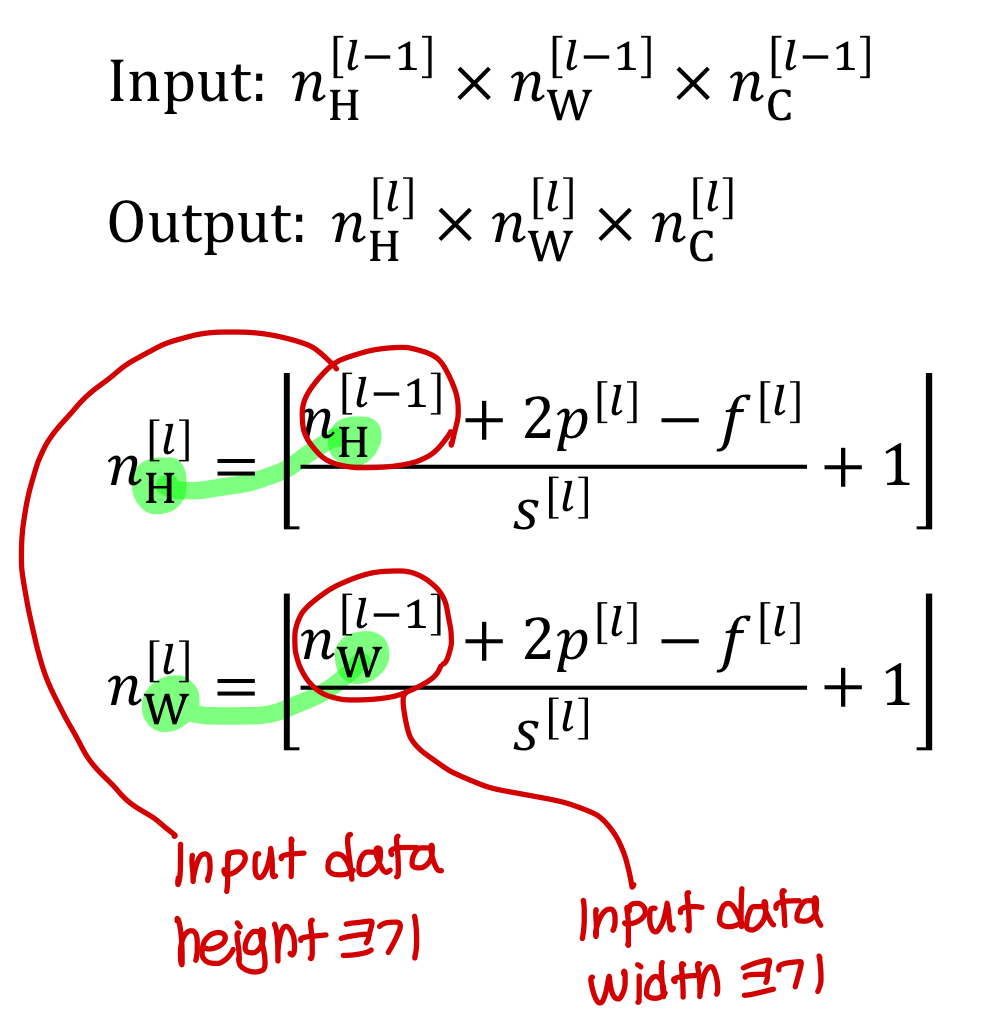
Summary of notation
layer 가 convolution layer일 때
- 이때 각 필터의 크기는?
- Input의 크기와 activation까지 통과한 output의 크기는?
- Bias는?
→ 이런식으로 filter마다 bias를 따로따로 더하니까
- CNN vs fully connected
→ 크기 차이 많이 난다. fully connected로 하면 weight matrix 크기 엄청나게 커짐
Example ConvNet
- 일반적으로 layer가 깊어지면 깊어질수록 더 high level의 feature를 학습하게 됨
그러기 위해 filter size, stride, filter 개수가 점점 많아지게 된다.
- low level은 간단한거 인식하니까 feature 개수 좀 작아도 되는데 high level은 복잡한거 인식하니까 feature 개수 많이 필요
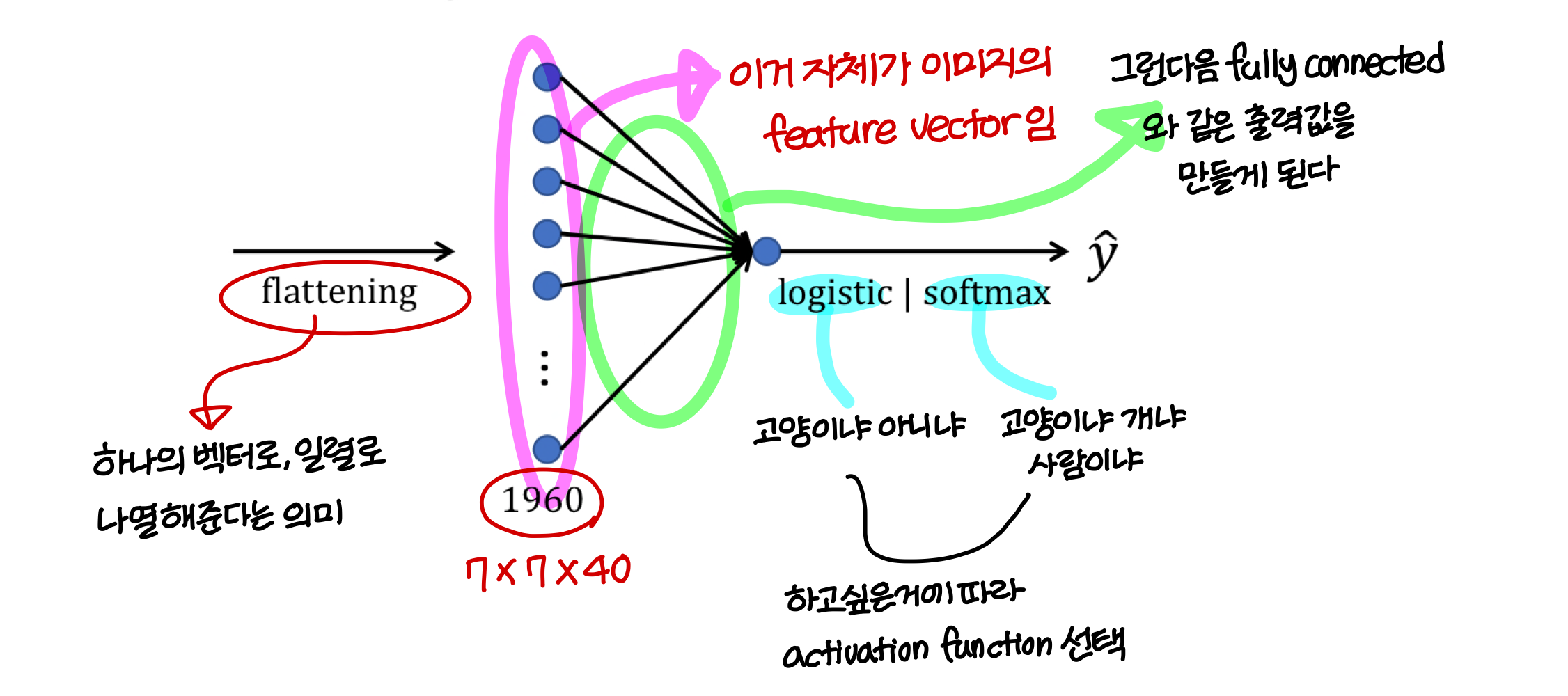
Types of layer in a convolutional network
(Convolutional network의 layer에는 3종류가 있음)
- Convolution(CONV)
- Pooling(POOL)
- Fully connected(FC)
Pooling layer
- <Max pooling>
- <Average pooling>
→ average가 의미가 있을 때 average pooling도 쓴다.
→ 정보가 좀 smoothing 되지만, 정보를 다 가져가므로 이거 쓰는 경우도 종종 있음
Summary of pooling
<pooling에서 hyperparameter는 2개!>
- f: filter size
- s: stride
- 무슨 pooling을 할지도 선택해야한다 → max or average
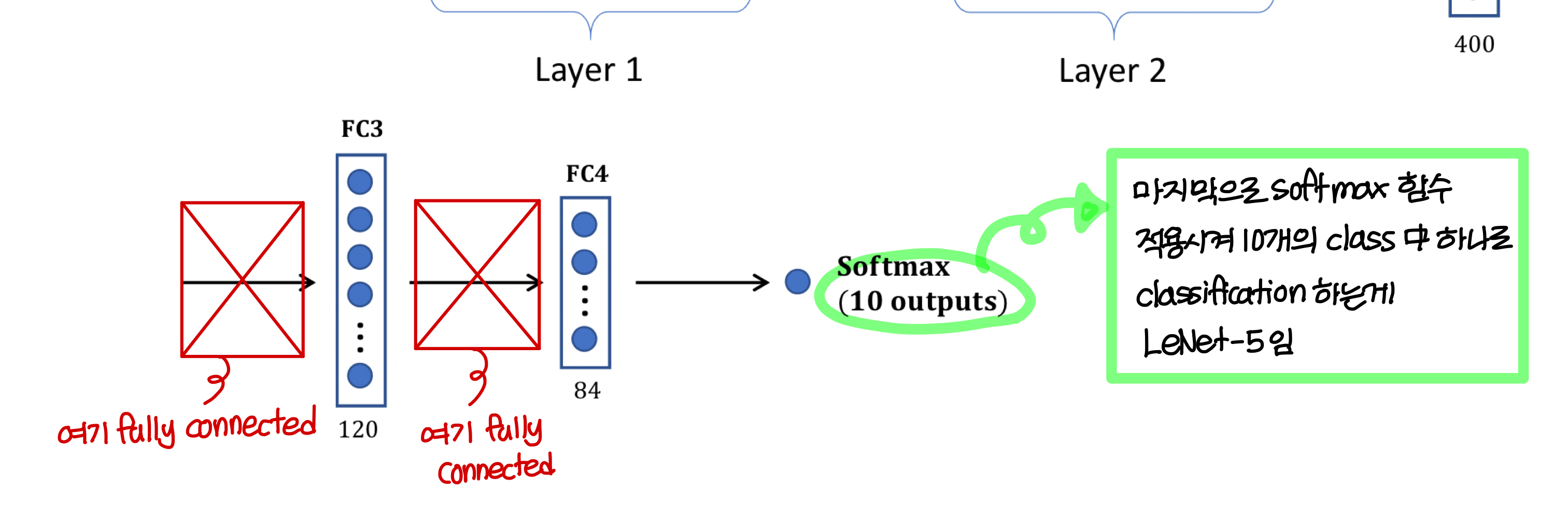
Neural network example (LeNet-5)
convolution layer, pooling layer 설명
fully-connected layer 설명
그래서 실제로 사용할 때는 모든 channel에 다 filter를 가져다 대는게 아니라 feature map 하나에 대해서만 filter 적용하고 그럼
이렇게 하면 비슷한 노력으로 훨씬 좋은 성능을 낼 수 있음
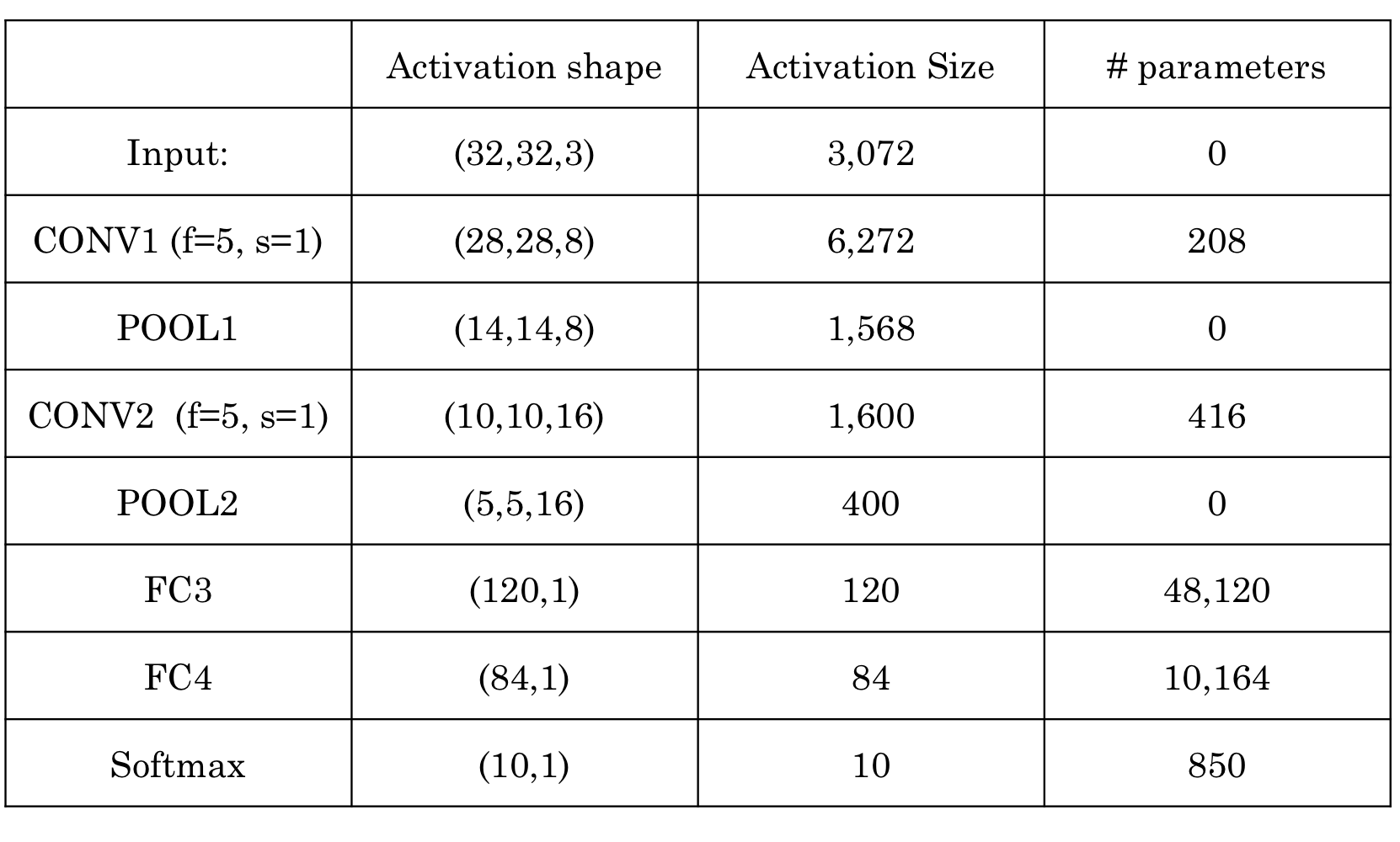
→ 위와 같이 했을 때의 activation size 및 # parameters
Why convolutions?
1) Parameter sharing
이미지 특성 자체가 같은 패턴이 반복되니까 filter(feature detector)를 share하는 CNN이랑 잘맞다!
2) Sparsity of connection
fully connection에서는 모든 값을 다 써서 output의 숫자 하나하나를 만들었음
즉 output value가 large number of input을 써서 만들어짐
그런데 CNN에서는 근처에 있는 애들끼리만 계산해서 숫자 하나하나를 만드므로
connection에 sparsity(희소성)가 있음
Putting it together
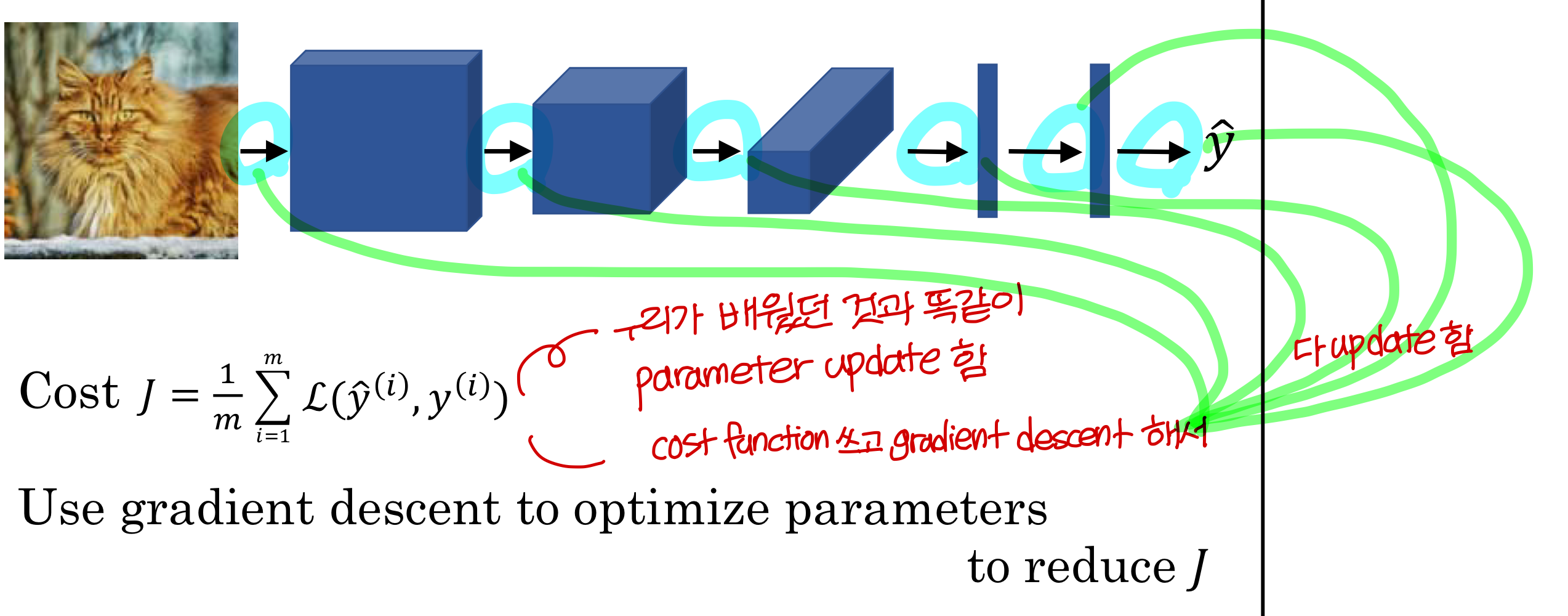
추가로 생각해보기
- 같은 패턴인데 크기가 다른 경우 있음
→
이런 경우엔 크기 별로 다 학습을 해야하나?No! 하나만 학습해도 됨!→ pooling해서 패턴의 대표값만 학습되기 때문에 큰 걸 학습했을 때 작은 것도 인식가능
→ 즉 pooling이 size에 independent하게 패턴을 인식할 수 있게 해준다
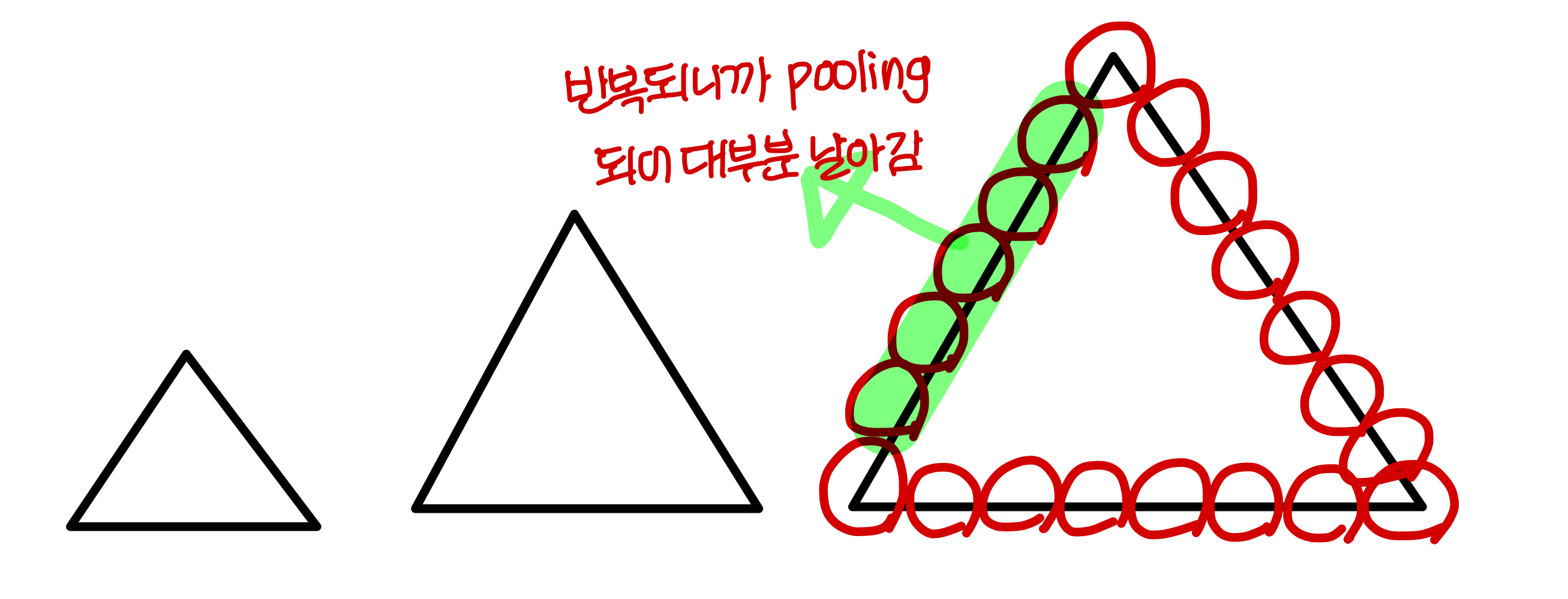
- 같은 모양인데 다른 방향
→ convolution + pooling만 있을 때는 이론적으로 방향 바뀐걸 같은걸로 판단 못함
→ 그래서 학습할 때 데이터를 뻥튀기해서 다양한 방향의 패턴을 학습해야함
Uploaded by N2T