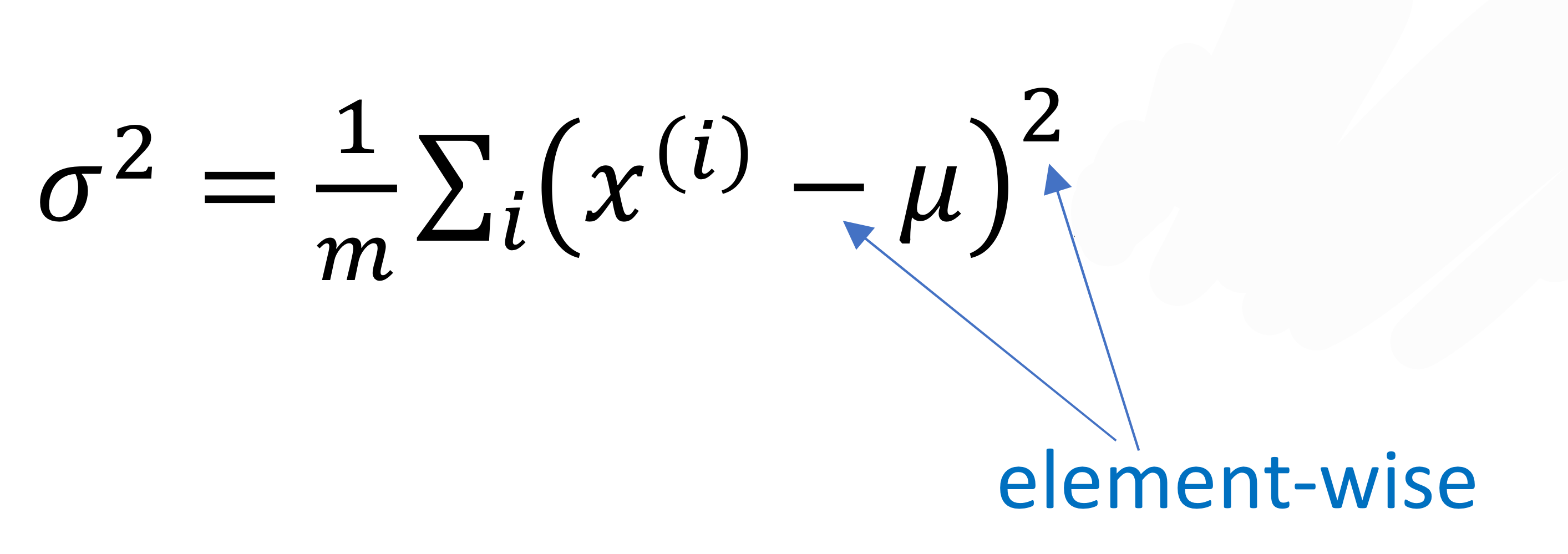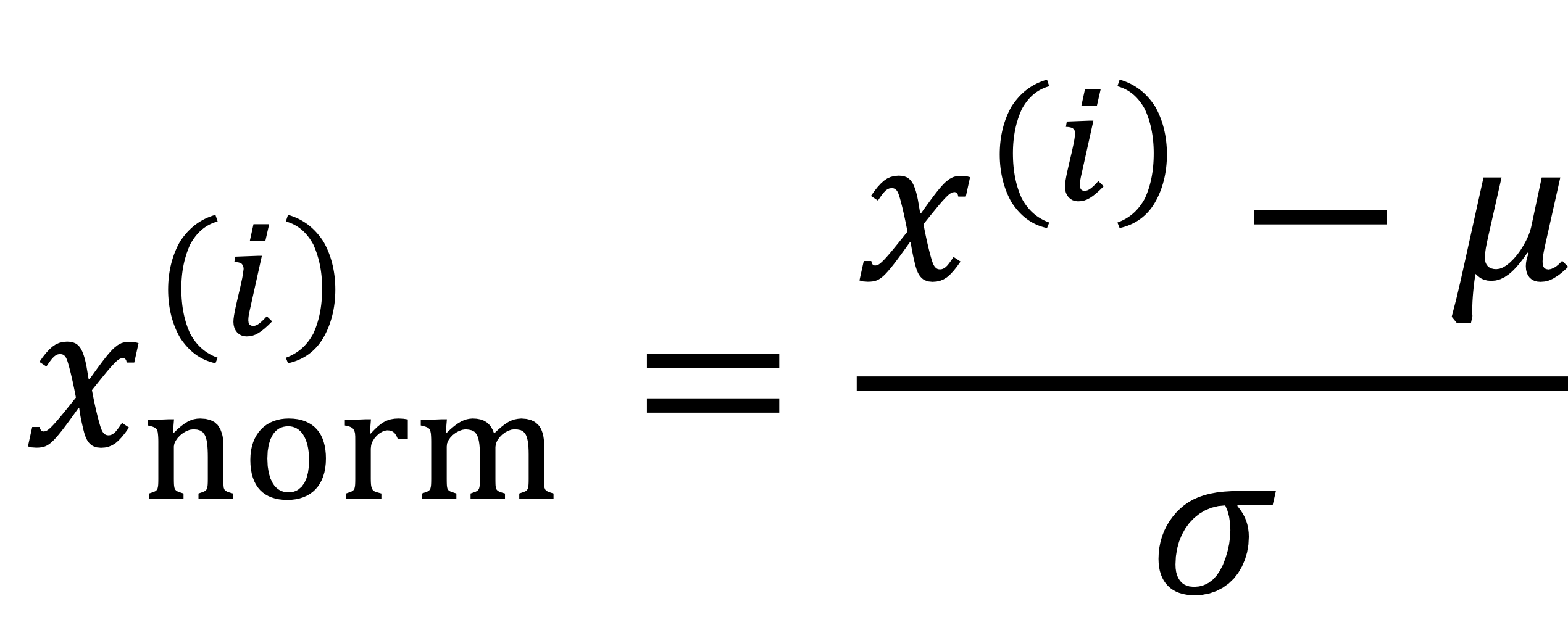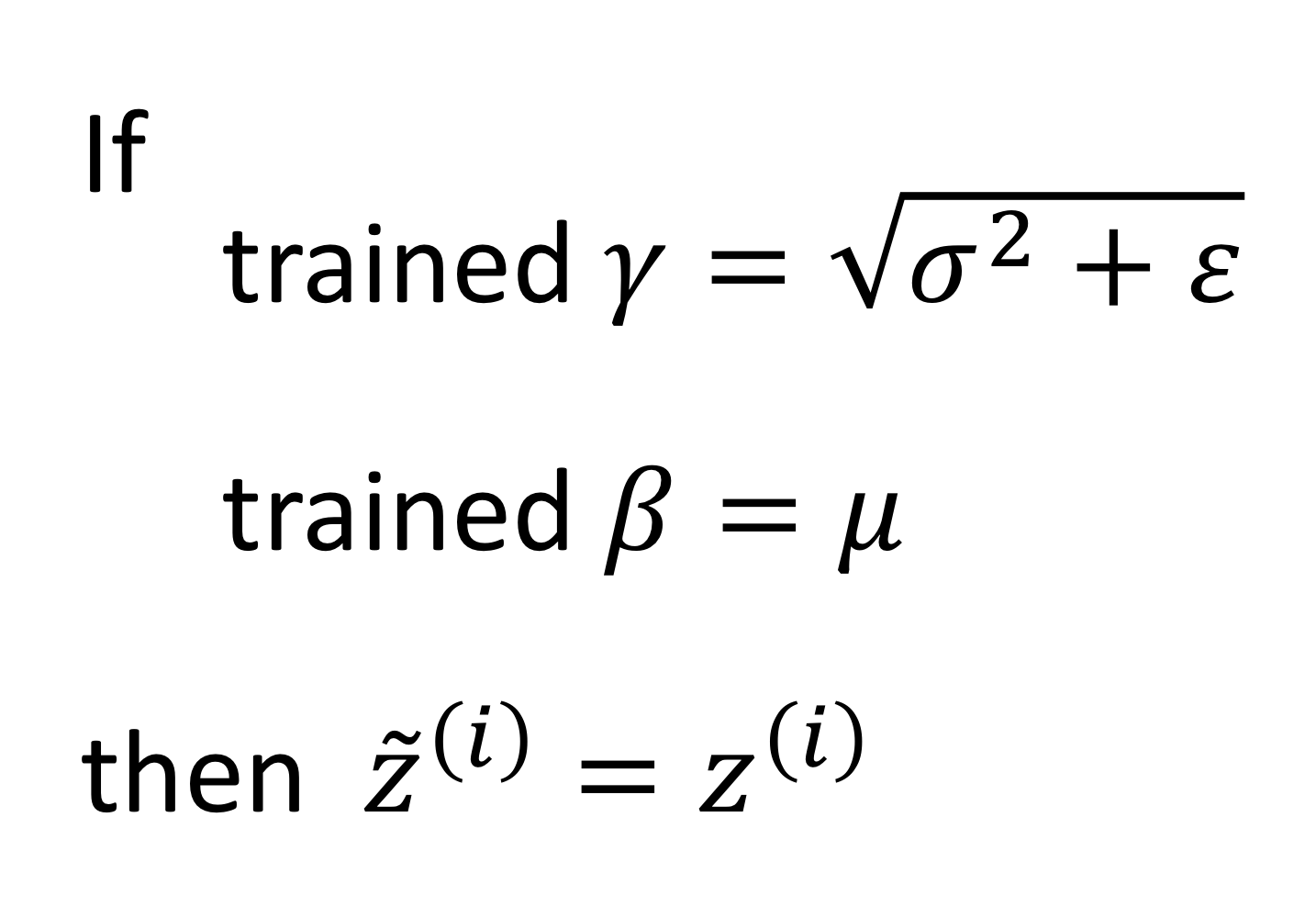Hyperparmeters

Try random values: Don’t use a grid
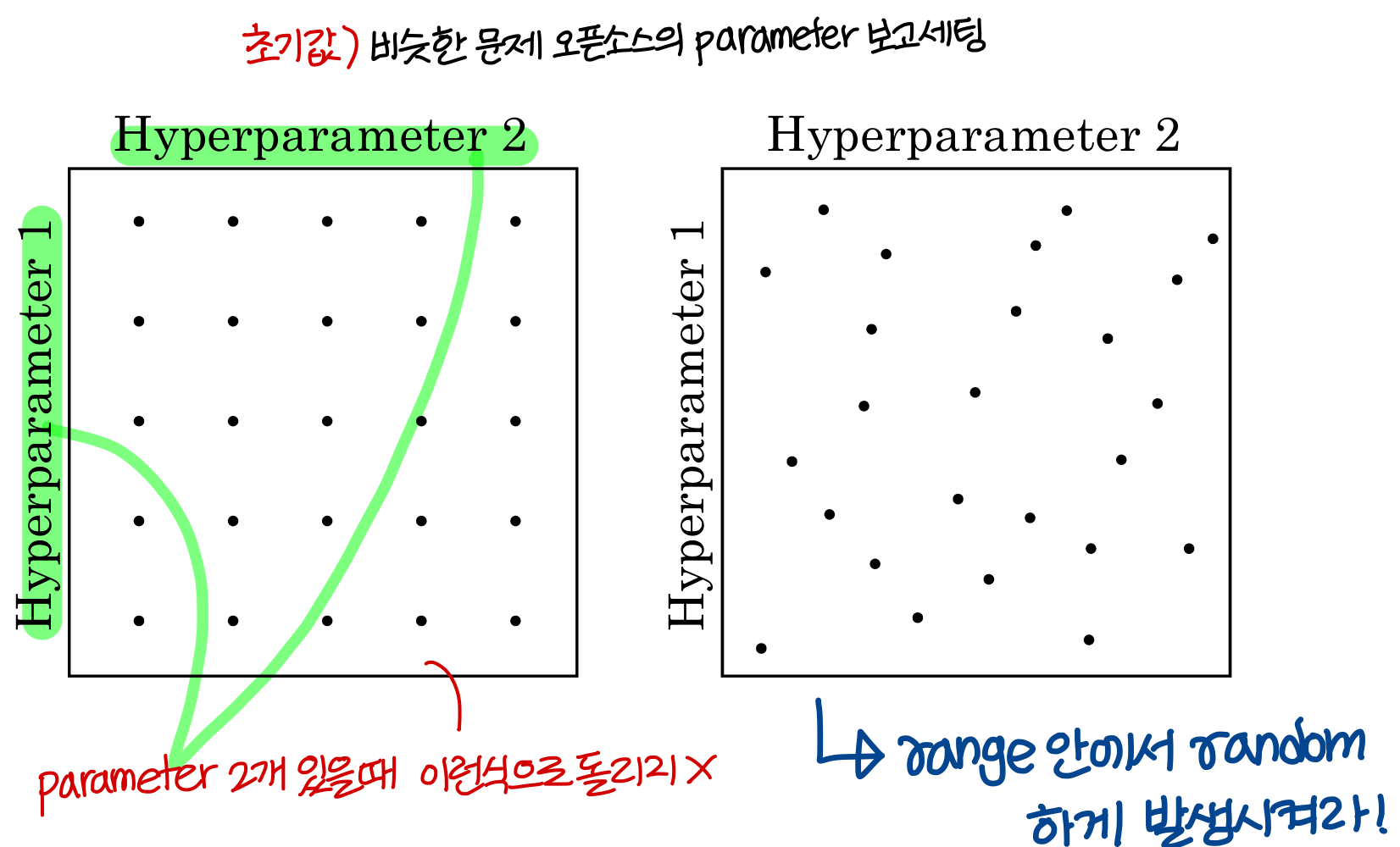
→ 왼쪽처럼 grid 형태로 parameter를 발생시키지 마라!
→ 오른쪽 처럼 random하게 parameter를 발생시켰을 때 성능 좋은 parameter를 더 빨리 찾을 수 있다.
Coarse to fine
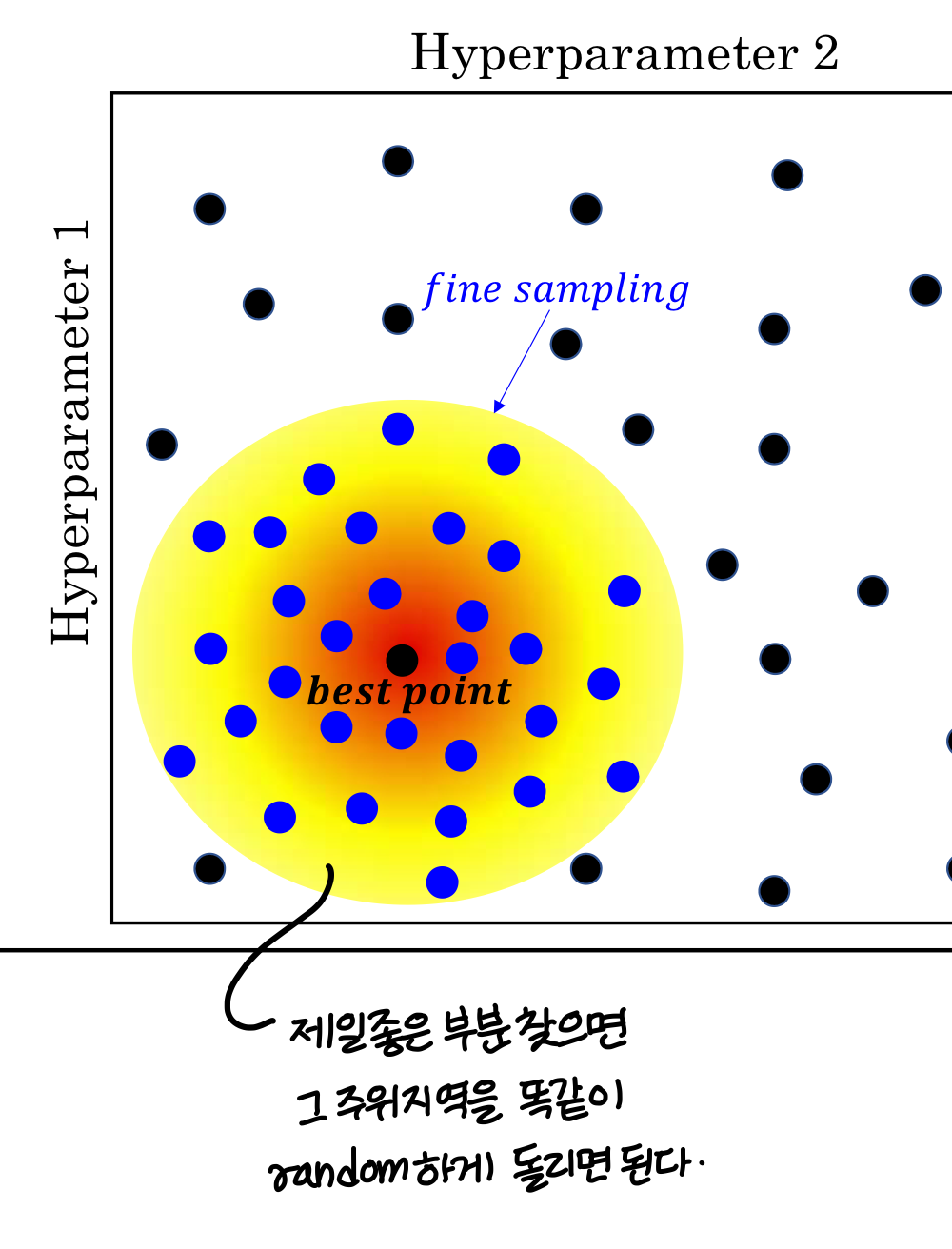
Appropriate scale for hyperparameter

Hyperparmeters for exponentially weighted averages
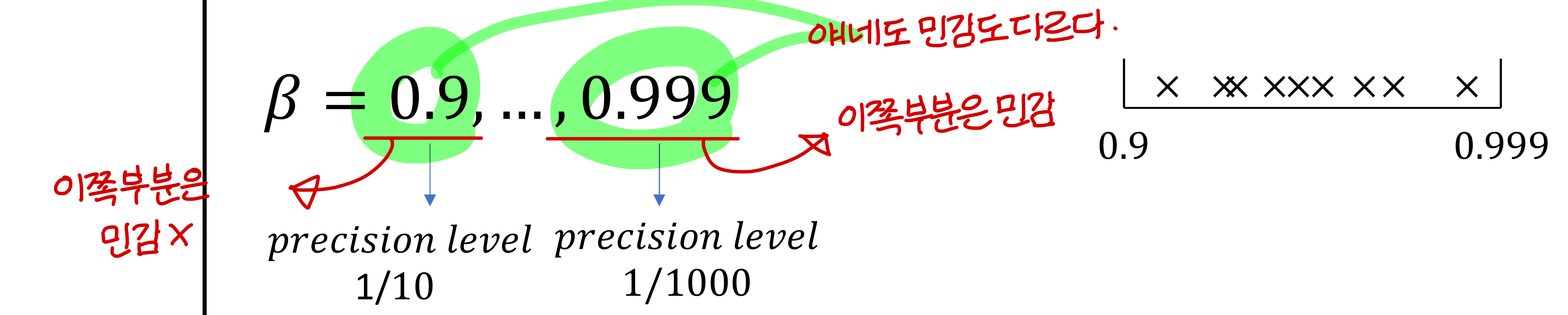
→ β 가 0.9~0.9005 사이일 때는 별로 안중요함. 정밀하게 세팅할 필요가 없음
→ β 가 0.9990~0.9995 사이일 때는 숫자 조금만 움직여도 엄청나게 변화. 정밀하게 세팅해야함
Re-test hyperparmeters occasionally
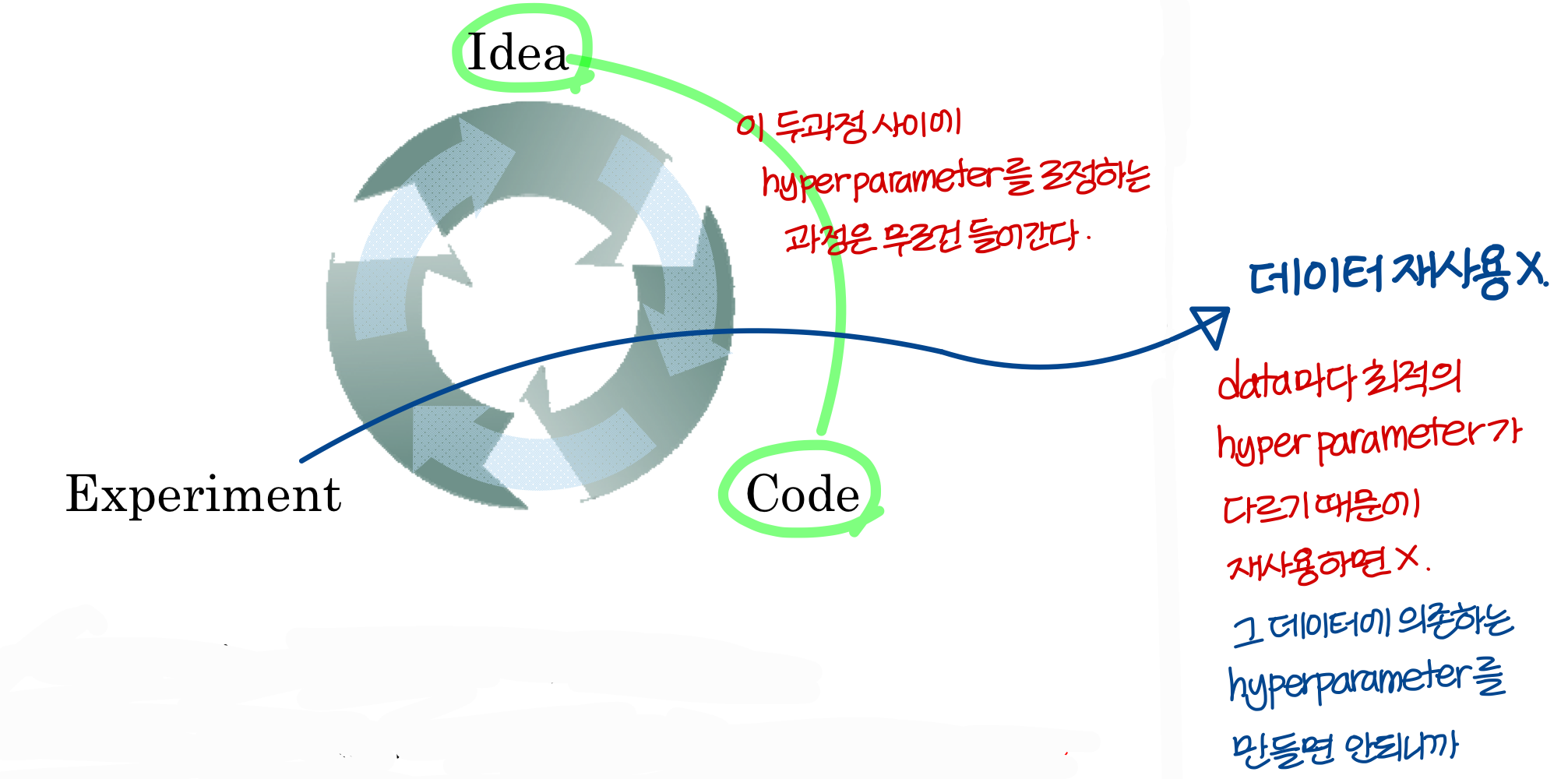
Batch Normalization
- hyper parameter 찾는데 도움을 준다!
- neural network를 hyperparmeter choice에 더 robust하도록 만들어준다
Normalizing inputs to speed up learning
- batch normalization도 Input normalization이랑 완전 비슷하다!
→ 를 normalize 하면? ⇒ 와 를 빠르게 학습시킬 수 있다.
→ input normalize 개념에 layer마다 다르게 하는거 추가했다고 생각하면 된다
→ hidden layer에 대해서 batch normalization을 추가함
→ 가 아니라 에 대해 normalize하는게 맞다!
가 variance가 크기 때문
Implementing Batch Norm
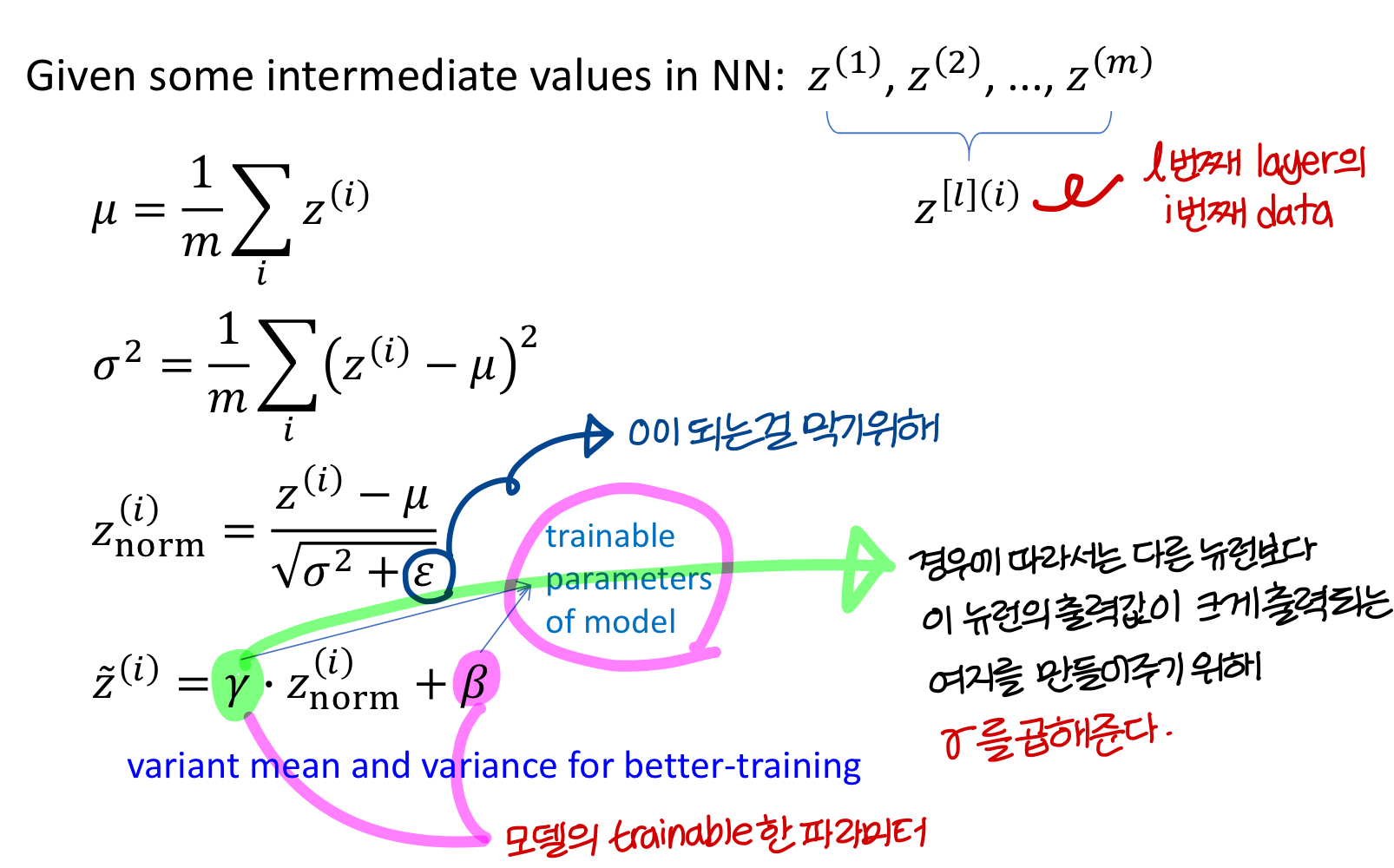

그리고, 감마 값과 베타 값이 다음과 같을 때 →
Adding Batch Norm to network
→ network에 batch normalization을 추가해보자!
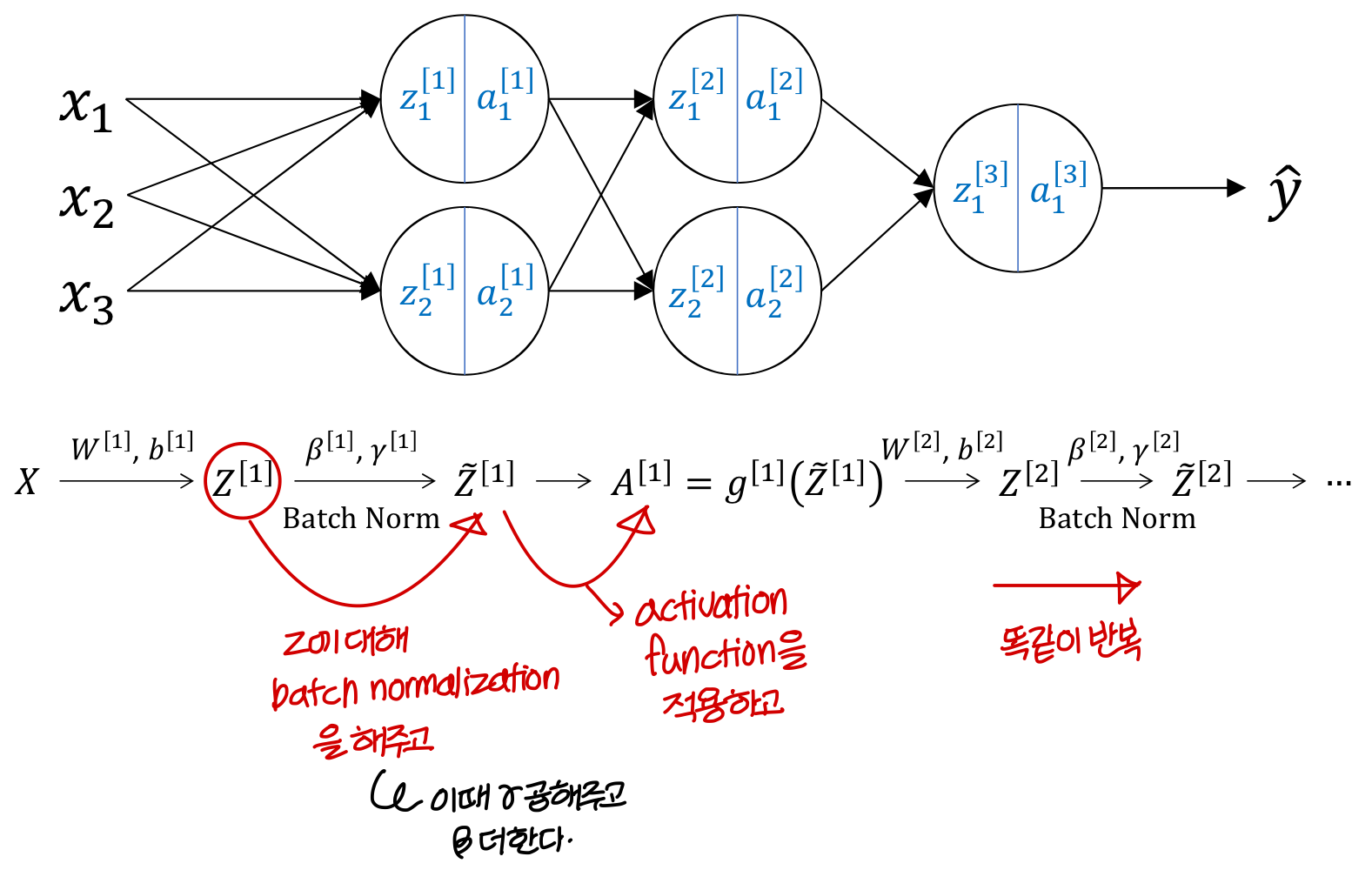
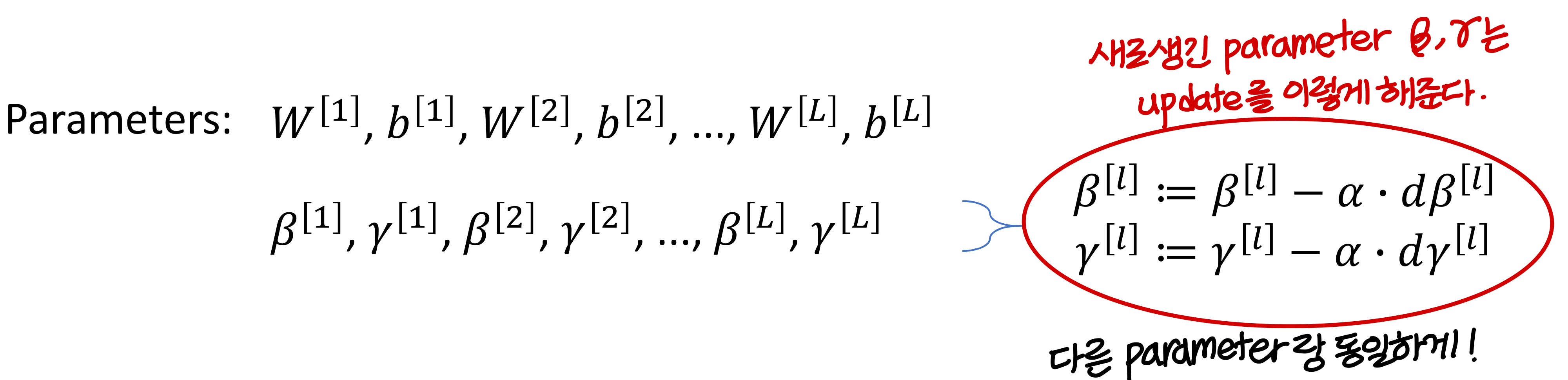
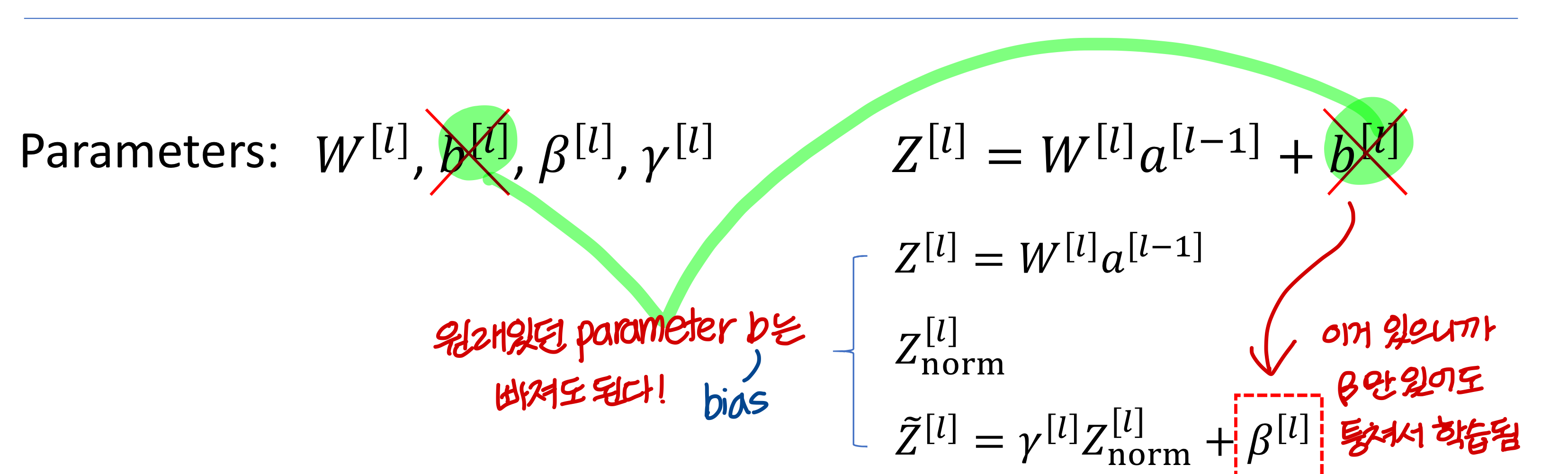
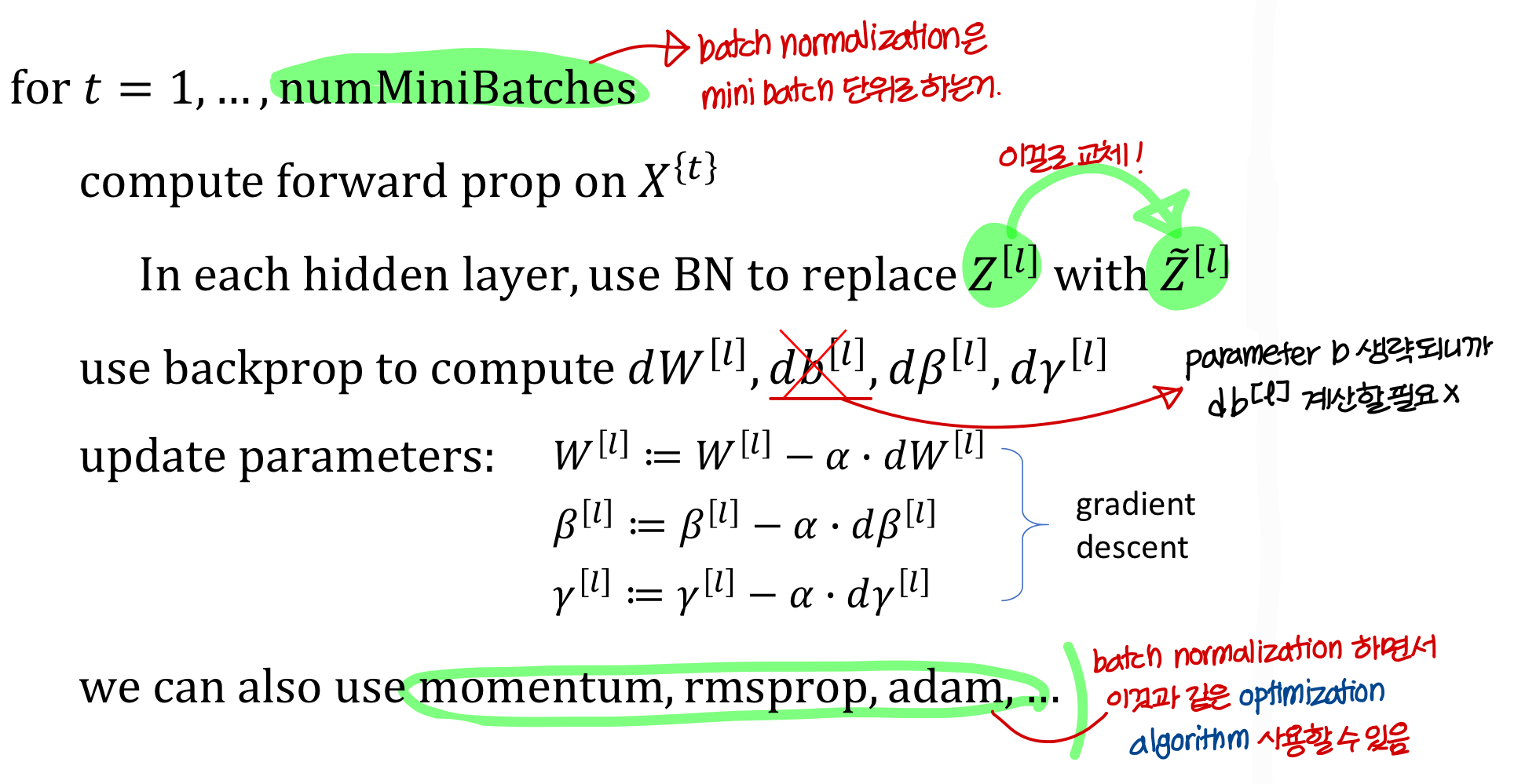
Implementing gradient descent
Learning on shifting input distribution
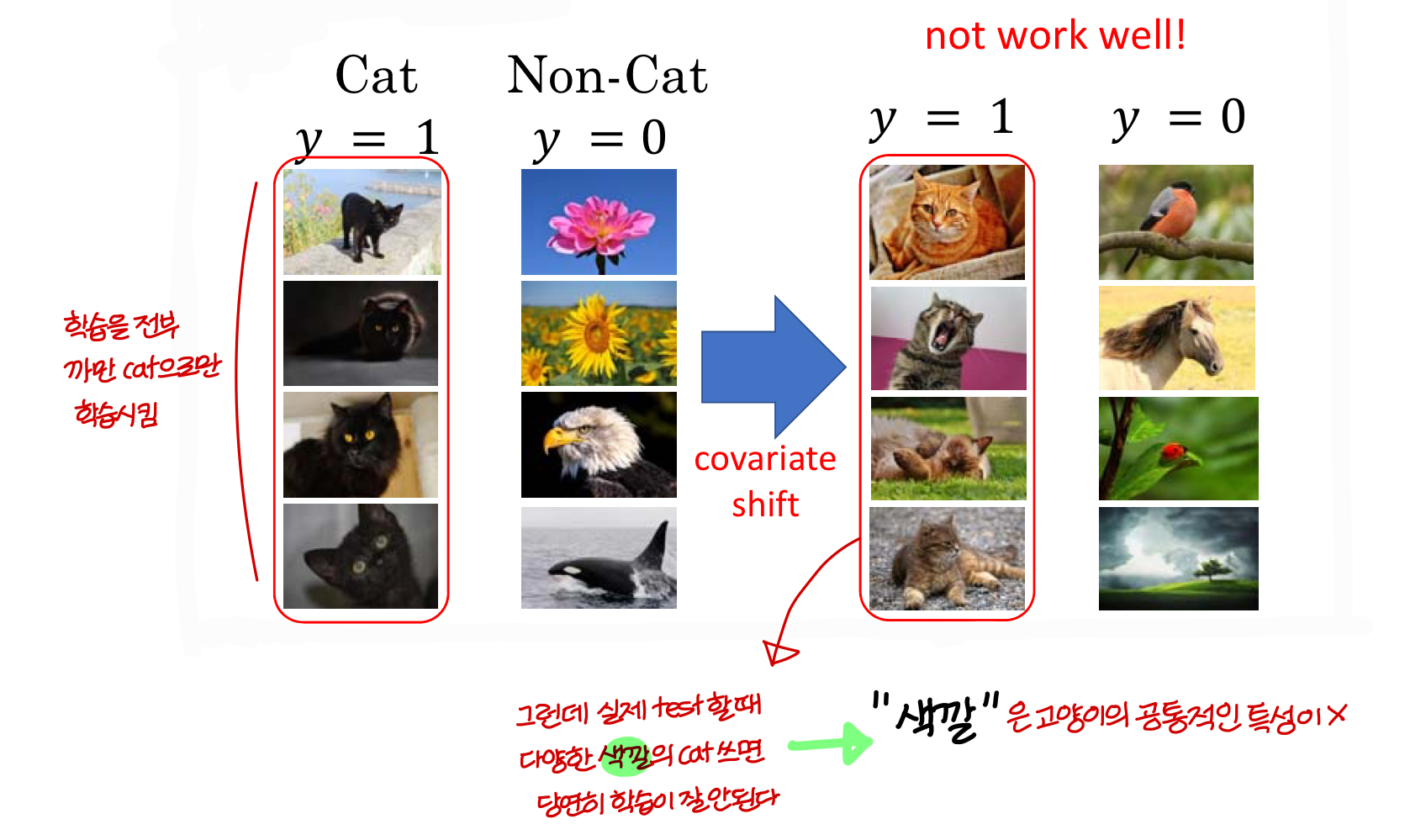
- Cat 집단과 Non-Cat 집단이 공통으로 가지는 feature:
covariate⇒ 이 covariate 때문에 다른 결론이 나왔을 수 있다.
ex) A 수업을 들은 사람 vs B 수업을 들은 사람 ) 성적을 비교하는데
알고보니 두 집단의 나이차가 엄청나다. 이것 때문에 나이 많아서 성적 안좋은건데 수업이 안좋다고 오해할 수 있음
즉, covariate feature는 같게 두고 실험을 해야한다!
- 만약 x 때문에 y가 나오는지 알고싶은데 hidden 변수 h 때문에 결과가 달라졌다면?
→
covariate shift가 발생한거!→
covariate shift: 공변량 변화라고 부르며 입력 데이터의 분포가 학습할 때와 테스트할 때 다르게 나타나는 현상을 말한다.이는 학습 데이터를 이용해 만든 모델이 테스트 데이터셋을 가지고 추론할 때 성능에 영항을 미칠 수 있다.
ex) 위의 경우라면 나이대별로 성적 조사해서 그거랑 얼마나 차이나는지 보정을 하는거지
ex) 고양이를 구분하는 경우라면 까만거에 대한 feature를 covariate shift 해서 다른 feature 강조해야함
Batch Norm as regularization
- Batch normalization을 하면 각 mini-batch는 mean/variance 값만큼 scaled된다.
- 이건 mini-batch의 각 에 noisze를 더하는 거임
→ dropout과 유사하게 각 hidden layers’s actiavation에 noise를 더하는거임
Batch Norm on test(or operation) time
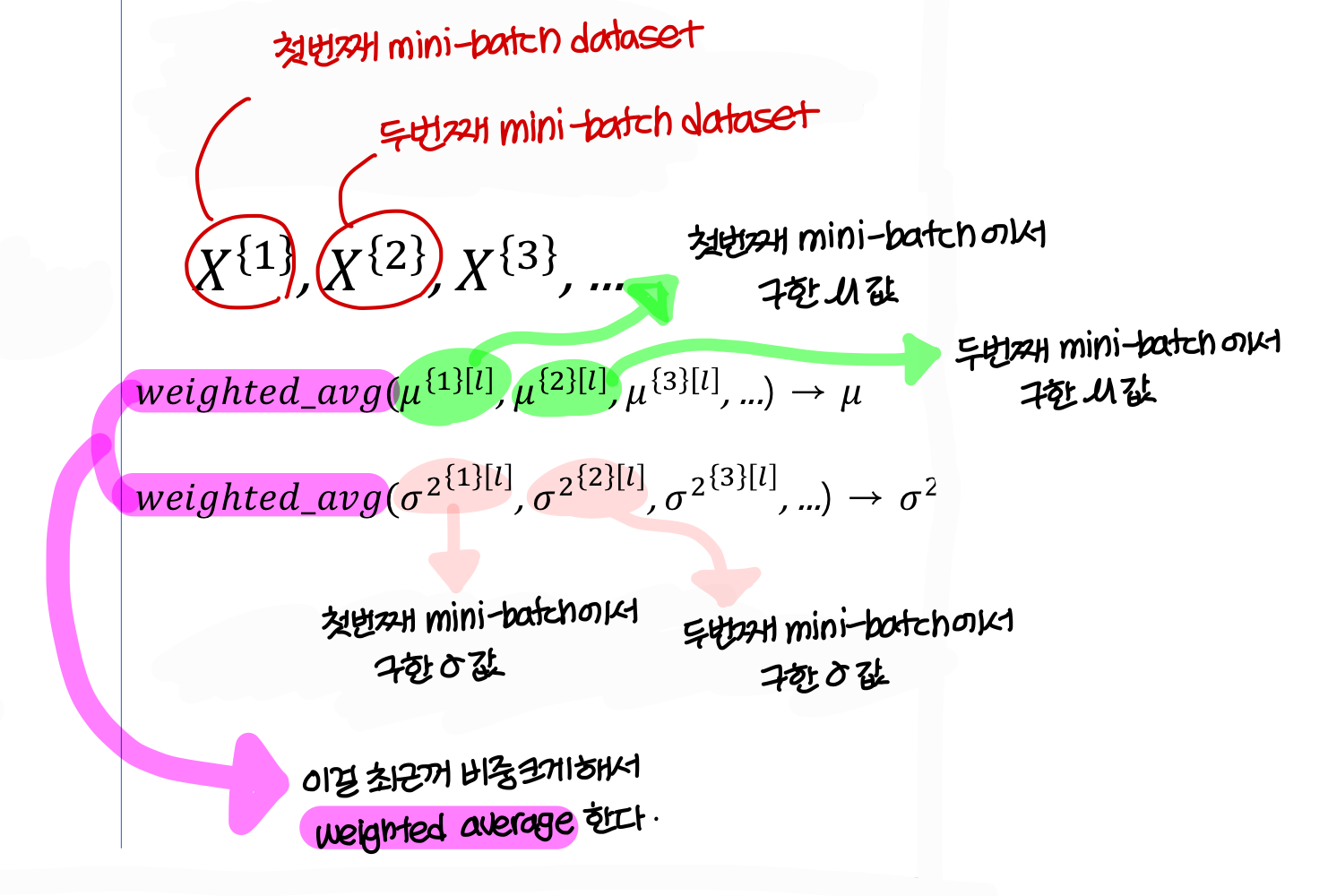
- 앞에선 학습할 때 batch normalization 하는거 본거고,
이제 test time, operation time에 batch normalization 어떻게 하는지 보자!

Uploaded by N2T