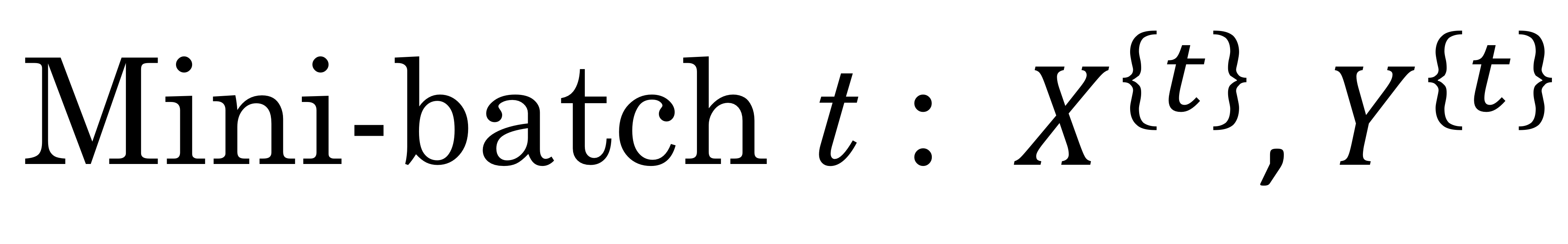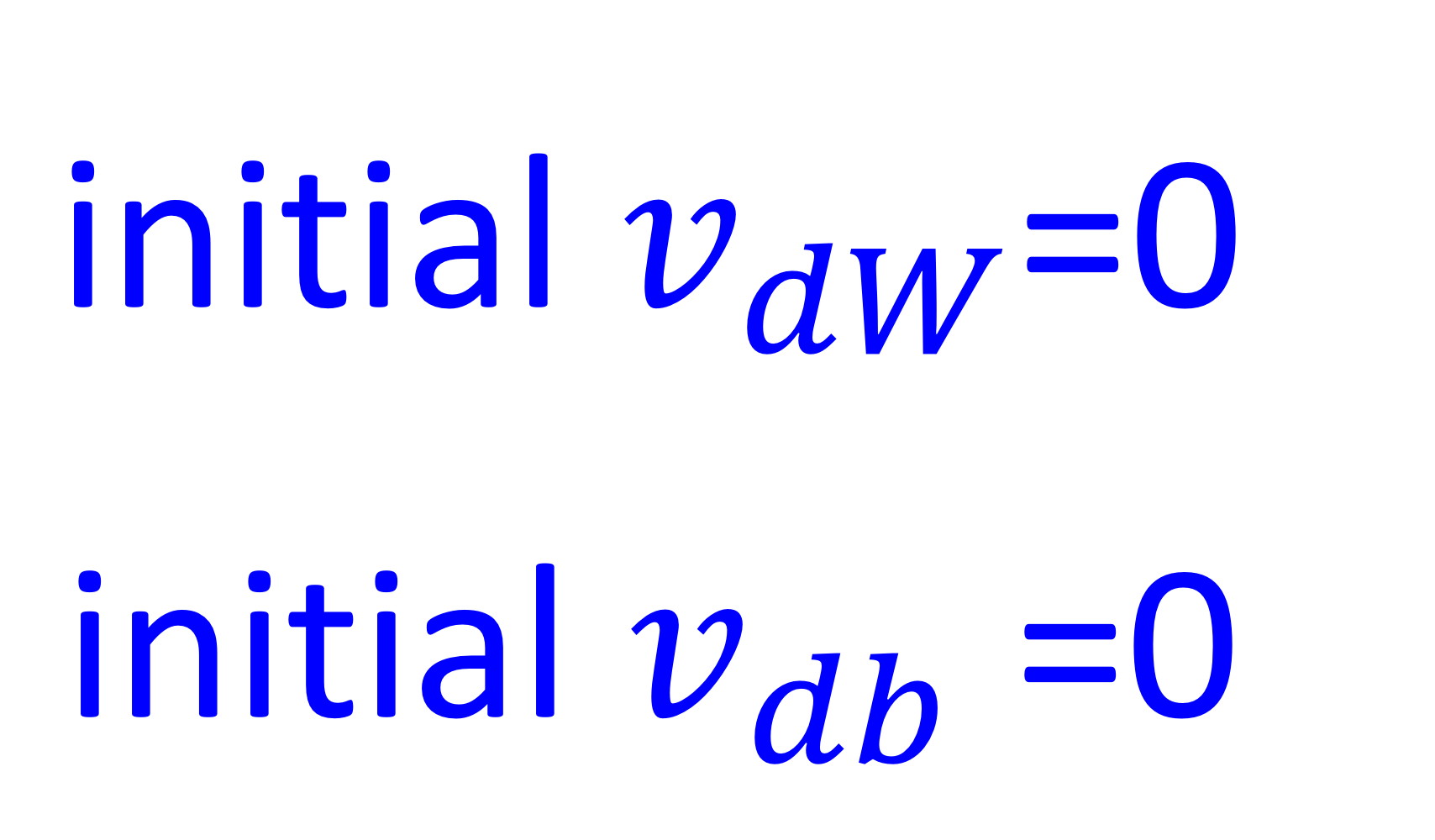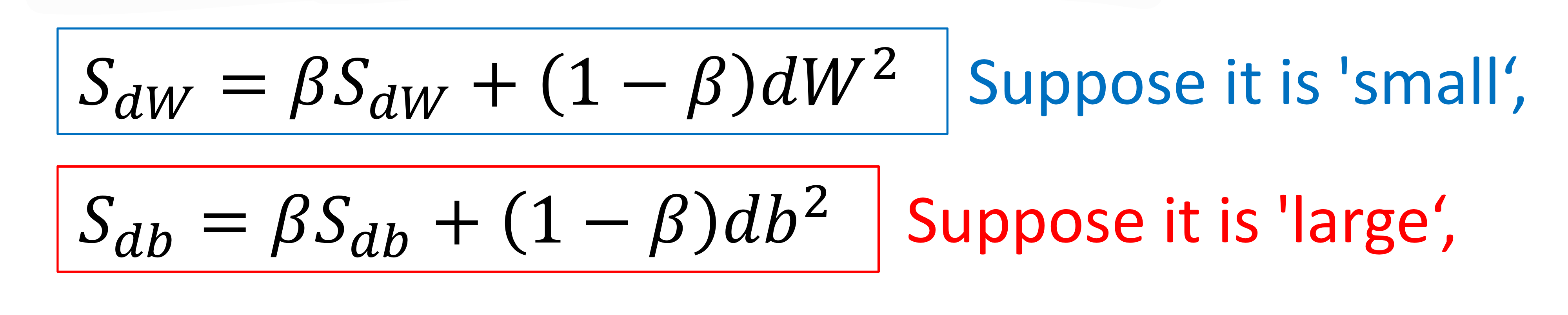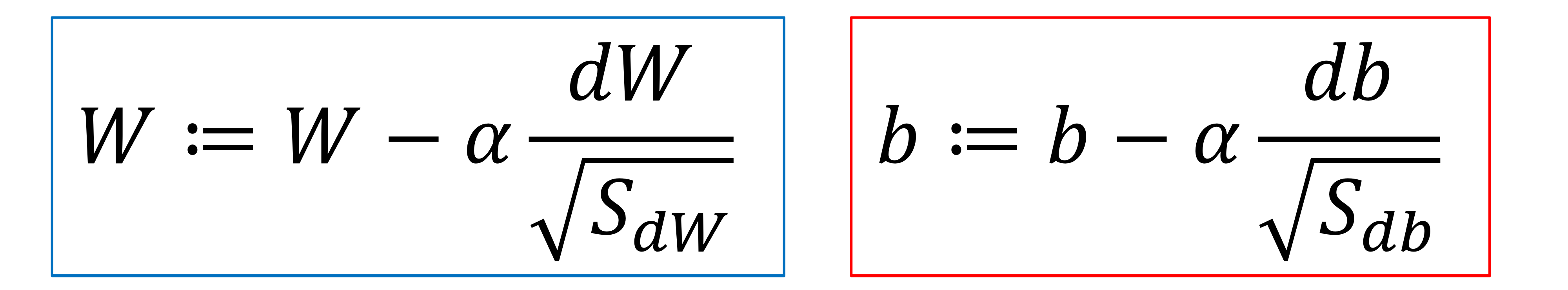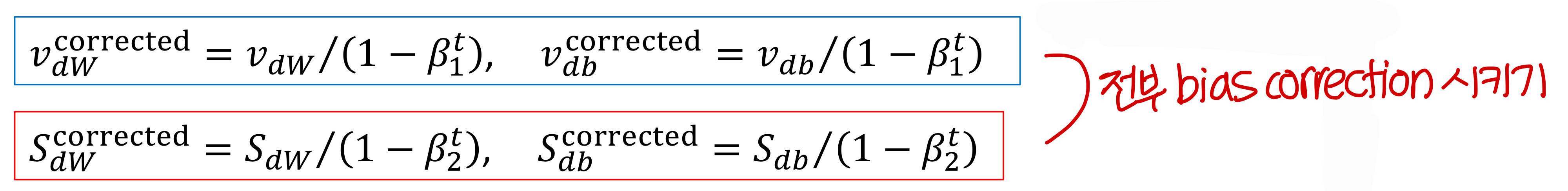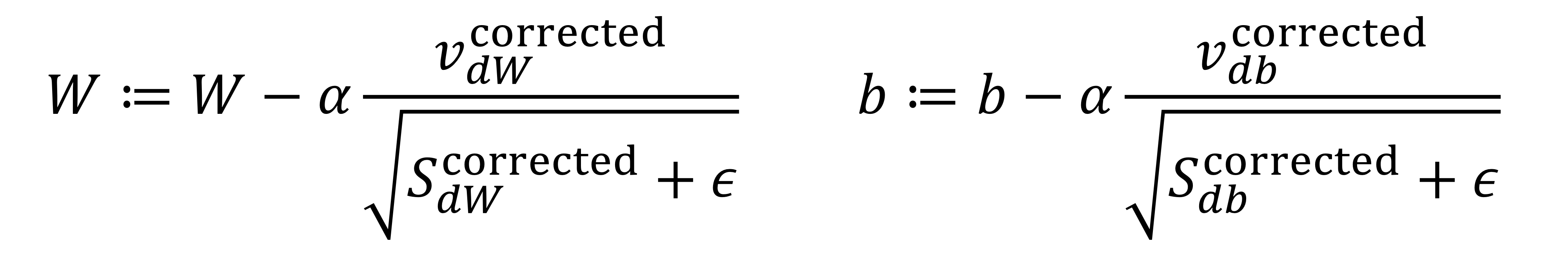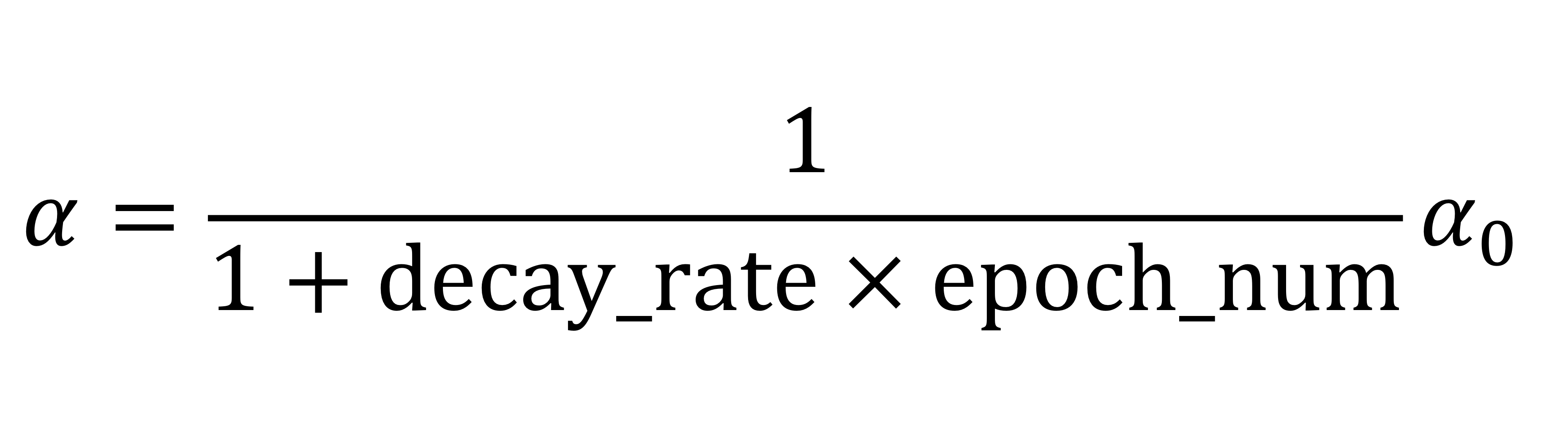- 저번시간에는
effectiveness를 좋게 하기 위한regularization을 배웠음(퀄리티를 좋게 하기 위한 방법)
- 이번 시간에는
efficiency를 좋게 하기 위한optimization algorithm을 배울거임
- machine learning은 highly empirical process임
→ 결과보고 tuning을 하는 과정이 계속 필요함
- deep learning은 big data를 가정하고 하는거!
Batch vs mini-batch gradient descent
- 우리 training data 전체를 하나의 matrix로 만들어서 계산했었음
→ 근데 이 방법은 training data가 너무 많을 때 한계가 있다!
→ 한 번에 다 합해서 gradeint 계산하면 너무 오래 걸림
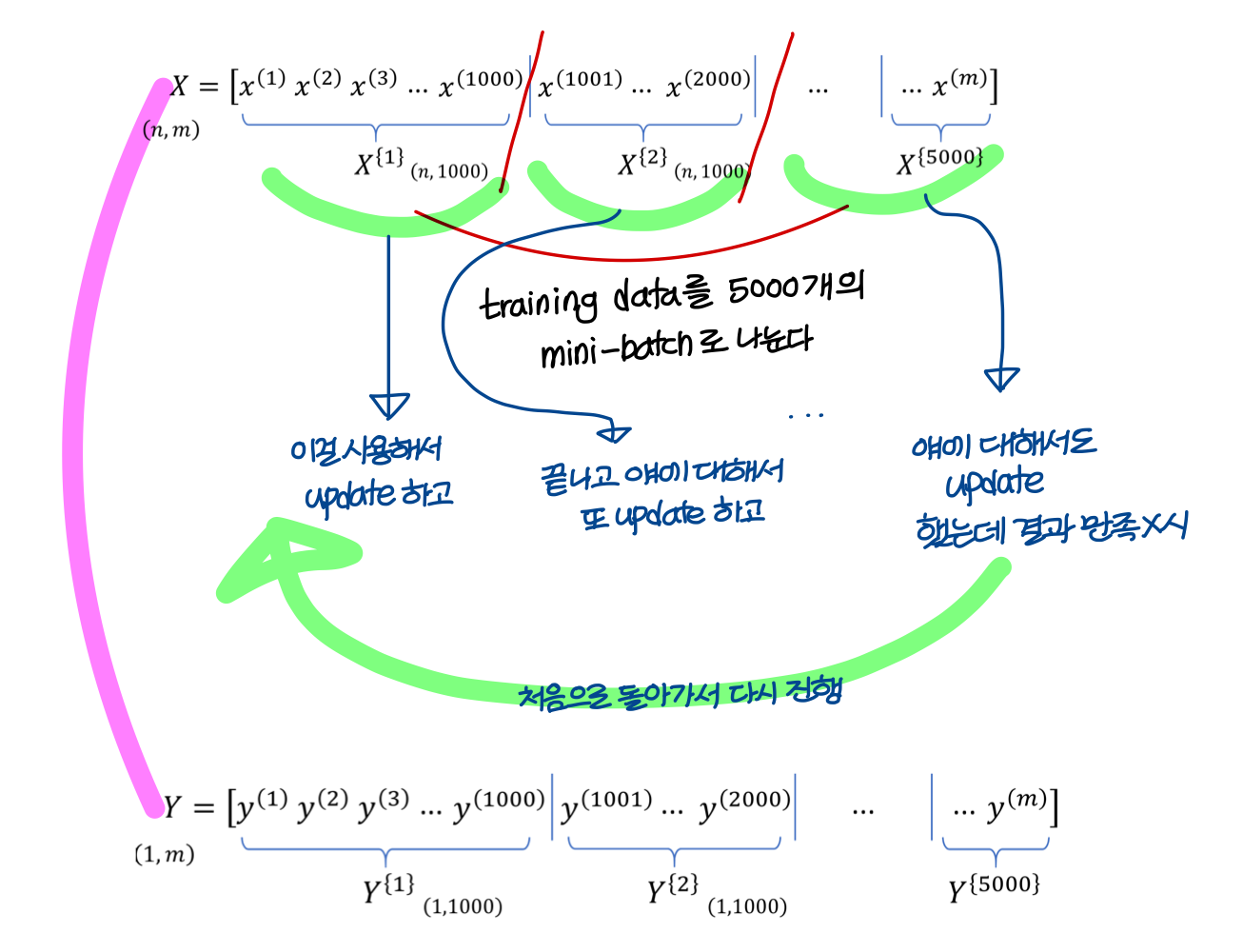
- 즉, training data 전체는
batch, 작게작게 자른거 하나하나를mini-batch라고 함
- mini-batch 하나를 도는걸 한
iteration이라고 표현함
- 전체 training data 다 돈걸(batch 다 돈걸)
epoch라고 표현함
Training with mini-batch gradient descent
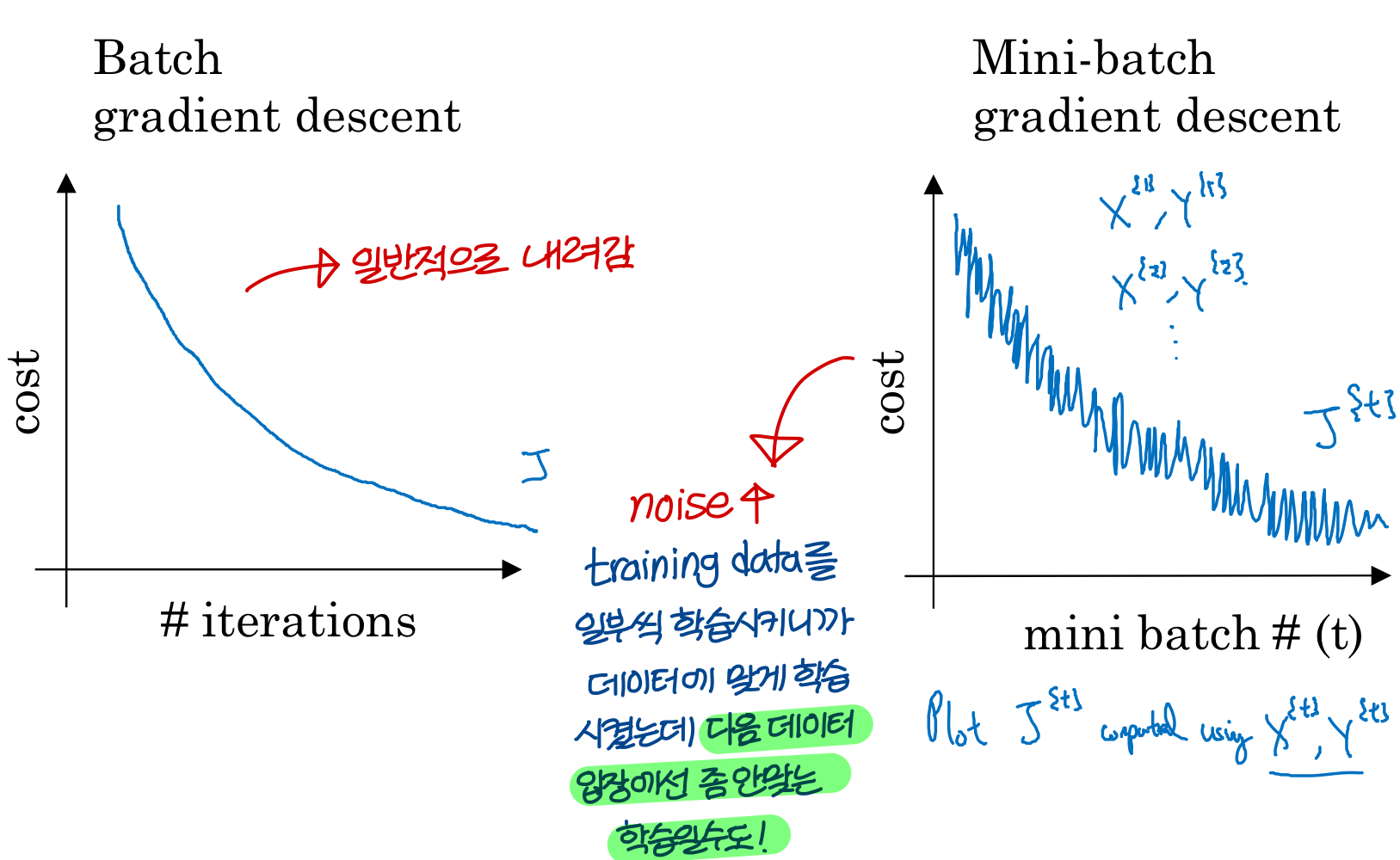
Choosing your mini-batch size
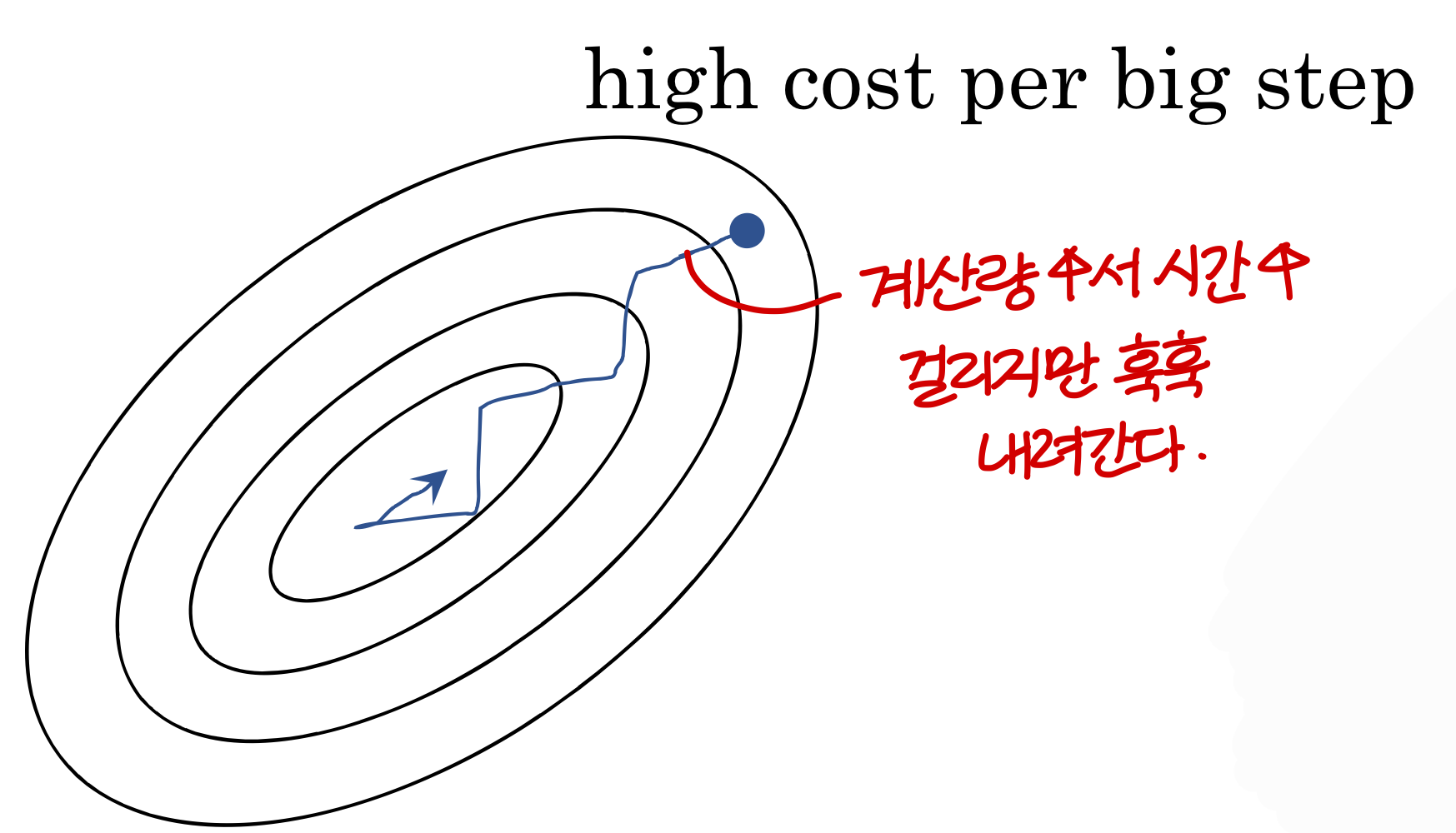
→ 한 iteration(=epoch)당 너무 오래걸린다!!
- 만약 mini-batch size가 1이라면 → training data 하나하나가 mini-batch임
→ vectorization(=parallelization)으로 얻을 수 있는 speedup을 이용할 수 X
- 만약 training data set의 크기가 2000보다 작으면
batch gradient descent를 해라! (= 한꺼번에 돌려라!)
- 아니라면 mini-batch 사이즈 기준으로 잡아야함
메모리 자체가 기준으로 설계되어 있으니까
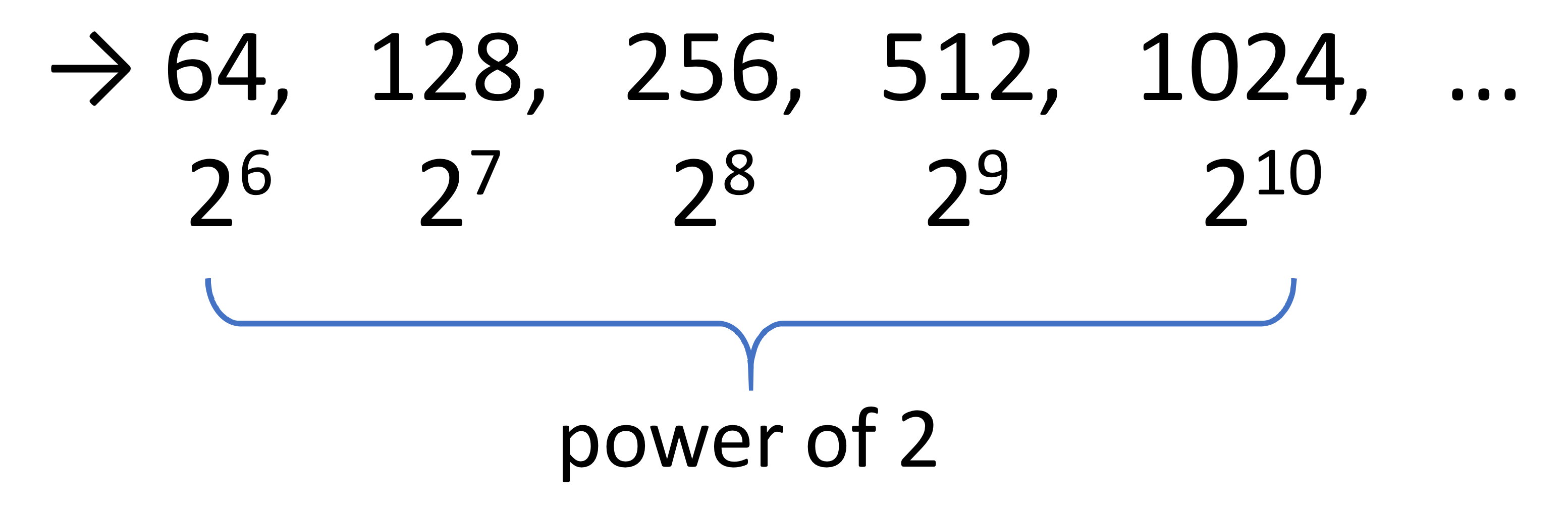
⇒ 이렇게 하면 mini-batch가 CPU/GPU memory에 fit되게 할 수 있다!
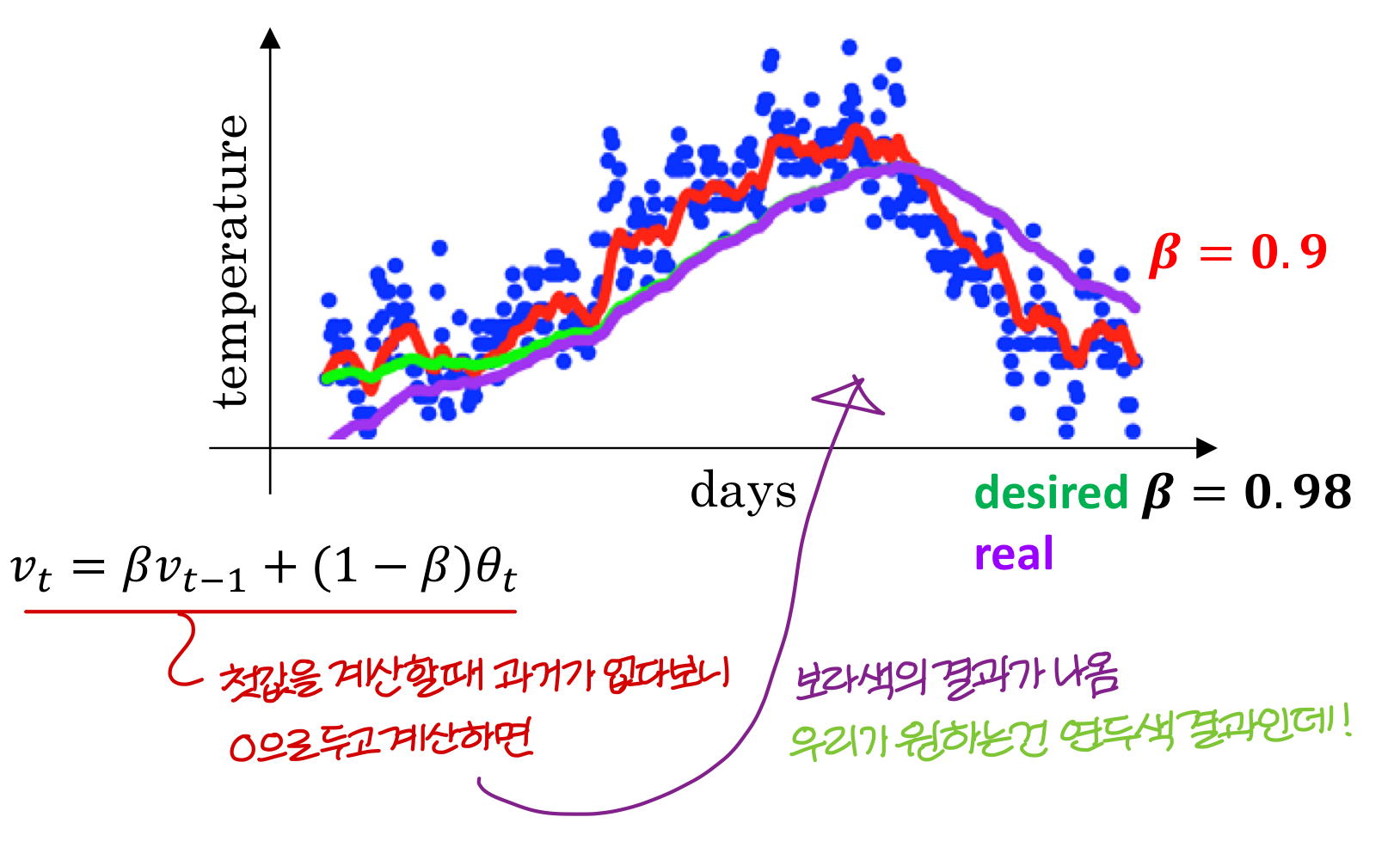
Exponentially weighted averages for understanding momentum(관성)
→ avg() 이런식으로 하면 과거 정보 들고 갈 수 있음
→ 근데 과거 정보를 얼마나 average 해야 할까?
현재 꺼가 더 중요한데 과거 정보 너무 많이 사용하는 것도 문제임
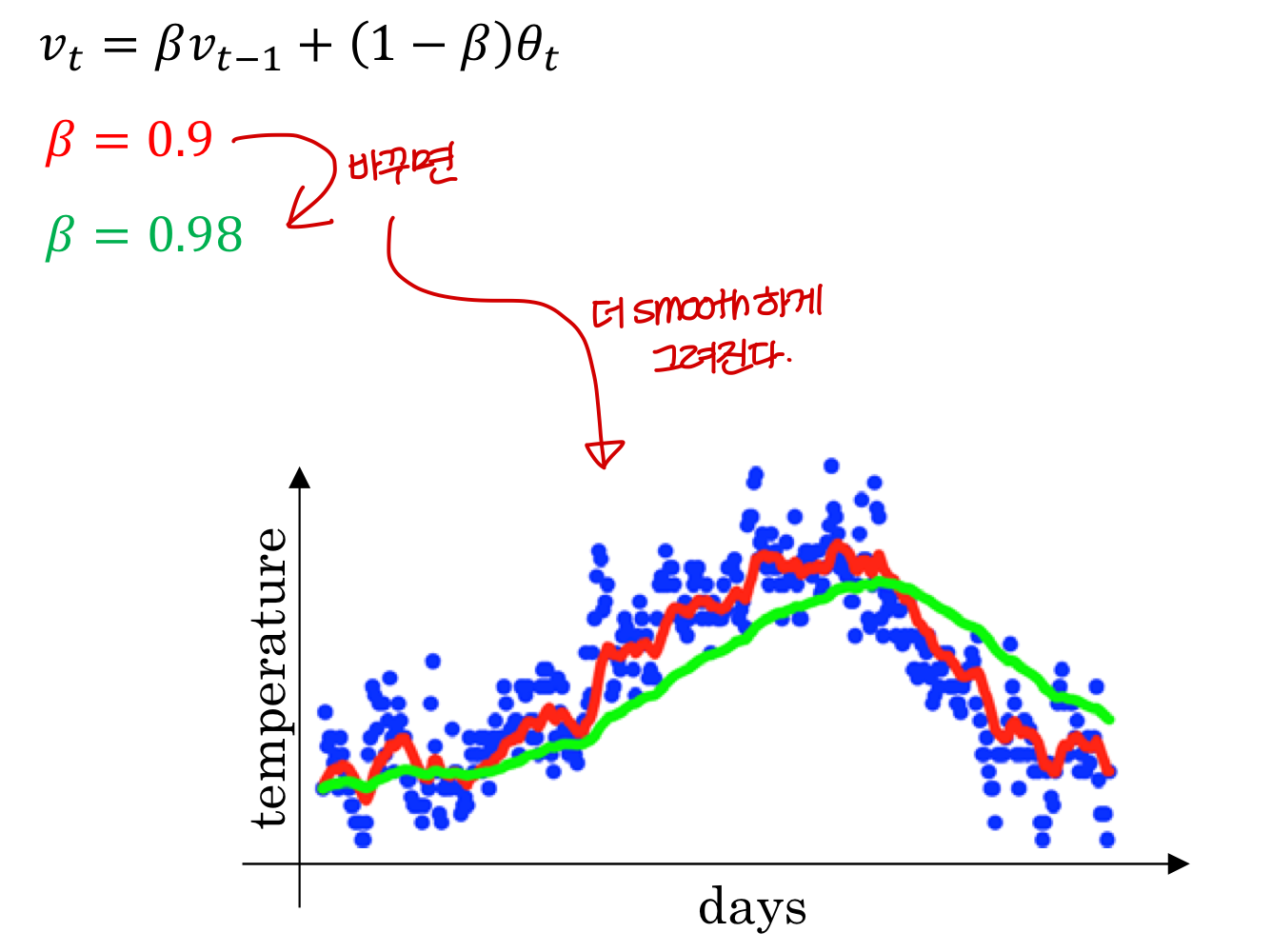
그래서 최신꺼를 더 많이 반영하기 위해 단순 average를 쓰는게 아니라, exponential weighted average를 사용한다!
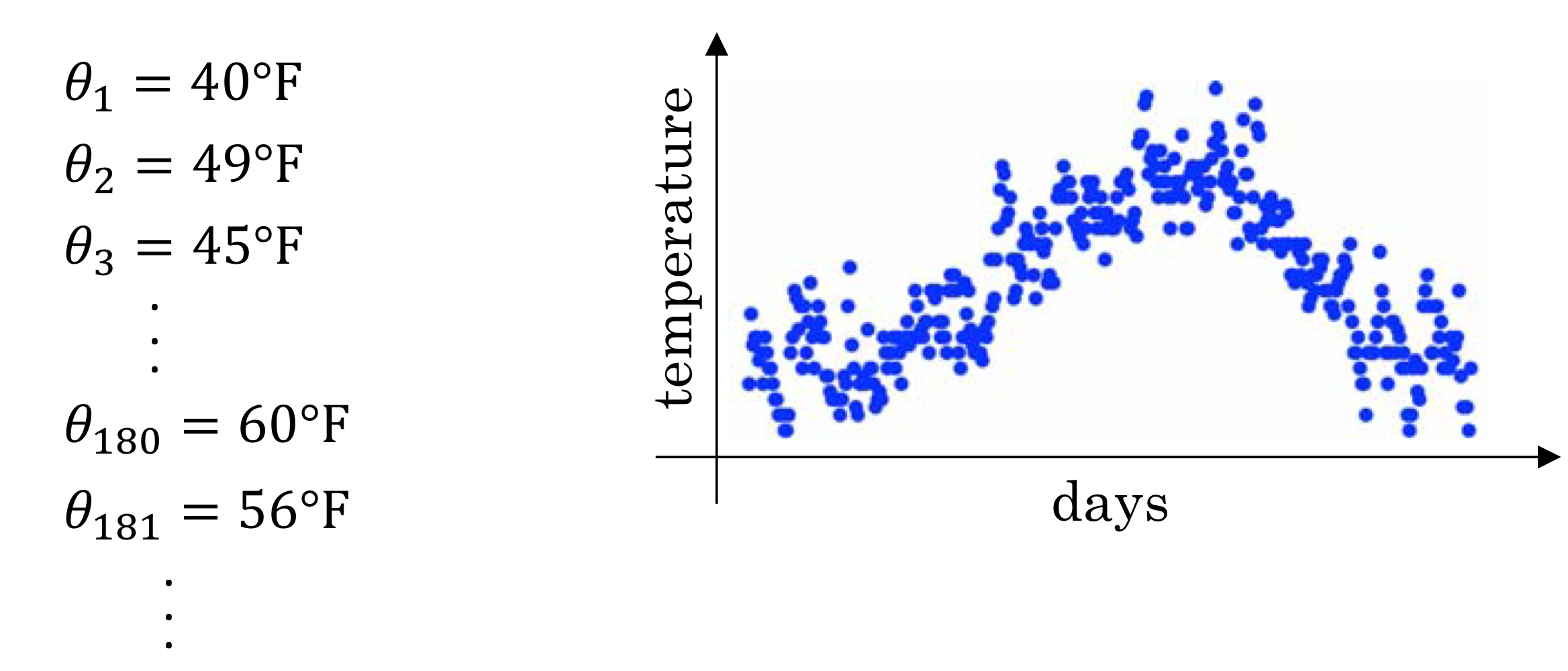
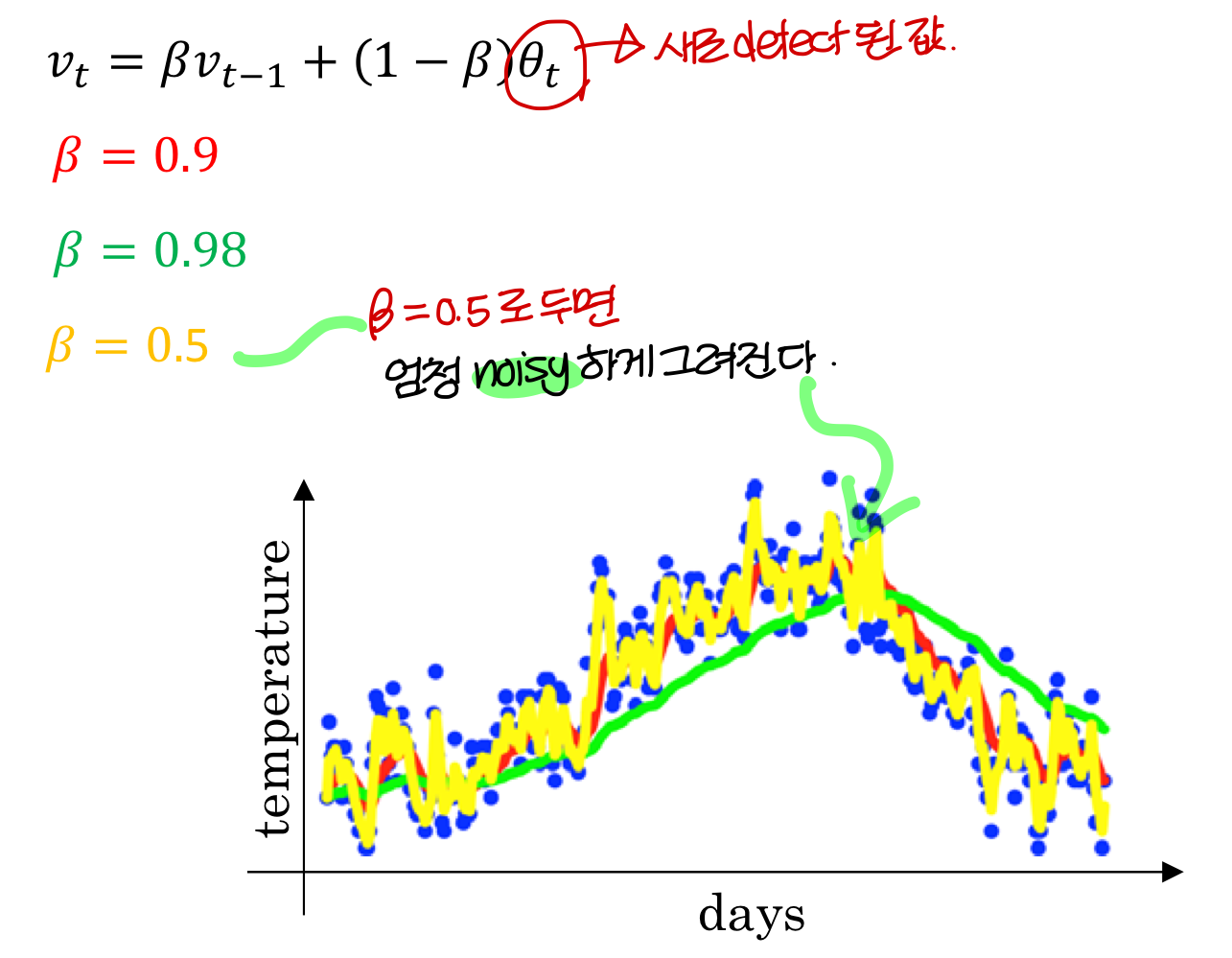
Temperature in London
가중치 0.9
가중치 0.98
가중치 0.5
Exponentially weighted averages
- 결과적으로 이런 수식이 된다!
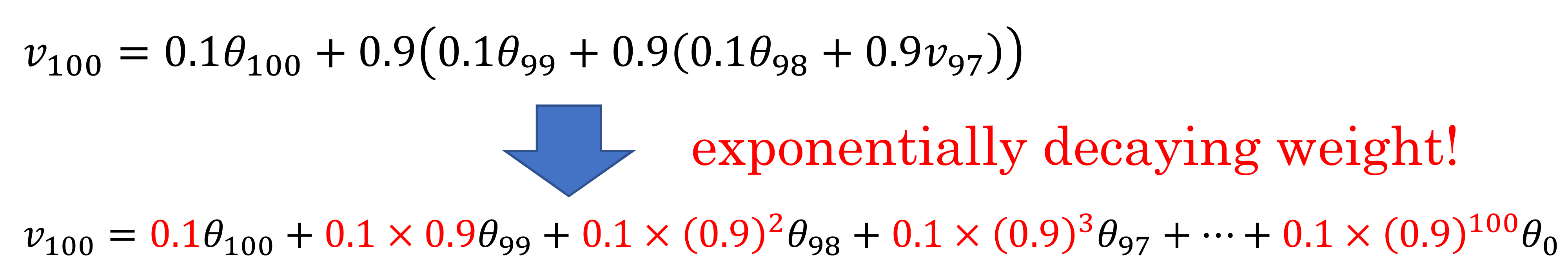
- 일반화해서 을 전개해보면
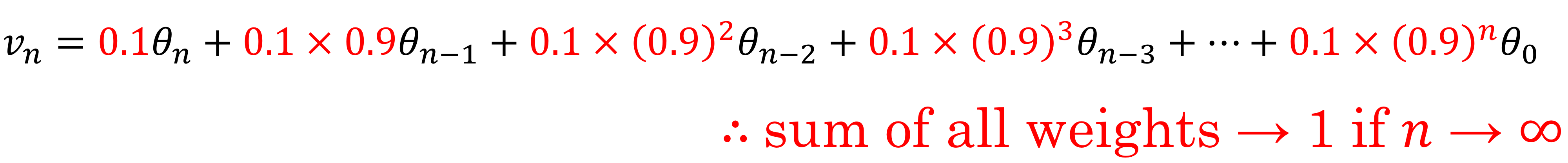
Implementing exponentially weighted averages

Bias correction
⇒ bias correction 하기 전엔 진정한 average가 아님!
⇒ bias correction으로 진정한 average를 만들 수 있음

이걸로 나눠주면 교정되는 이유가 뭘까? 전개해서 알아보자!

Optimization algorithms
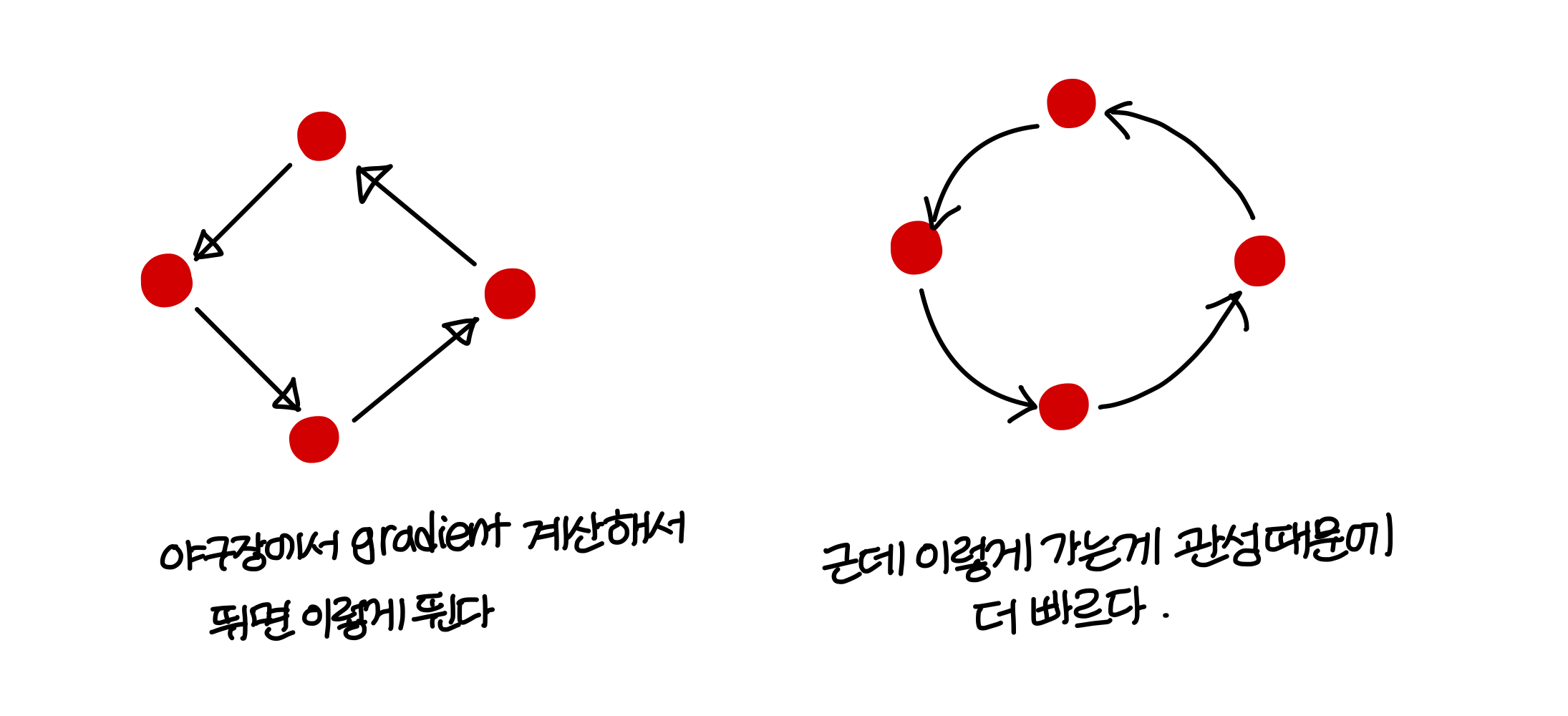
Gradient descent with momentum→ 우리가 앞에서 배운거
→ exponentially weighted average of gradients를 사용
→ 근데 초반값에 bias가 많아서 bias correction으로 해결할 수 있음
RMSPRop
ADAM→ 이건 momentum이랑 RMSProp 더한거
→ 오픈소스에서서 제일 많이 사용하는 방법!
Gradient descent example
mini batch X, momentum X
mini batch O, momentum O

→ initial gradient가 틀리는게 찝찝하면 써야지 (학습을 짧게 시킨다면 써야할듯?)
→ initial value 이렇게 써도 된다
→ 여기서 hyper parameter는 와
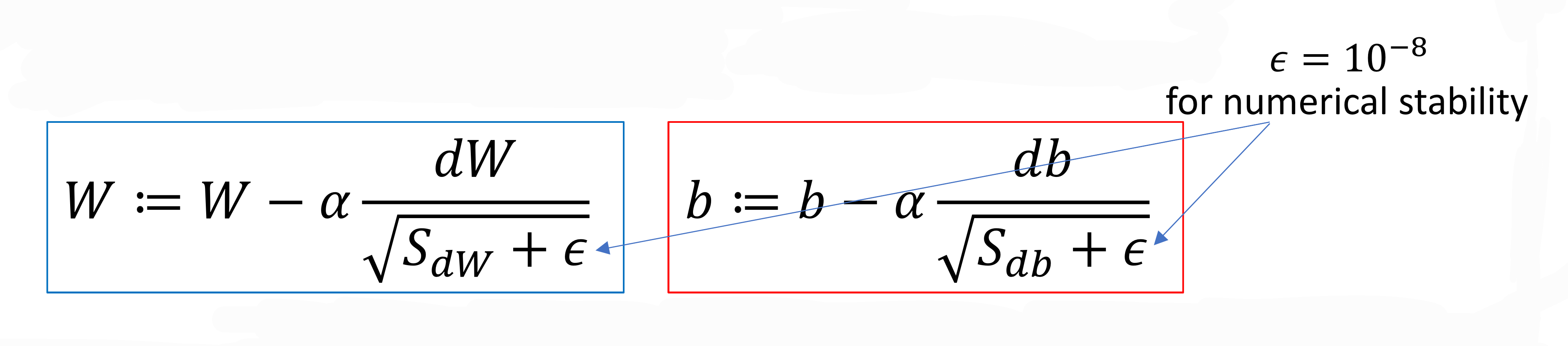
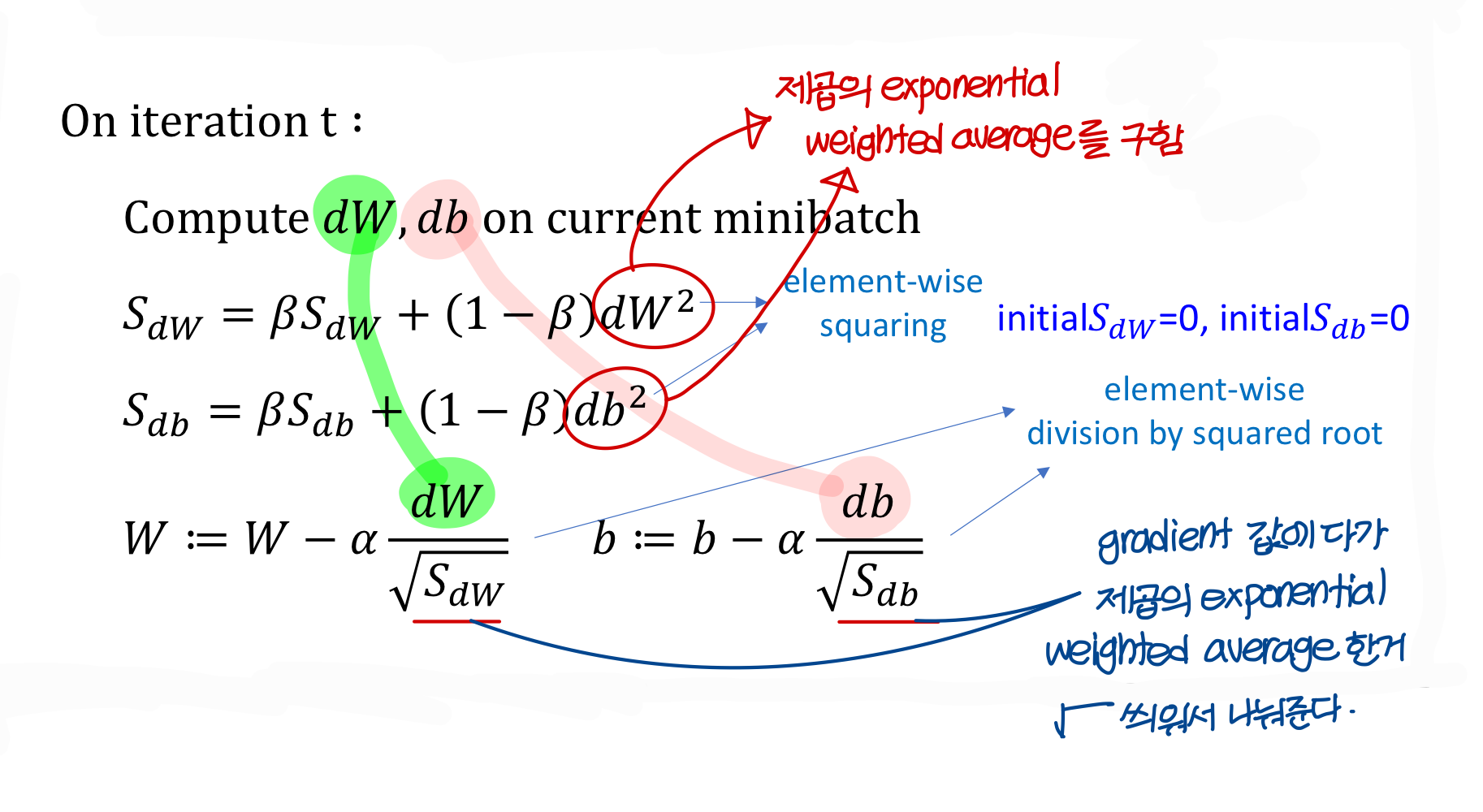
RMSProp: root mean square propagation
- gradient descent 과정에서 oscillation이 생기는 문제가 발생할 수 있음
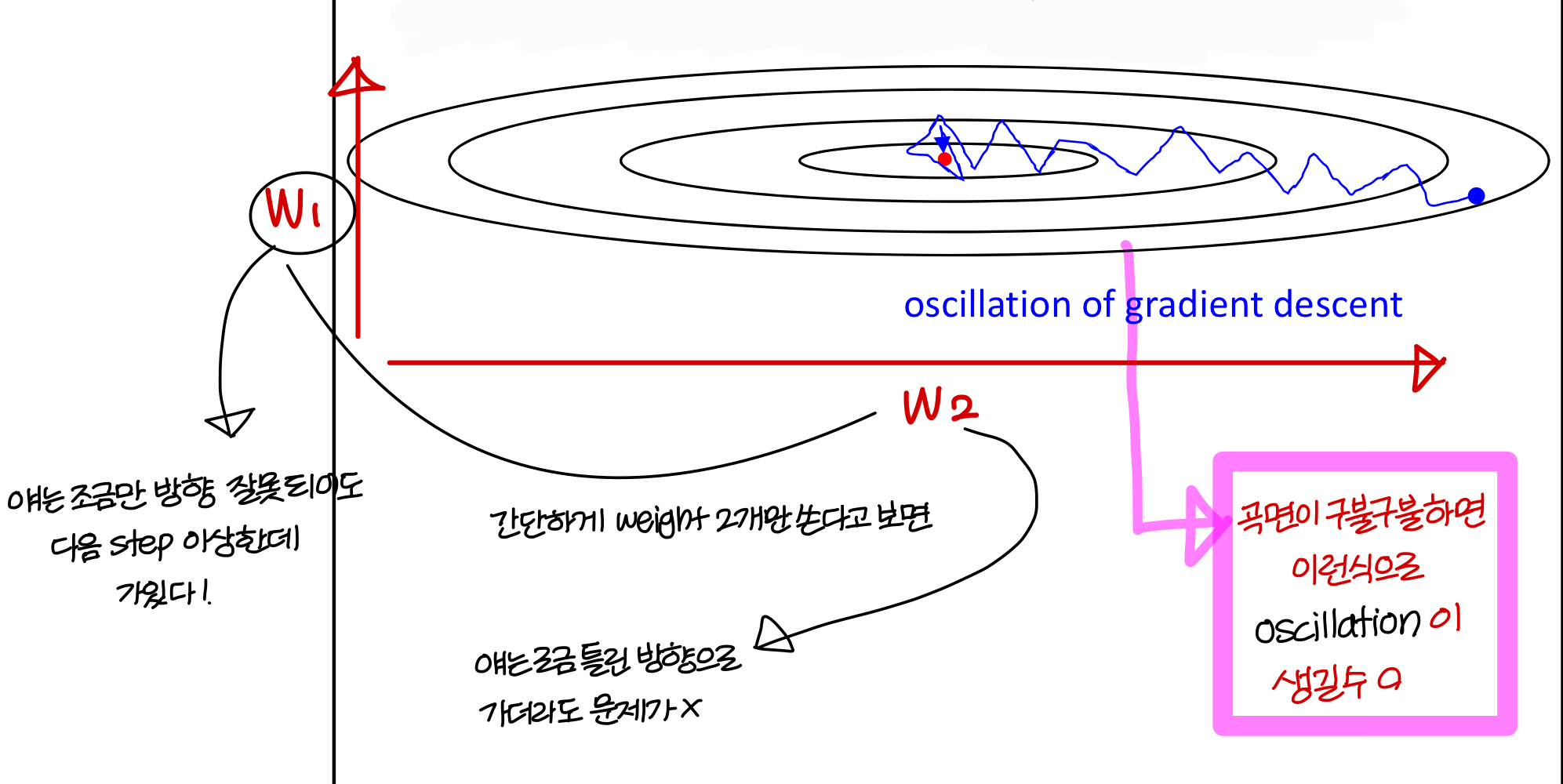
- 제곱의 exponential weighted average 구해서 gradient에 루트 씌워서 나눠줌
Adam optimization algorithm
- momentum이랑 RMSProp보다 이걸 더 많이 씀
→ 왜냐면 Adam이 momentum이랑 RMSProp 통합된 버전임
→ parameter 조정하면 하나씩 쓰는 것도 가능
Adam 사용하는 방법
Hyperparameters choice
- hyperparameters는 이렇게 고르면 된다!
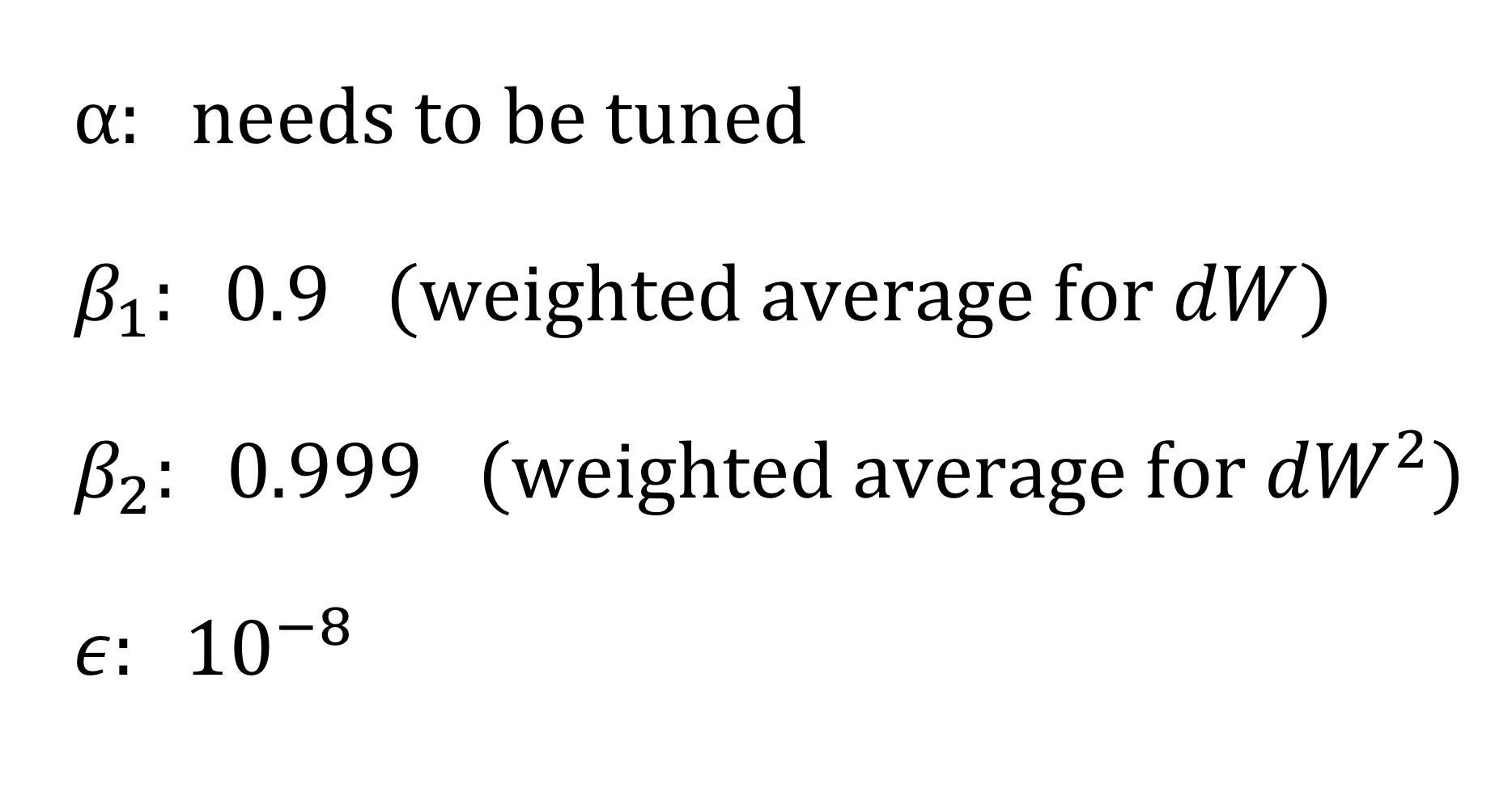
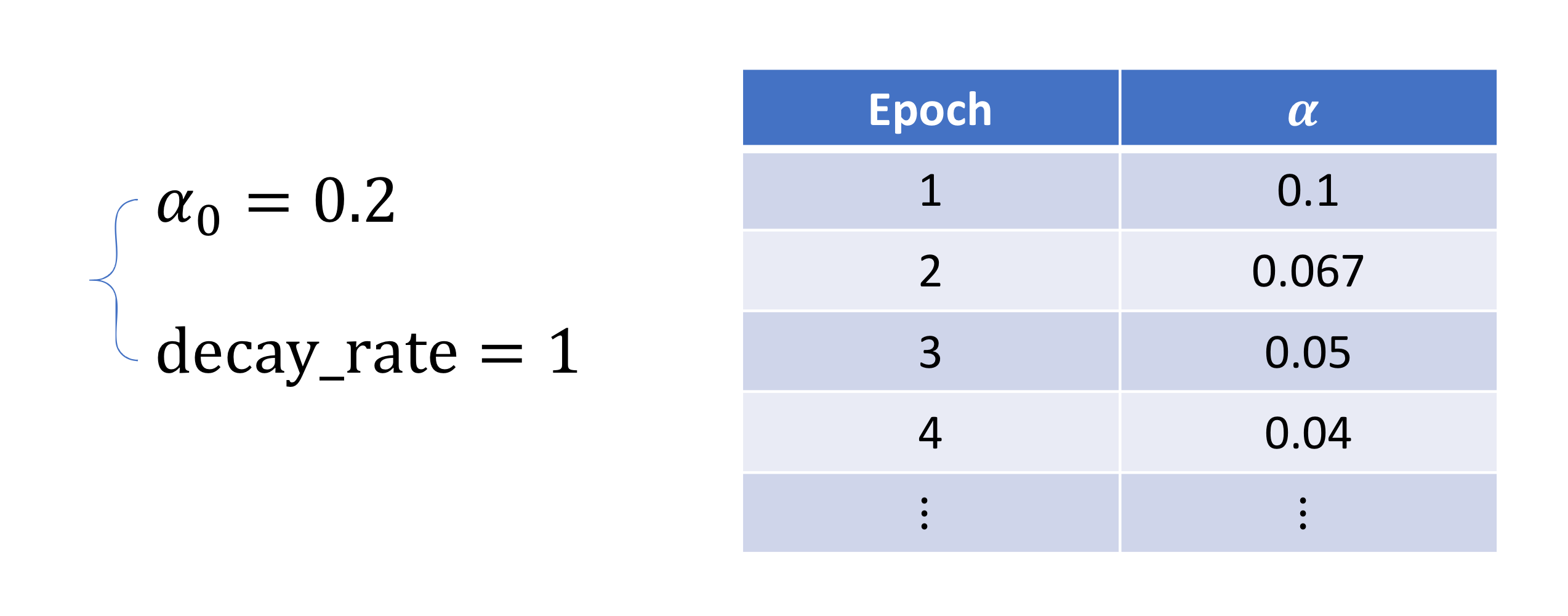
Learning rate decay
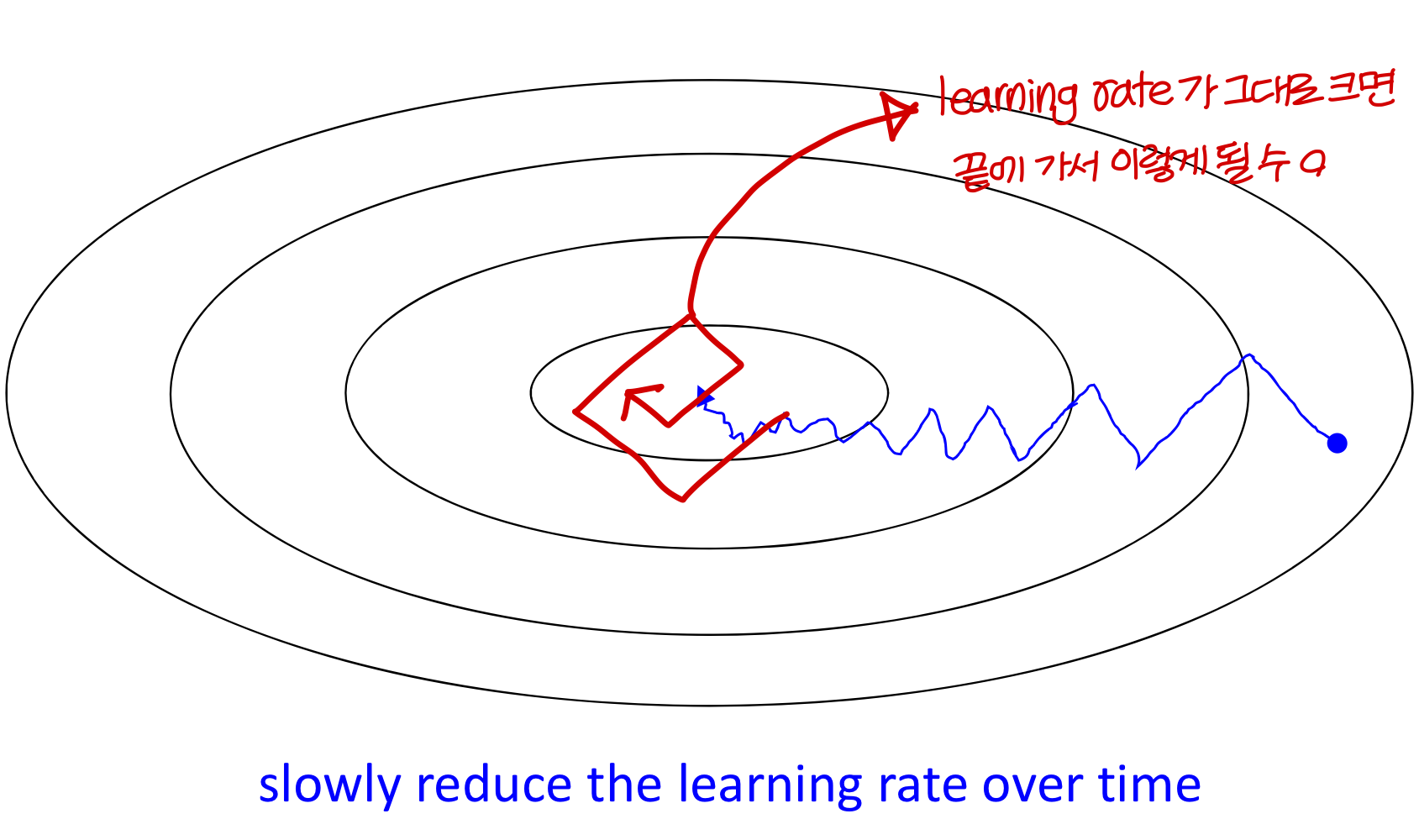
Implementing learning rate decay
- 용어 정의 정확히하기!
step: 데이터 하나에 대해서 한번 돈거
iteration: mini_batch 하나에 대해서 한번 돈거
→ 뒤에서 다른 방법도 배운다!
Other learning rate decay methods
뭐 이런 다양한 방법이 있다

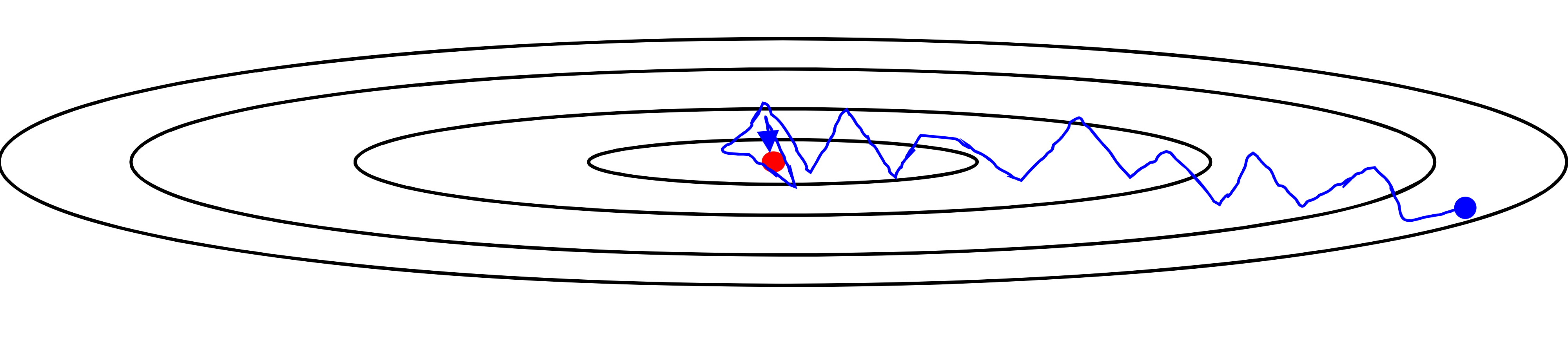
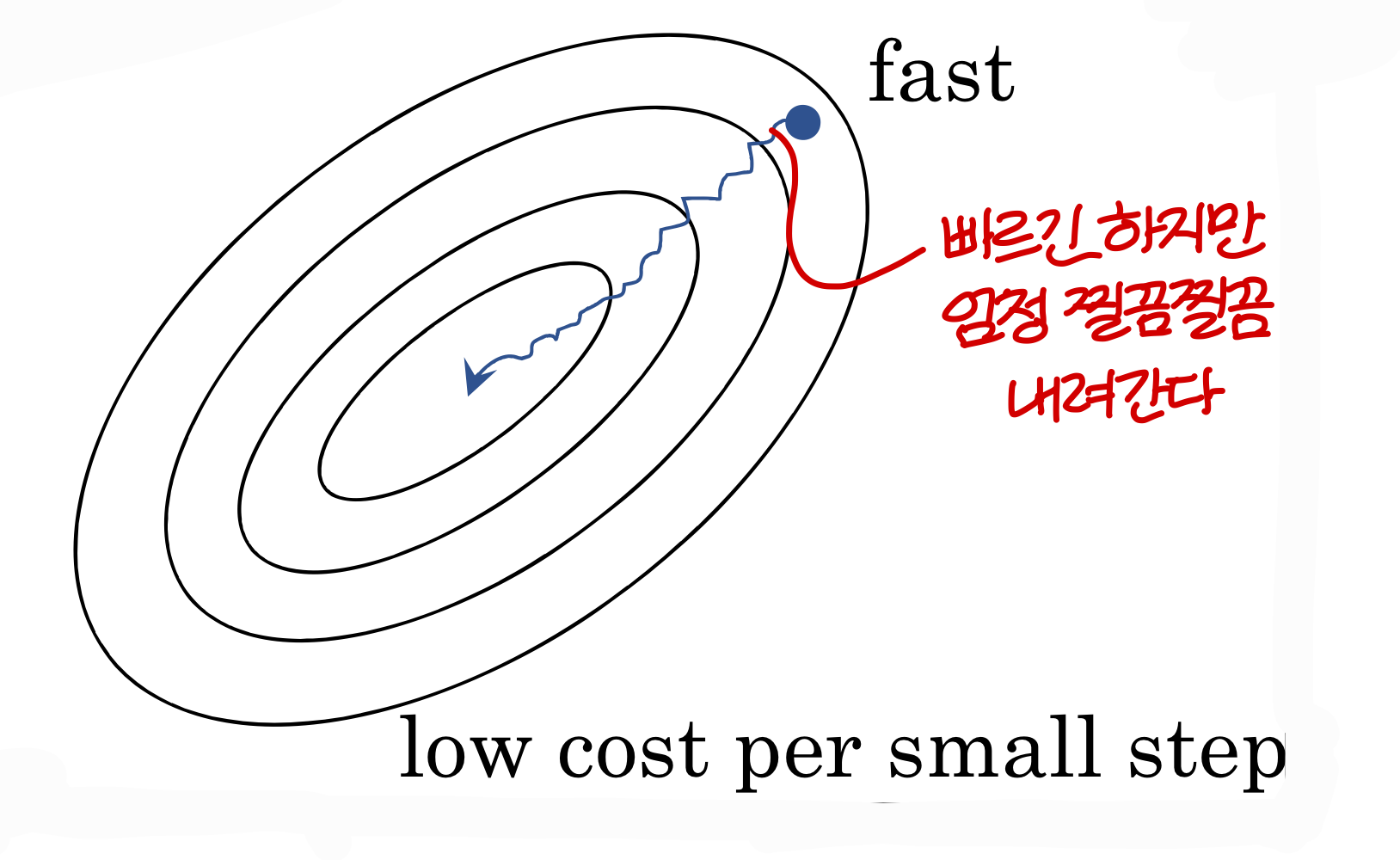
Local optima in neural network
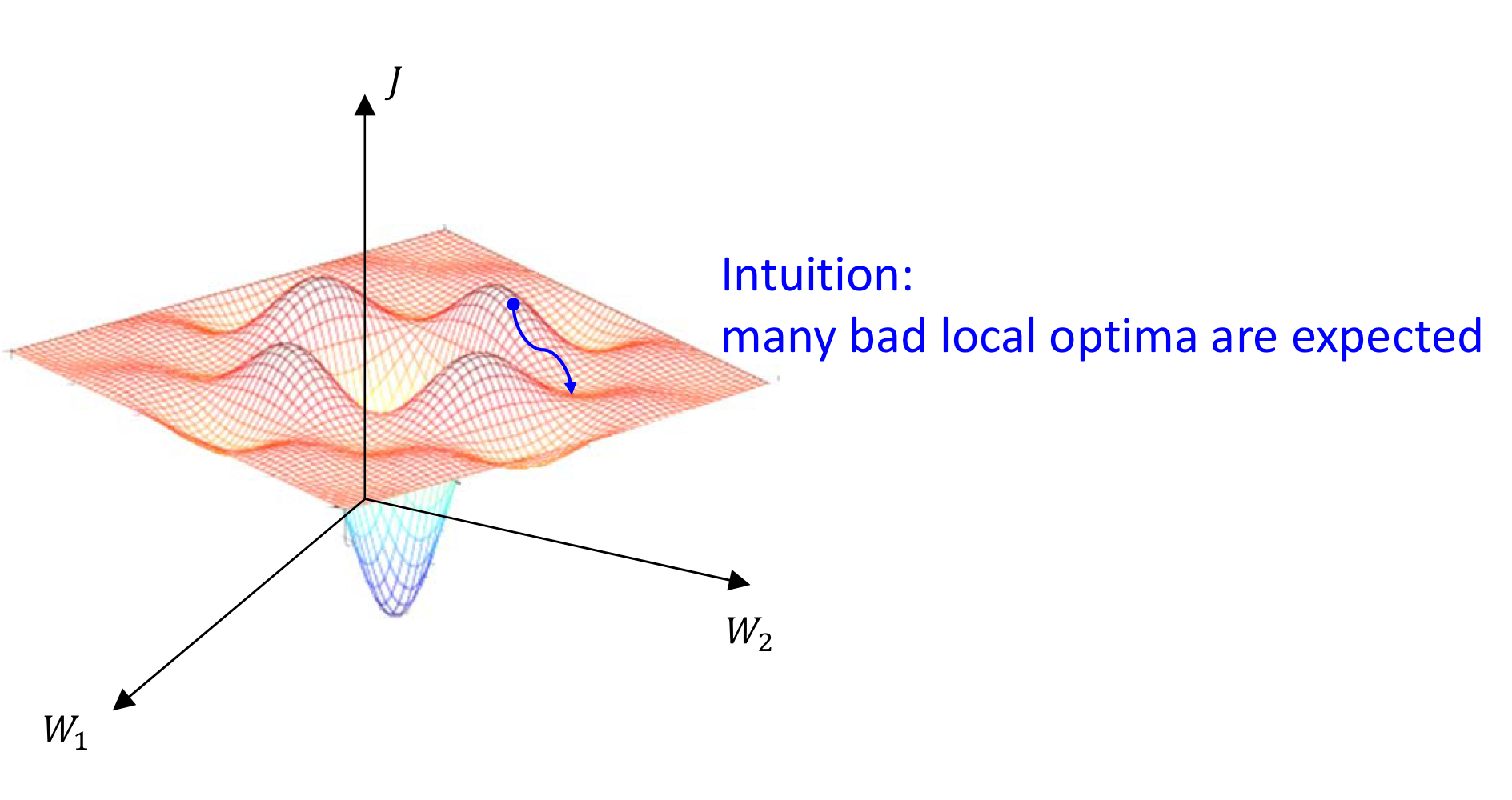
→ 아직 최종목표(global optima)에 도달하지 않았음에도 불구하고,
어느 지점에 도달하면 어느 방향으로 진행하더라도 cost가 증가하다보니 수렴으로 간주하는 문제
→ 근데 사실 이거 걱정할 필요 없다는걸 수학자가가 증명함
그 수많은 w가 모두 local optima에 빠져야 w 업데이트가가 정지되기 때문.
⇒ 그럴 가능성은 매우 희박
⇒ 모든 차원에 대해 다 미분했을 때 양수여야함 (그럴 가능성은 희박. 하나는 음수겠지)
→ 실제로는 이런 local optima는 거의 존재 X
Problem of plateaus
→ 이건 Local optima와 다르게 진짜 걱정할만한 문제!
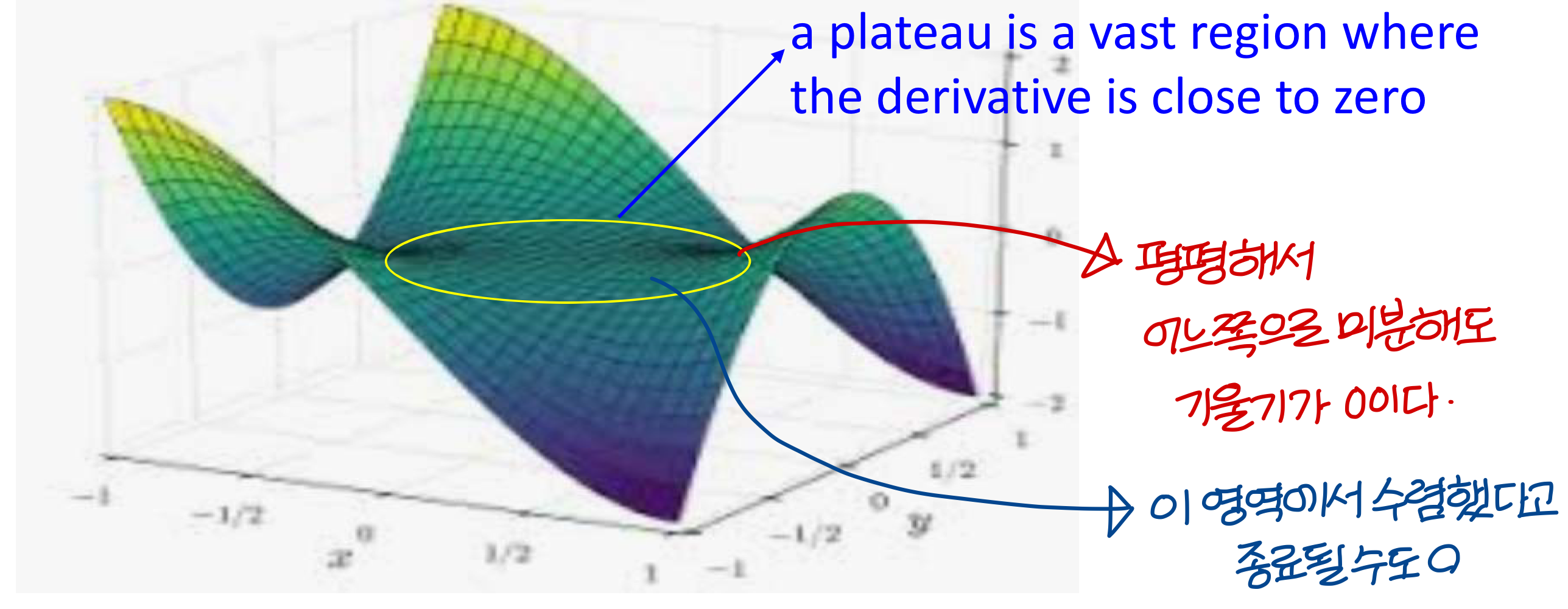
→ 정확히 말하면 0은 아니고 0에 가까운거. 그래서 일어날 가능성이 높음
Uploaded by N2T