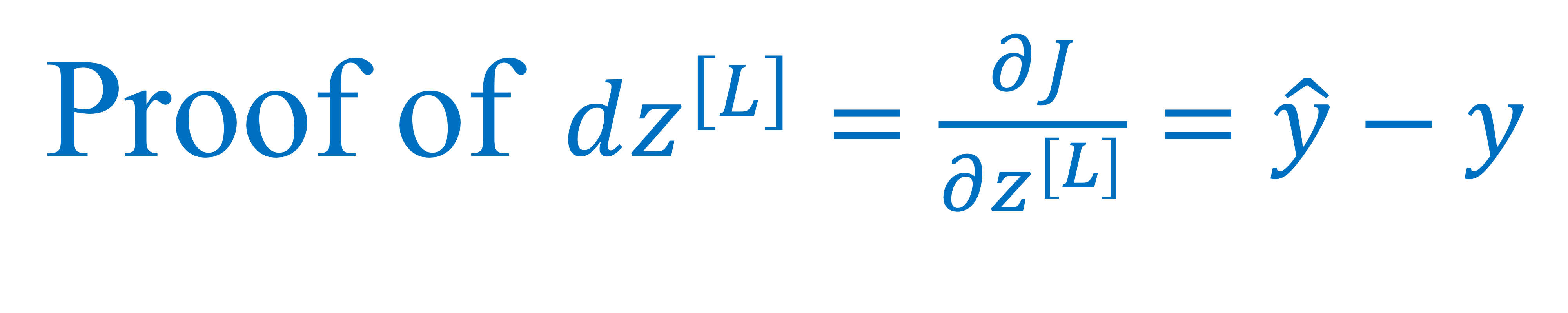- 지금까지 출력은 1개였음
- 근데 출력 여러개일 수 있다. 1개일 때랑 내용이 똑같음
→ softmax function만 이해하면 된다!
→ sigmoid가 softmax의 특이한 케이스임
Recognizing cats, dogs, baby chicks, and others
- 4X1 벡터에서 각 숫자가 의미하는건 이거
첫번째 숫자: 아무데도 포함 안될 확률
두번째 숫자: 고양이일 확률
세번째 숫자: 개일 확률
네번째 숫자: 병아리일 확률
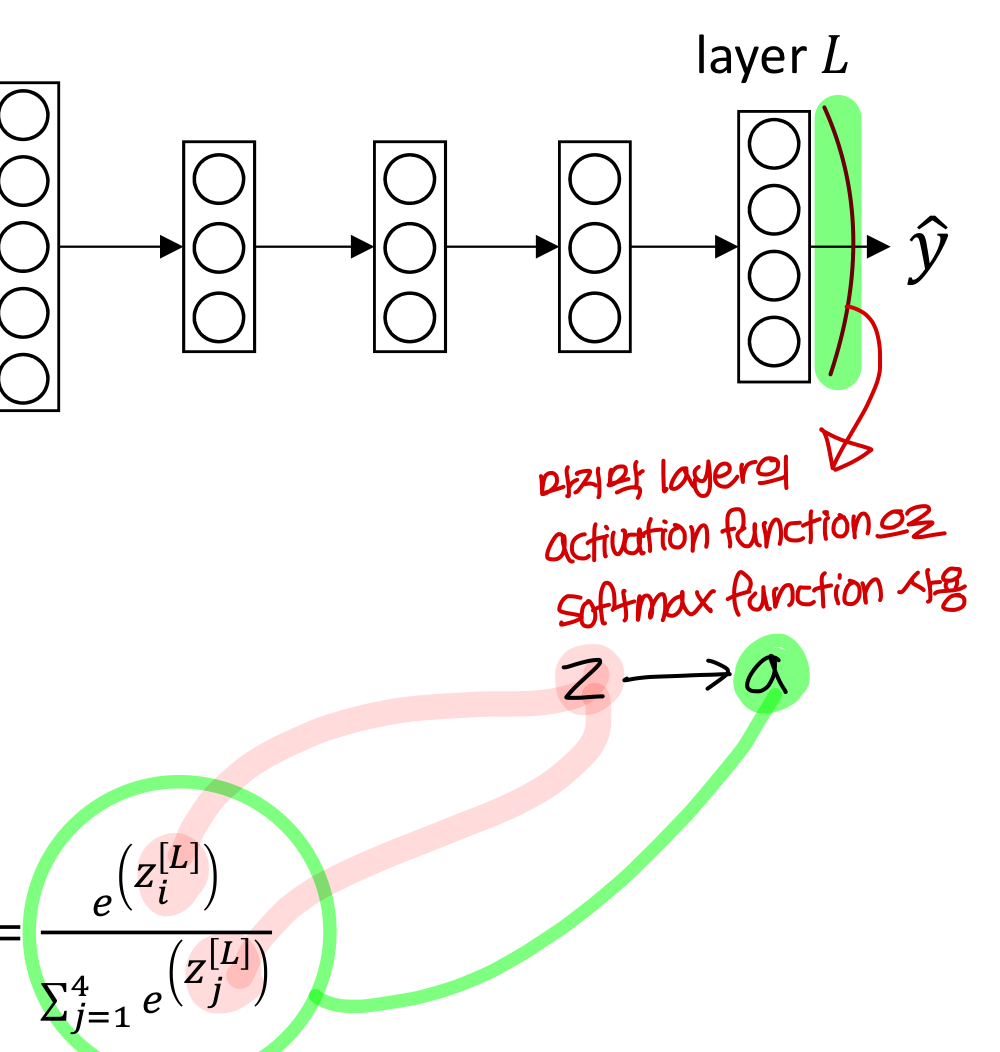
- 마지막 layer의 activation function으로는 softmax function 사용
- softmax 함수를 쓰면 이렇게 다양한 클래스로 나누는게 가능하다!
Understanding softmax
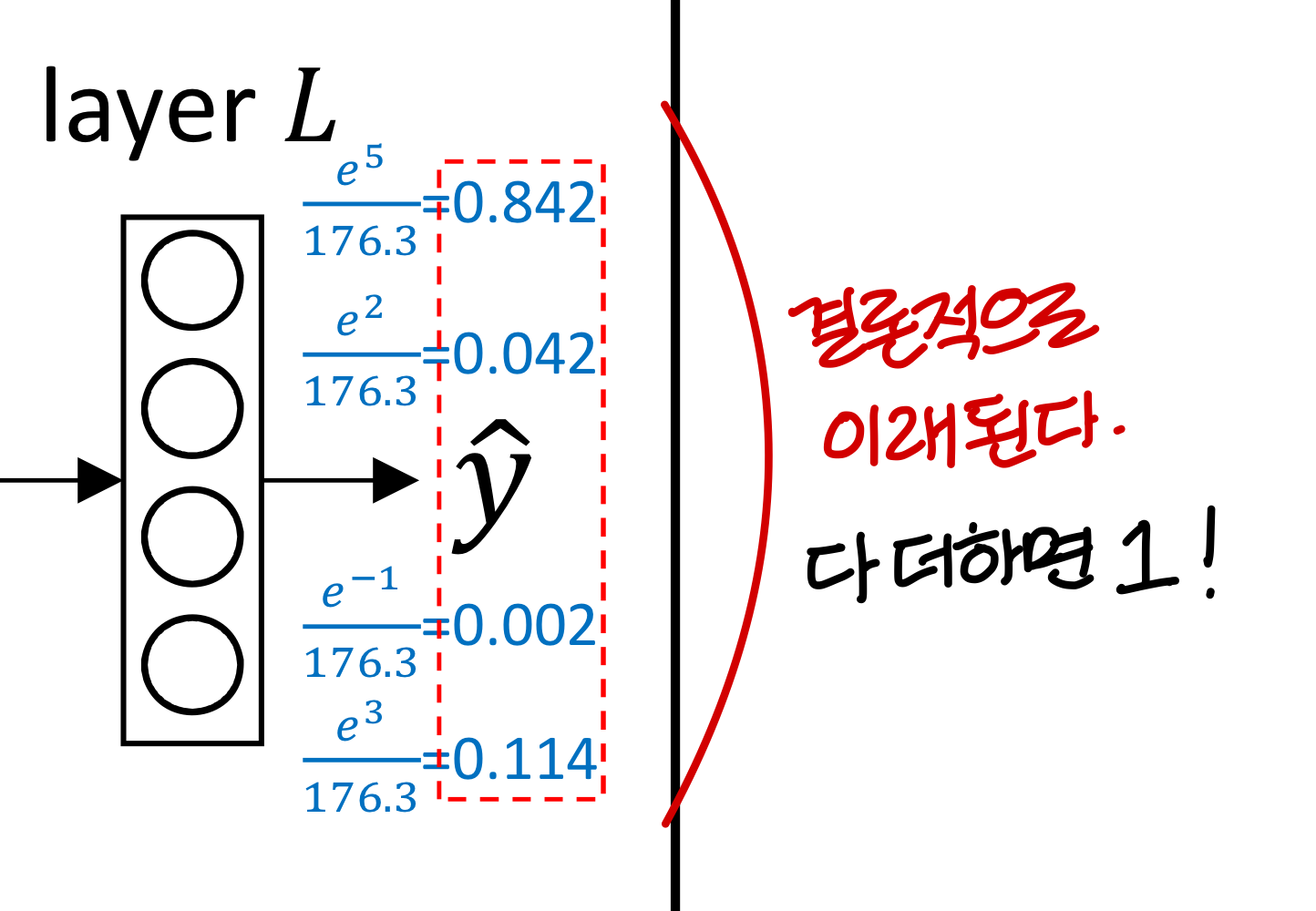
- 왜 결과가 확률이냐고 그러는데
→ 다 합하면 1이고
→ 각 숫자가 0과 1 사이의 값 가지니까
- hardmax랑 비교하기
softmax처럼 하는게 필요할까?무조건 하나가 정답인 문제도 있지만 여러개가 정답인 문제도 있음, 이럴땐 softmax 써야지
이럴 때는 각 출력값마다 threshold를 정해서 판별이 가능함
- C = 2일 때 (class 개수가 2개일 때) softmax는 logistic regression이랑 유사해짐
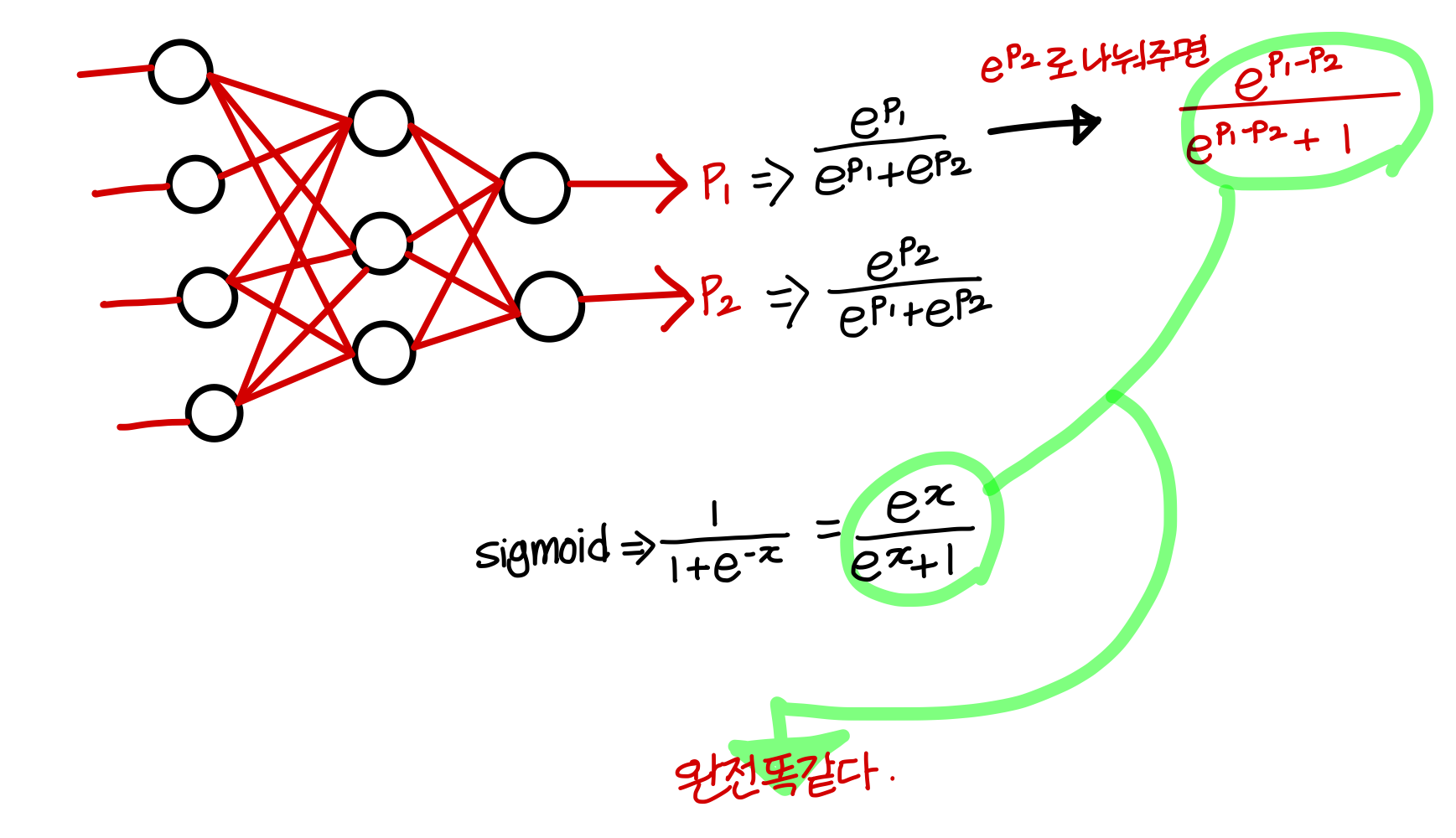💡즉, sigmoid는 softmax의 한 종류일 뿐!💡sigmoid는 C = 2인 softmax에서 인 확률을 학습할 뿐
Loss function
- 이제 결과값이 값 1개가 아니라 벡터임
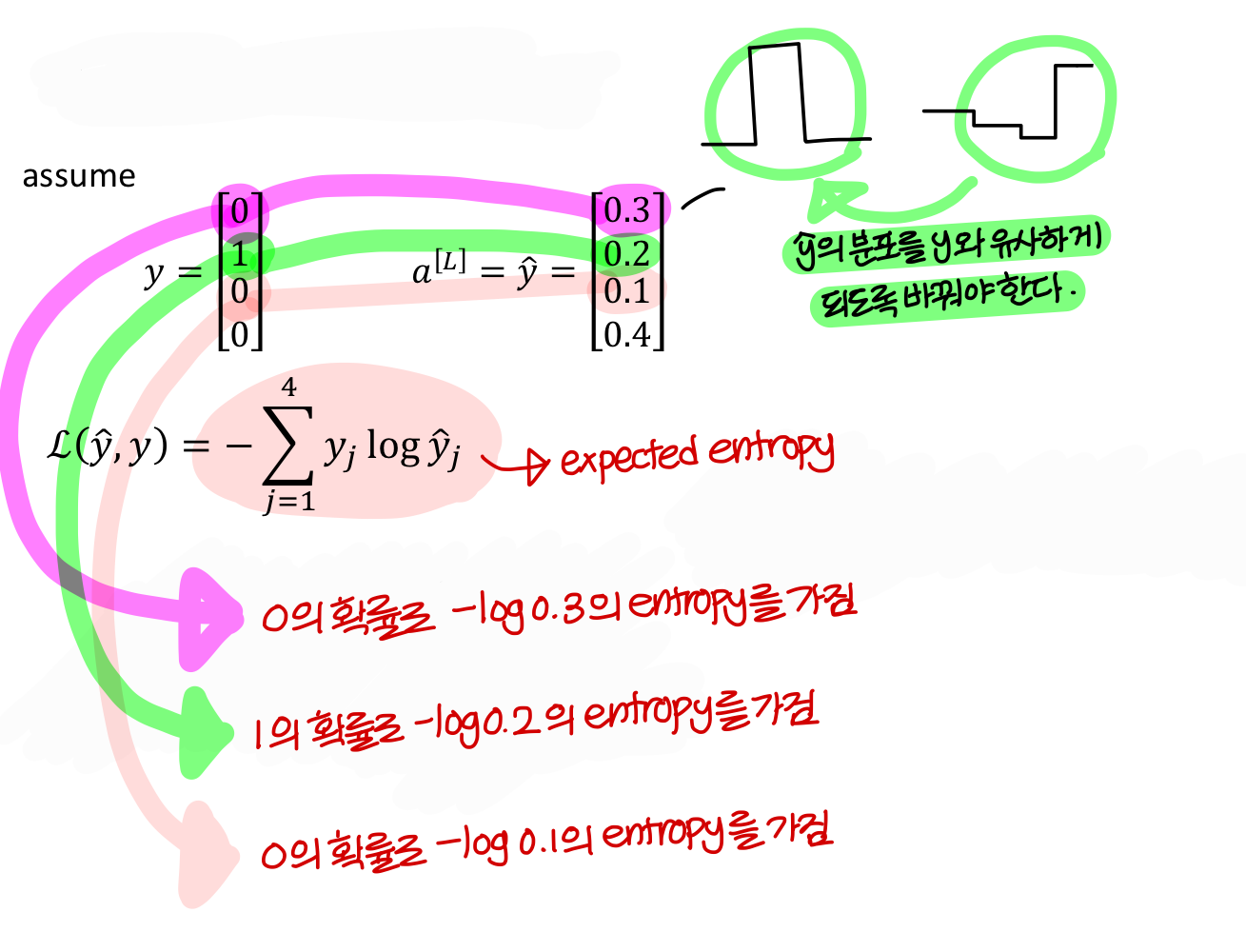
- 이럴땐 loss function 어떻게 쓸까?
→ cross entropy는 y와 y hat의 분포가 완전히 같다고 0이 되는건 아니지만
KL-divergence는 y와 y hat의 분포가 같으면 0이 된다.
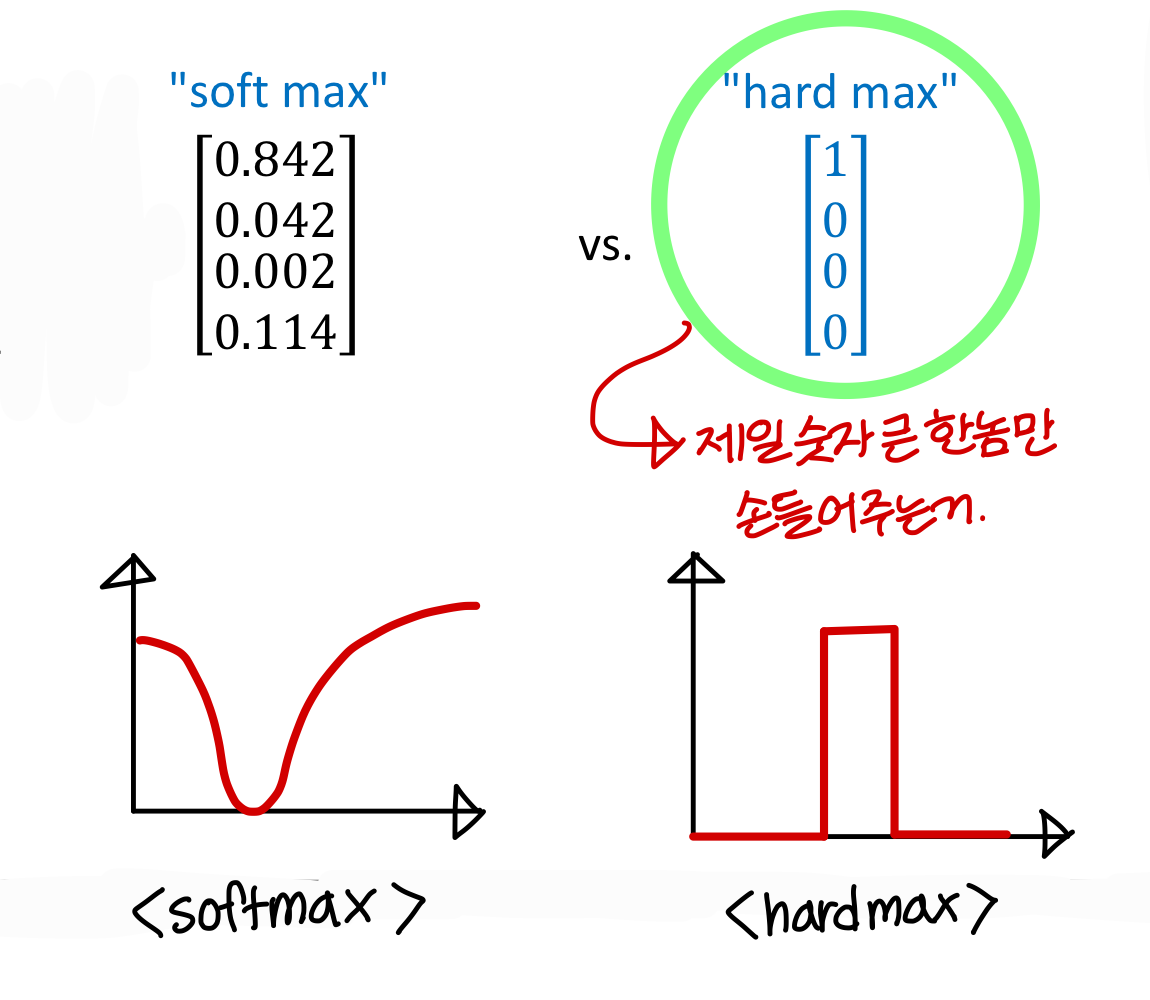
→ cross entropy는 hard max처럼 하나만 1일 필요 없음
합이 1일 때 모두 작동하는 loss function이다!
→ cross entropy 쓸 때 각 숫자의 의미 생각해보면
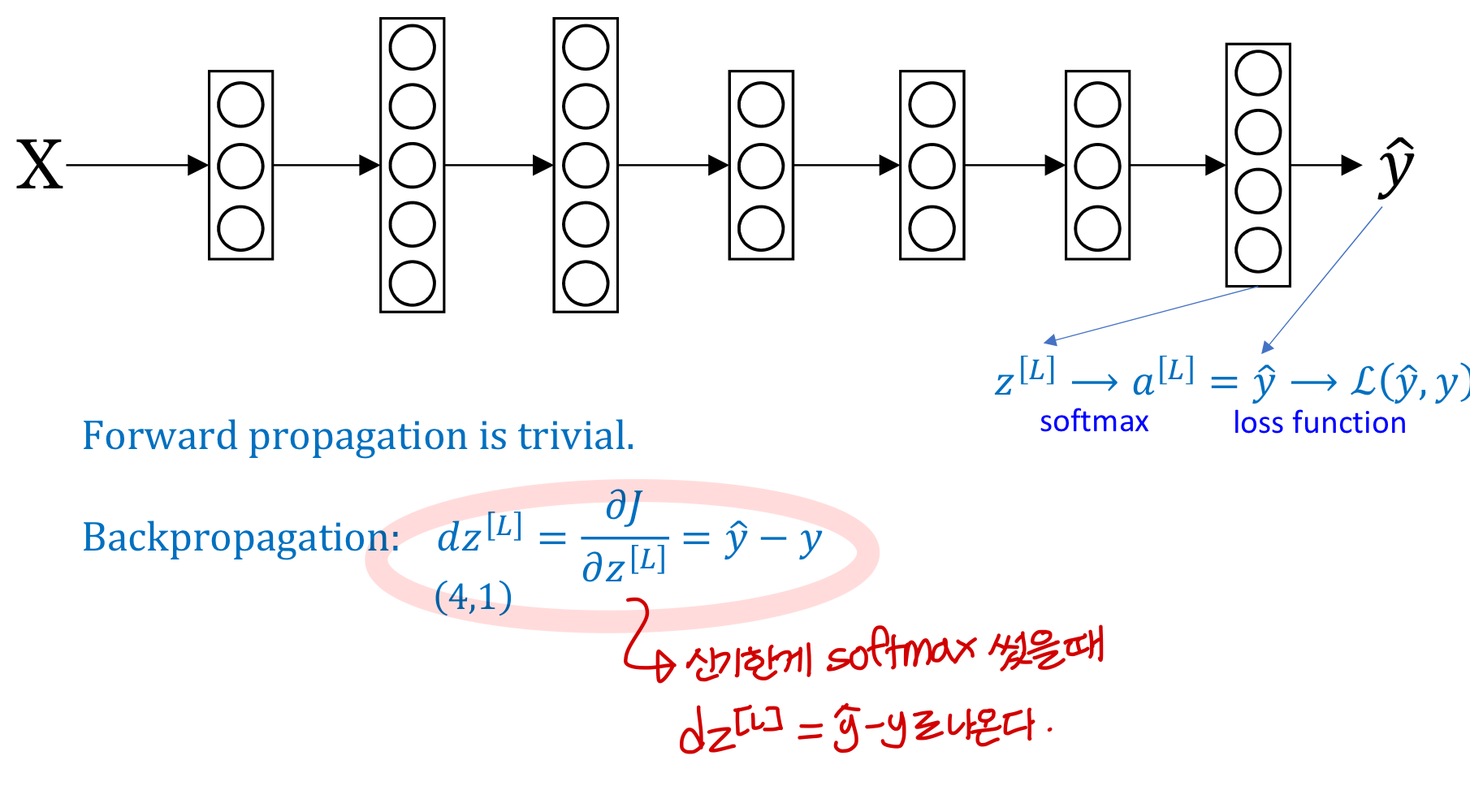
Gradient descent with softmax
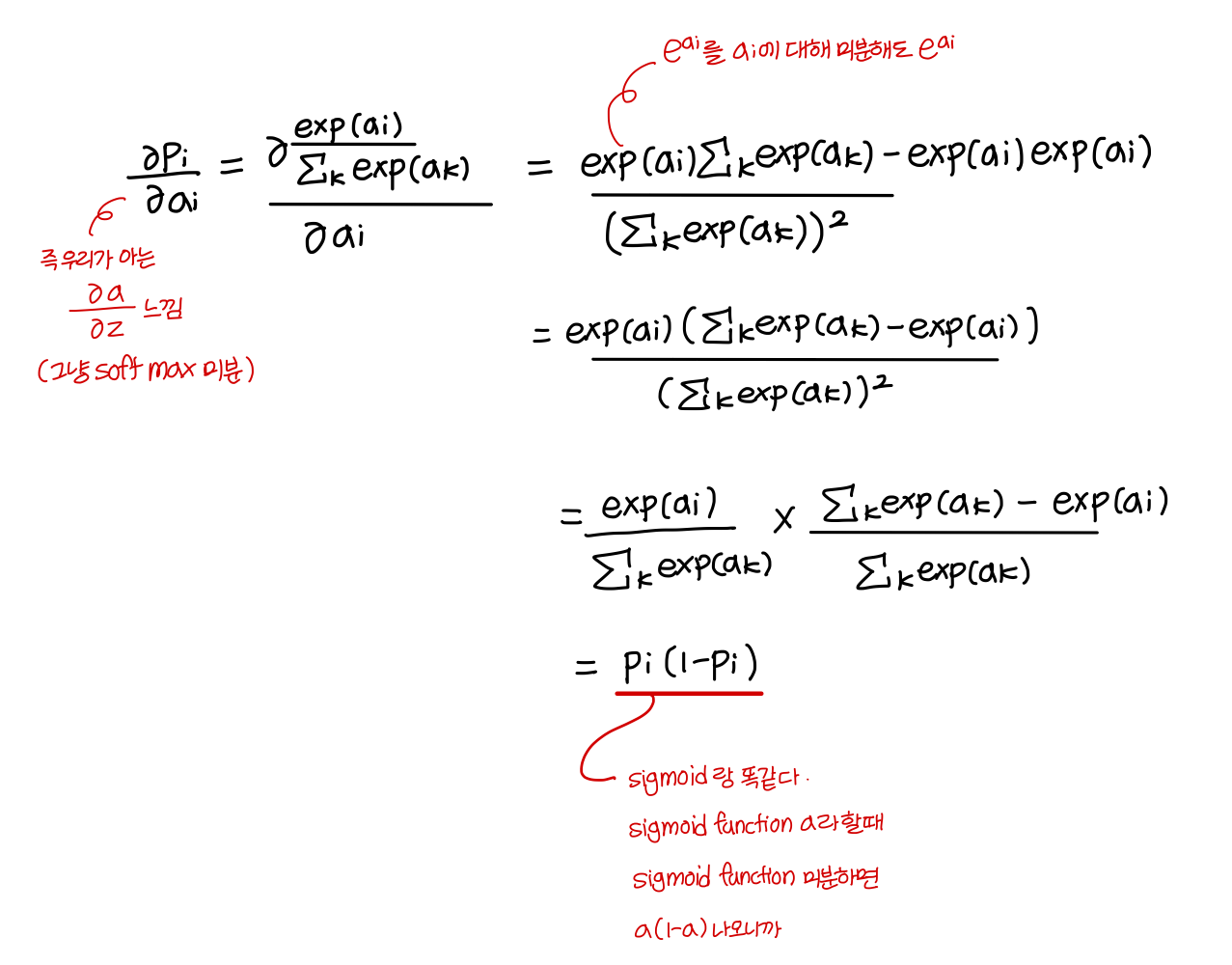
- sigmoid 함수 a라 했을 때
sigmoid 함수 미분하면 a(1-a) 나온다
- softmax 함수 a라 했을 때
softmax 함수 미분하면 a(1-a) 나온다
⇒ 이 사실 사용해서 dz 구하면 (y hat - y) 나옴
<증명>
→ 이 사실을 증명할거임!
- 표기는 이렇게
- step 1
- step 1 → 다른 케이스
- step 2
Uploaded by N2T