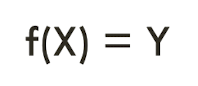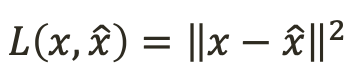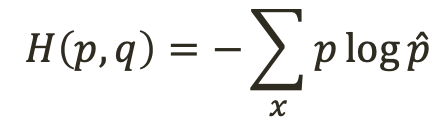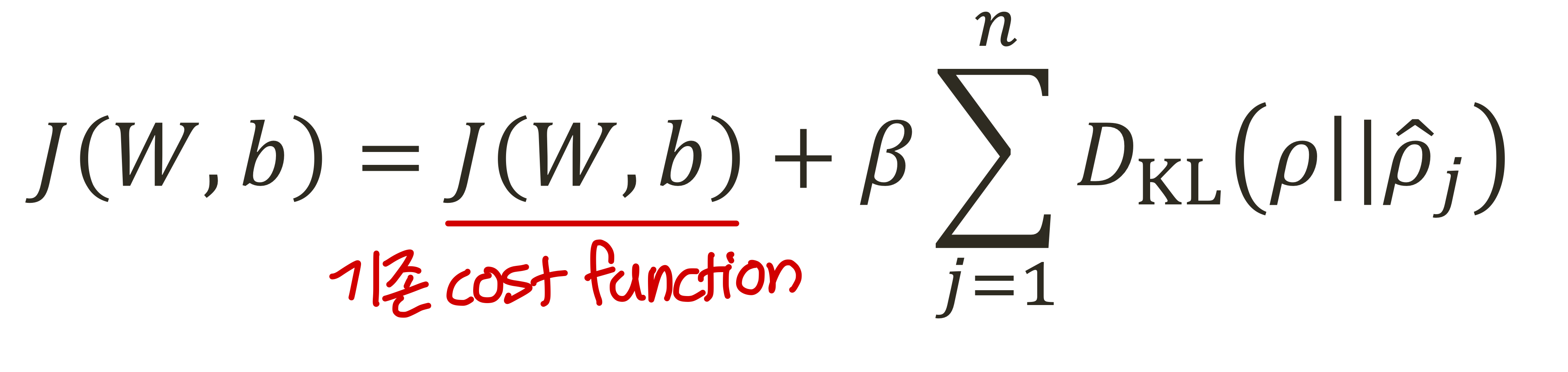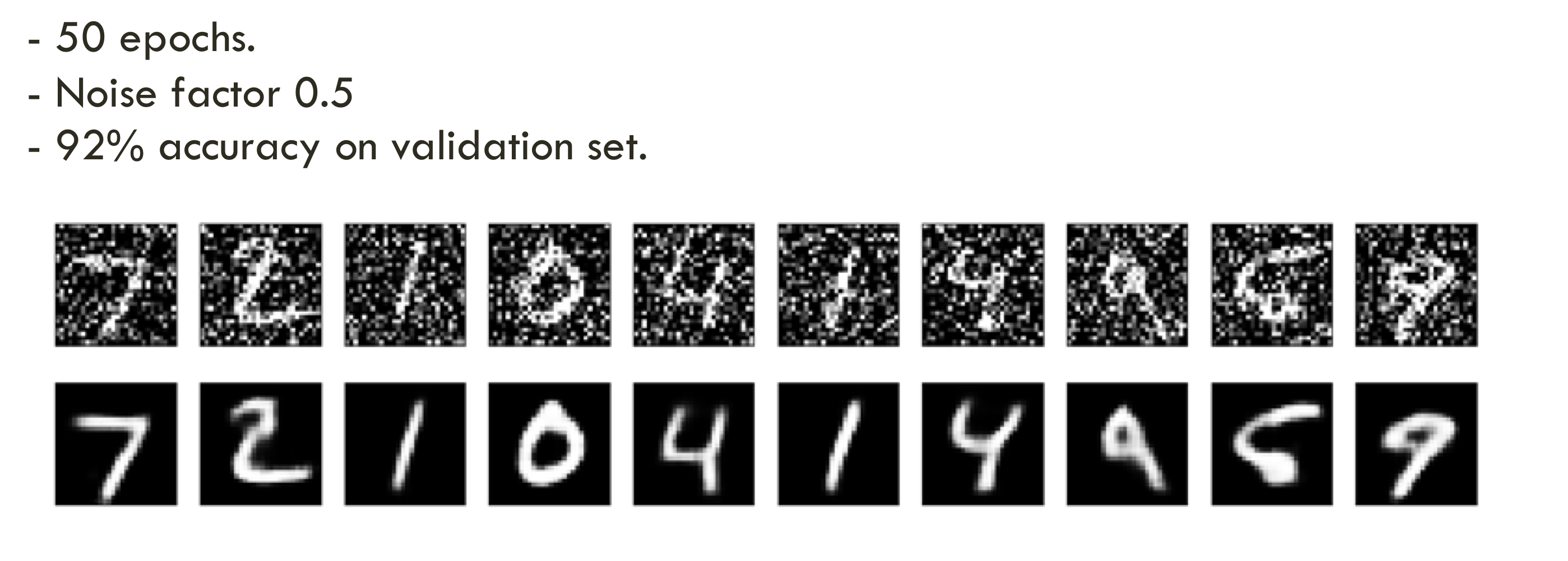- 이때까지 한건 Supervised learning
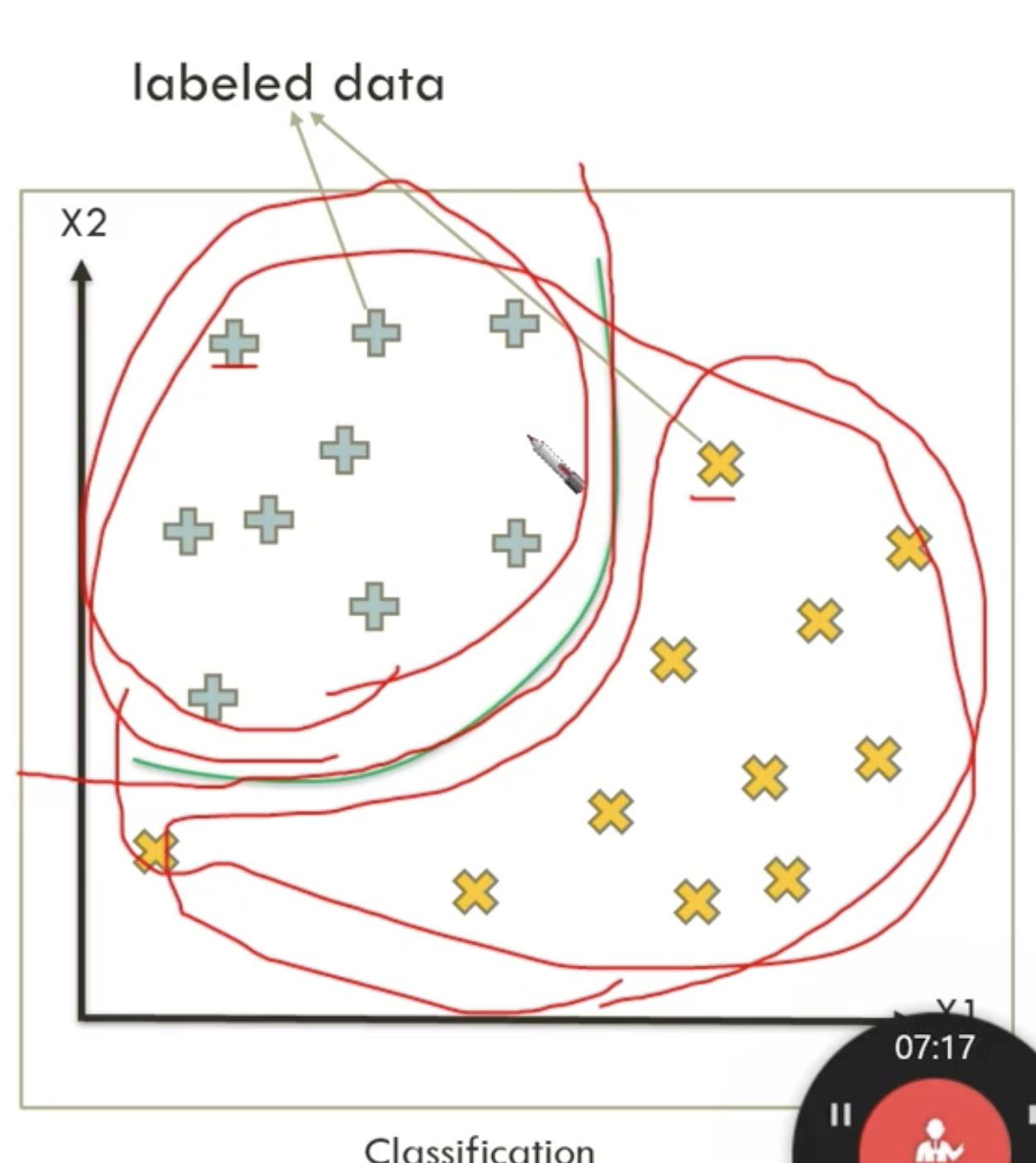
→ labeling한 데이터를 주는거
- 지금부터 살펴볼건 Unsupervised learning
→ labeling 안해주고 알아서 분류해라 하는거 ground truth를 안준다.
→ 대신 입력값이 생성되는 원리를 학습하거나 입력값을 알아서 clustering 해라!
Supervised learning
- ex)
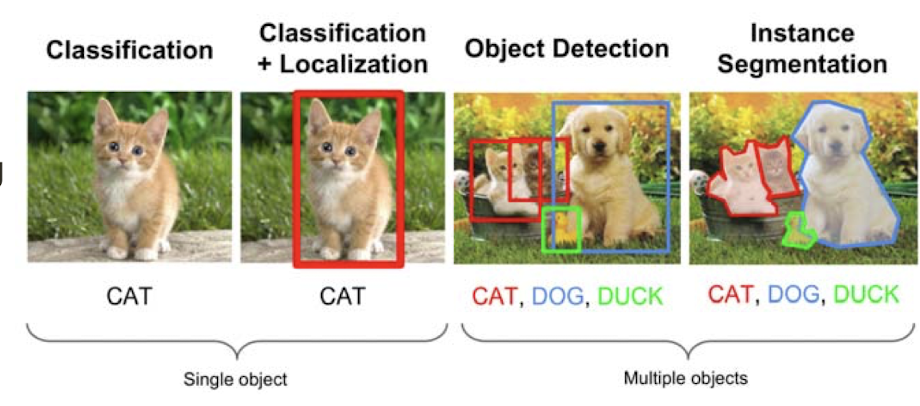
→ Single object가 있을 때 뭔지 판별만 하는거: Classification model
→ Single object가 있을 때 뭔지 판별하고 어디있는지 박스 만들어주는거: Classification+Localization model
→ Multiple objects가 있을 때 어디에 뭐가 있는지 박스 만들어서 판별해주는거: Object Detection model
→ Multiple objects가 있을 때 어디에 뭐가 있는게 경계를 만들어서 판단해주는거: Instance Segmentation model
- ex:
regressionlabeled data가 이렇게 있으면
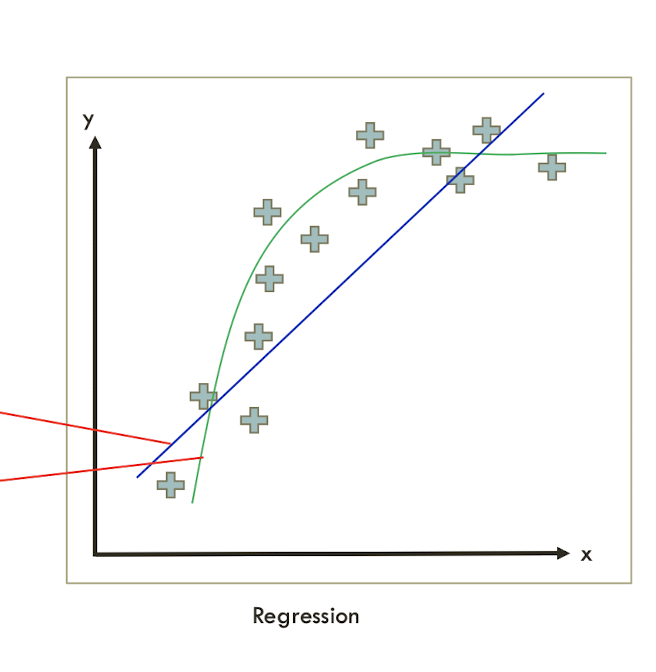
→ linear regression을 쓰면 직선으로 표현을 하는거고
→ logistic regression(linear + sigmoid)을 쓰면 곡선으로 표현을 하는거고
Supervised learning vs Unsupervised learning
- label이 틀리거나 (x_1, y_1) 이렇게 주어졌는데 y_1가 틀렸거나
- training data 군데군데 label이 비어있거나
- 아니면 label이 아예 안되어 있거나
⇒ 이런 상황에서는 Unsupervised learning이 필요!
Unsupervised learning
- Unsupervised learning의 목표는
data의 structure를 파악하는거(또는 data feature들 간의 관계성을 학습)
- 언제쓰나?
: Clustering, Compression(압축), Feature & Representation learning,
Dimensionality reduction(차원 줄이기) 등...
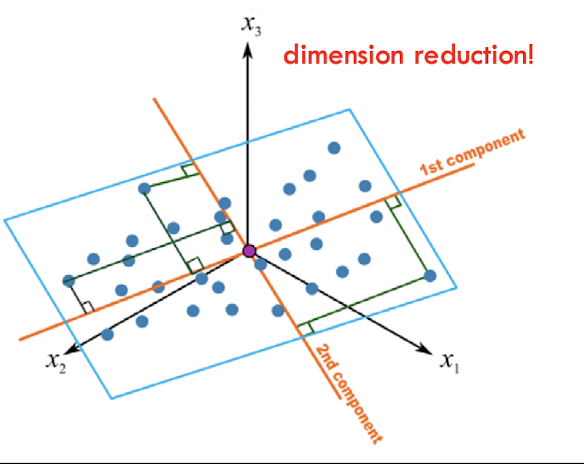
PCA- Principle component analysis
- data compression이랑 visualization 하는데 사용되는 통계적 approach
- 일종의 regression 문제로 볼 수 있음) 점과의 차이가 제일 작은 평면을 찾는거!
- 문제점: 모든 계산을 linear combination으로만 한다
hyperplan을 곡선으로는 못만든다.
Traditional autoencoder
neural net의 unsupervised leraning
- traditional autoencoder는 neural net으로 되어 있기 때문에 곡면을 만들 수 있음
PCA는 평면의 형태로만 차원 축소가 가능한데 이건 곡면의 형태로 차원 축소가 가능하다
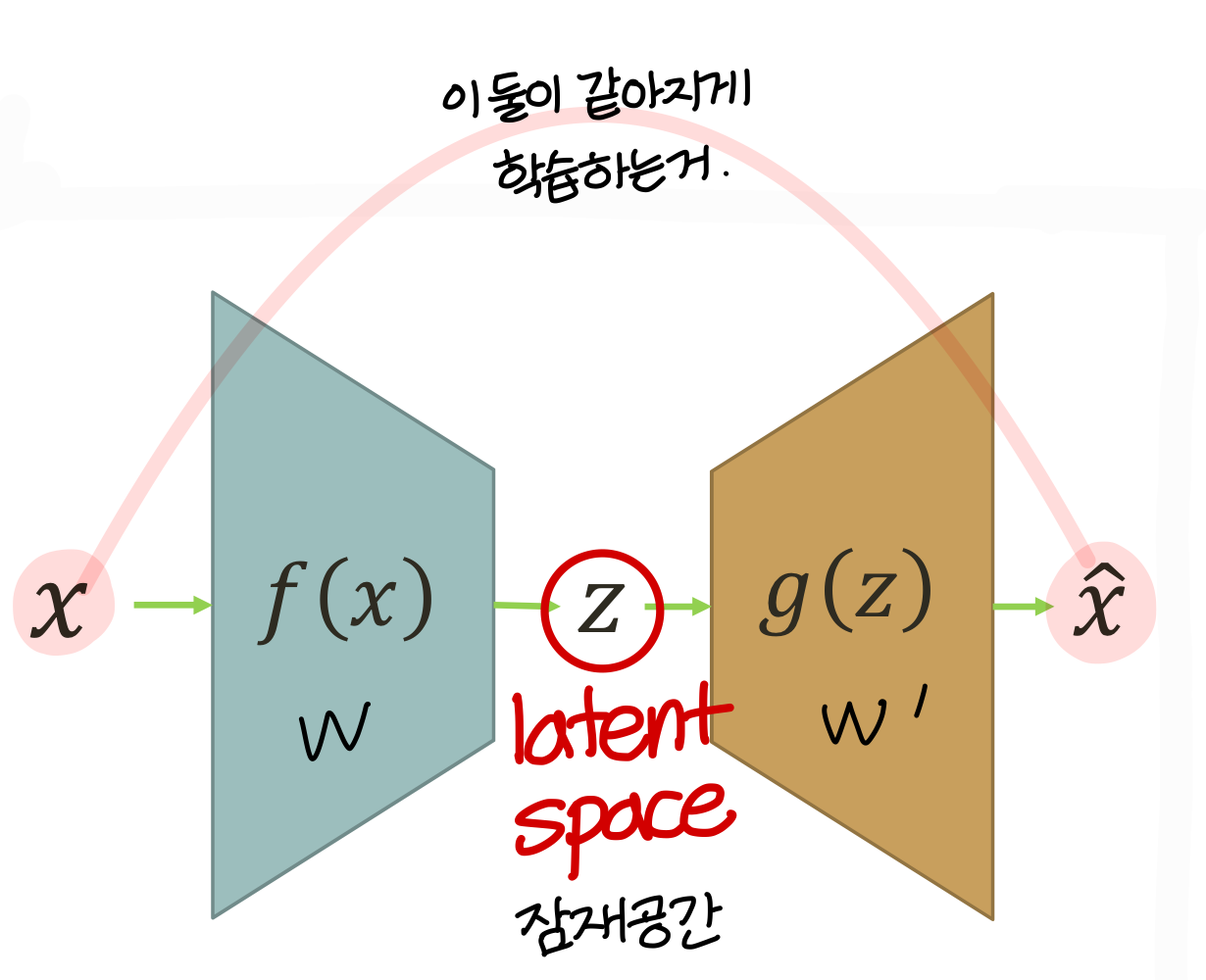
- supervised learning에서 학습시키는게 (X, Y)라면
여기서 학습하는건 (X, X’)
- 차원 redution을 하면 정보 소실 거의 없이 뉴런 수를 줄일 수 있다
- 따라서 복원했을 때 살짝 틀려도 상관없는 경우(ex: 사진, 비디오)
→ neural net을 사용해 compression을 하면된다.
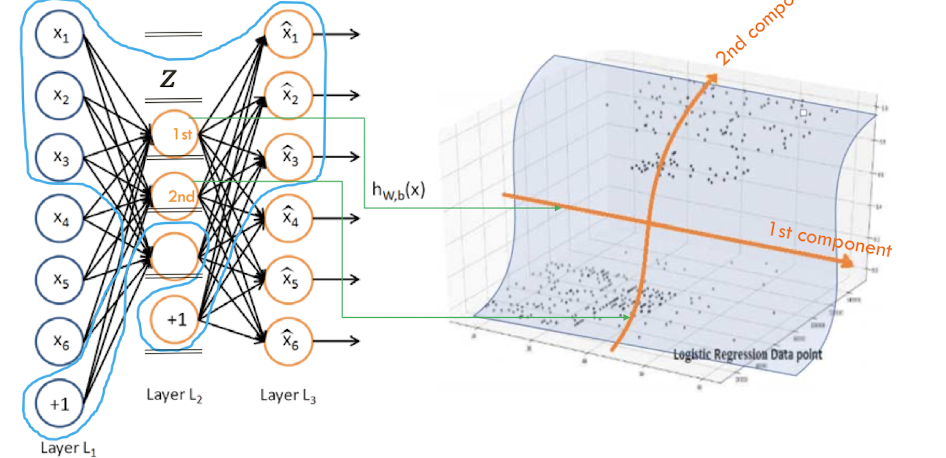
→ 학습이 잘되면 결과적으로 파란 곡선처럼 된다.
- 3차원 점이 x_1, x_2, x_3로 들어가고 +1은 bias 값이라고 보면 됨
- 중간에 보이는 1st, 2nd가 2차원으로 표현된 좌표
→ 이런식으로 3차원을 2차원으로 표현할 수 있음
Uses
- 차원을 줄이고 feature를 학습하는데 도움이 된다
- 근데 이거 막 쓰면 안됨. 이미지처럼 픽셀 몇 개 망가져도 되는 그런 곳에 써야지
C 코드나 자연어 같은거 하면 안됨. 하나만 망가져도 큰일나니까
Simple Idea
- 이때 hidden layer에 regularization 같은 기법을 써서 좀 더 완고하게 학습되게 함
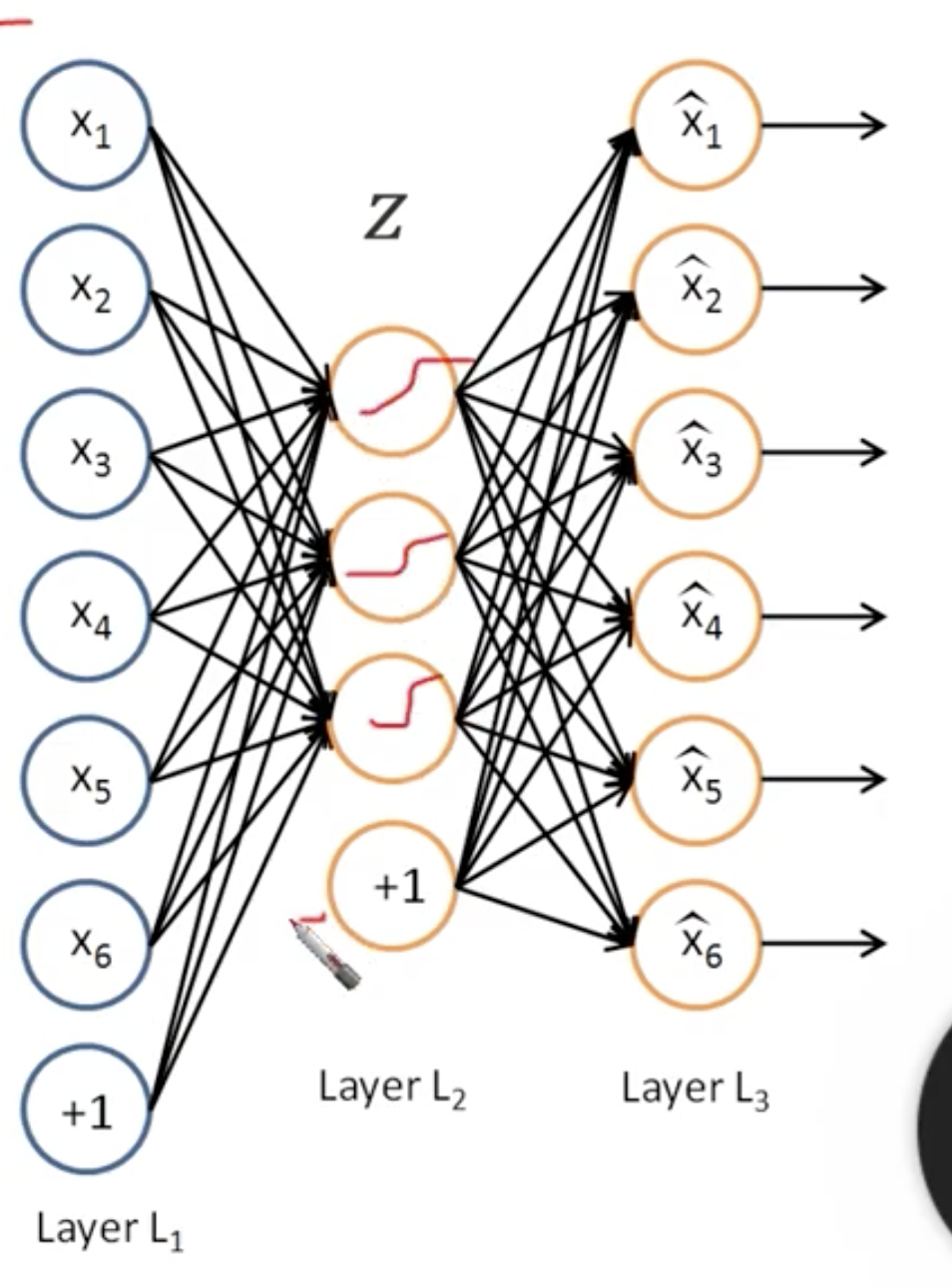
구조 뜯어보자!
- 전체 아키텍쳐를 auto encoder라고 하고
→ 이건 encoder랑 decoder로 구성된다
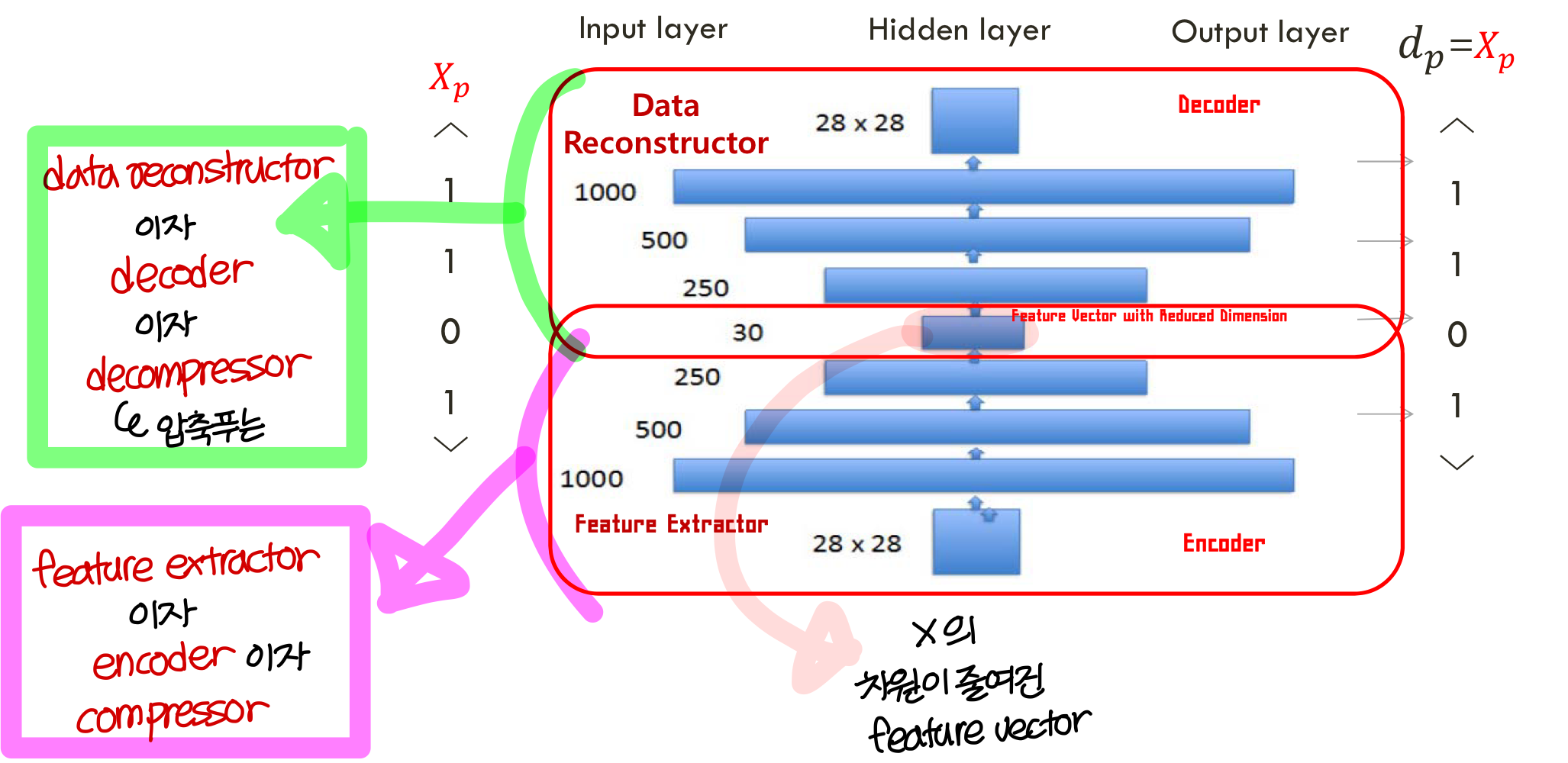
Training the AE
- Auto encoder training 하는 방법: 일반적인 deep neural network랑 동일하다
- 입력만으로 학습을 한다! (X, Y)가 아니라 (X, X)를 넣어서 loss function 쓰면 된다
<loss function>
Undercomplete AE vs Overcomplete AE
AE structure에 2가지 타입이 있음 - under complete AE, over complete AE
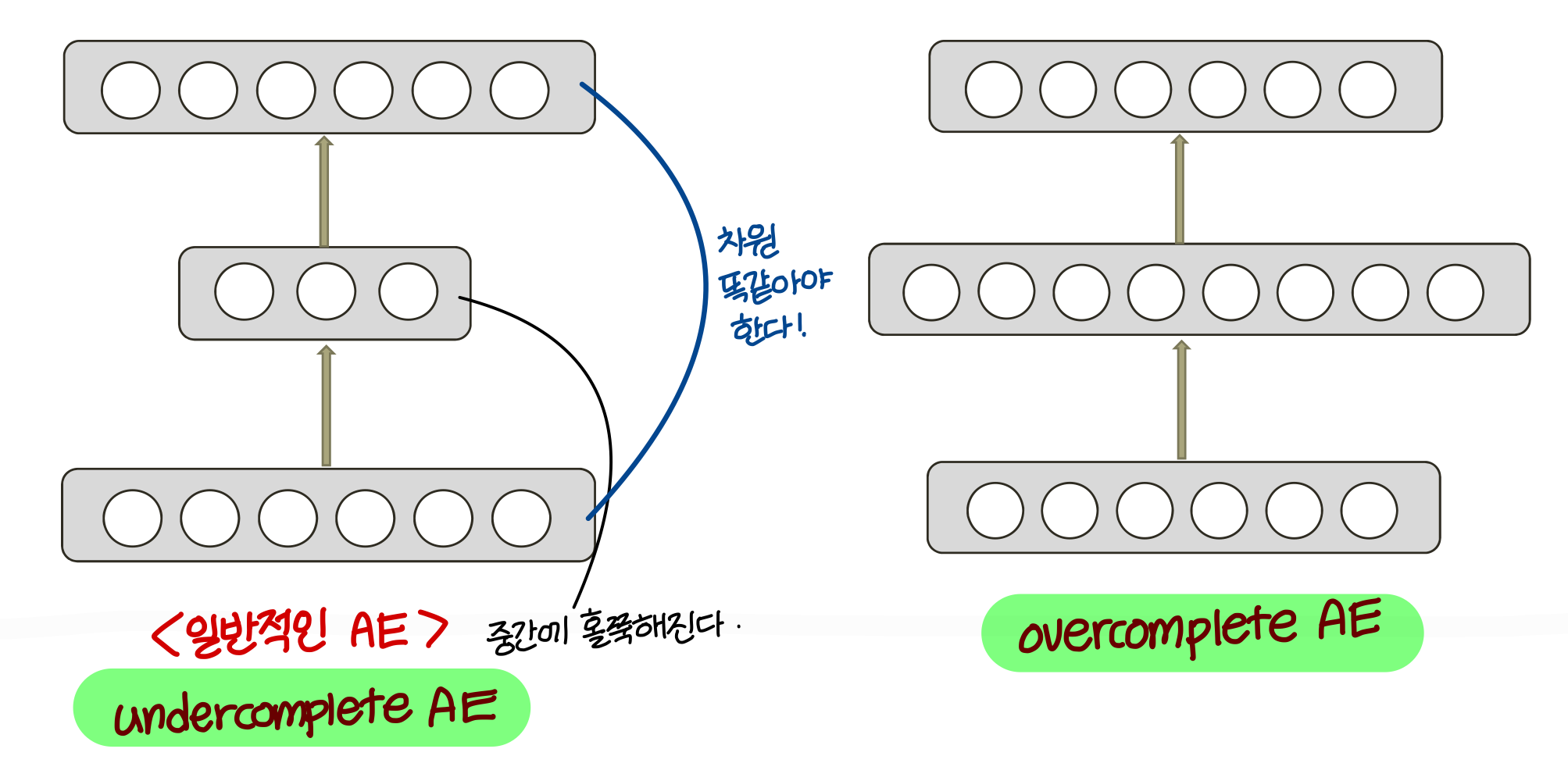
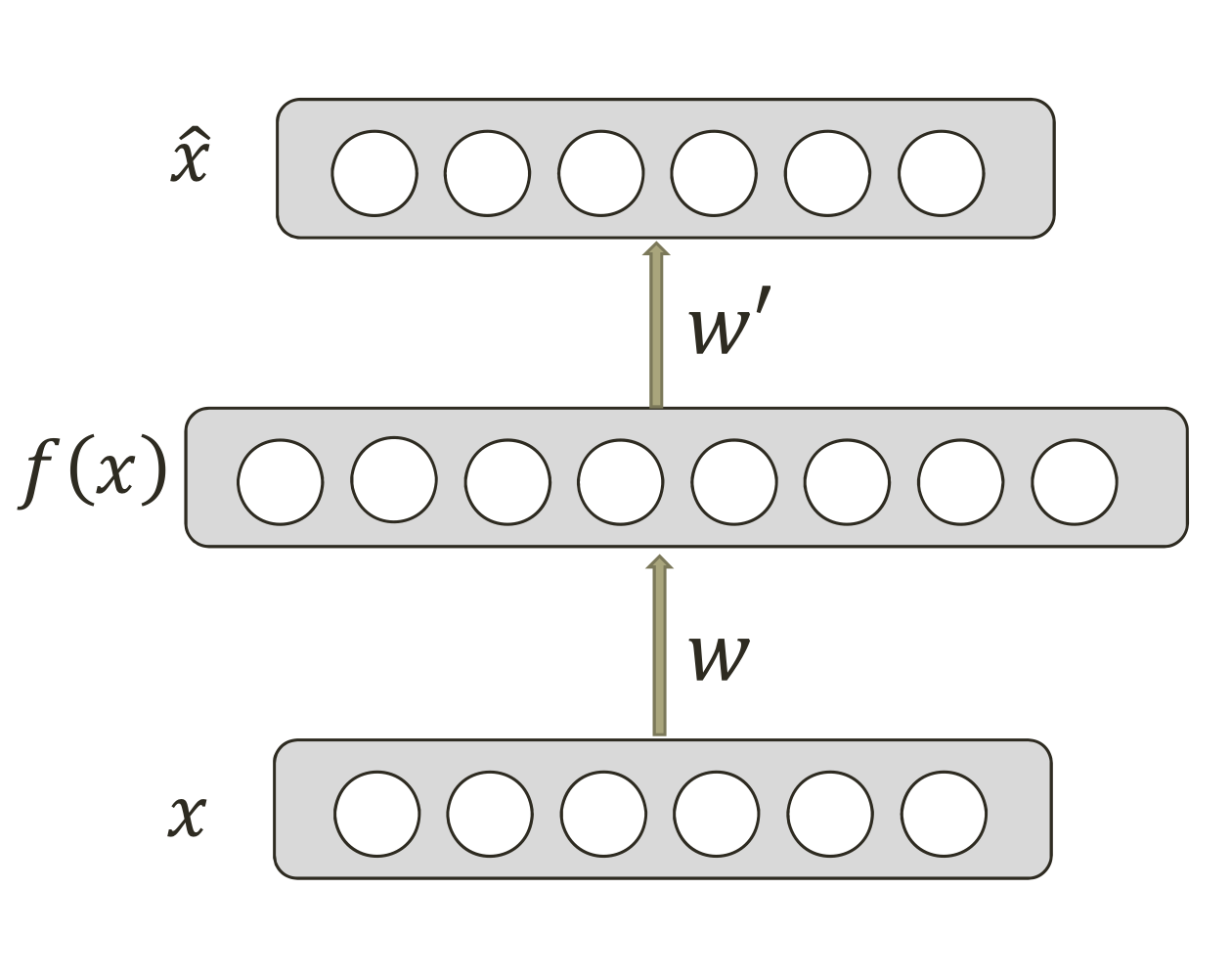
Undercomplete AE
- input data의 차원을 줄임
- 너무 복잡한 training data의 distribution을 잘 정리해줌
- 근데 under complete AE가 적합하지 않은 AE가 있을 수 있음
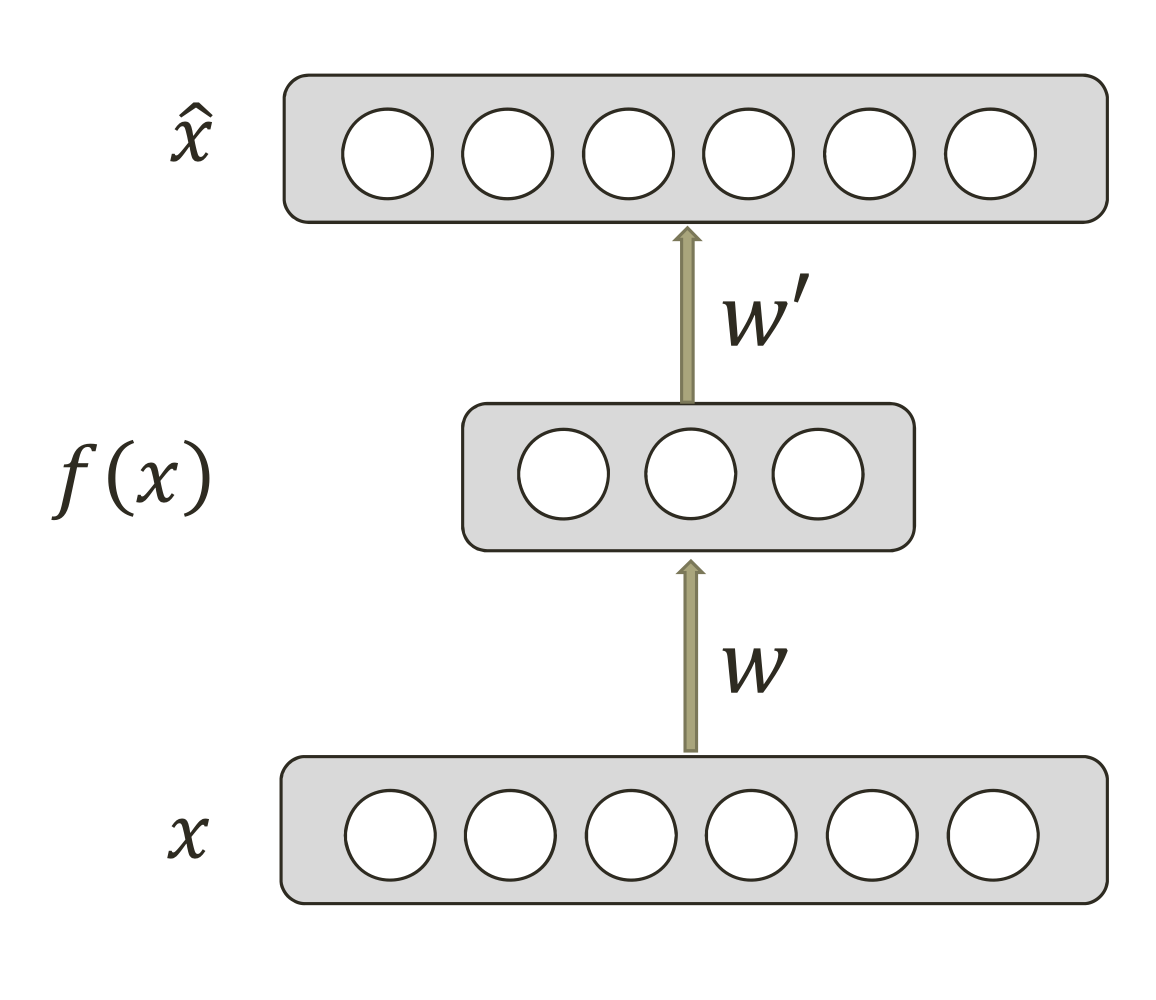
Overcomplete AE
- 매우 복잡하고 nosiy해서 규칙 찾아내기 어려운
그런 data에 적합한 경우가 있음
ex) 동영상, 이미지)
- 일반 함수를 modeling 할 때 쓰기도 함
- 각 input data component 간의 경우의 수 너무 많으면
hidden layer의 dimension이
input, output dimension보다 크도록 만드는게 도움됨
- overcomplete AE는 overfitting이 일어날 가능성이 있음
- undercomplete AE와는 다르게 hidden units이
meaningful structure를 extract할거라는 보장이 없음
<극단적인 경우>
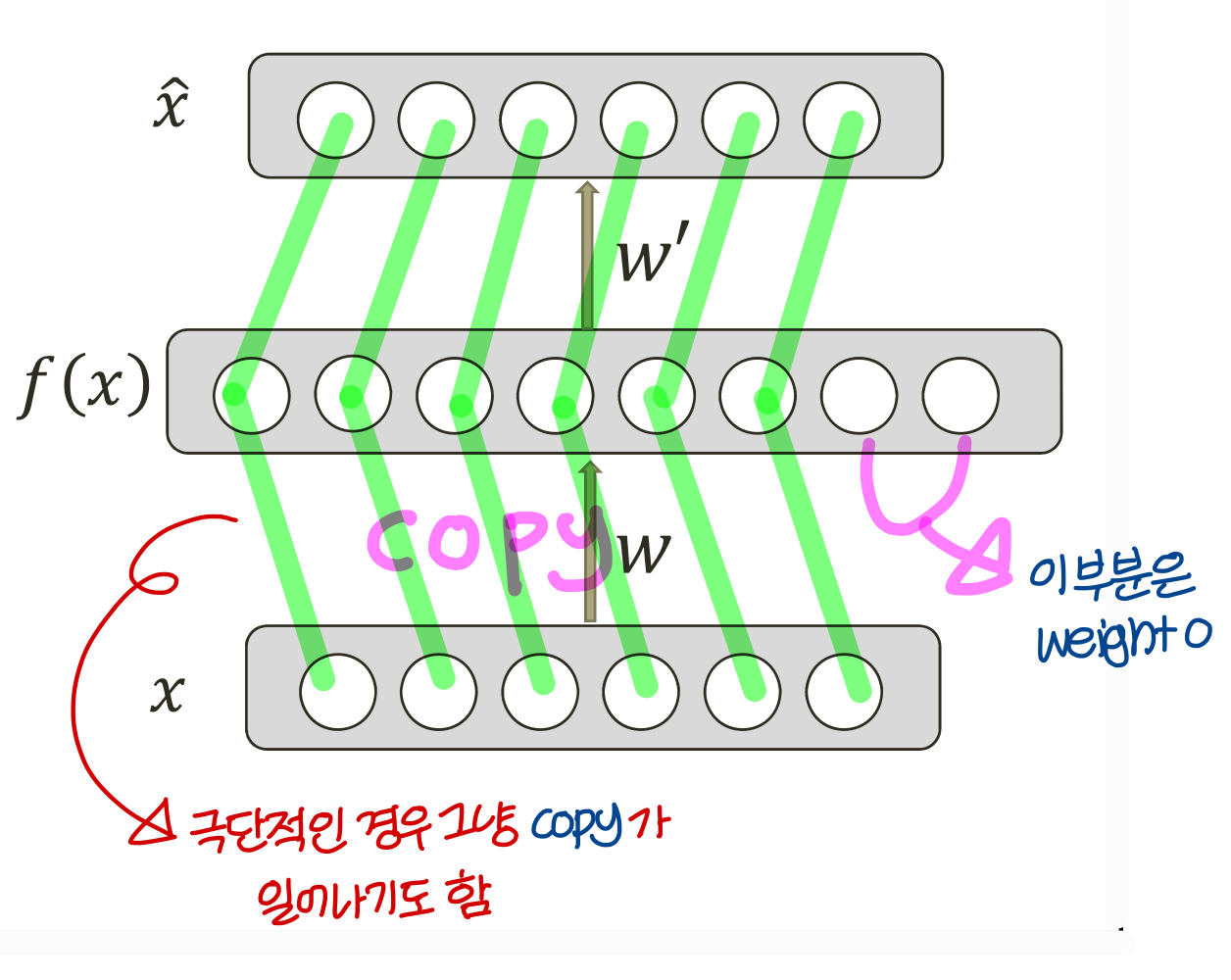
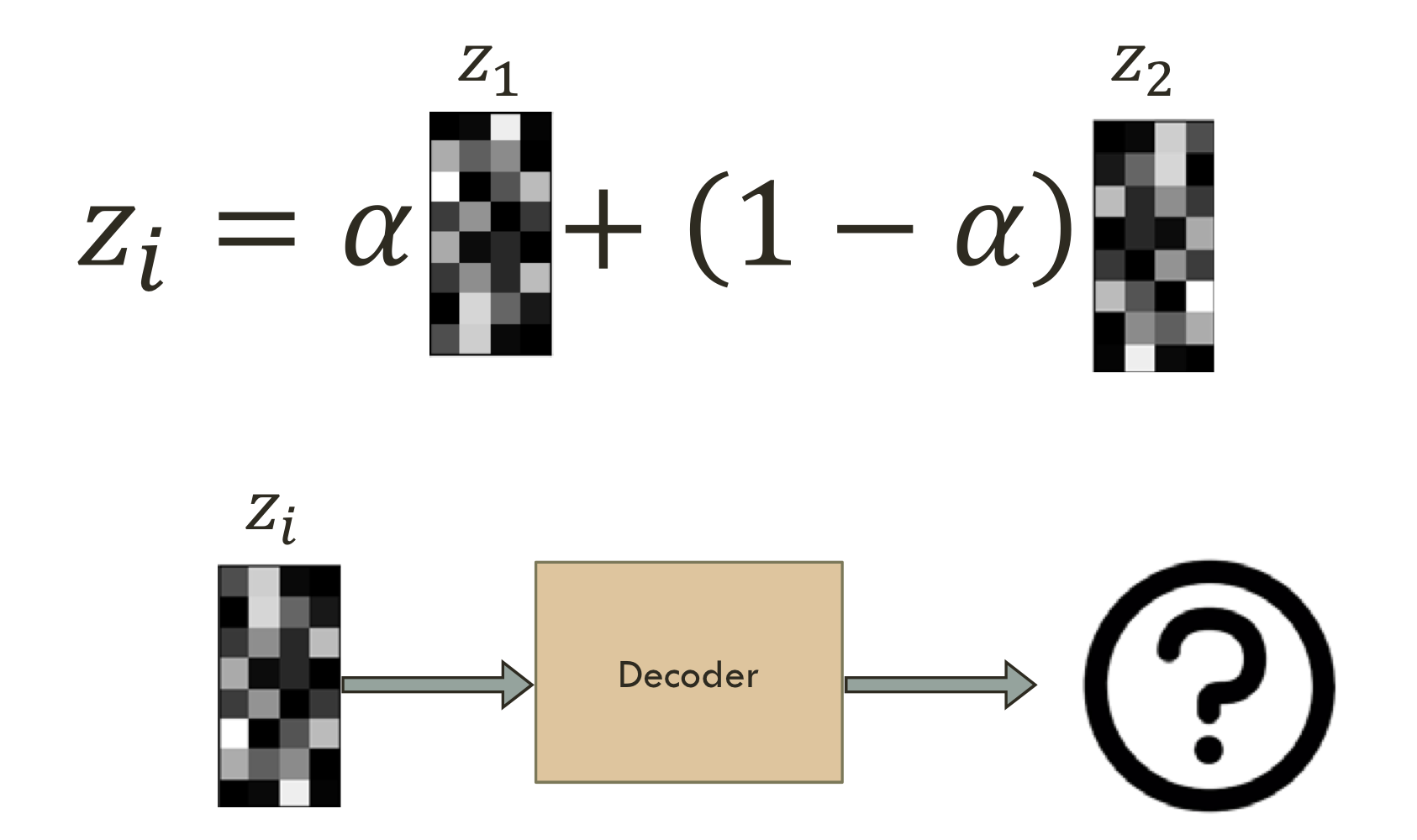
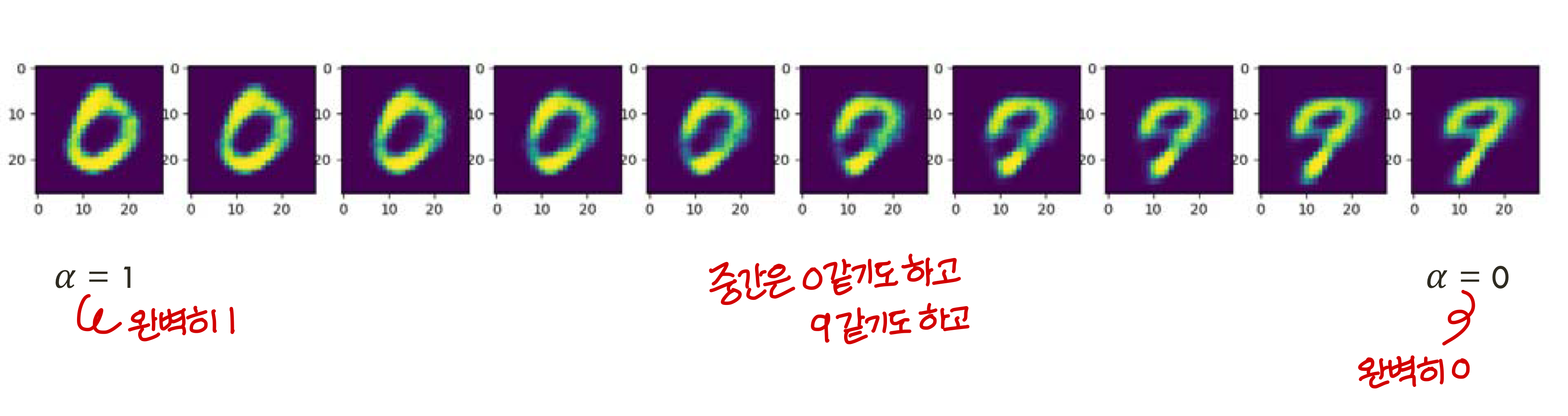
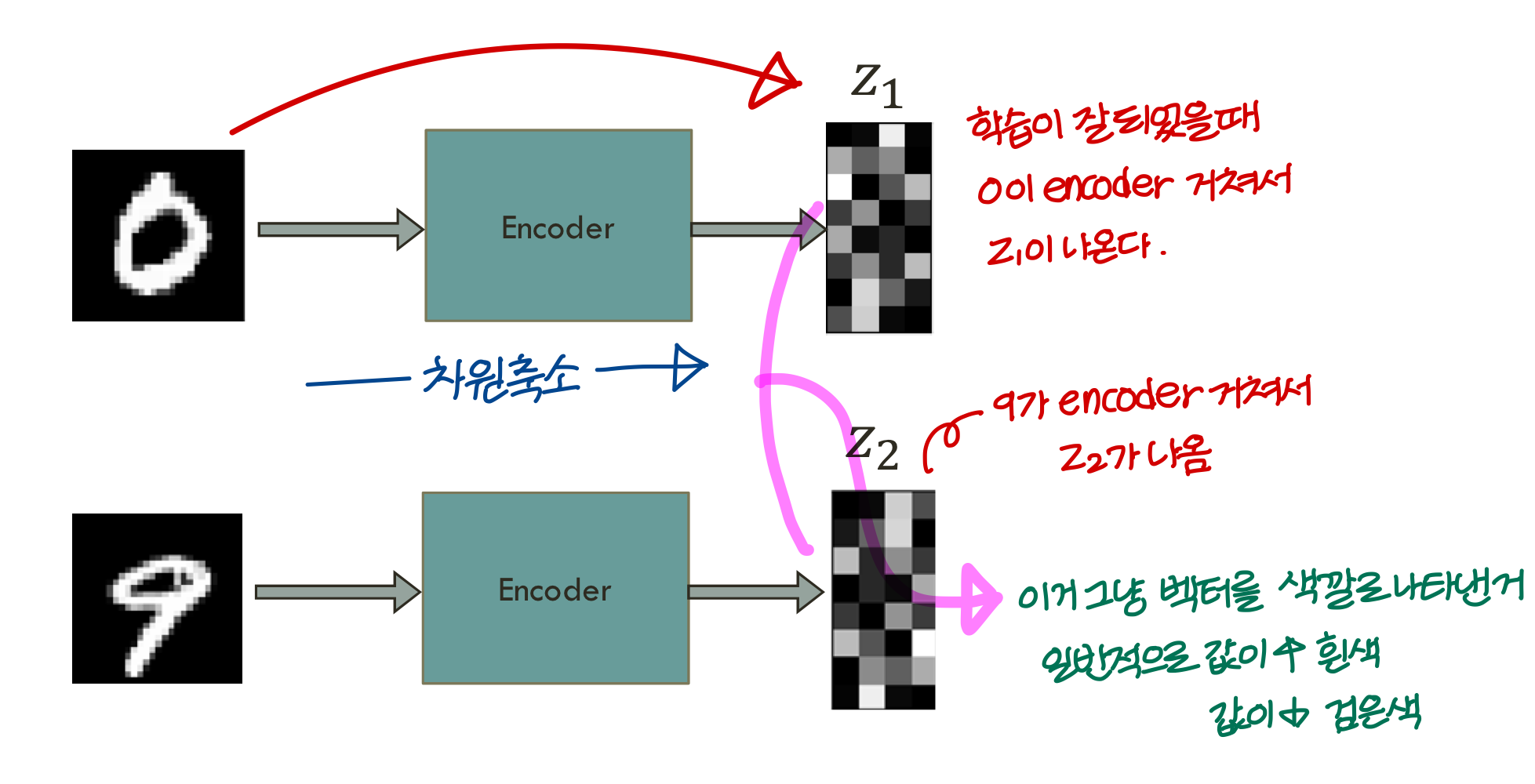
Simple latent space interpolation
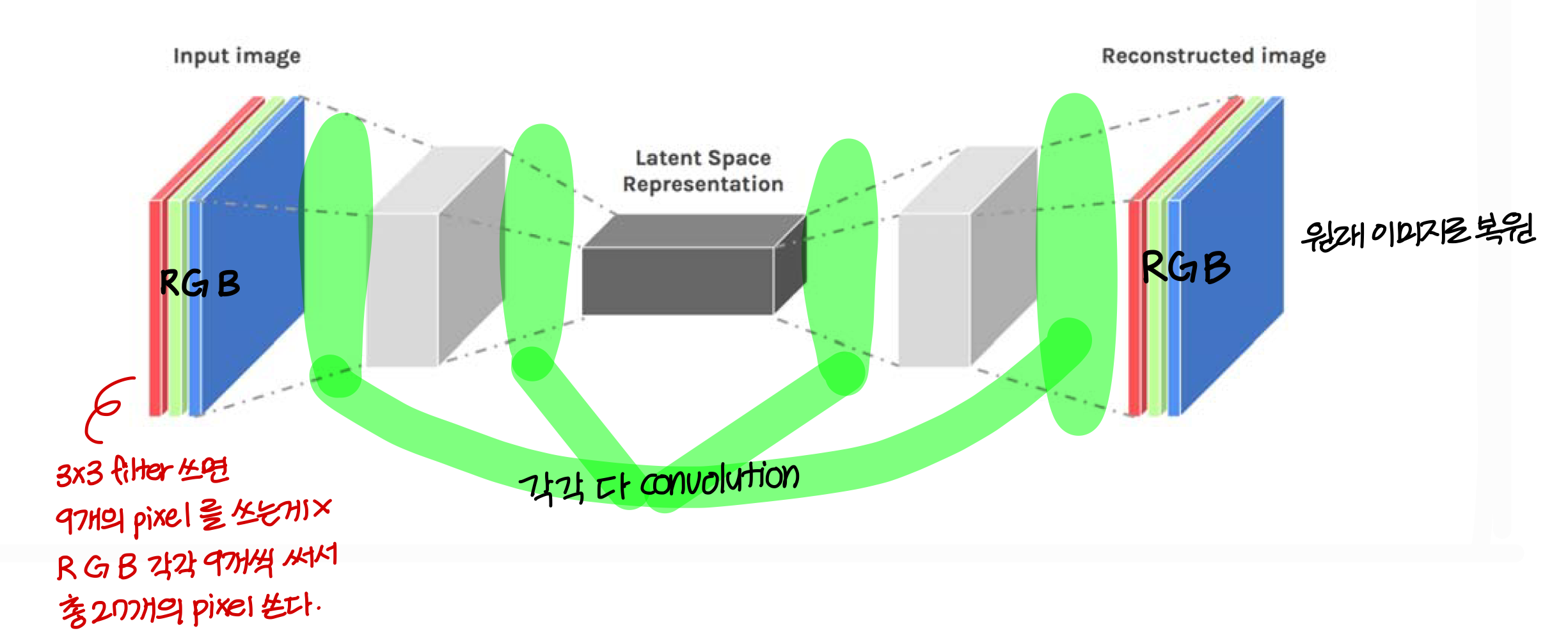
Convolutional AE
→ 실제 이미지에 대해서 auto encoder를 만들 때는 그냥 fully connected AE를 쓰는게 아니라 convolutional AE를 쓴다!
- fully connected layer에서는 image 일렬의 벡터로 변형해서서 사용함
- convolutional layer에서는 image 원형 그대로 둠. 일렬의 벡터로 변형 X
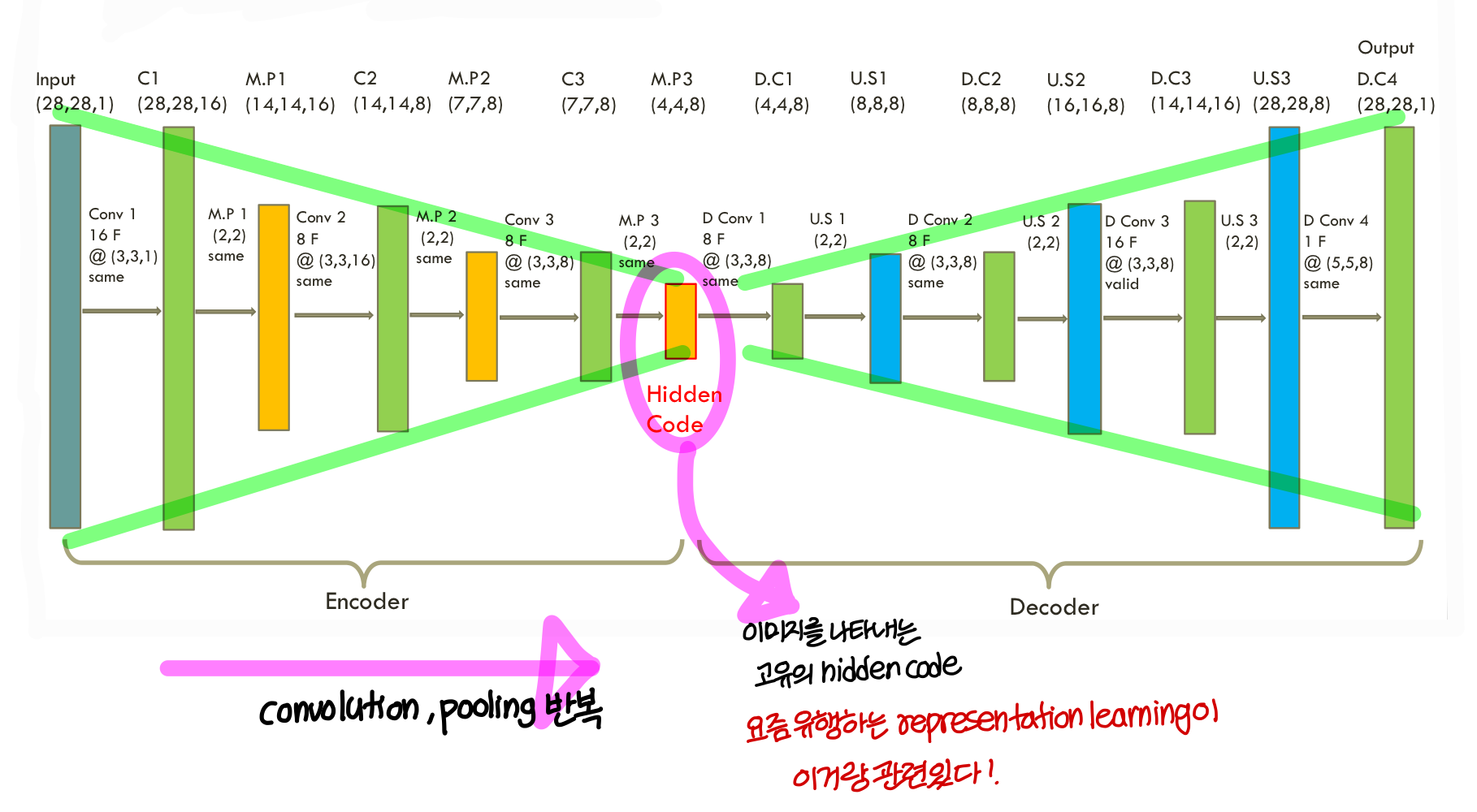
- representation learning
사람들이 영화 평점 매긴거를 토대로 추천 시스템을 만든다고 할 때
평점 매긴 영화 몇 개 안되니까 의미있는 데이터는 전체 데이터 중 아주 극 소수임
이런걸 가지고 학습하기가 힘드니까 이 데이터를 다음과 같이 정리하는거임
<영화 1 정보, 영화 2정보, 영화 3 정보, 영화 4 정보, 영화 5 정보.......>⇒<Action 영화 정보, Romance 영화 정보, SF 영화 정보...>→ 이런 식으로 만들고 학습하면 데이터가 잘 정리되어 있으니까 학습이 잘된다.

Regularization
- 의미 있는 Feature가 중간에 맺히게 하기 위해서는 regularization 과정이 필수
(overcomplete 이든, undercomplete 이든)
Sparsely regulated autoencoder
- Sparsely regulated autoencoder:
→ 우리가 원하는건 learned features들이 가능한 sparse 해지는거
→ sparse features로 우리는 generalize를 더 잘할 수 있음
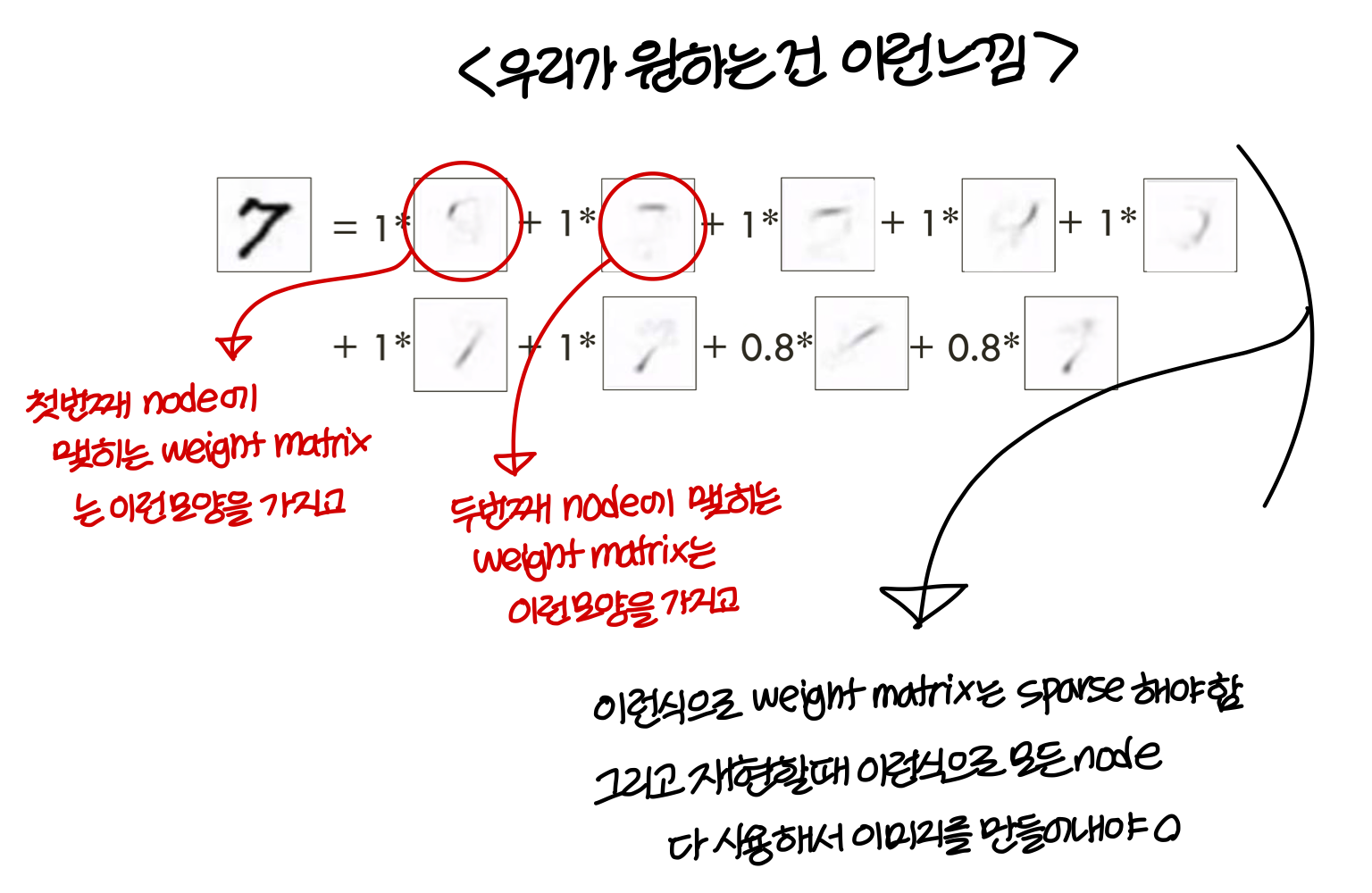
regularization 기본 아이디어

→ 앞에서 본 regularization 에서는 |w|가 무한정 커지지 않도록 하는거였음. 작아지는건 막지 않았음
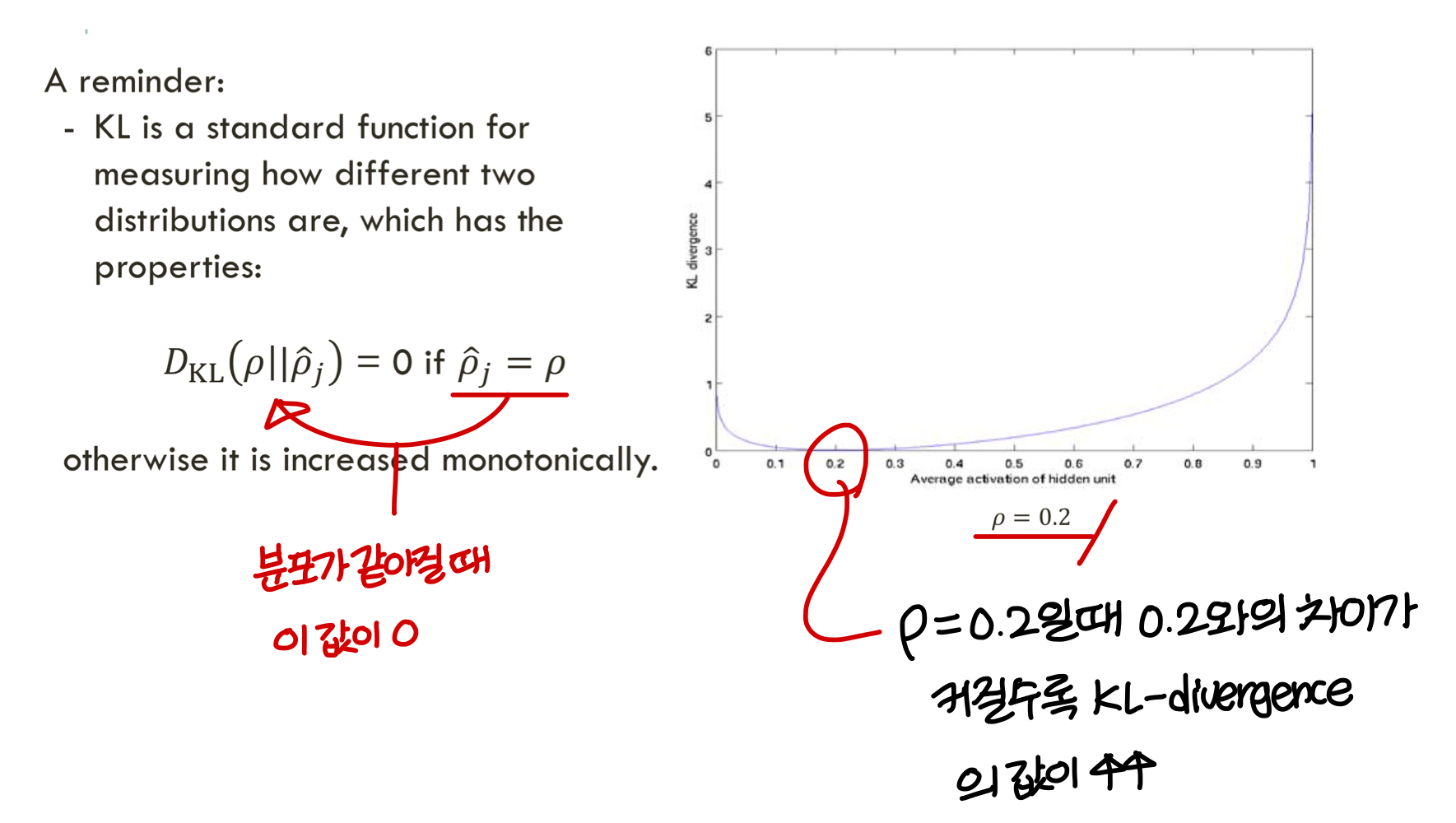
→ 여기서 하는 regularization은 무한정 작아지게 하는것도 안됨. 특정 값에 가까워지게 하는거임
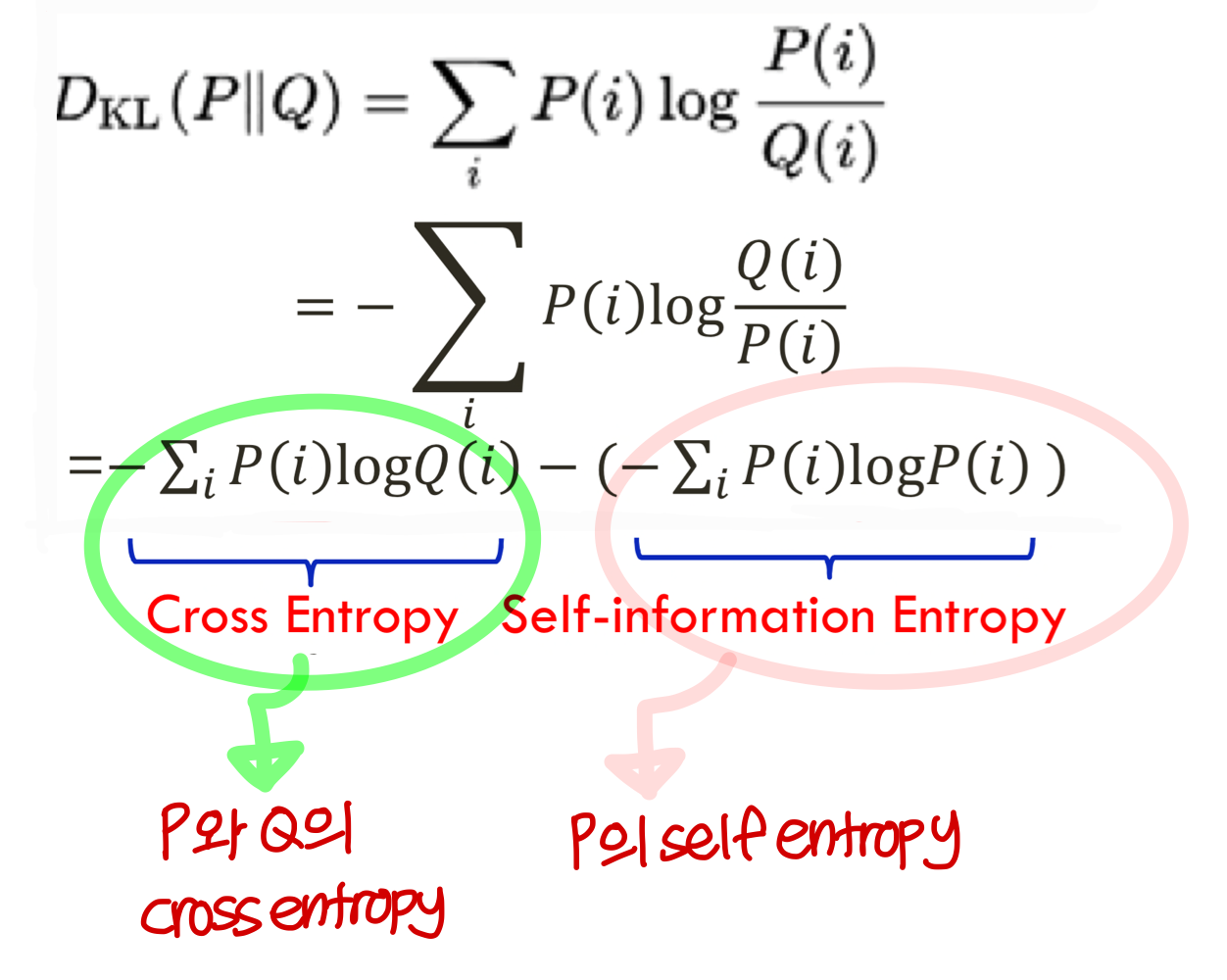
KL-divergence (Kullback-Leibler divergence)
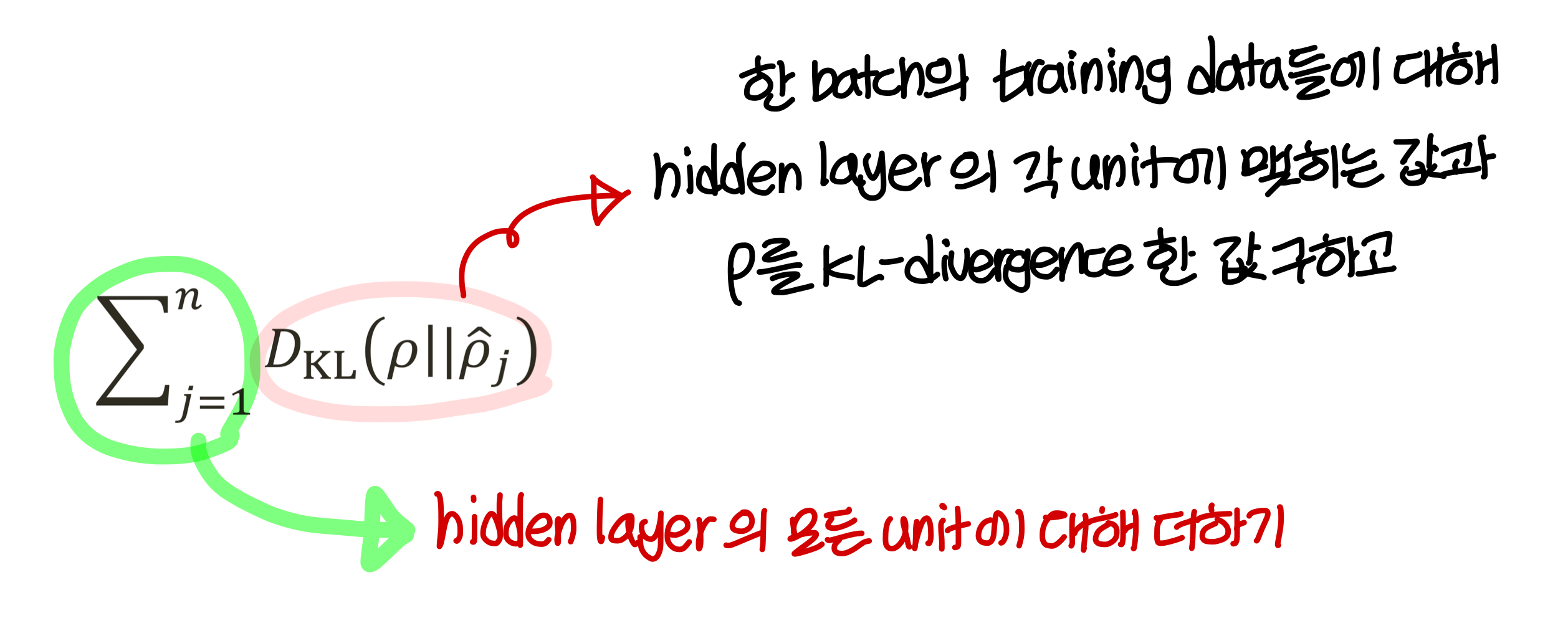
Cost function
Denoising autoencoder
- 아주 많이 쓰이는 autoencoder
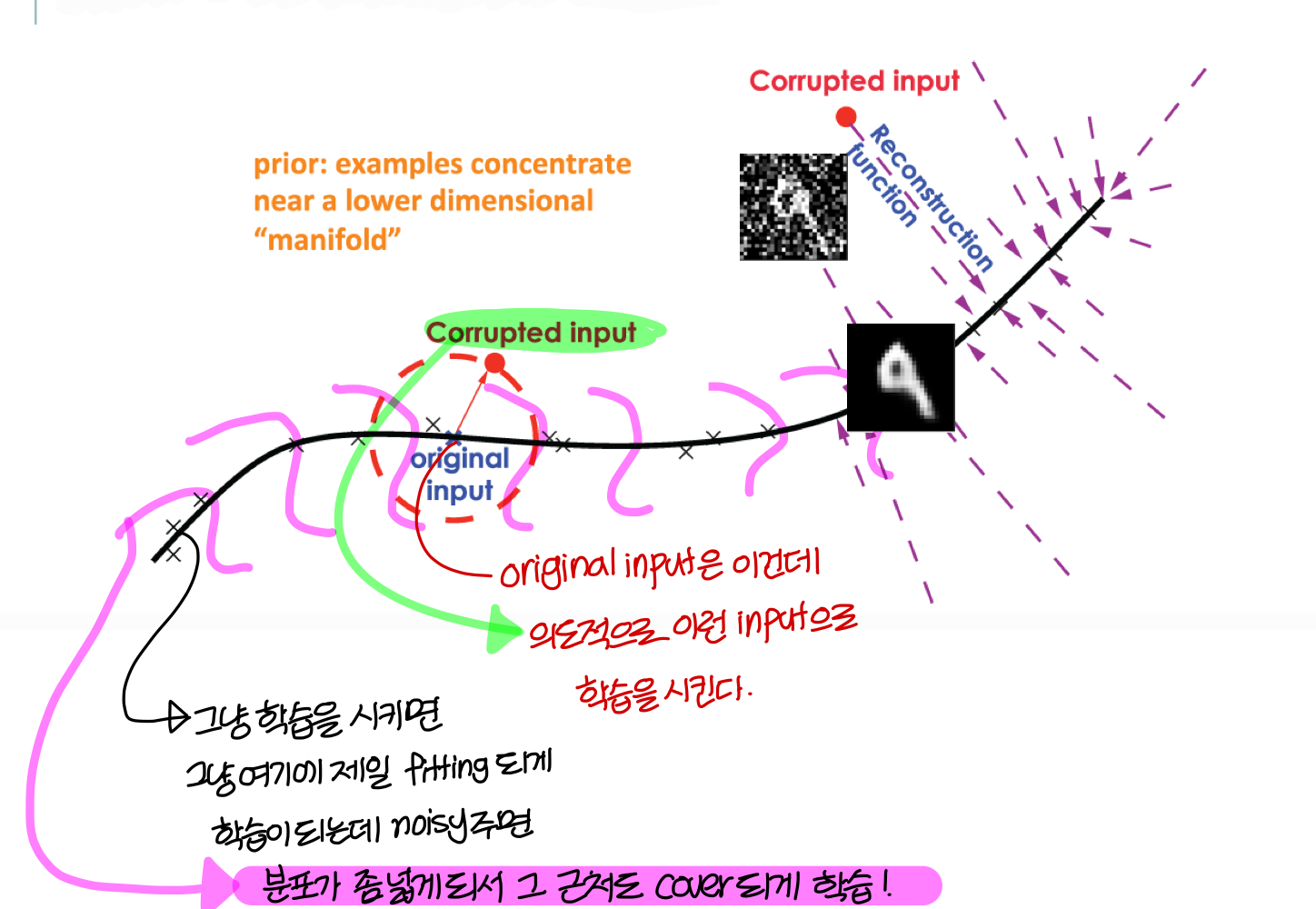
- 원래 training data에 일부러 random하게 noise를 주고 그걸 input으로 넣어줌
- 결과는 원래의 깨끗한 이미지 나오도록 학습시킴
- 더
robust model을 만든다고 보면 된다!
- noisy 준걸 다시 원상복구 잘함.
그럼 빵꾸 낸것도 복원해주나? → 얼추 비슷하게 복원해준다!
- 근데 이것도 data가 뭔지 보고 적용해야함
언어처리 같은거 할 때 denoising하면 X
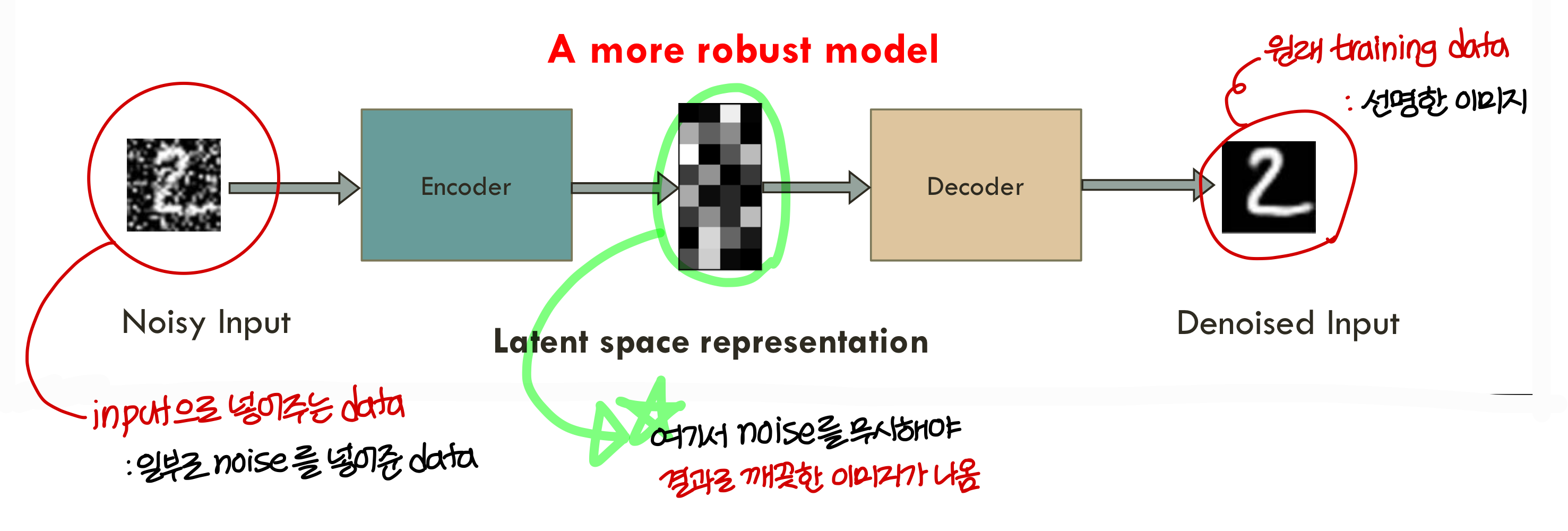

<그림으로 좀 직관적으로 표현해보자!>
Semisupervised learning using (denoising) autoencoders
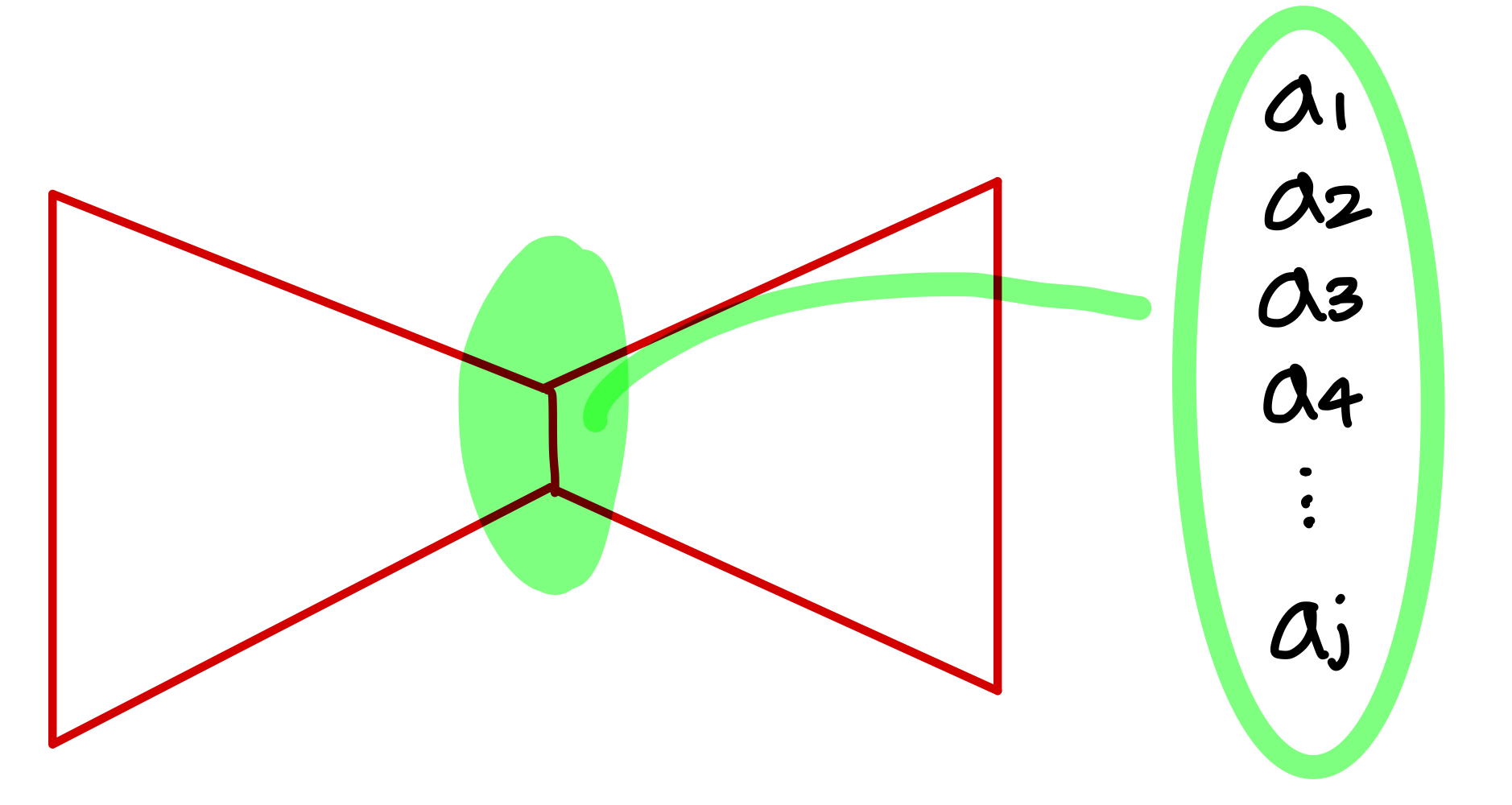
- autoencoder를 학습시켜서서 encoder 부분만 떼와서 latent space representation을 얻어낸 다음
그 뒤에 deep neural net을 연결함
- latent space representation는 꼭 필요한 feature vector만 가지고 있음
한쪽은 unsupervised learning,한쪽은 supervised learning이라서 ⇒ semisupervised learning이라고 부름!
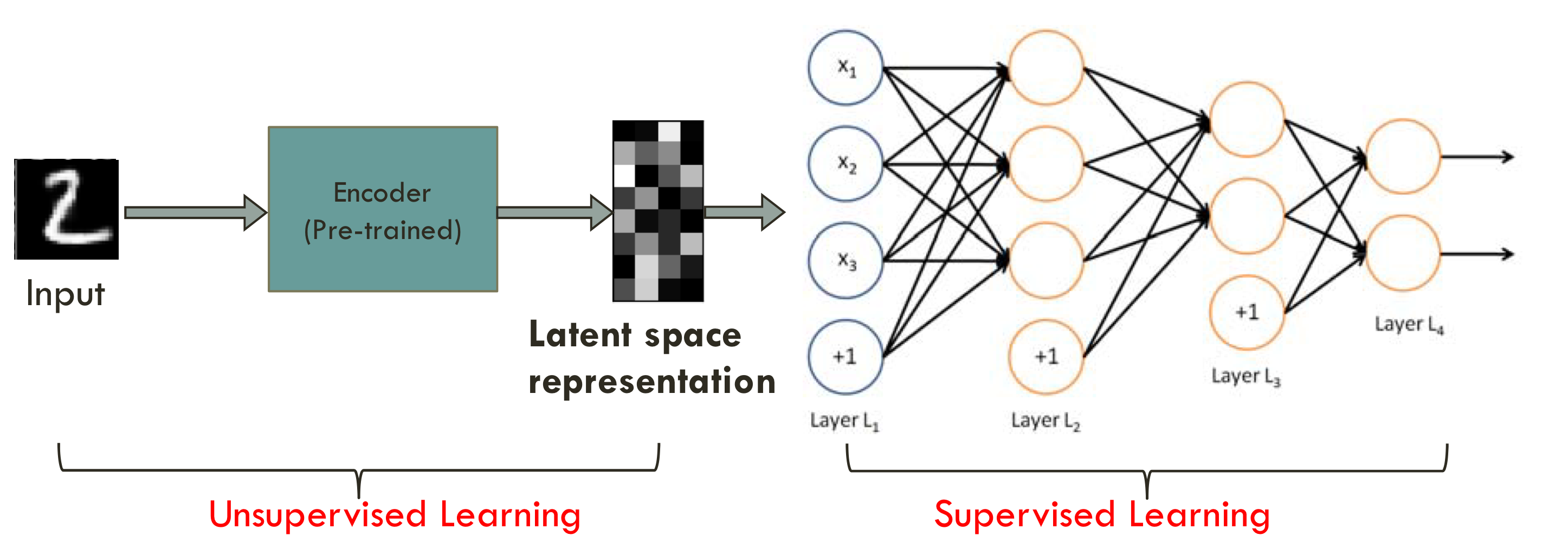
- 100만개의 데이터가 있는개 2만개만 labeling이 되어있음
<semisupervised learning을 한다면>앞 부분은 100만개의 데이터로 학습을 하고
뒷 부분은 2만개로 학습을 함
<seimisupervised learning을 하지 않는다면>2만 개의 데이터로만 학습
⇒ semisupervised learning을 할 때가 더 성능이 좋음, labeling 인력도 줄어서 좋고
⇒ 그래서 semisupervised를 하는게 더 일반적인 방법임
Stacked AE
- 지금 auto encoder에 hidden layer 한층만 있는거만 살펴봄
- stacked AE는 auto encoder를 여러층으로 붙여준거
- 성능 향상 위해 deep neural net이 필요할 때 stacked AE를 쓸 수 있음
Stacked AE - train process
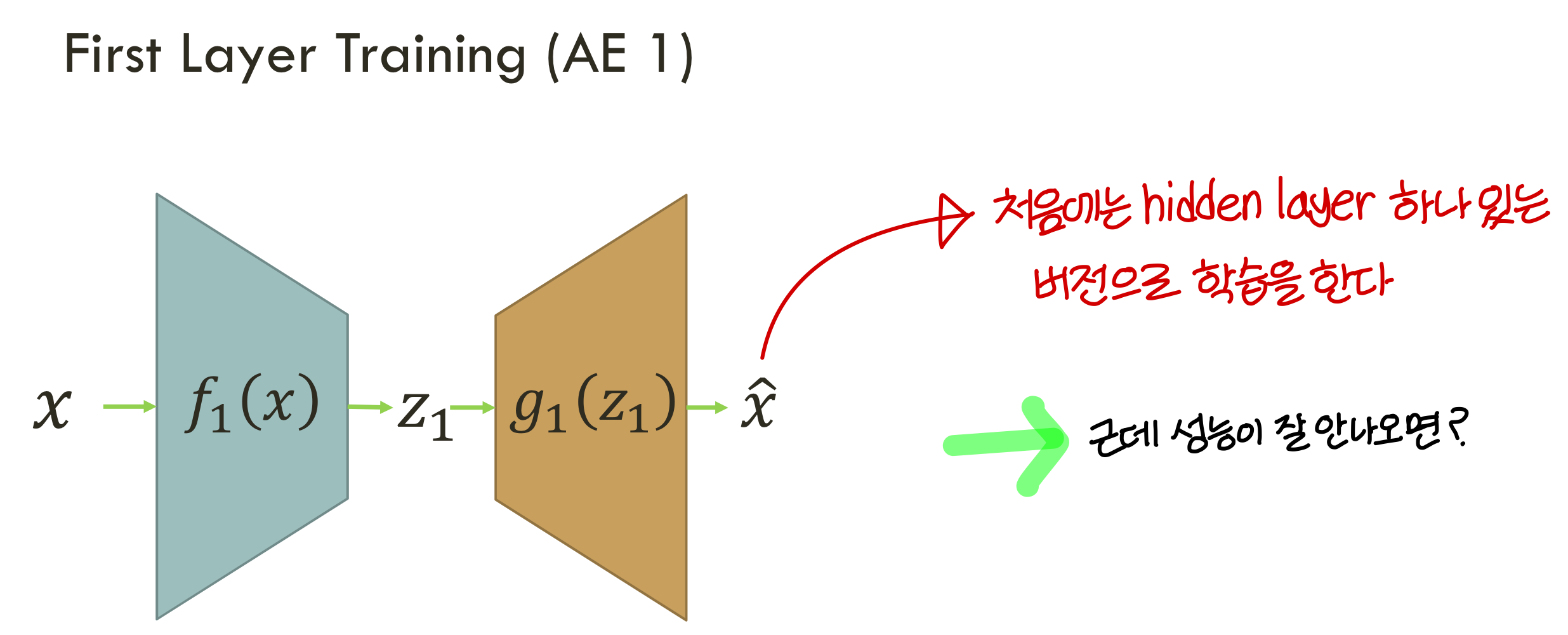
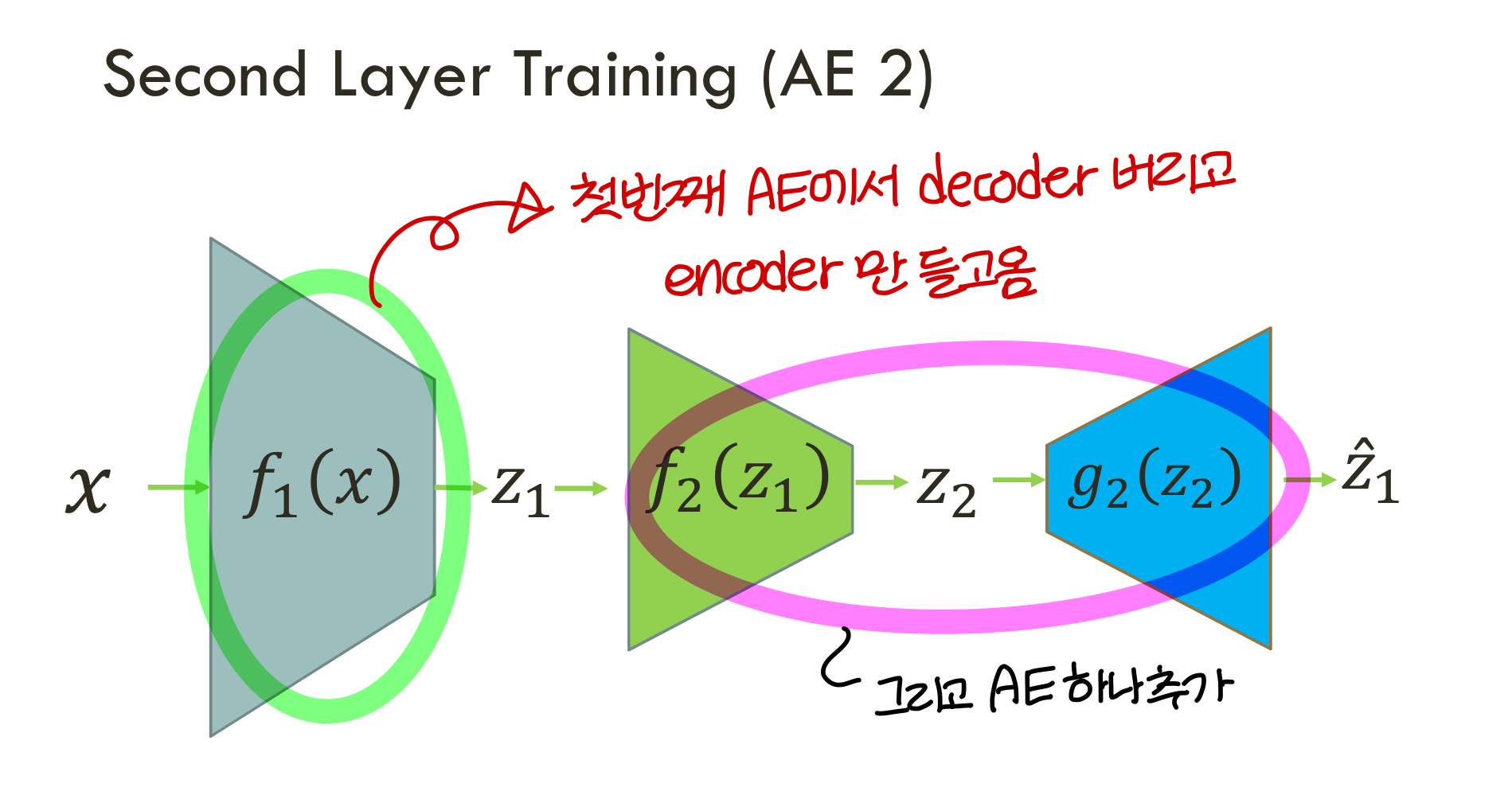
- 그리고
stacked encoder를 앞에서봤던것처럼 semisupervised learning에 사용하는게 일반적
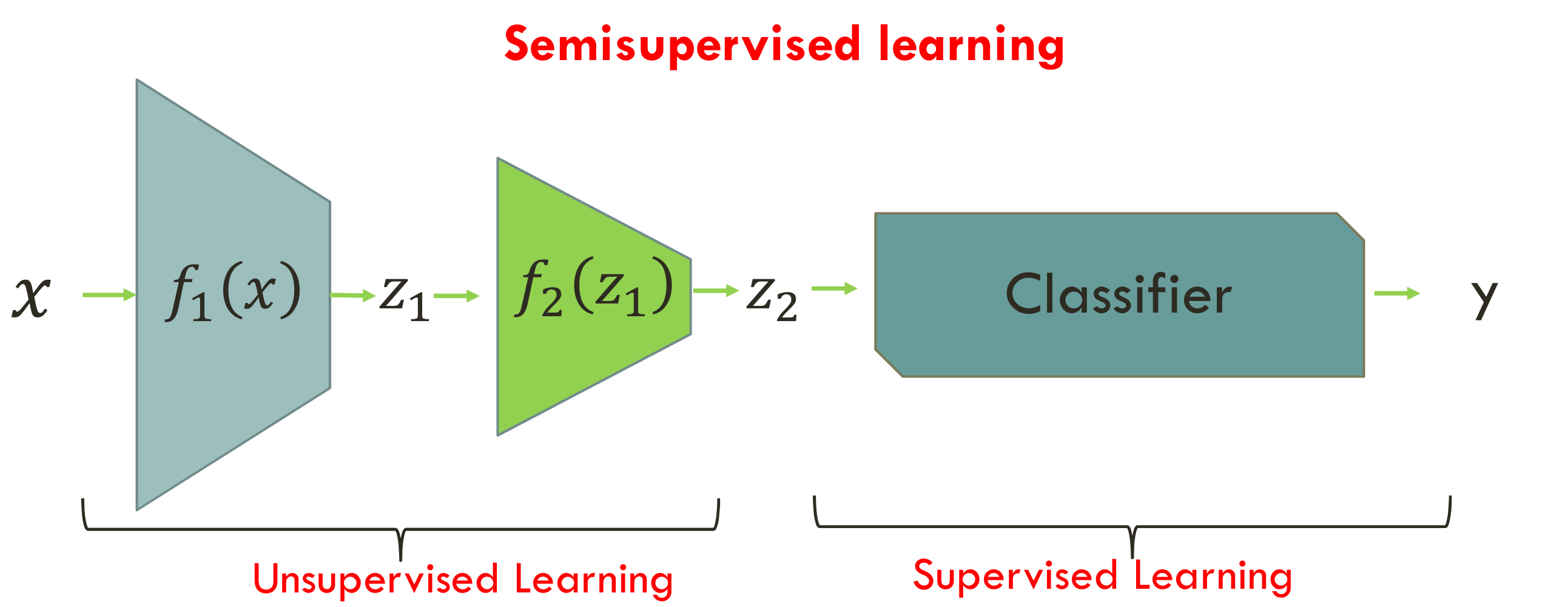
Contractive autoencoders
- 우리 uninteresting feature 피하는데 여전히 관심있음!
→ 앞에서 hidden layer를 limit시키기 위해 regularization term을 loss function에 추가했었음
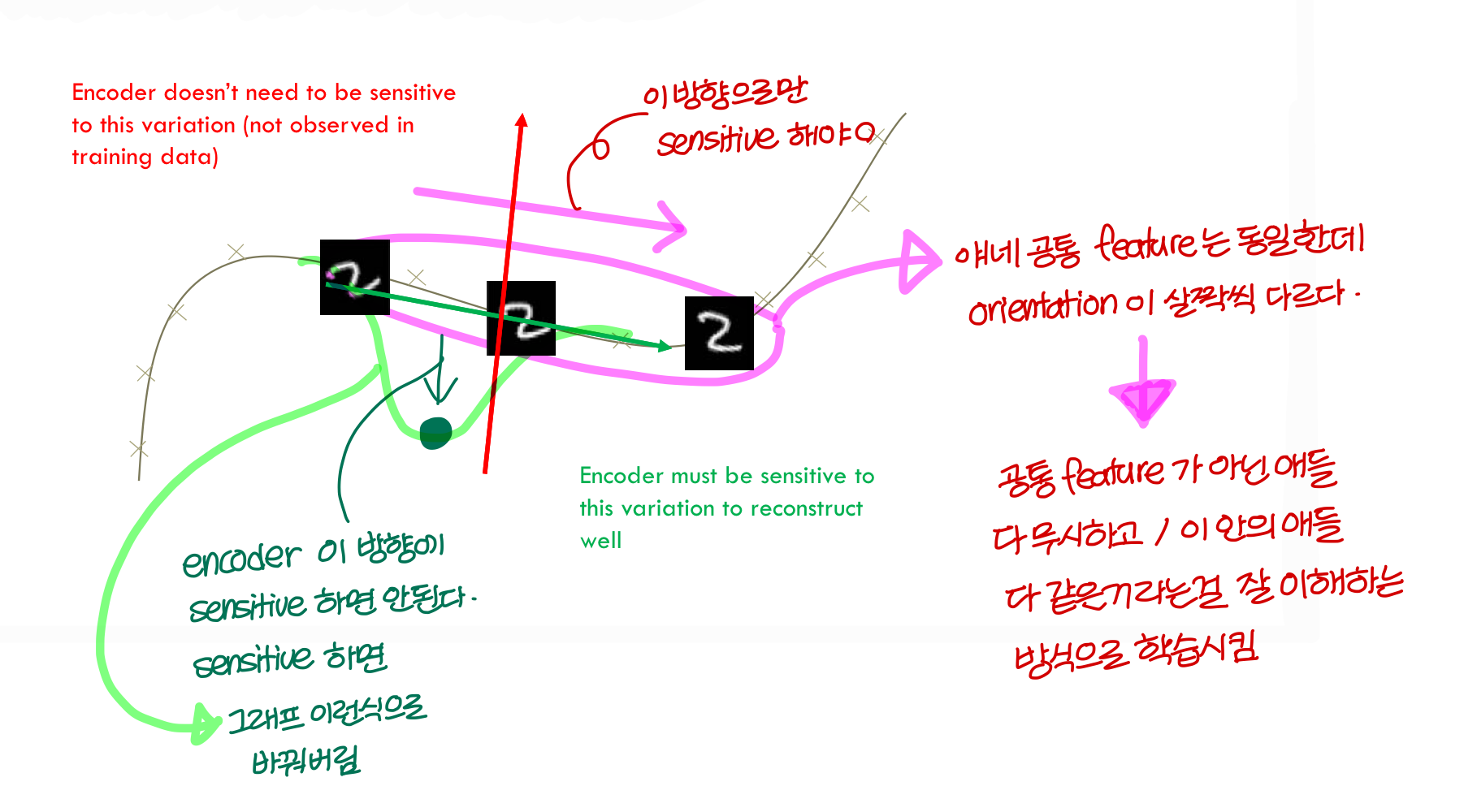
contractive AE의 아이디어:training set에서 관찰되는 variantion만 반영하는 feature를 추출하고 싶다!
다른 변화에 대해서는 invariant하게 만들고 싶음.
그리고 input space에서 가까운 point끼리 latent space에서 property를 유지하게 하고 싶음
말이 뭔가 어려운데 중요한 feature에 대해서는 민감하게 반응하고, 중요하지 않은 feature에 대해서는 둔감하게 반응하도록
feature vector의 variation을 작게 만든다고 이해하면 될듯
Definition and reminders
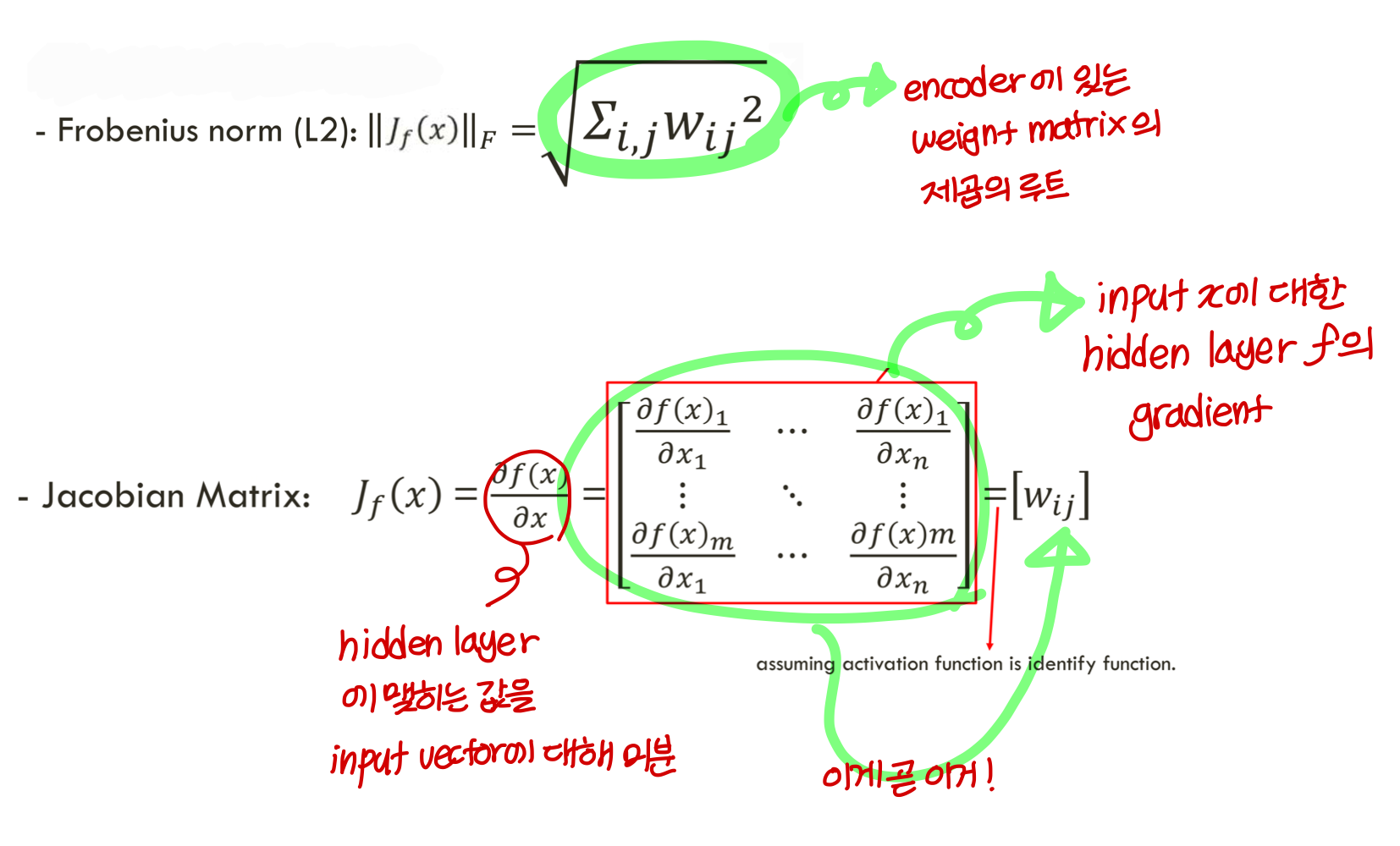
- 그래서 우리의 새로운 loss function은 다음과 같이 구성됨
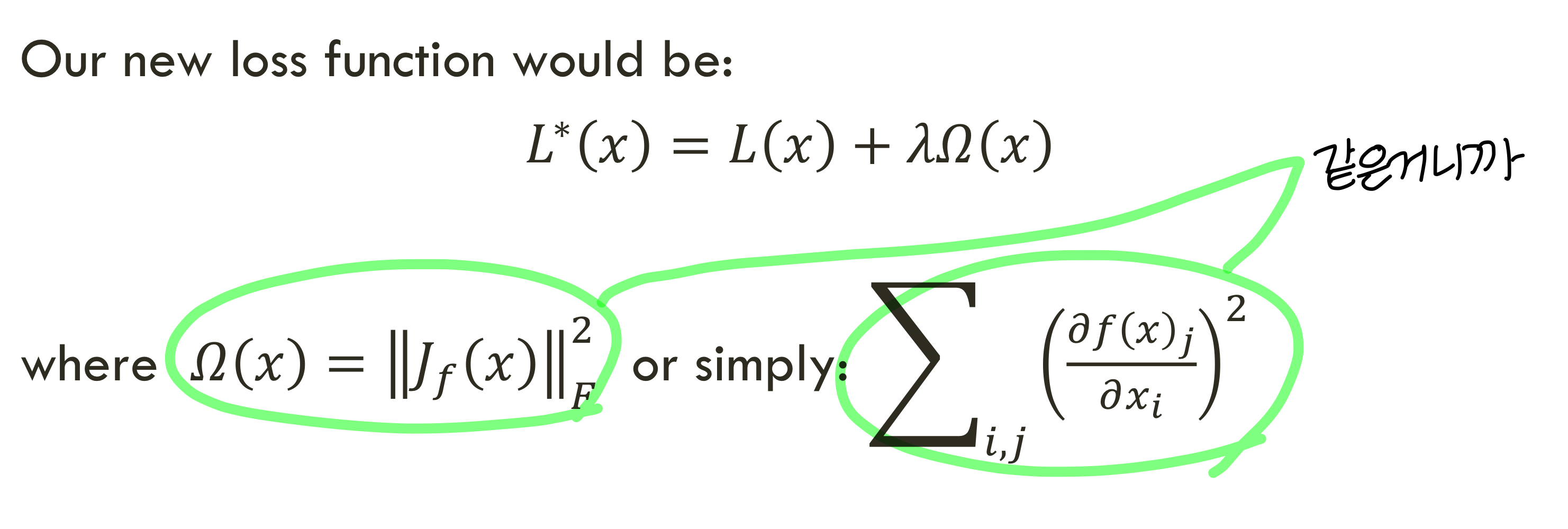
→ 이때 λ가 0에 가까워지면 loss function으로 그냥 cross entropy만 쓰는거
: 이러면 training data 각각에 대한 loss만 최소로 만들고
variation을 잘 처리하지 못함
새로운 데이터를 잘 처리하지 못할수도도
→ 그럼 λ가 ∞에 가까워지면 loss function으로 그냥 Ω(x)만 쓰는거
이러면 training data에 대한 모든 정보를 잃게 될것
→ 지코비안이 x에 대해 미분하는건데 이걸 작게 유지한다는건?
: x가 변하더라도 결과 많이 변화하지 마라 이거지
→ variation을 작게 만든다!
→ regularization 효과!
<그림으로 좀 직관적으로 표현해보자!>
Which AutoEncoder?
- DAE는 입력 데이터에 랜덤한 노이즈를 추가하여 입력의 작은 변화에도 강건한 모델을 만드는게 목적
- CAE는 중요하지 않은 입력의 변화를 무시하도록 학습하는 것을 목적
⇒ DAE(denoting AutoEncoder)와 CAE(contractive AutoEncoder)는 서로 상호 보완적으로 잘 작동한다
Uploaded by N2T