딥러닝 수업정리) 03_Shallow Neural Network

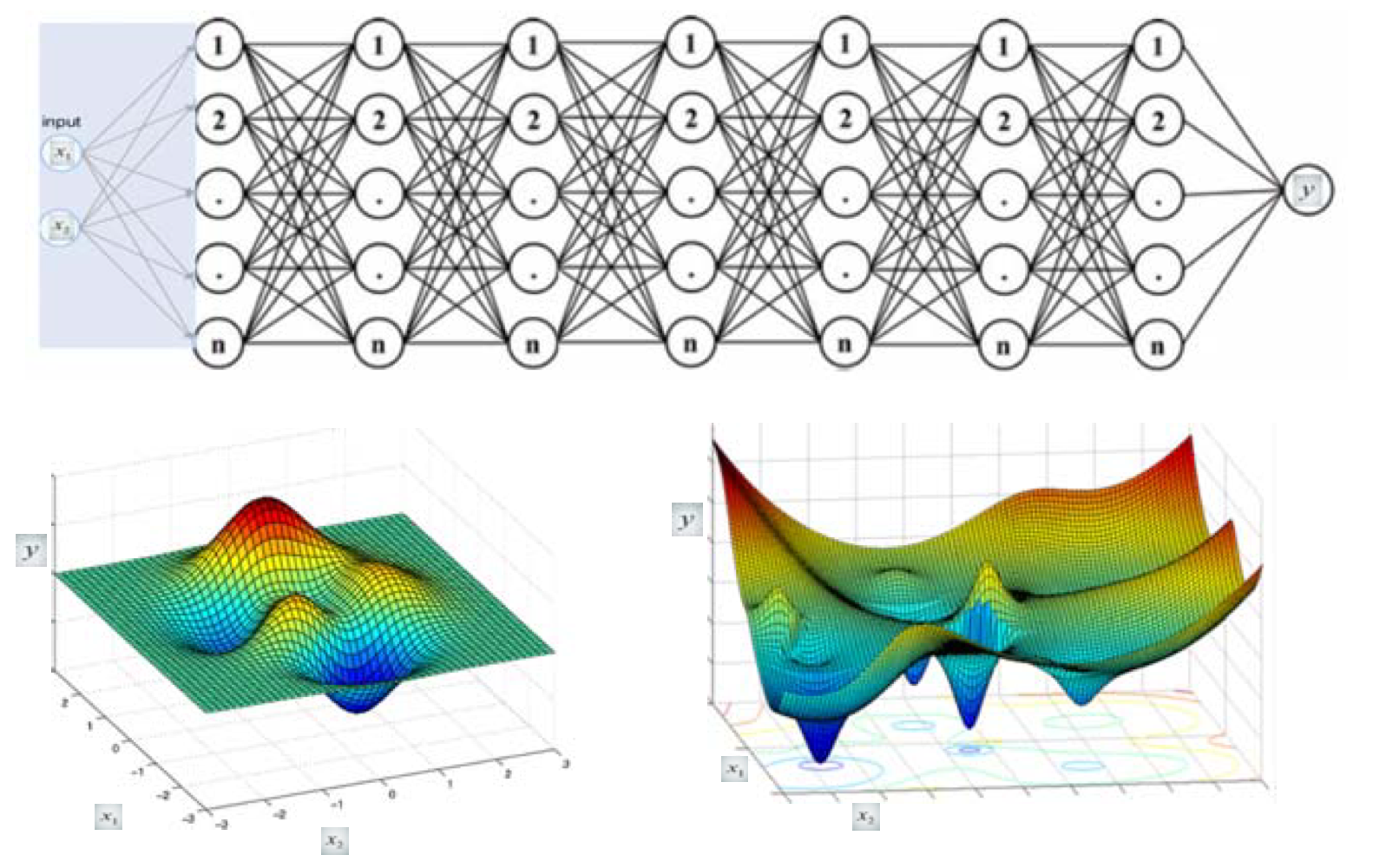
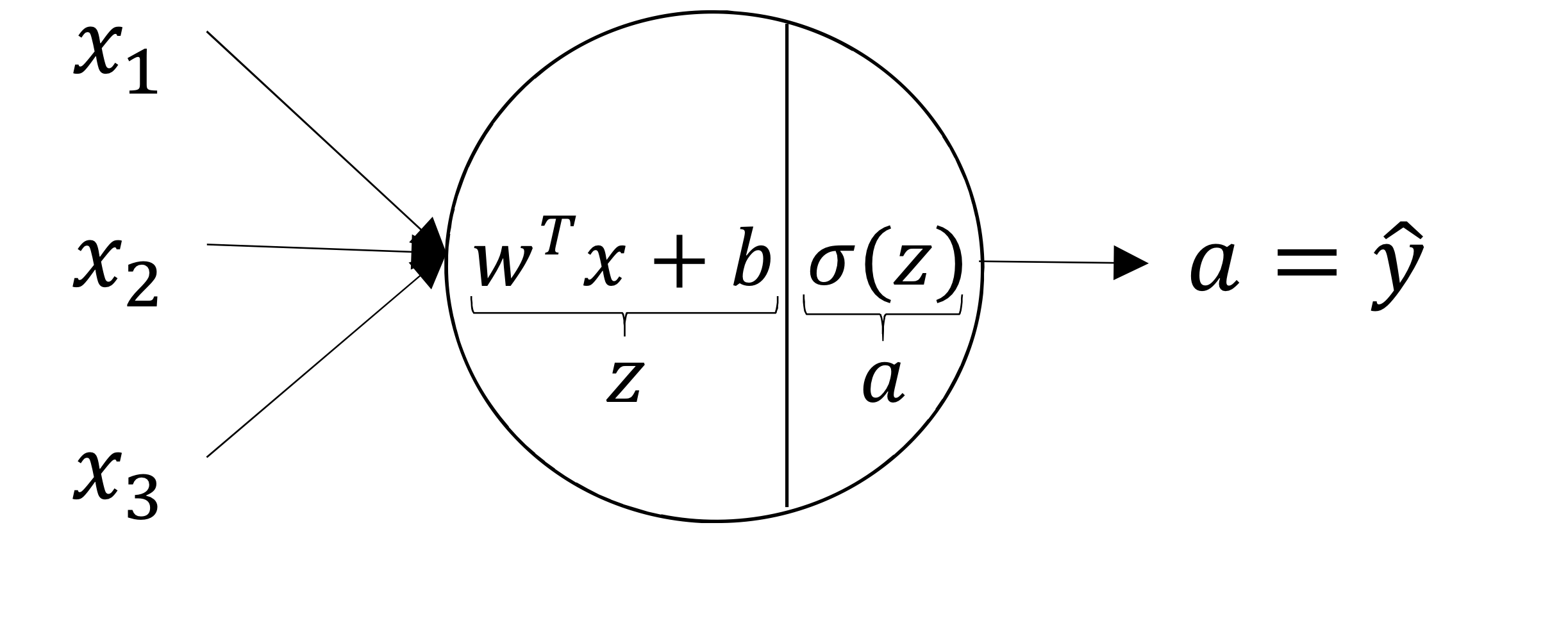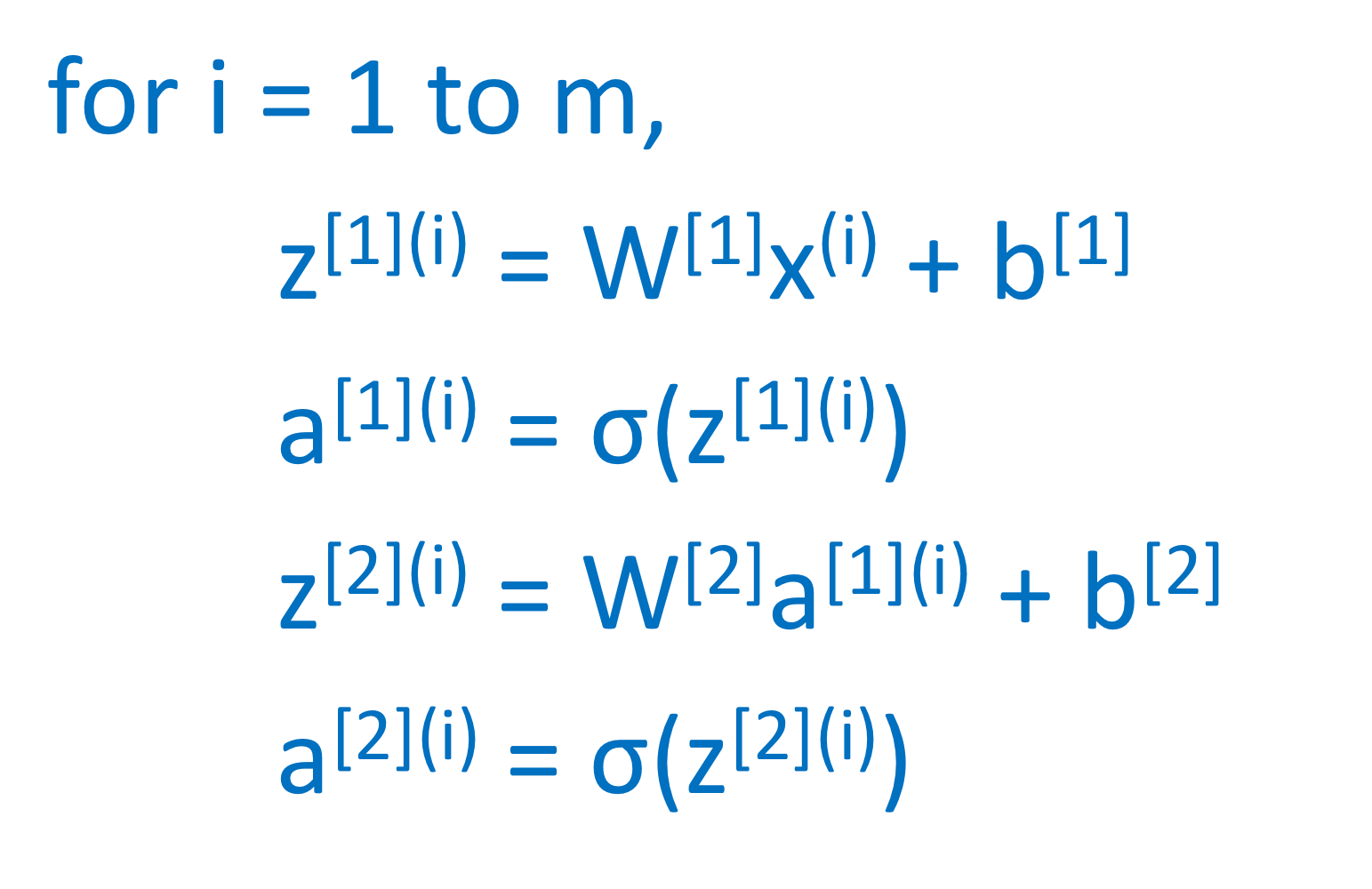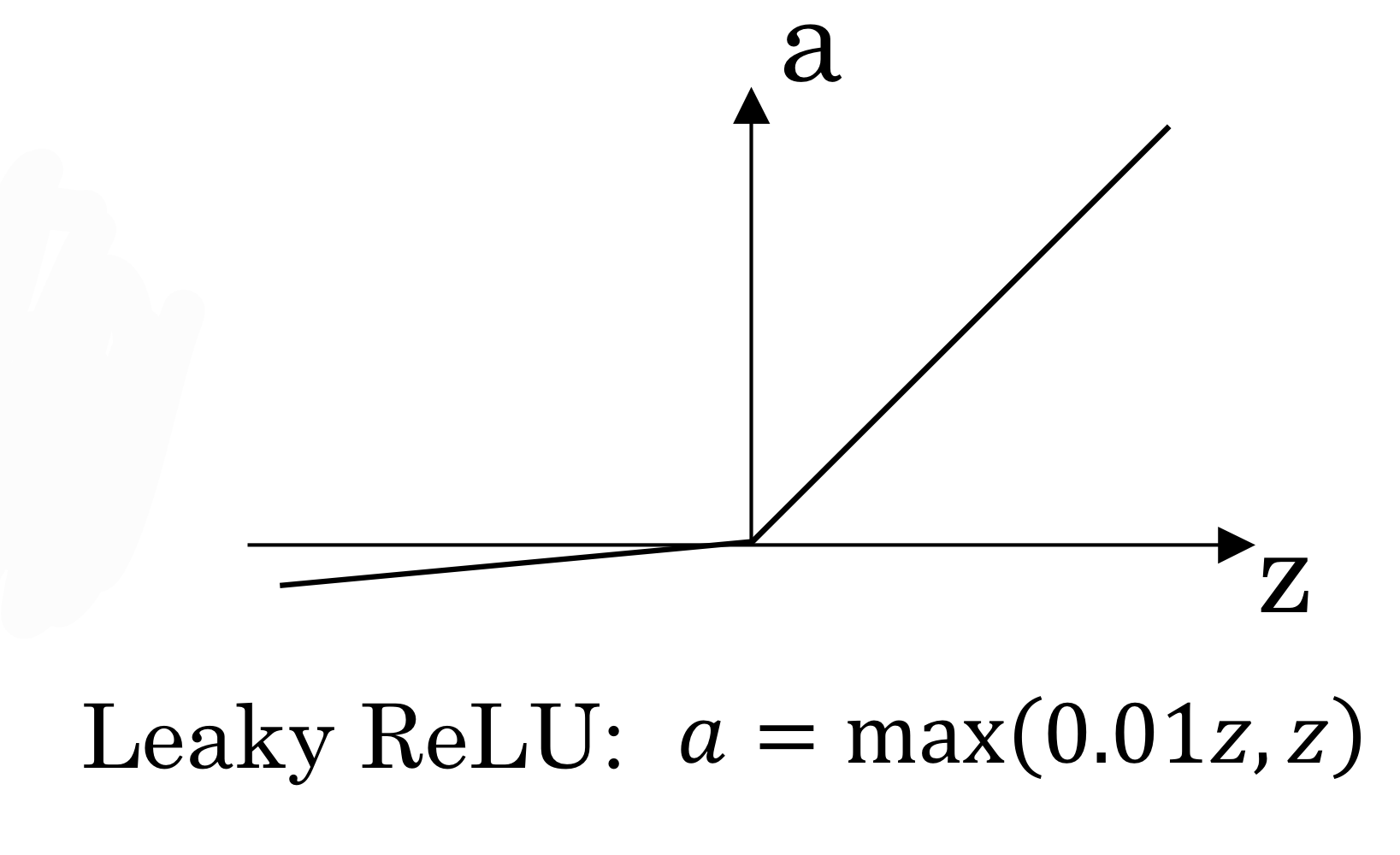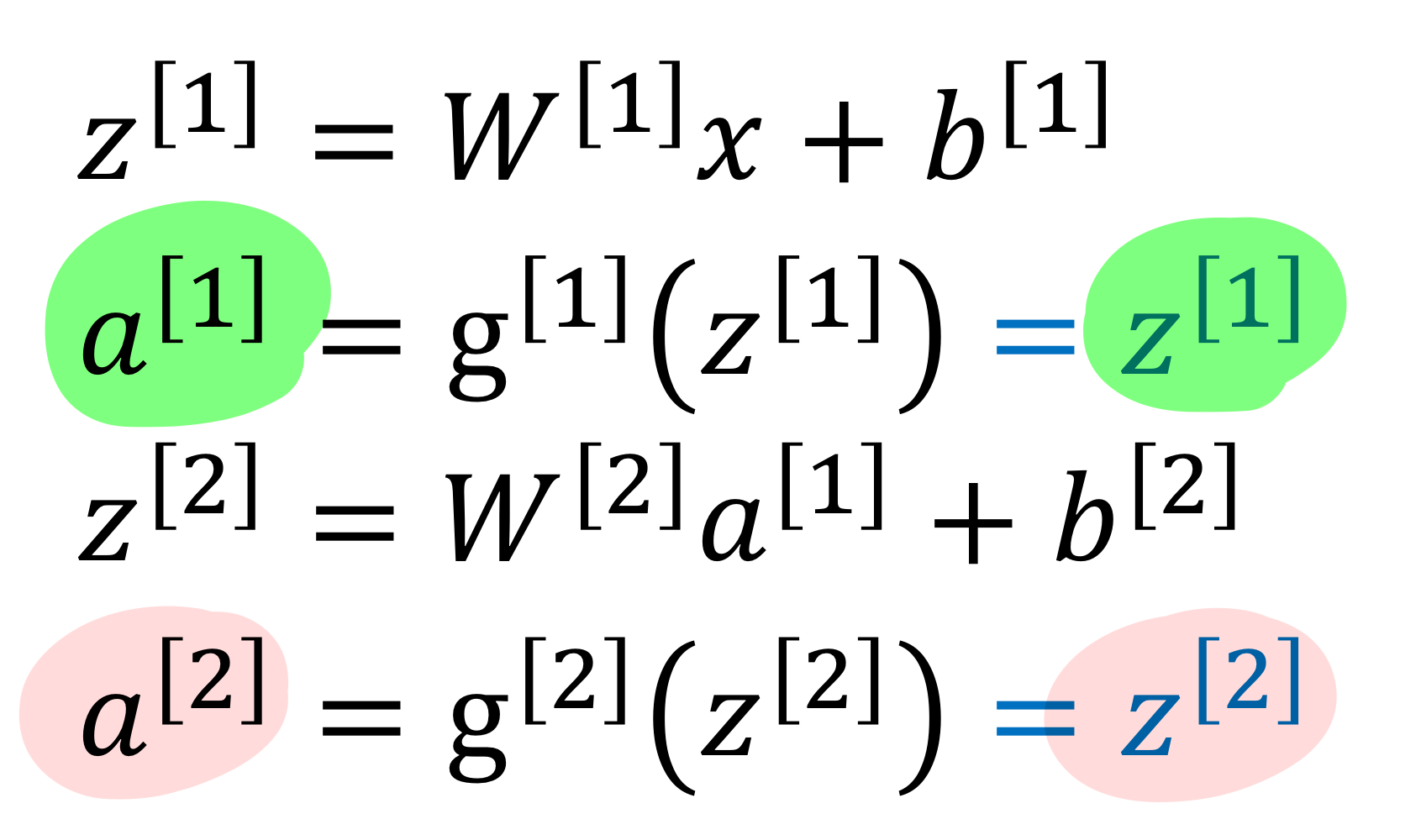• deep neural net을 배우기 전에 shallow neural net 먼저 배울거임

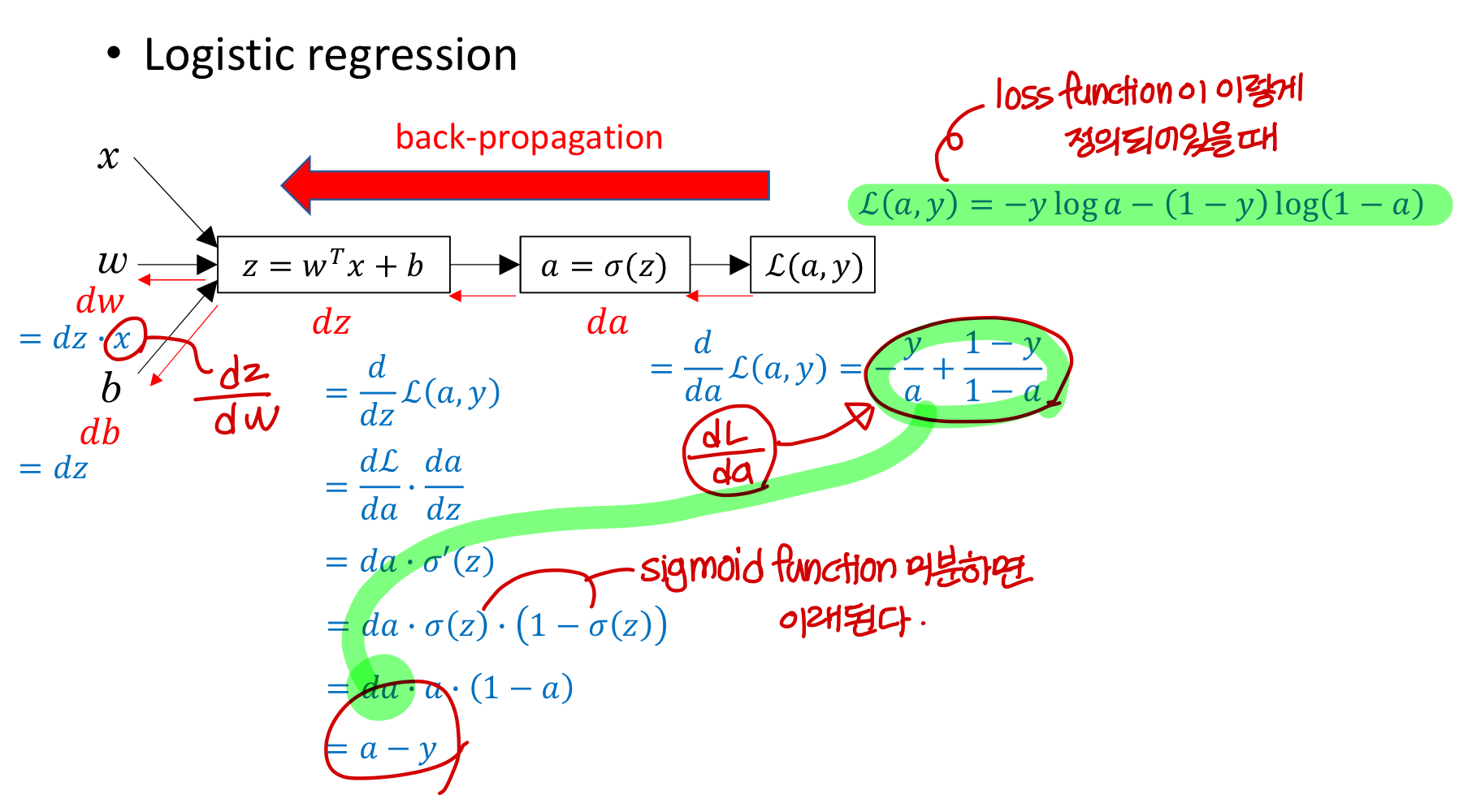
What is Neural Network

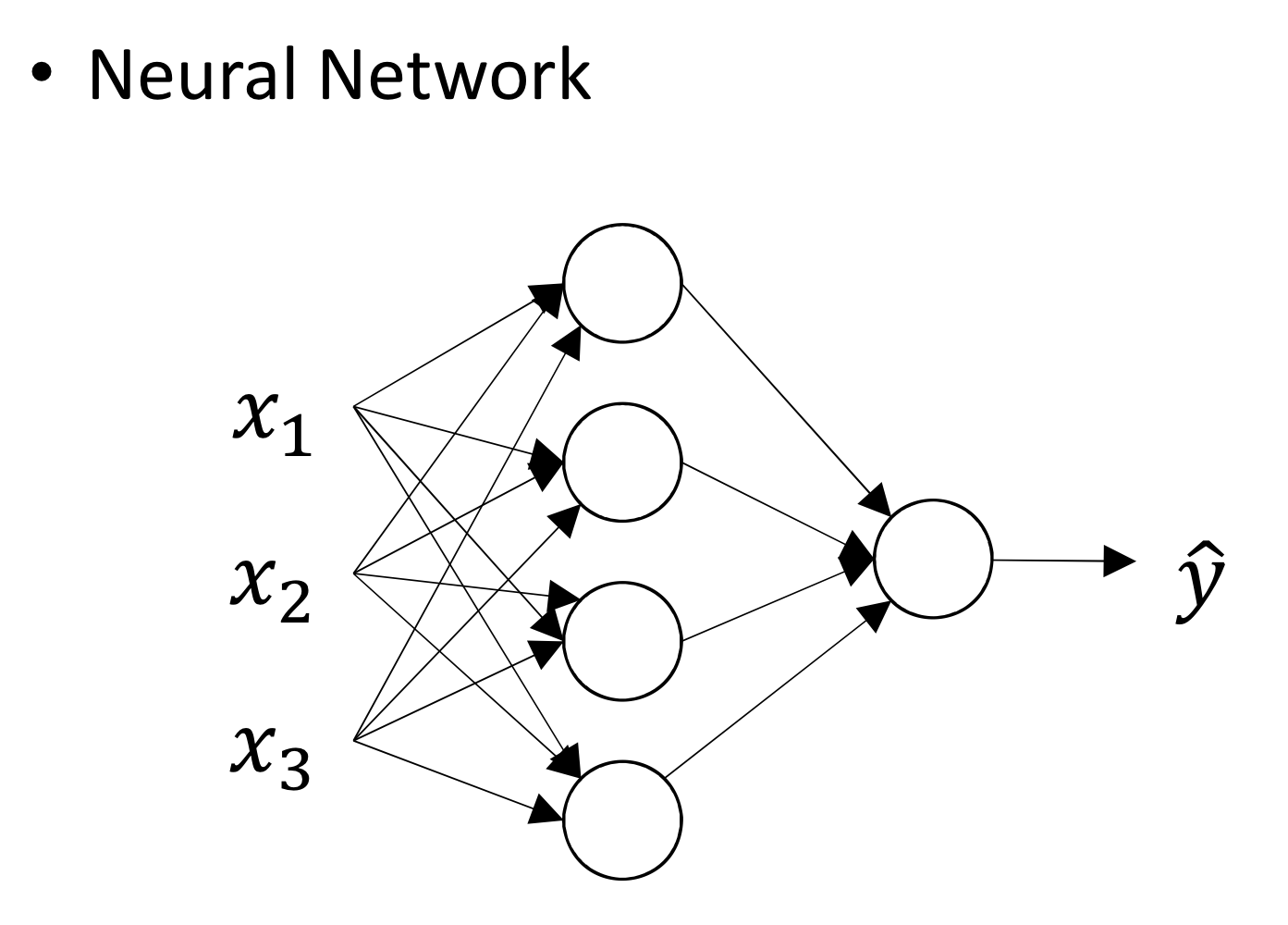
• 이제 뉴런 하나 쓰는게 아니라 뉴런 4개 쓰고 있음

• 총 4개의 logistic regression이 2개의 layer로 연결된 상태

  

---

• 표기에서 [i] → 이건 i 번째 layer 의미

  표기에서 (i) → 이건 i 번째 training data라는 의미

• training data가 $<(x_1, x_2,x_3), y>$ 이런식으로 주어질거임

• computation graph로 나타내면

  

Neural Network Representation

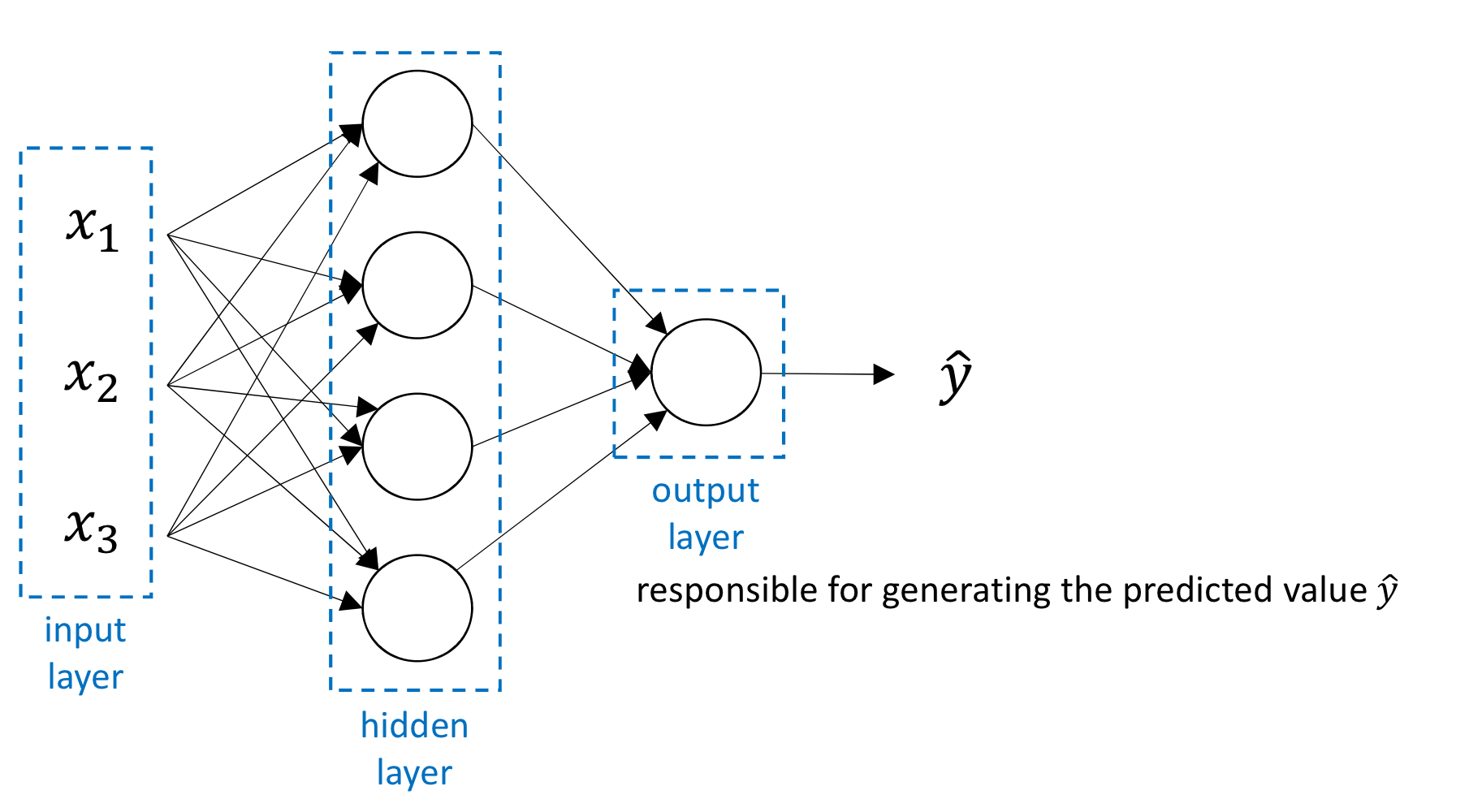
• training data는 Input layer의 값과 output layer의 값으로 주어짐

• 근데 중간 layer의 값은 실제로 값을 넣어봐야 나오는거기 때문에

  training data에서 값을 명시적으로 주지 X

  그래서 이 부분을 hidden layer라고 부름

• layer가 늘어날 때, input layer와 output layer의 빼고 그 사이의 layer는 전부 hidden layer

---

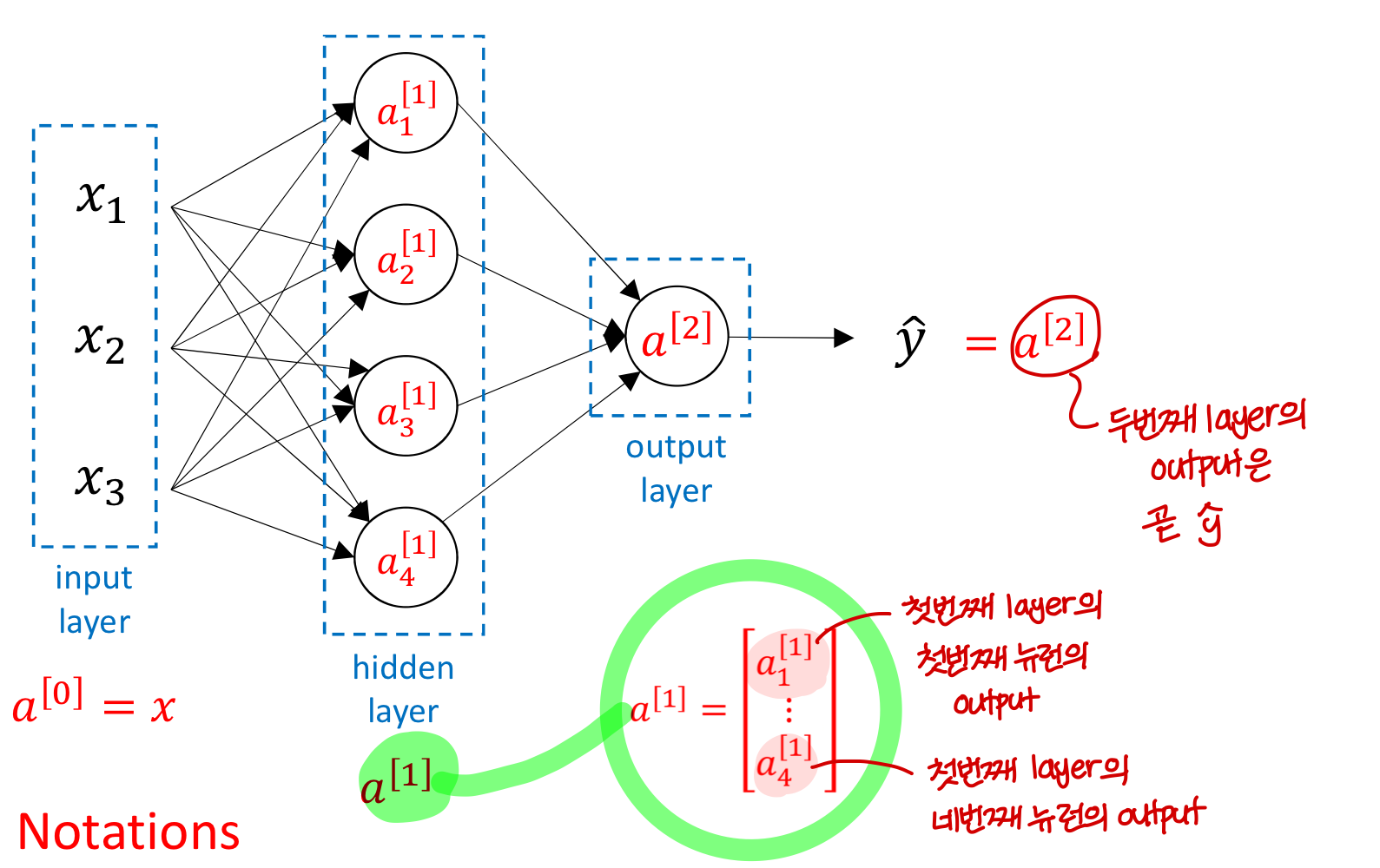
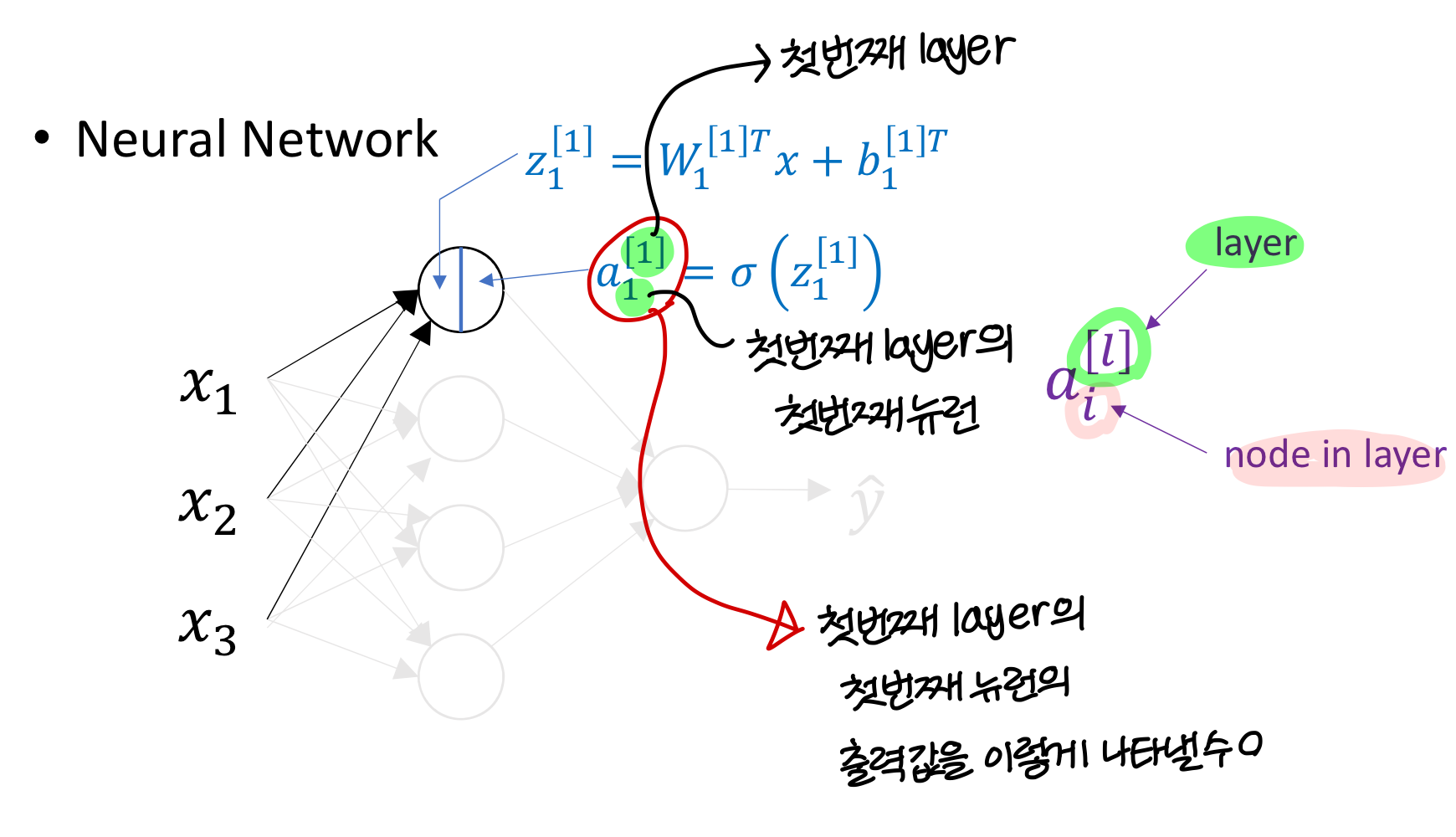
• 앞선 챕터에서 output 즉 y hat 값을 a라고 표현했었음

  💡

  이제 input $x$를 Input layer의 출력값으로 보고 $a^{[0]}$라고 부를거임

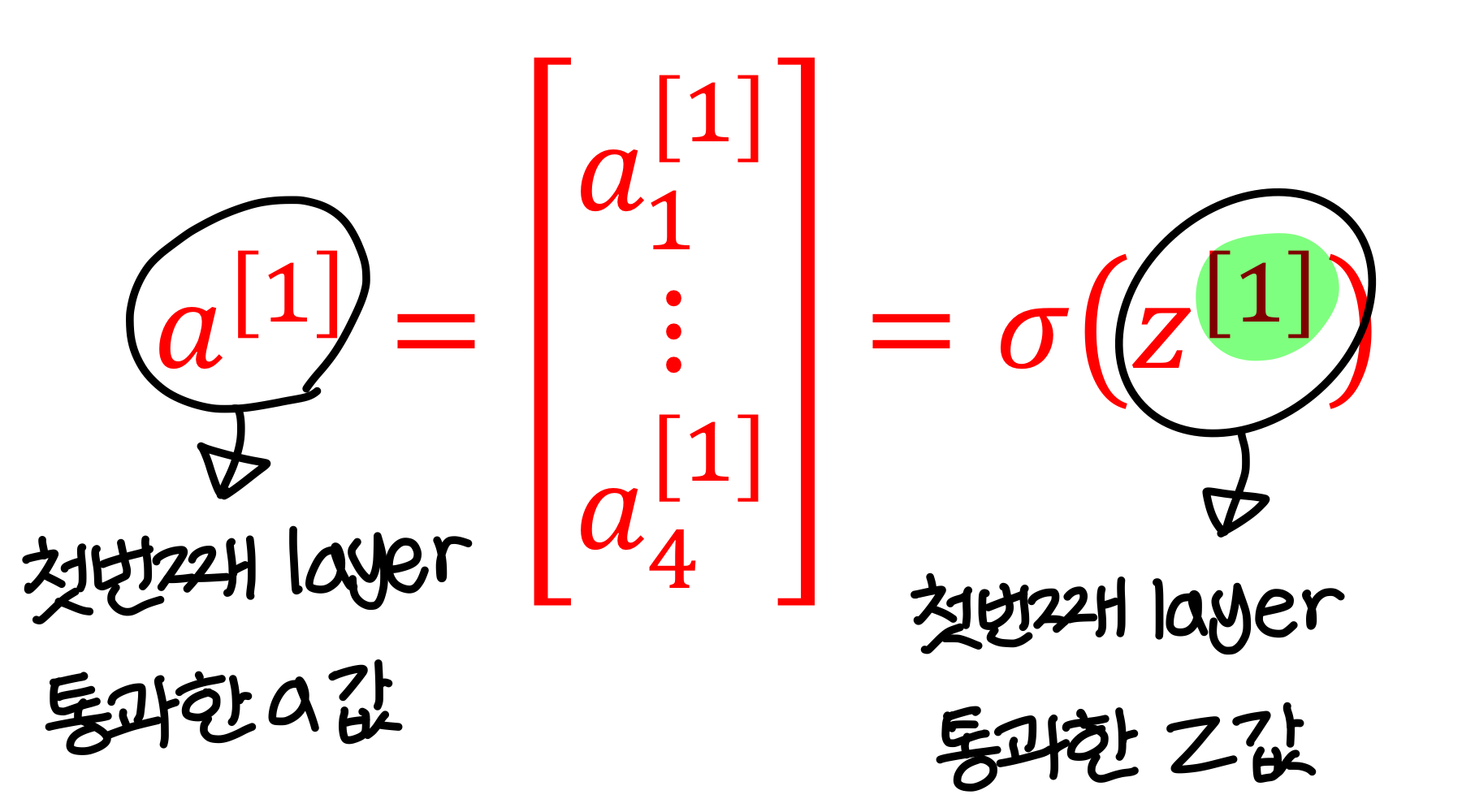
→ 마찬가지로 첫번째 layer의 output을 $a^{[1]}$

---

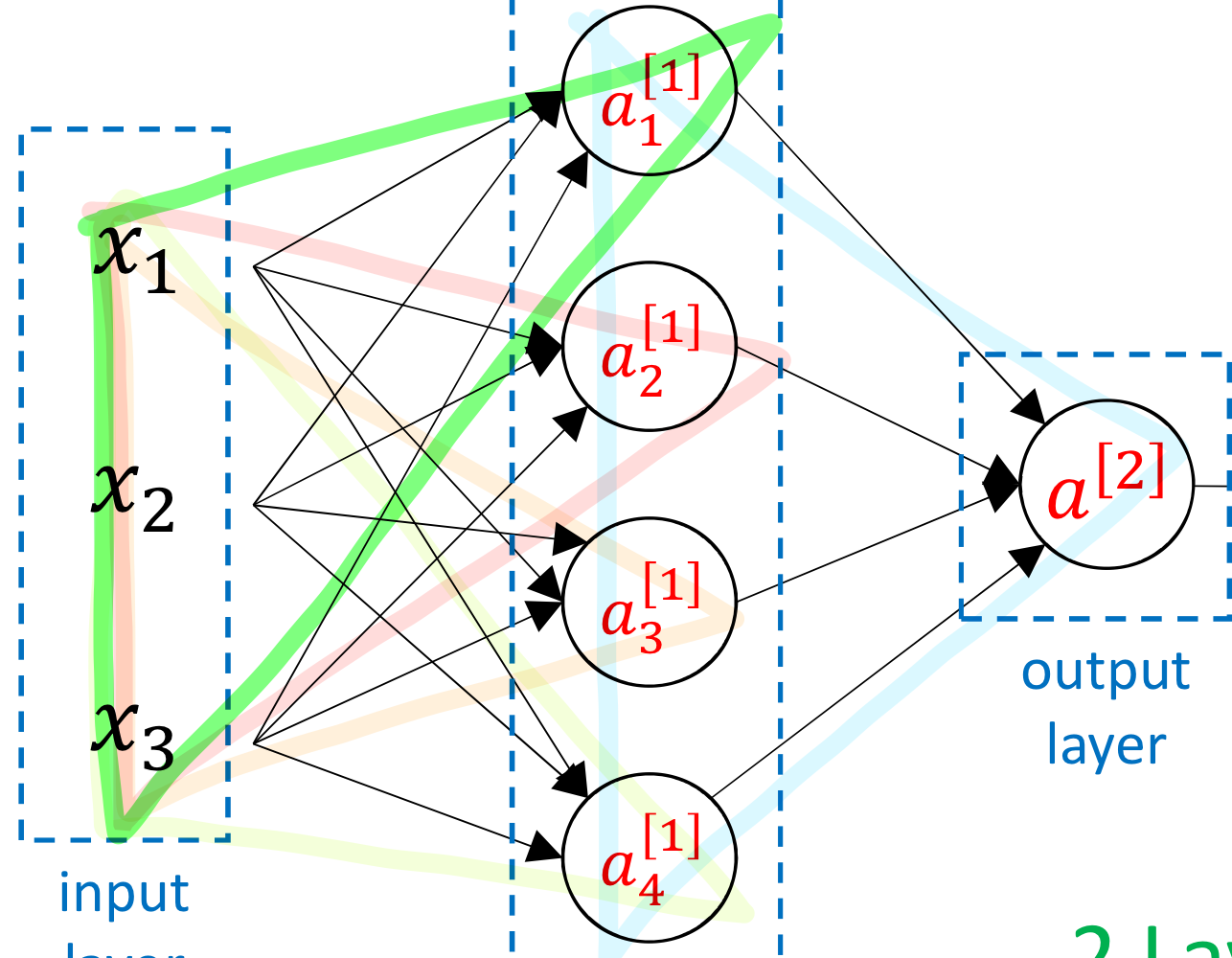
• layer 셀 때 input layer는 세지 X

  (즉 위의 neural network는 2 layer neural network)

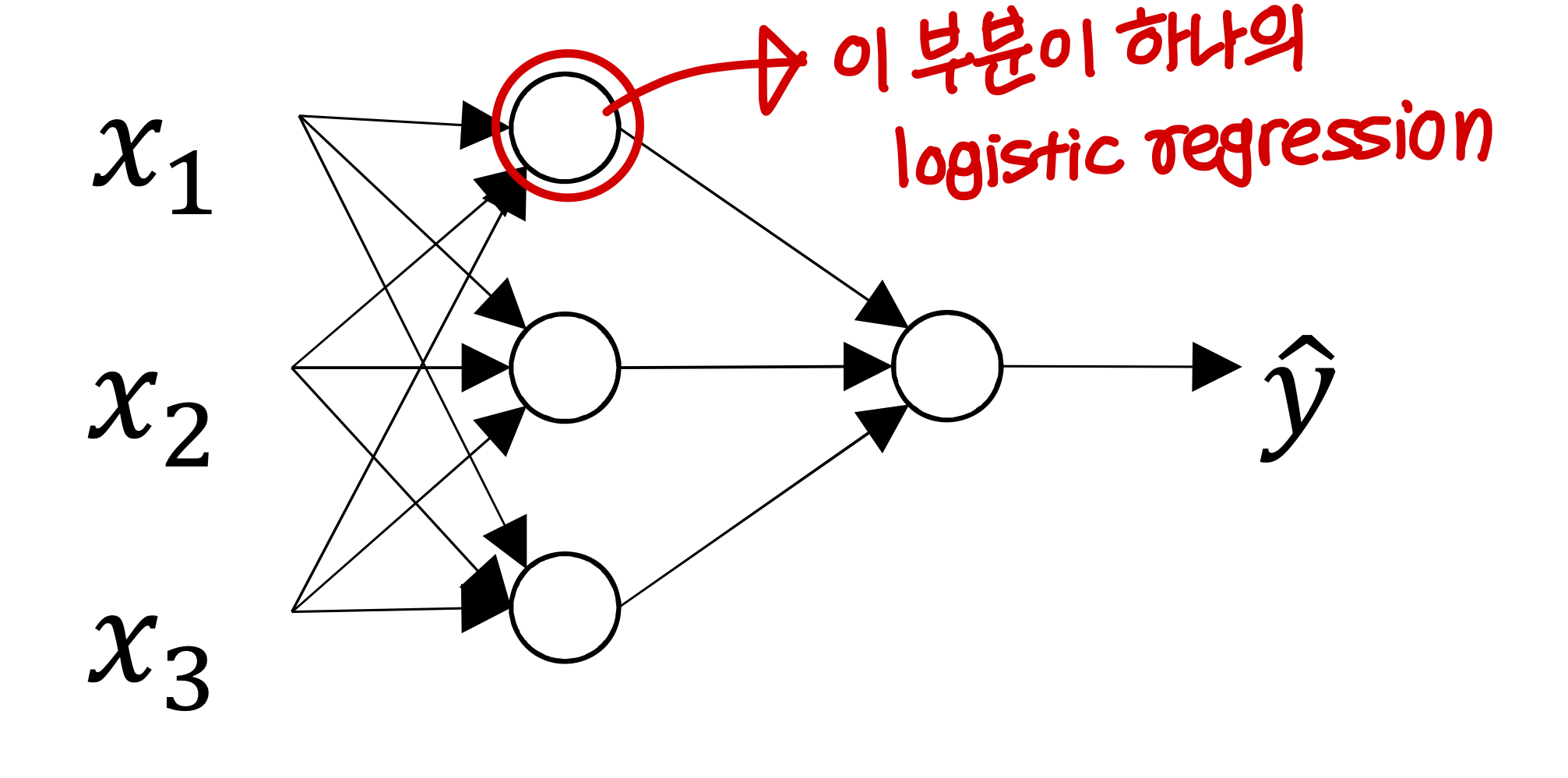
  logistic regression이 하나의 뉴런을 의미하기 때문에 뉴런을 이런식으로 개수 센다

  

---

• 그리고 앞전에도 언급했지만 Input layer에 가상의 input $x_0 = 1$이 있다고 생각하면 됨

  → 그러면 matrix 연산이 깔끔하게 되기 때문!

  → 실제 training data에 $x_0 = 1$이 포함된다는건 아님

---

• weight의 크기

  

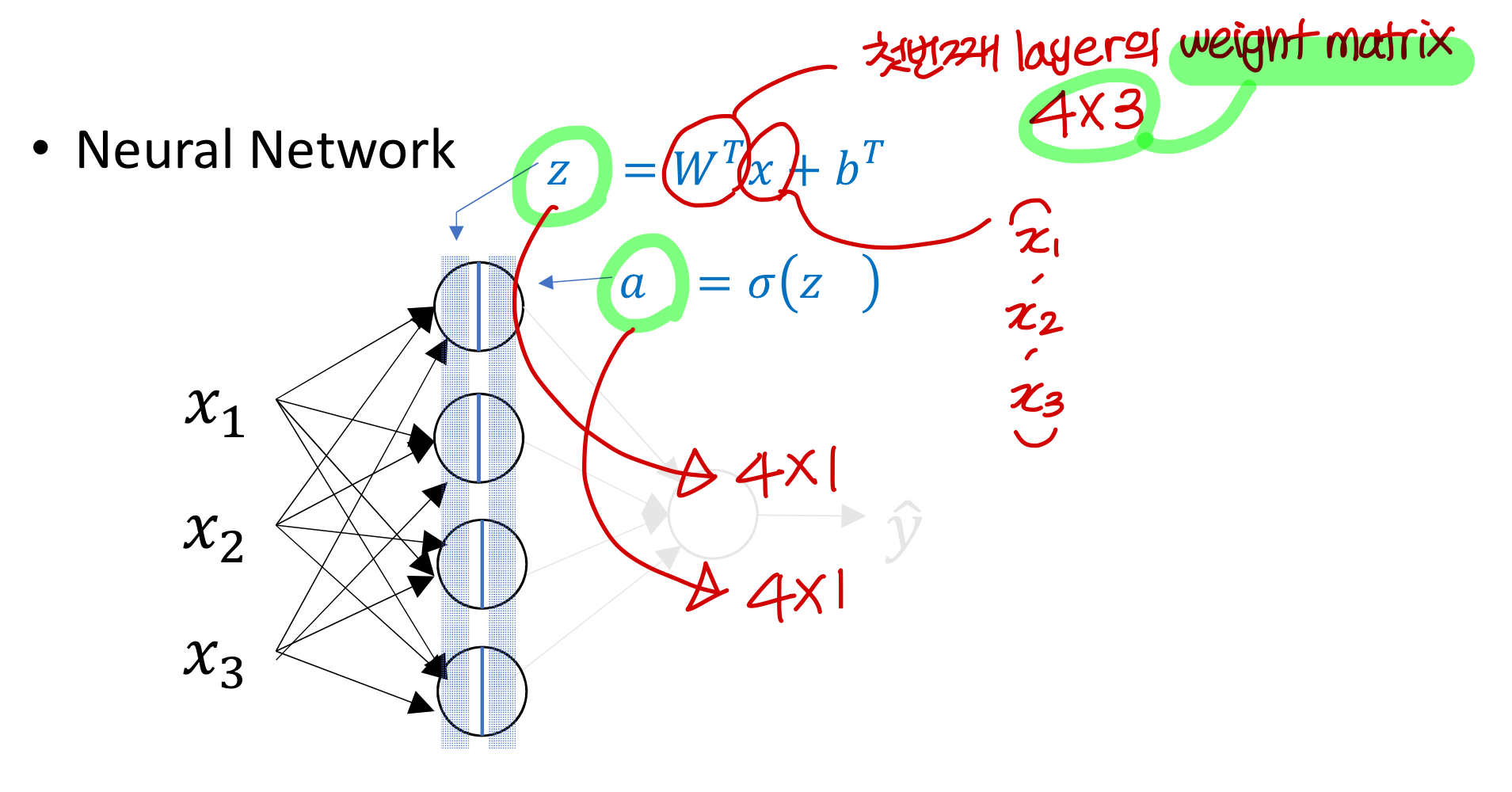
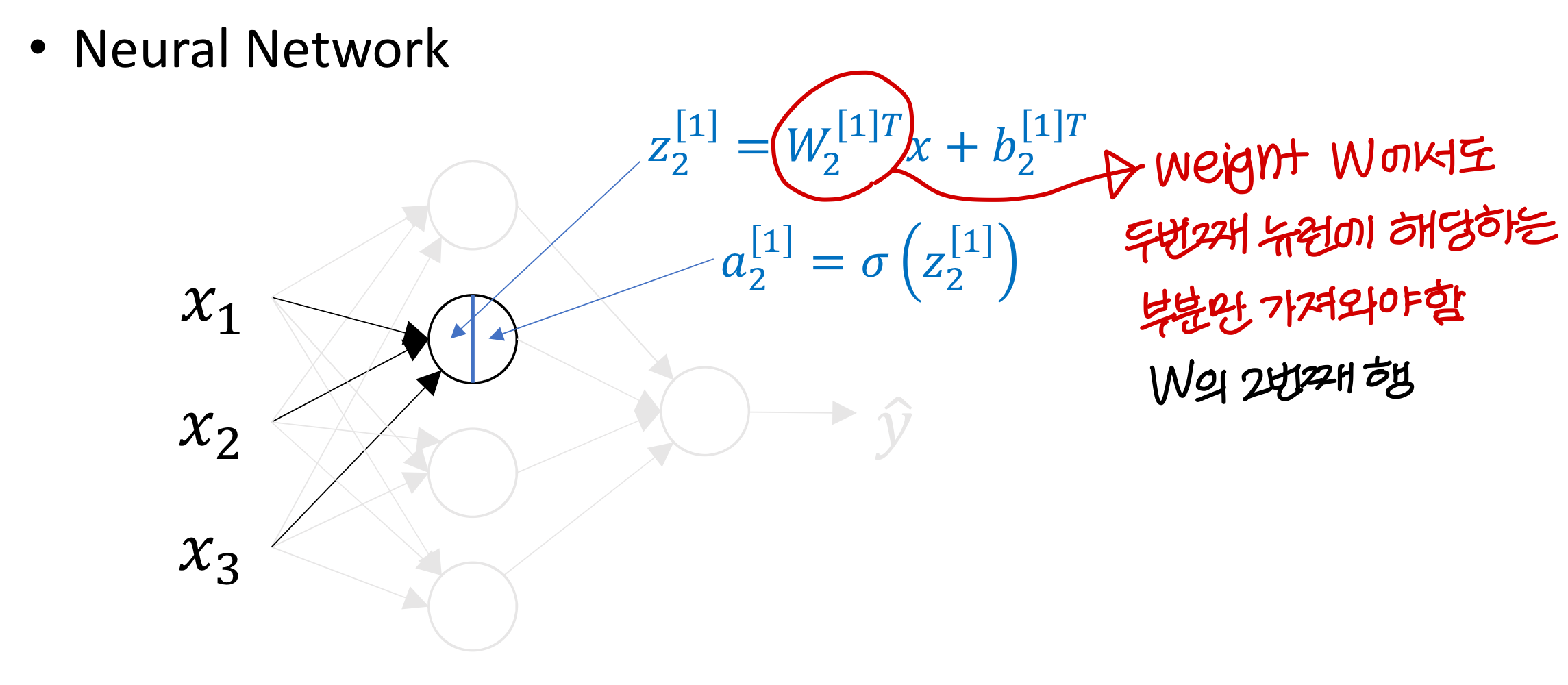
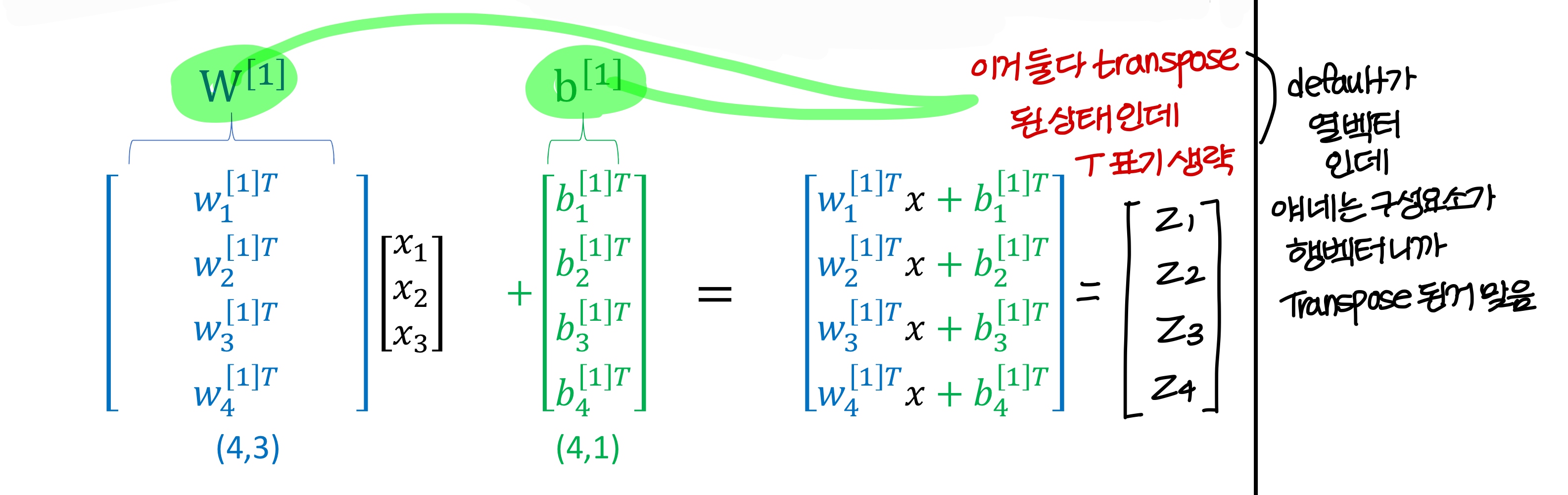
• 근데 weight matrix, bias 특이하게 transpose 해서 사용함

  

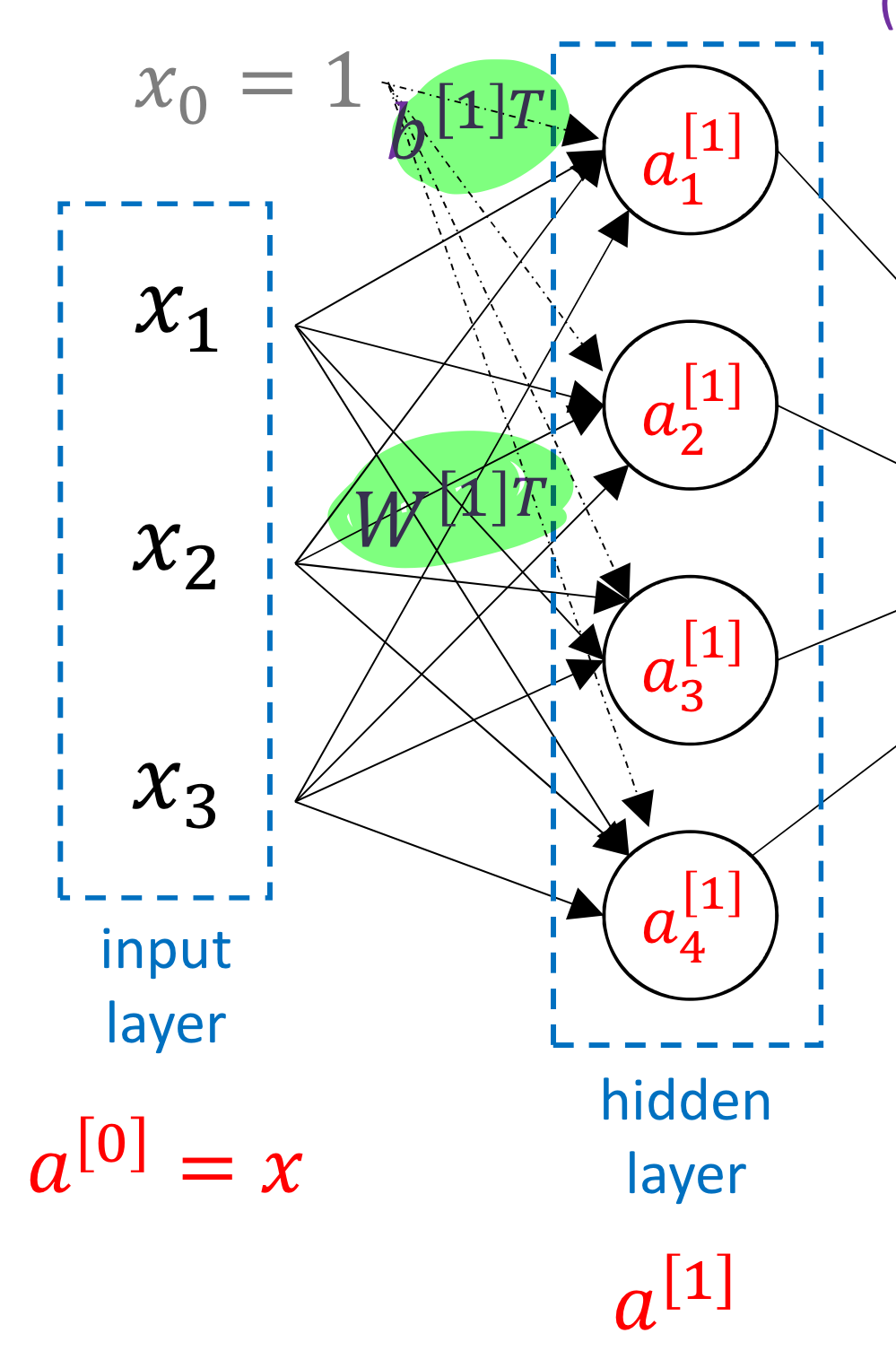
  : 이런식으로! → 왜 이렇게 사용할까?

  → 고등학교때까지는 행벡터(가로로) 많이 썼지만 이제는 열벡터(세로로) 많이 쓴다.

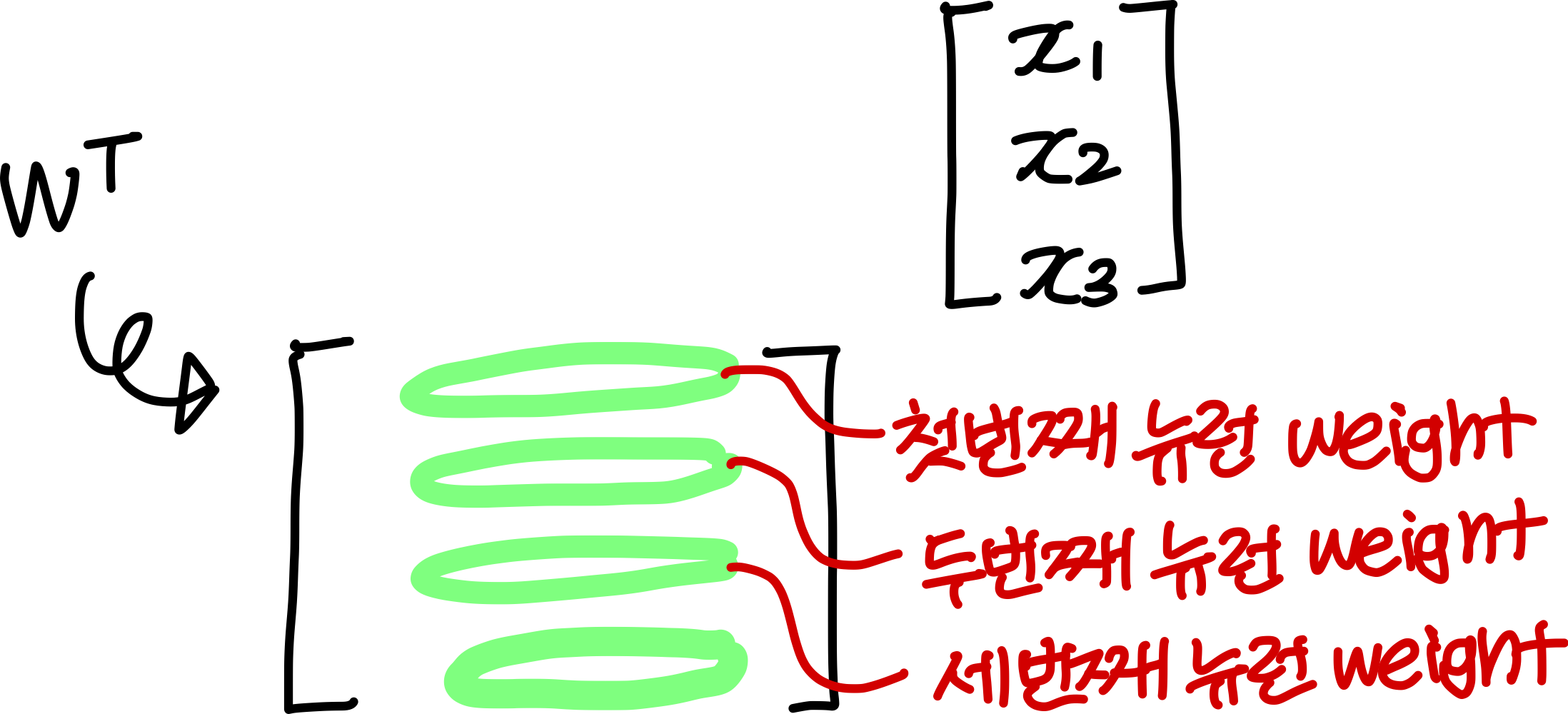
  → weight matrix가 3X4면 (3x4: weight matrix) (3X1: input)이 계산이 안된다.

  그래서 관습적으로 weight matrix는 transpose를 해서 나타내게 된다.

---

• linear combination의 결과를 $z$, activation function의 결과를 $a$라고 표기

  

Computing NN’s Output

→ 이렇게 여러개의 뉴런으로 구성된 neural net이 있음

---

→ 이렇게 input을 열벡터로 나타내어 깔끔하게 처리함

→ 이때 weight 만들때 $W^T$에서

첫번째 행은 첫번째 뉴런의 weight

두번째 행은 두번째 뉴런의 weight

세번째 행은 세번째 뉴런의 weight..

---

→ 표기 주목

→ 위에 표기하는 [I]는 layer

→ 아래쪽에 표시하는 i는 layer의 몇번째 뉴런인지

→ weight에서도 layer의 i번째 뉴런에 해당하는 부분을

$W_i$ 이래 표현함

---

최종적인 계산은 이렇게

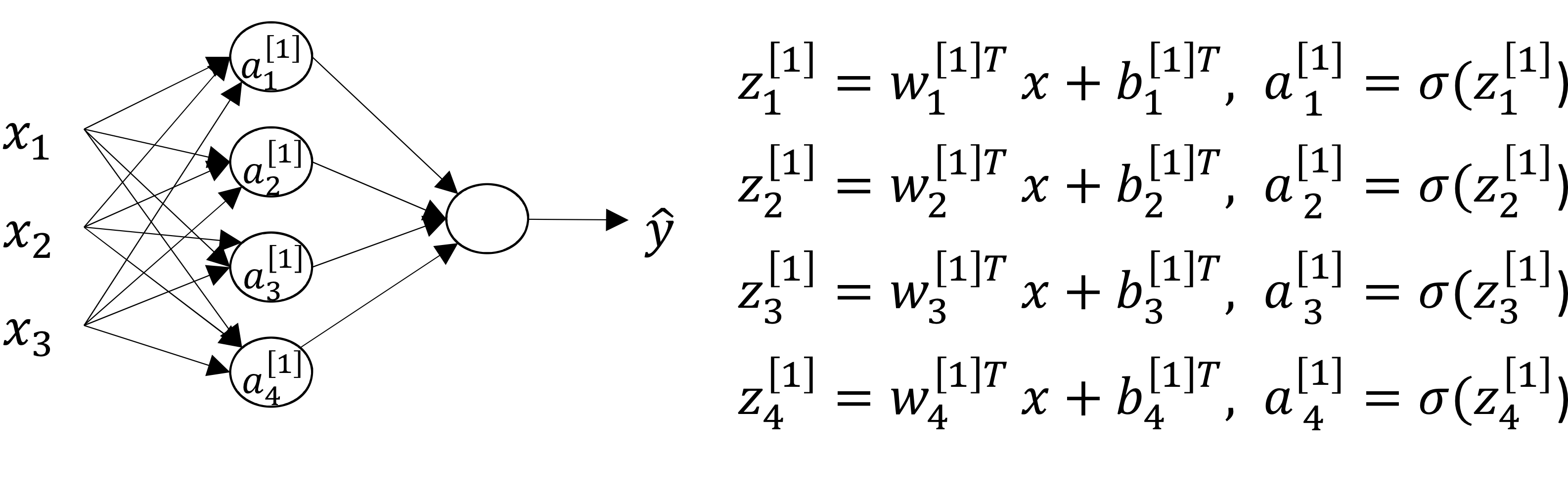
→ 뉴런의 출력값을 하나하나 계산하는 For-loop를 계속 돌리는건 상당히 비효율적임

→ 그래서 matrix 연산을 사용해 계산을 효율적으로 할거임

• linear regression 통과한 상태

• activation function까지 통과하면

  

💡

앞으로도 W와 b에서 transpose 표기 생략할거임. default로 transpose 되어 있다고 보면 된다.

→ matrix와 vector 크기 확인하기

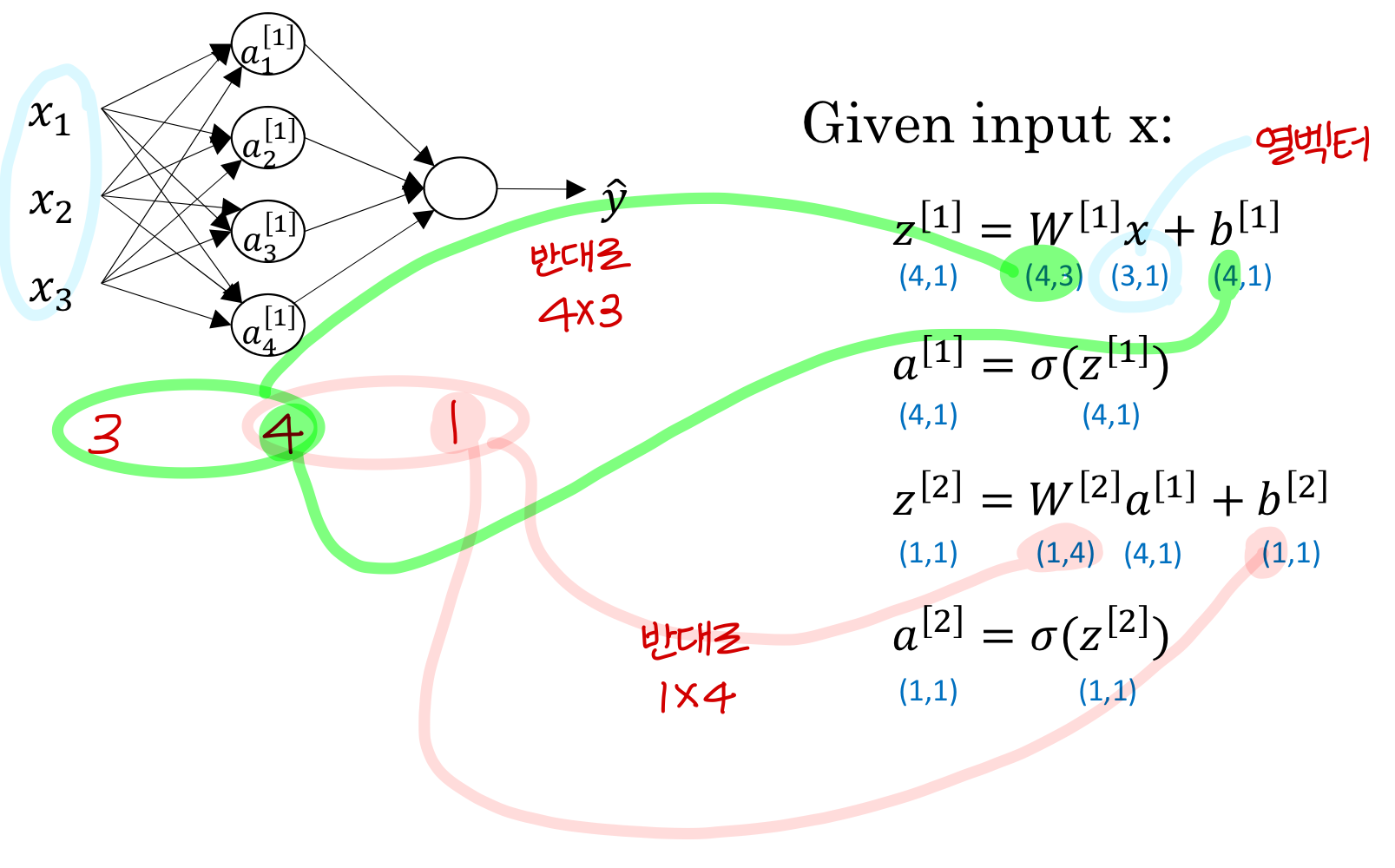
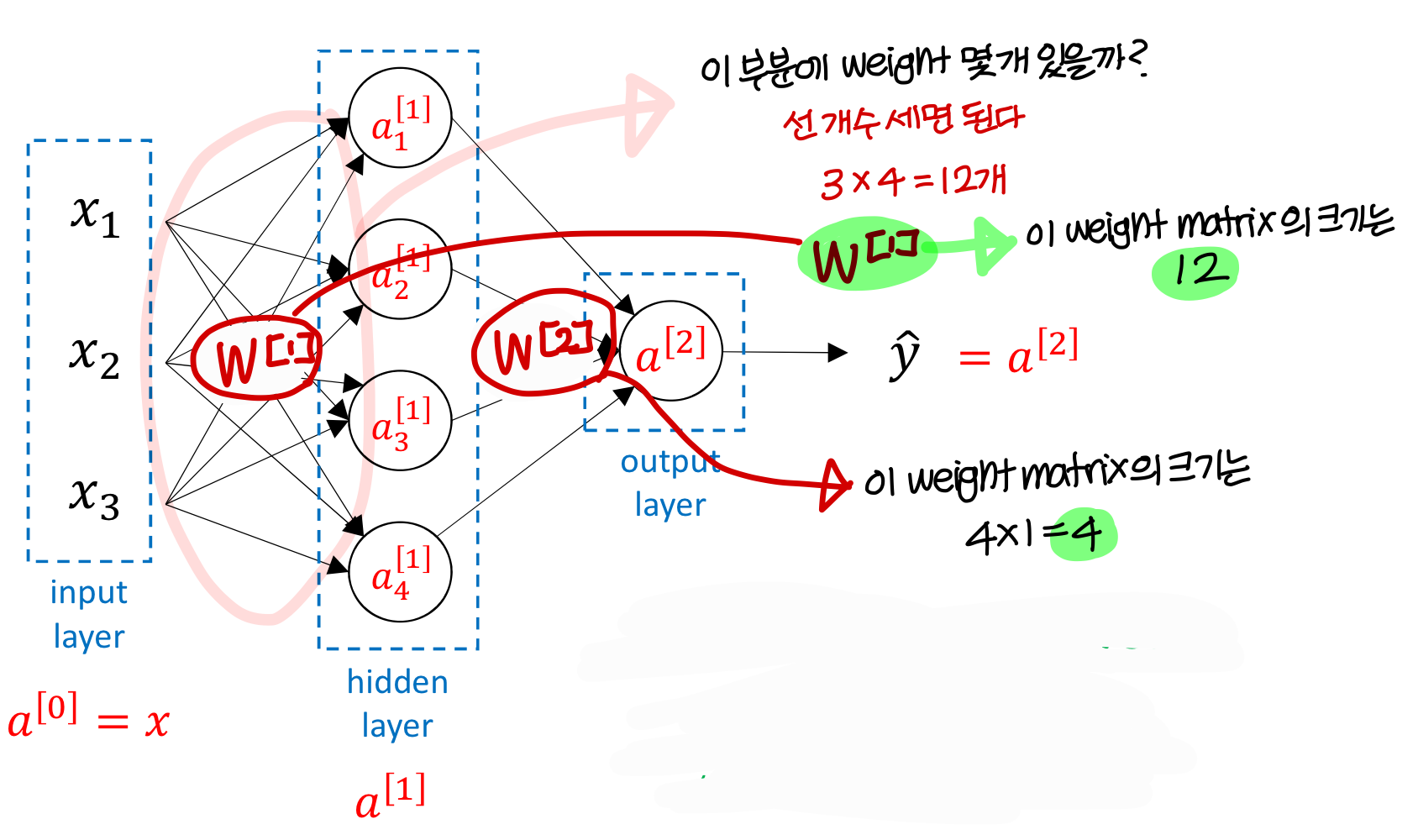
• weight matrix는 (뒤에 layer, 앞에 layer)

• bias는 (뒤에 layer, 1)

• linear combination 통과한 z값도 (뒤에 layer, 1)

• activation function 통과한 a값도 (뒤에 layer, 1)

💡

z와 a가 열벡터(column vector)라는 사실 꼭 기억하자

---

Vectorizing across multiple examples

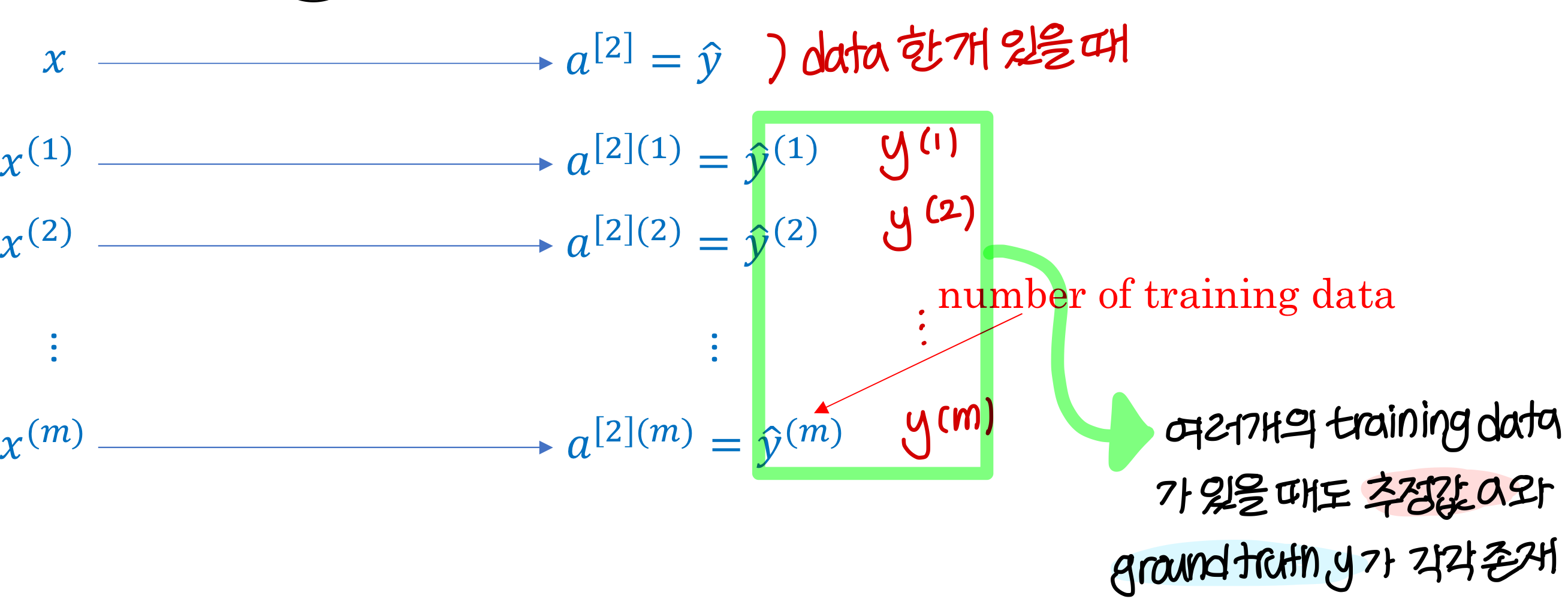
→ 지금까지는 하나의 training data에 대해서 하나의 z가 정해지고 하나의 a가 정해지는걸 봤음

→ 하지만 실제로는 training data 엄청 많음!!

→ 여러개의 training data가 있을 때 추정값 a도 여러개, ground truth도 여러개

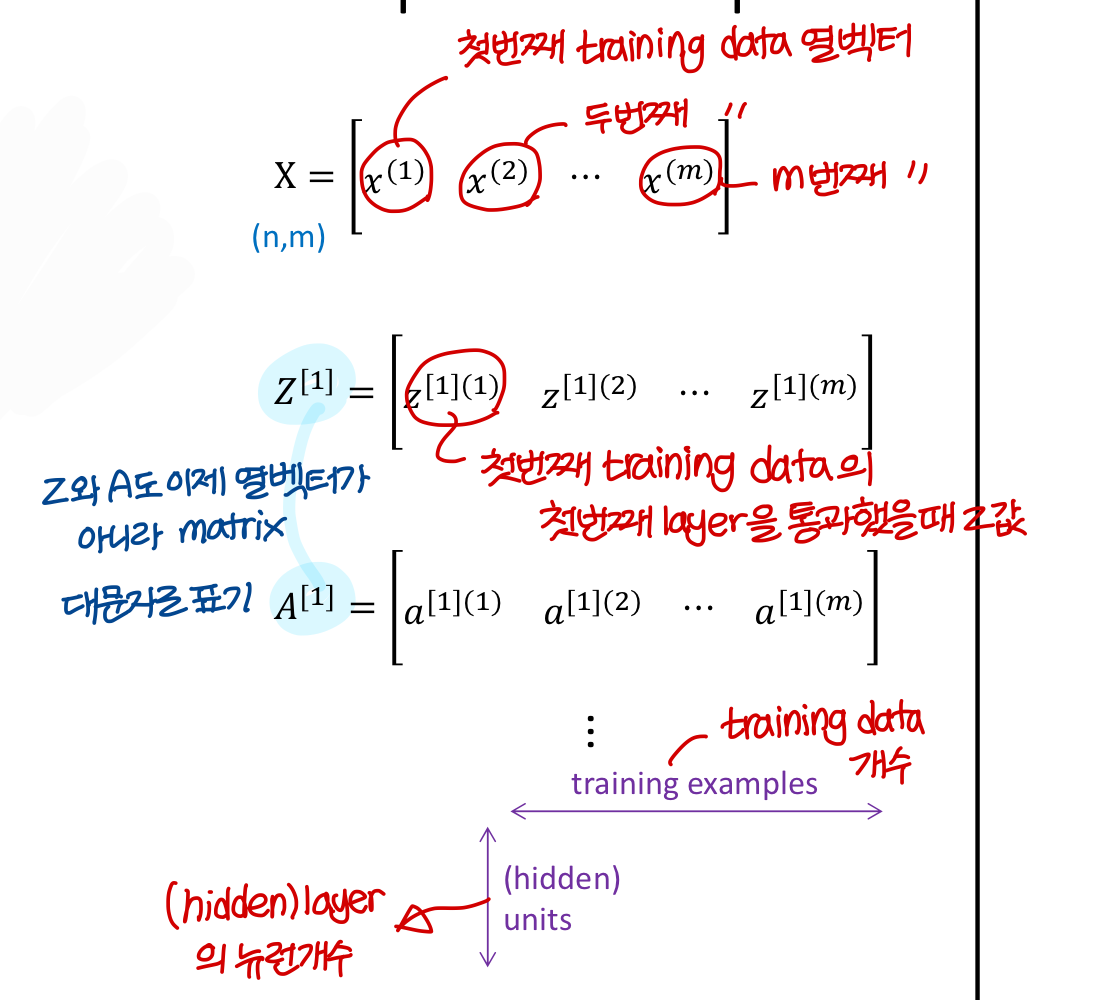
→ training data가 많아지면 이제 x 자체도 하나의 column vector가 아니라 matrix로 표현가능

어차피 training data 다 돈다음에 weight, bias update 하기 때문에

한 iteration에서 곱하는 weight matrix, bias 동일함

그러니까 모든 training data 한번에 곱해버리자!

---

각각의 training data에 대해 하나하나씩 연산

x를 column vector로 놓고, 한번에 곱하지 않는 예시

(non-vectorized implementation)

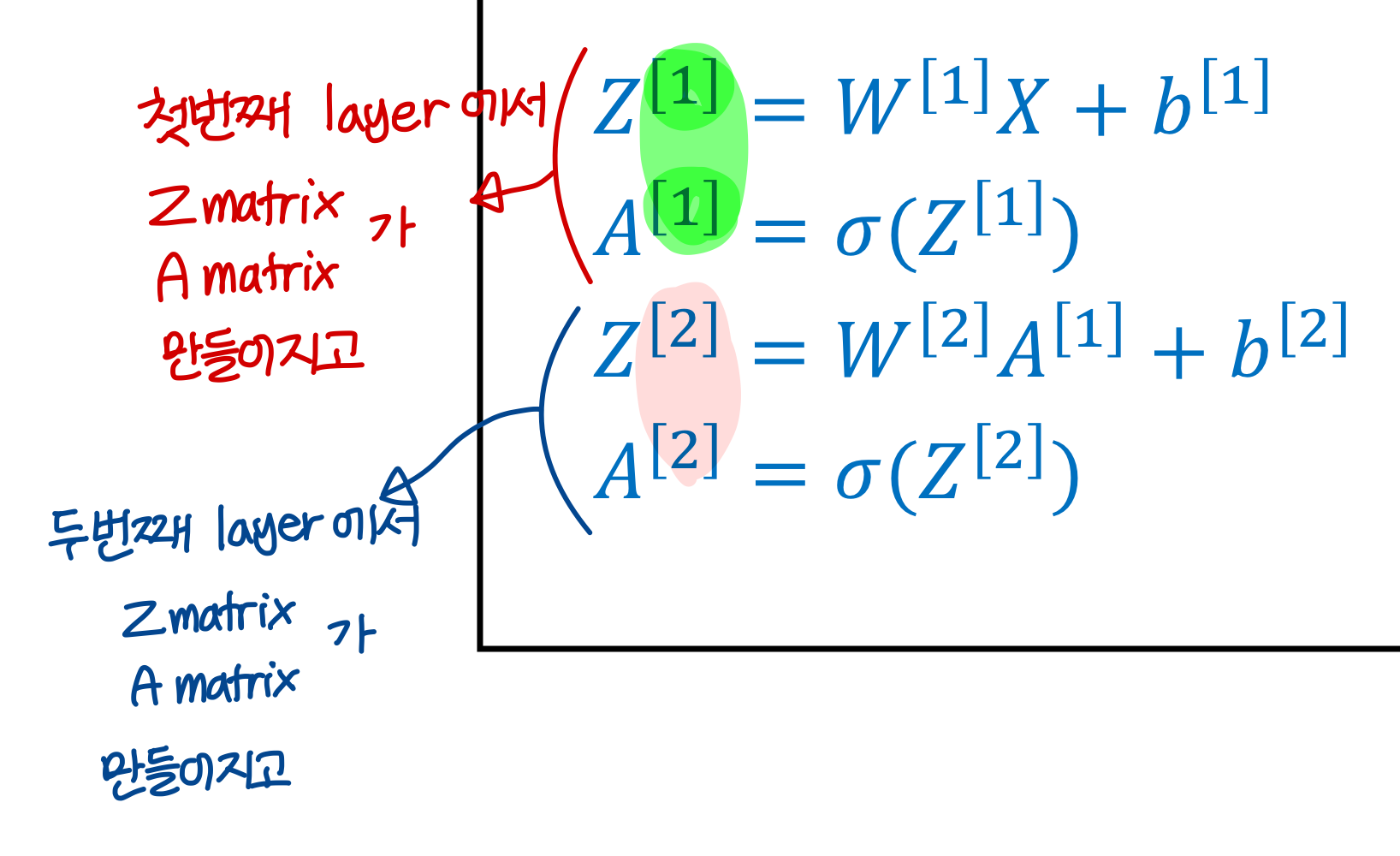
모든 training data에 대해 한번에 연산

💡

모든 training data에 대한걸 의미할 때 x, z, a를 모두 대문자로 표기함

• X, Z, A는 이제 열벡터가 아니라 matrix

• 행 개수는 해당 layer의 뉴런 개수

• 열 개수는 training data의 개수

---

→ 이렇게 각각의 layer에 대해해 Z matrix와 A matrix가 만들어짐

---

A Quick Example: 2 Layered (shallow) Neural Network by Gradient Descent

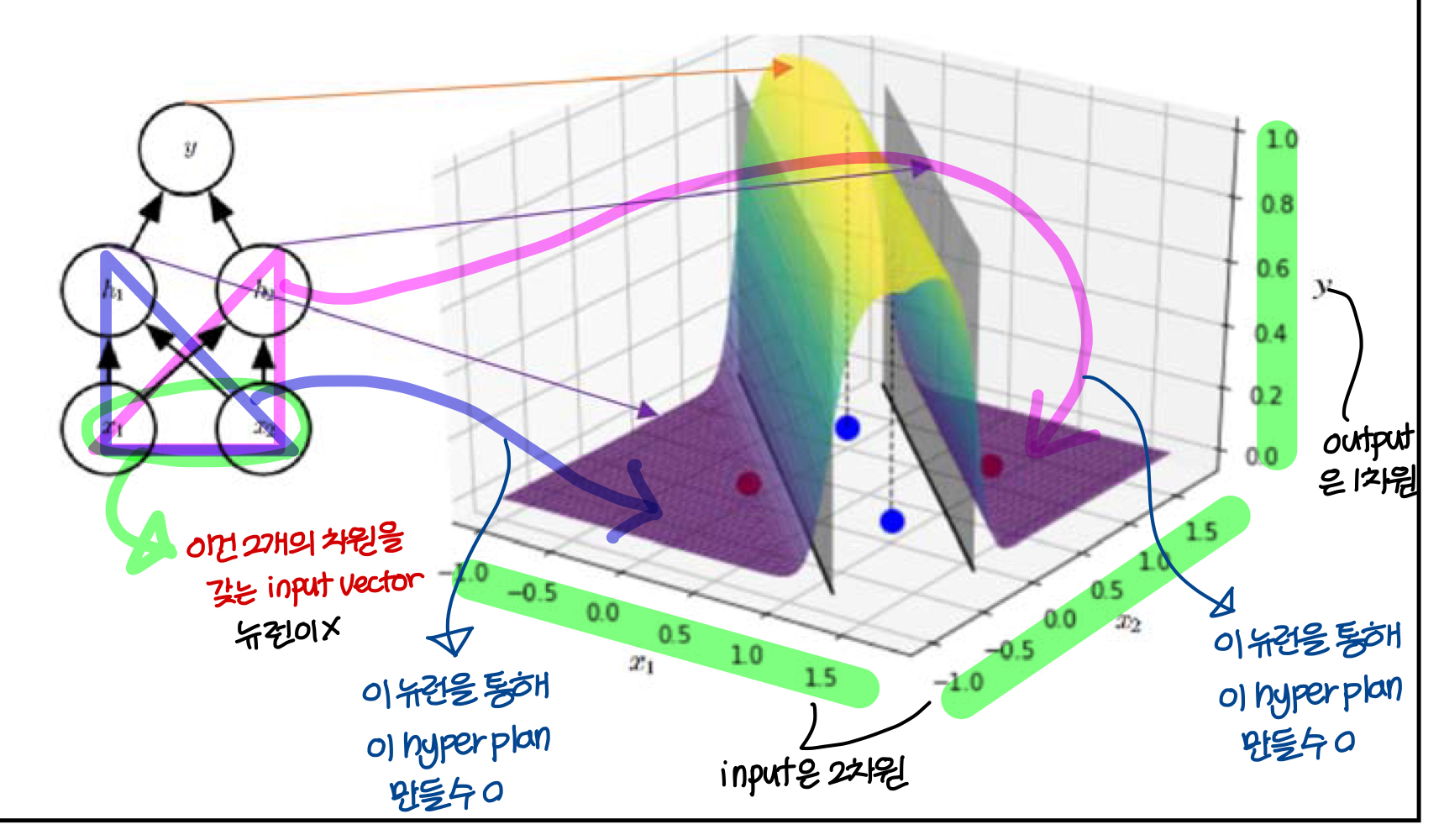
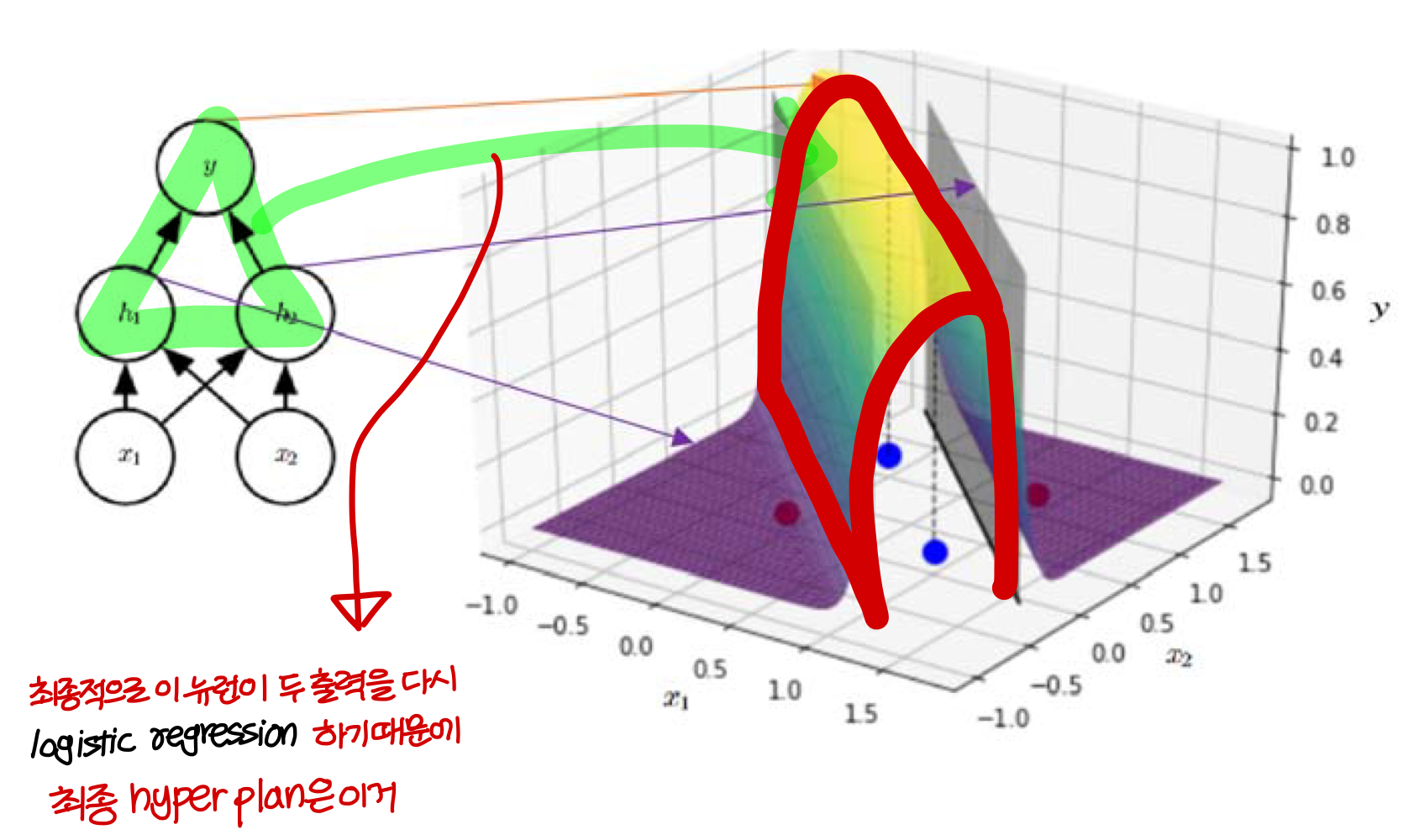
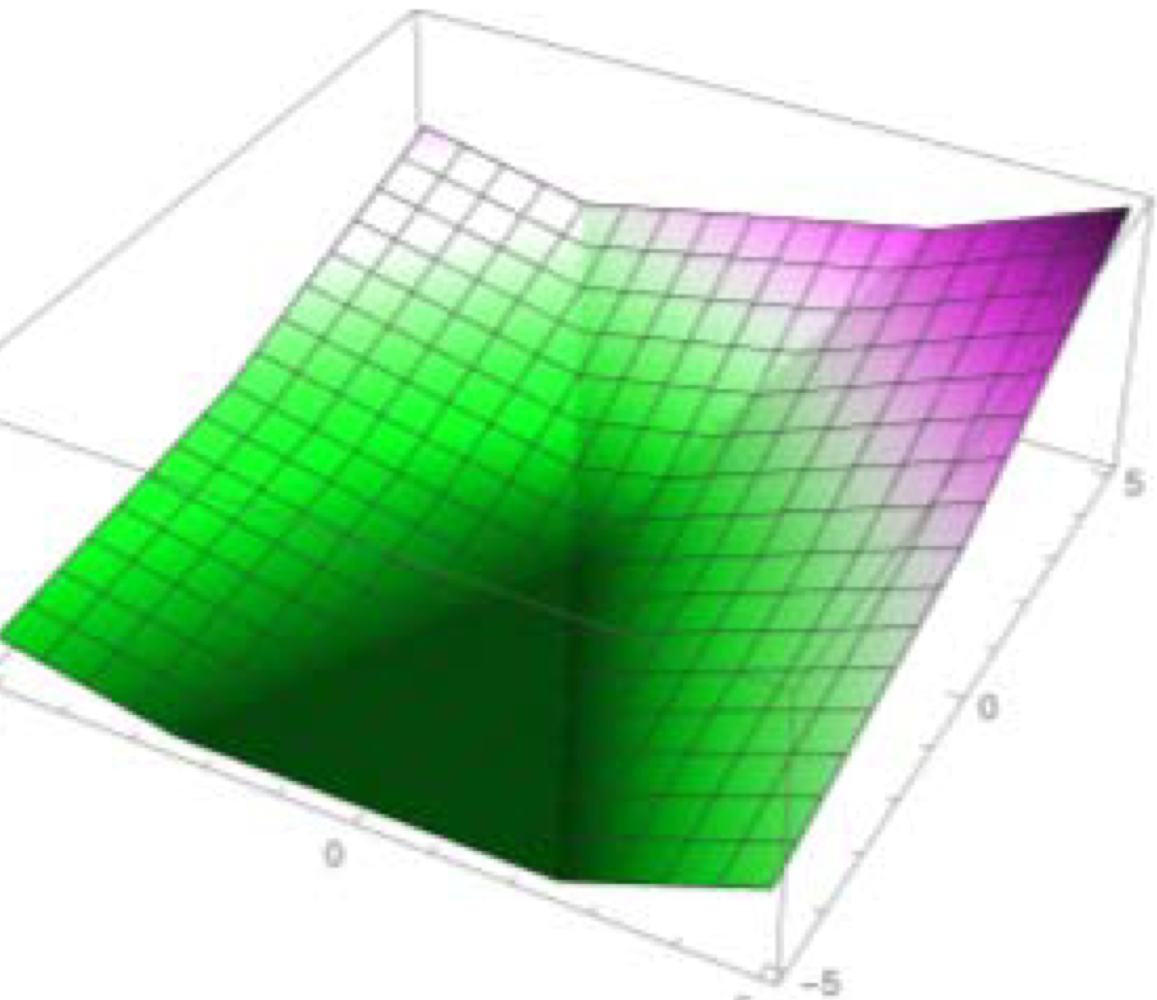
→ 결론적으로 빨간점에 대해서는 0에 가까운 값이 나오고, 파란점에 대해서는 1에 가까운 값이 나오도록 하는 hyper plan을 만들 수 있음

→ 이런 hyper plan은 뉴런 하나로는 만들 수 없음

---

Another Example: Deep (Layered) Neural Network by Gradient Descent

• 이렇게 layer를 많이 두고

• layer마다 뉴런의 개수도 충분히 넣으면

→ 아래 그림처럼 복잡한 형태의 hyper plan 만들 수 있음

---

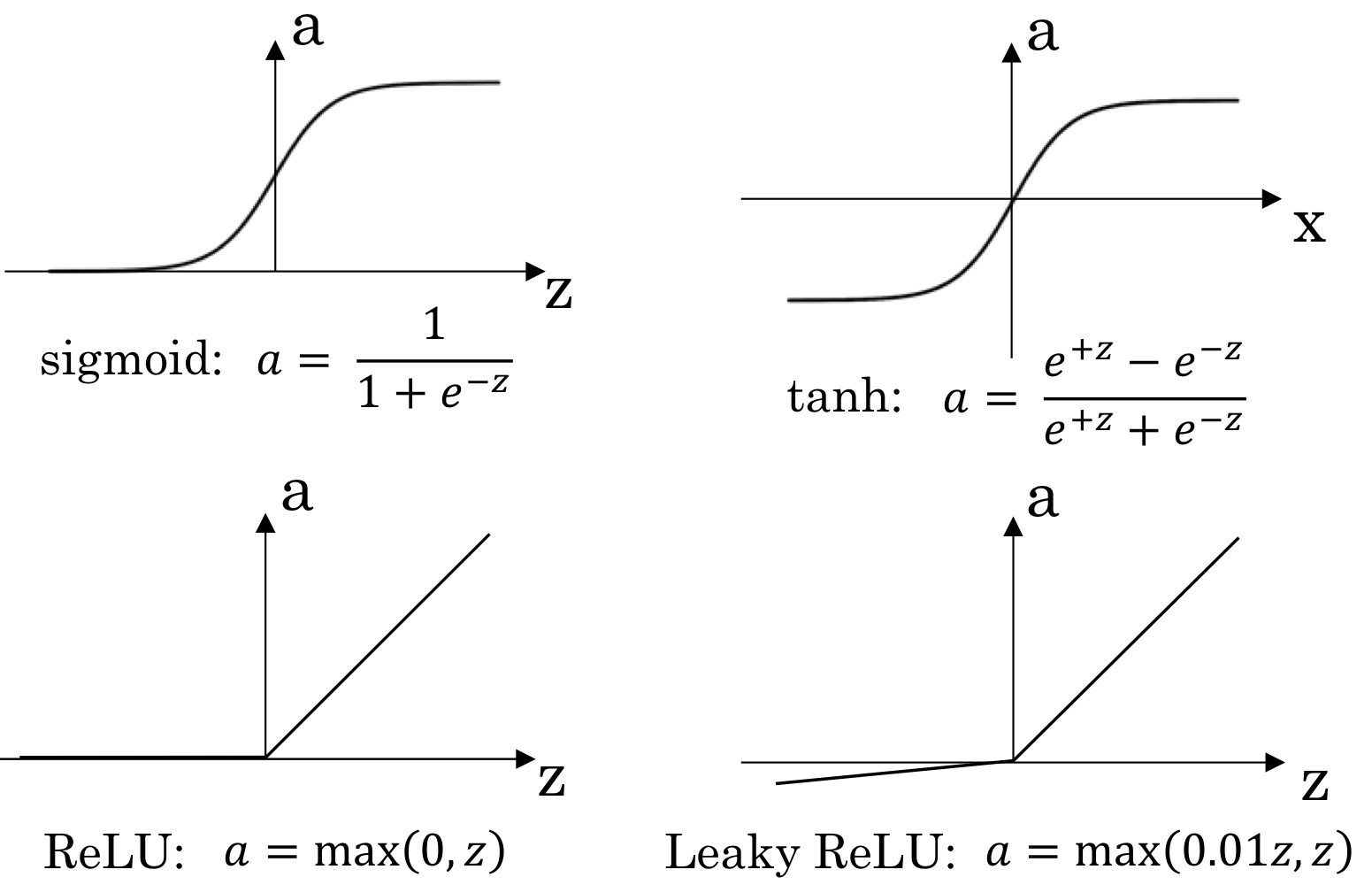
Activation functions

• 지금까지 activation function으로 sigmoid function만 이야기 했는데 그것만 있는게 아님! 종류 많음!

💡

일반적으로로 activation function으로 non-linear function을 사용함

• 경우에 따라 용도가 다름

  어떤 activation function을 사용할지는 neural net을 구성할 때의 option임

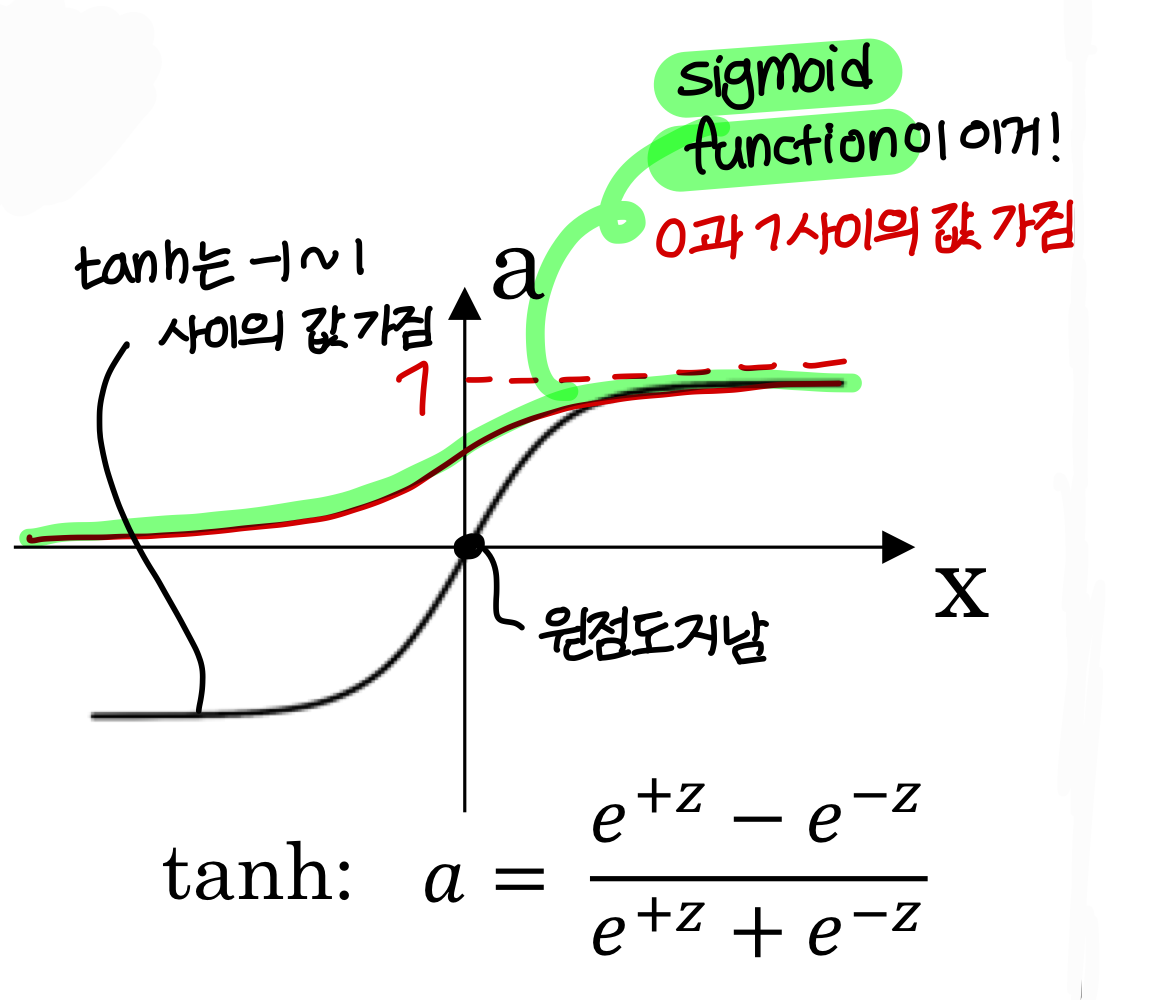
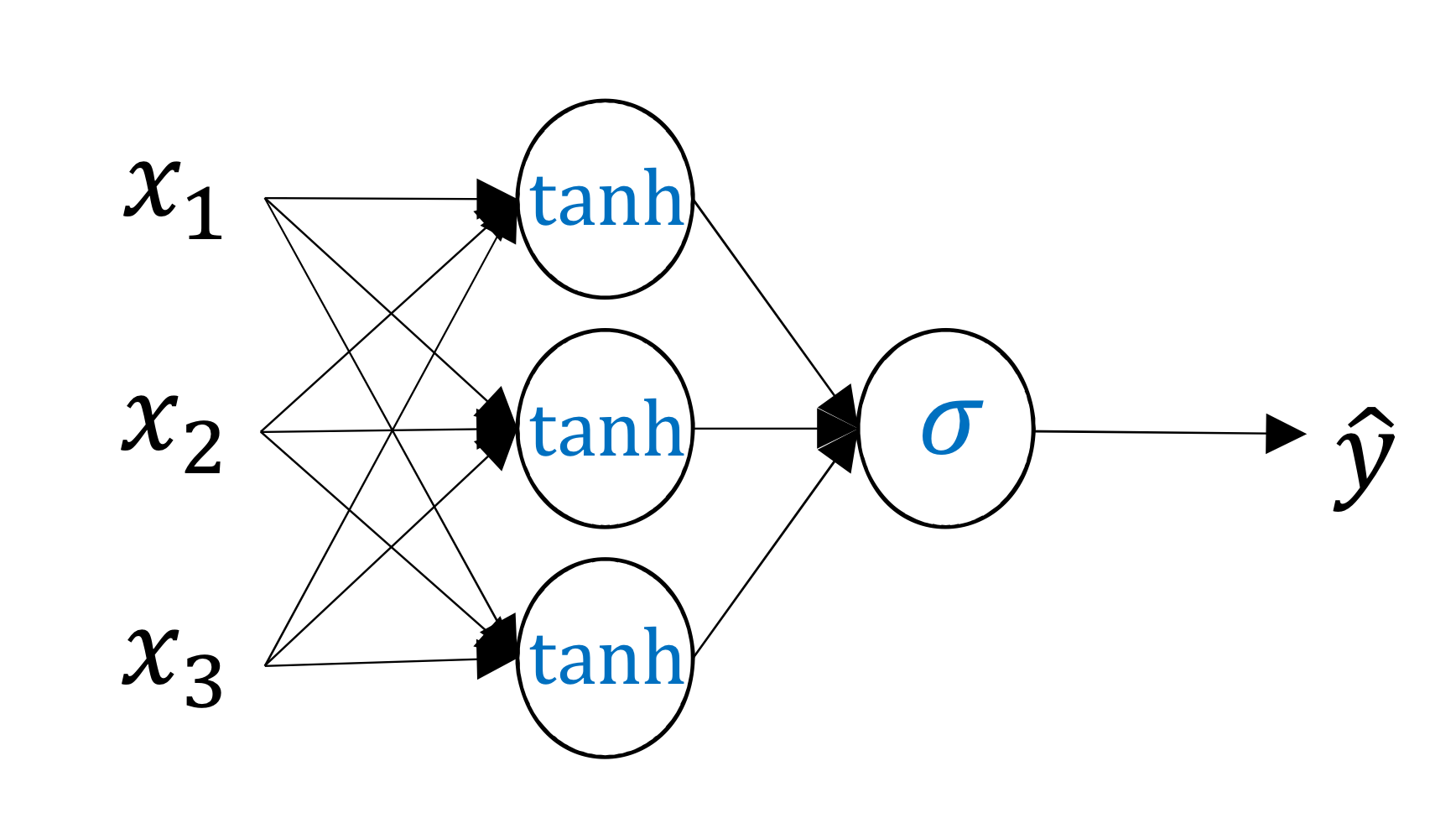
tanh (hyperbolic tangent)

• 이렇게 생김

  

→ 일반적으로 sigmoid function을 쓸 때보다 학습이 더 잘되거나, 학습된 neural net의 성능이 더 좋을 수 있음(항상 그렇다는게 X)

→ z 값이 충분히 크거나 충분히 작으면 기울기가 0에 가까워진다.

그러다보니 gradient를 곱해나갈 때, gradient가 vanishing 되는 문제 발생

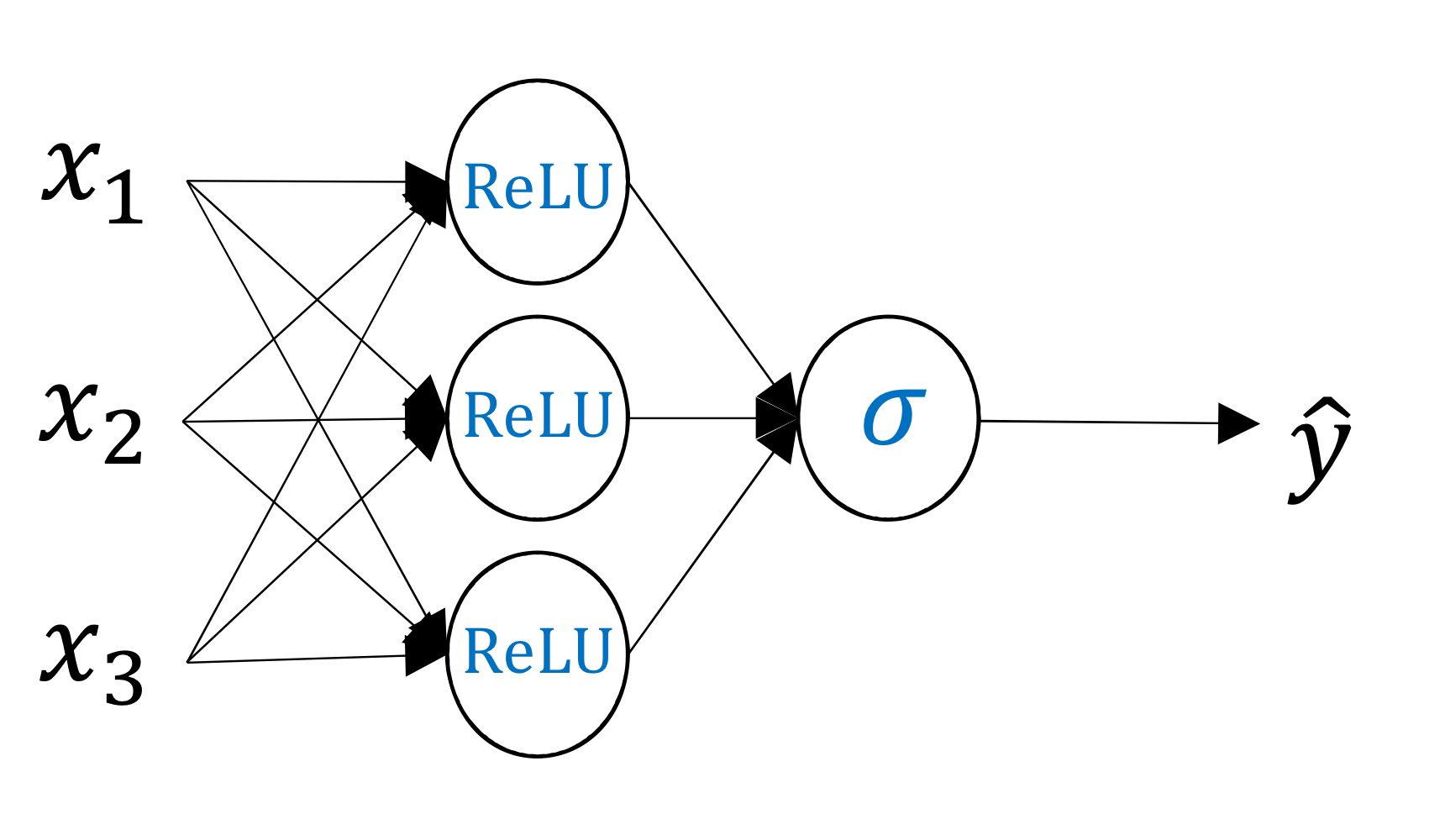
→ 그래서 hidden layer의 activation function으로로 ReLU 함수를 사용하는게 점점 핫해지고 있음

---

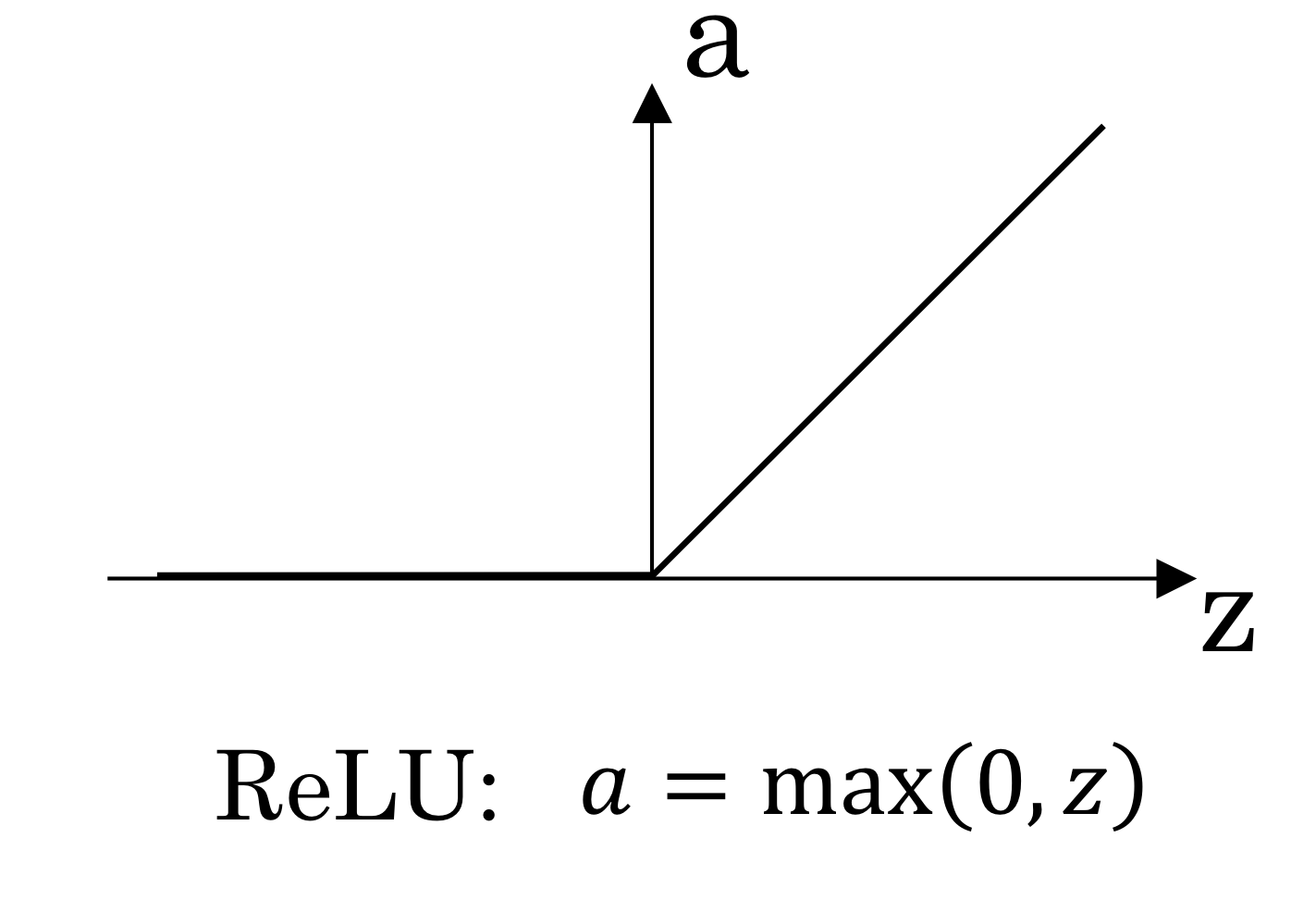
ReLU(렐로 함수)

• 이렇게 생김

  

  → 이렇게 단순한 형태를 activation function으로 사용하는 경우도 많음

• 양수인 경우에는 미분값이 1이고, 음수인 경우에는 미분값이 0임

  → 미분값이 1 아니면 0이기 때문에 계속 작아지는 문제가 발생하지 않음

  → 계산도 훨씬 쉬움

Leakey ReLU

• ReLU랑 비슷한데 양수일때는 그대로 반영하고 음수일때는 약하게 반영

• 이렇게 생김

  

• 음수쪽 기울기 0.01 정도

---

💡

(binary classification 문제에서, output을 ~인 확률로 사용하는 경우) → output 쪽 activation function으로 sigmoid function 쓰는게 일반적

: ReLu function 같은 경우 값이 끊임없이 커지기 때문에 이걸 확률로 사용할 수 없음) 0~1 사이의 값이 나오는게 아니니까

💡

hidden layer의 activation function으로는 ReLU 쓰는게 일반적

Recap: Activation functions

Why does neural network need non-linear activation function?

• 근데 neural net에서 linear regression처럼 linear activation function을 안쓰고 왜 non-linear activation function 쓰지?

---

• activation function을 사용하지 않는다면, (또는 activation function으로 identity function을 사용한다면)

  

• model의 hyper plan 그렸을 때 이런식으로 나옴

  

  → 이렇게 엣지가 생겨서서 경계값에서 출력값이 급격하게 변하는 형태로 만드어짐

---

• hidden layer에서는 linear activation function 쓰고, 마지막에 sigmoid를 쓴다면?

  

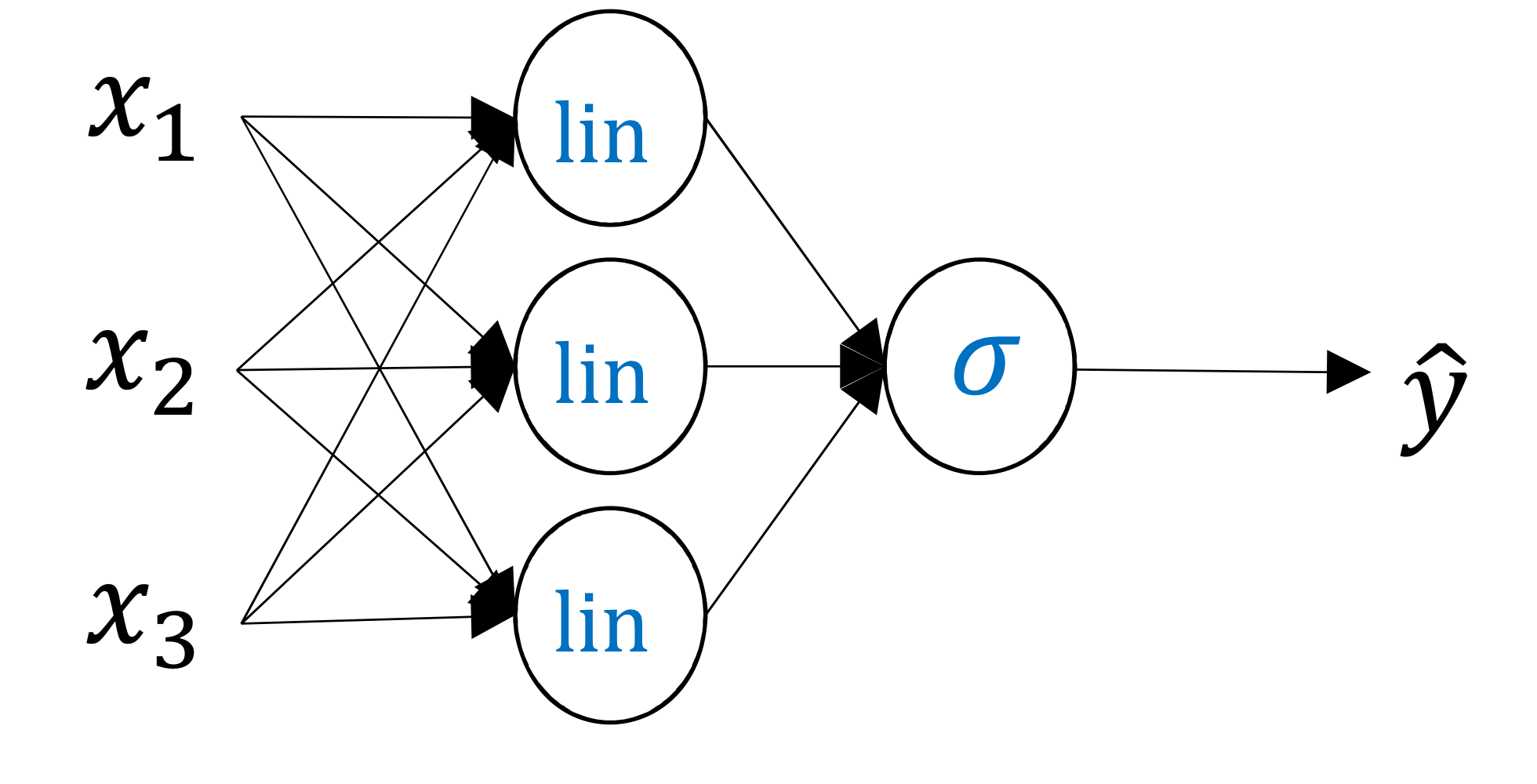
  → 근데 이렇게 하면 뉴런 하나짜리 standard logistic regression이랑 표현력이 그다지 다르지 않음

Derivatives of Activation function

💡

이제 activation function 미분해볼거임

Sigmoid activation function 미분

Tanh activation function 미분

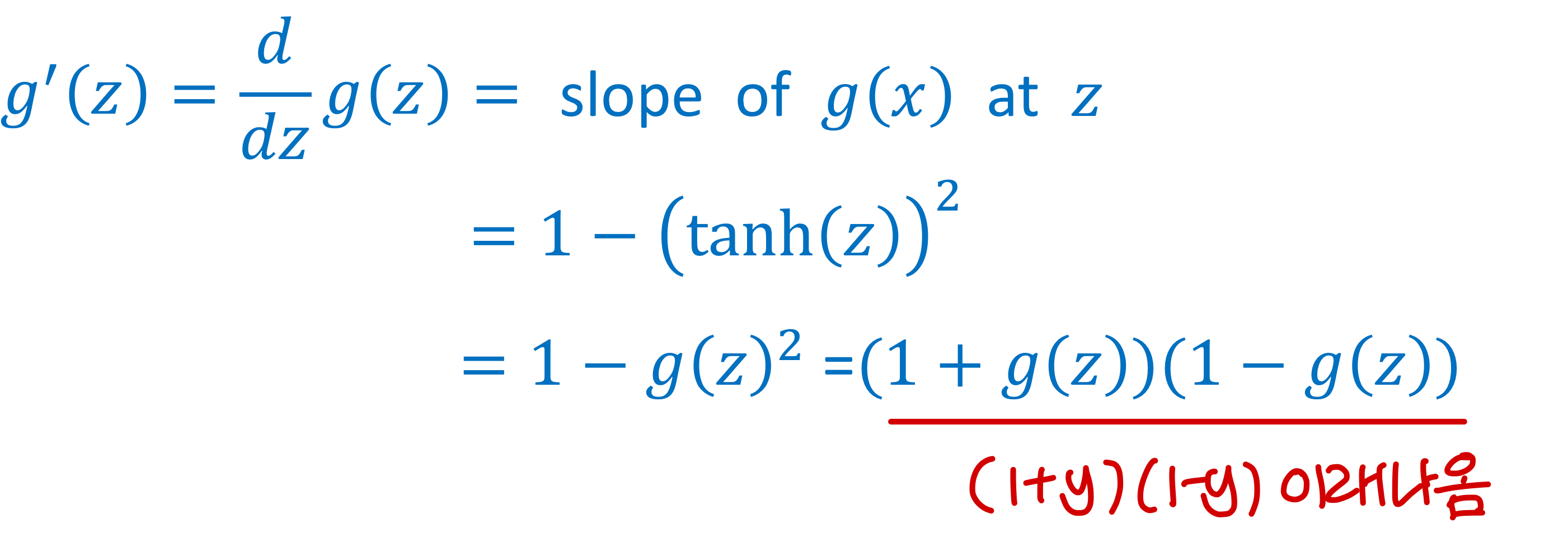
ReLU and Leaky ReLU 미분

💡

이렇듯 activation function으로로 사용되는 함수들의 미분은 그렇게 복잡하지지 않음

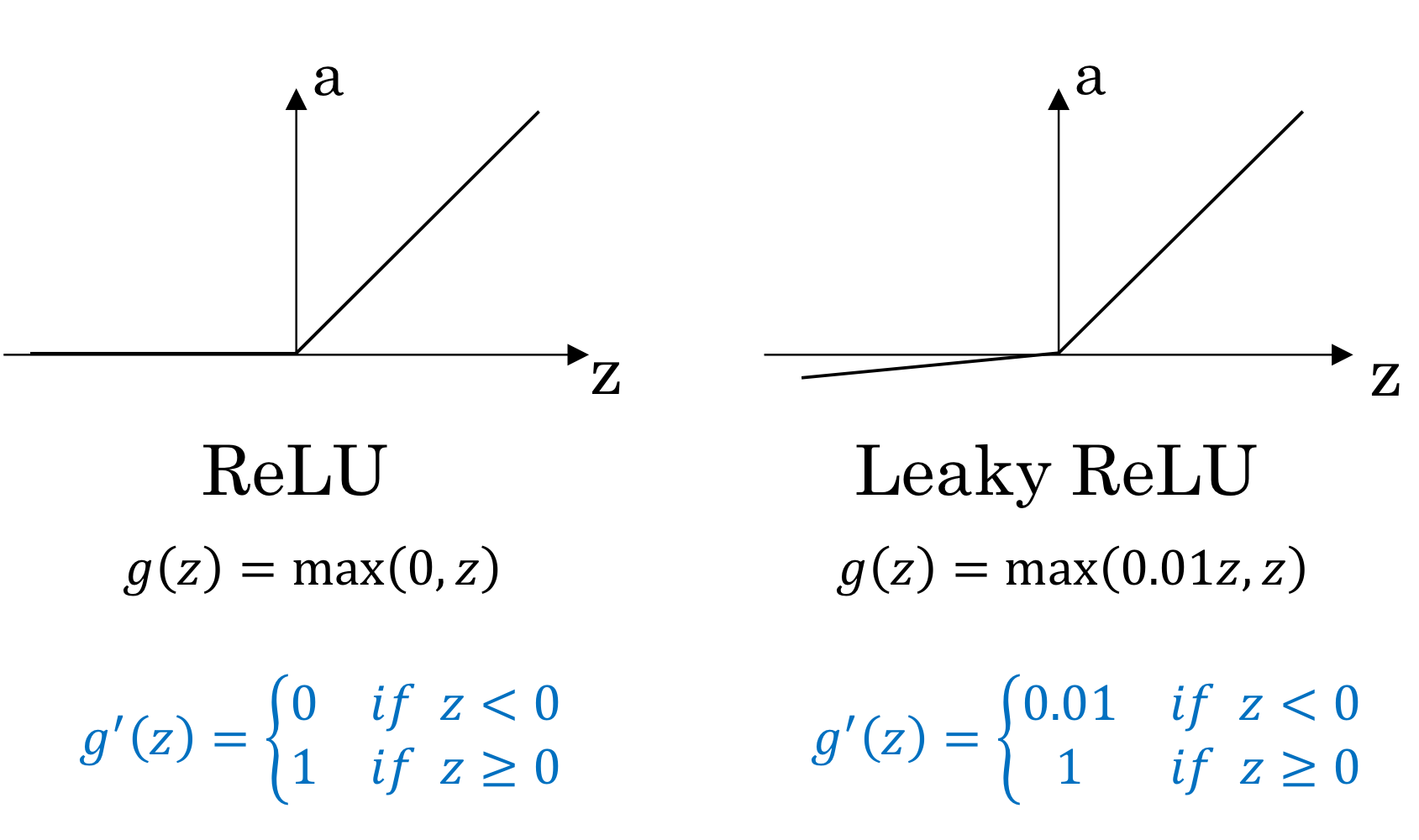
Gradient descent for neural network

• 이제 본격적으로 gradient 구하기 위한 notation 알아보자

• single hidden layer를 가진 neural network

  

  ---

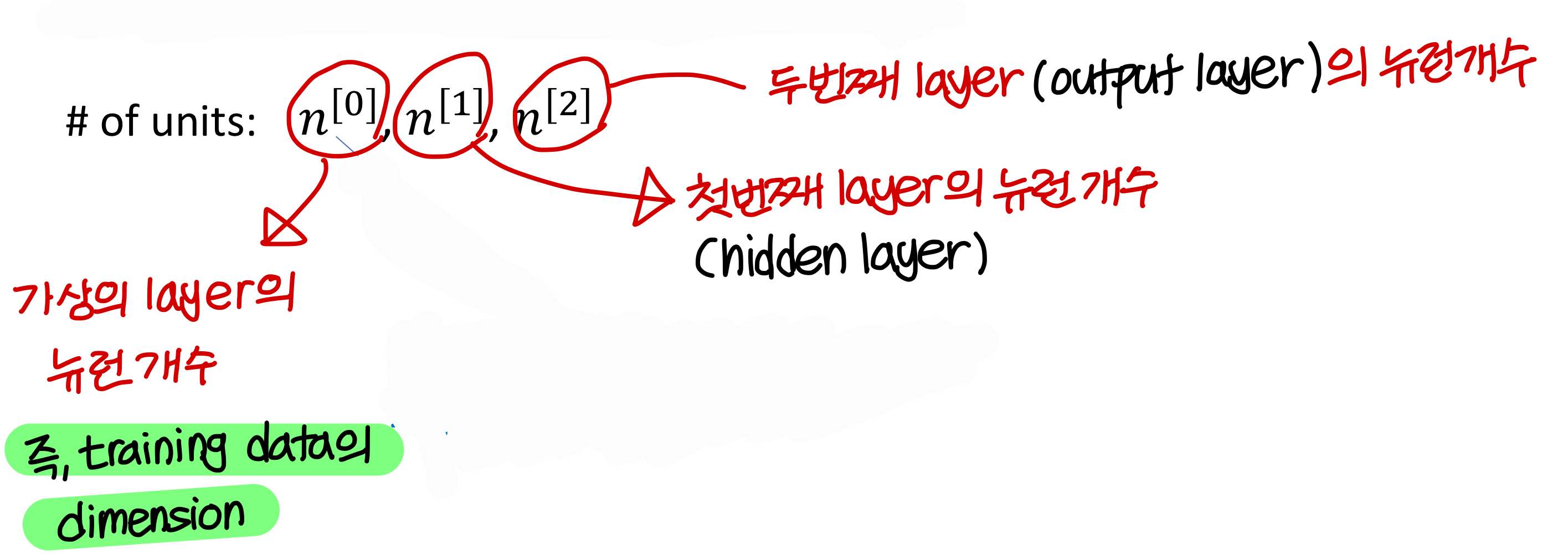
  Parameter는 weight과 bias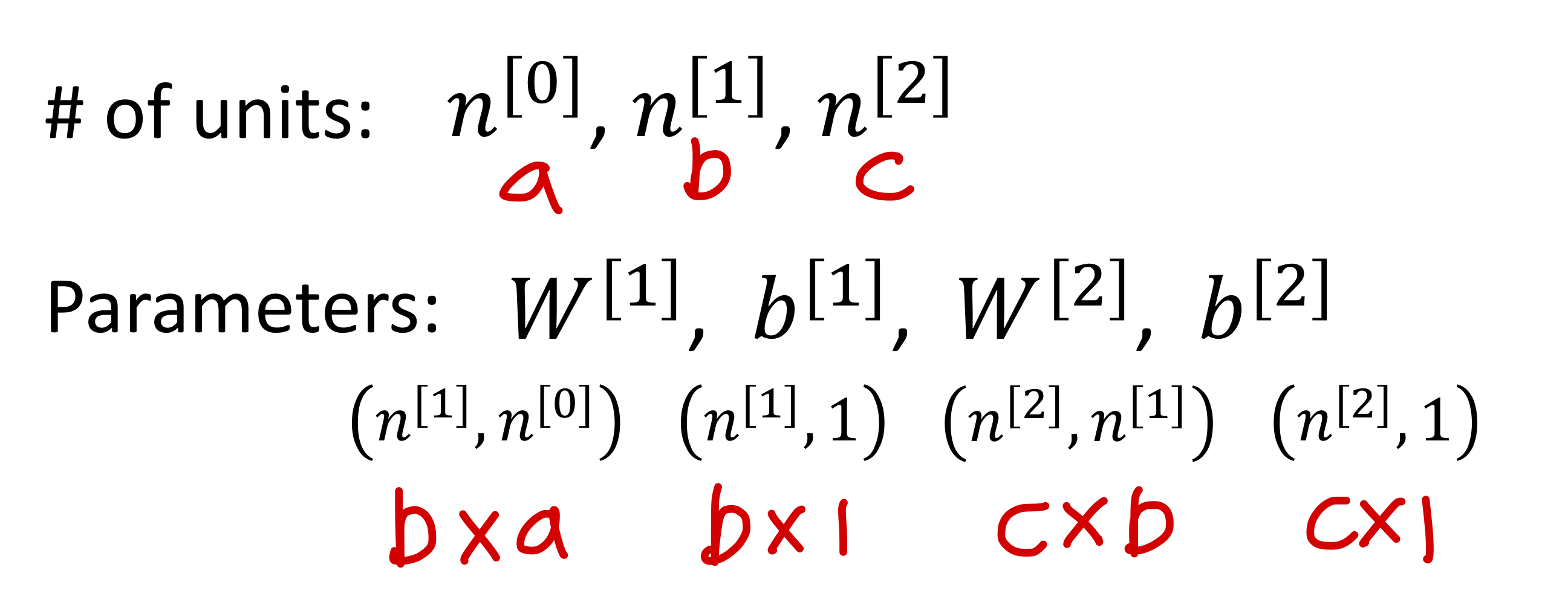

  

  ---

  Cost function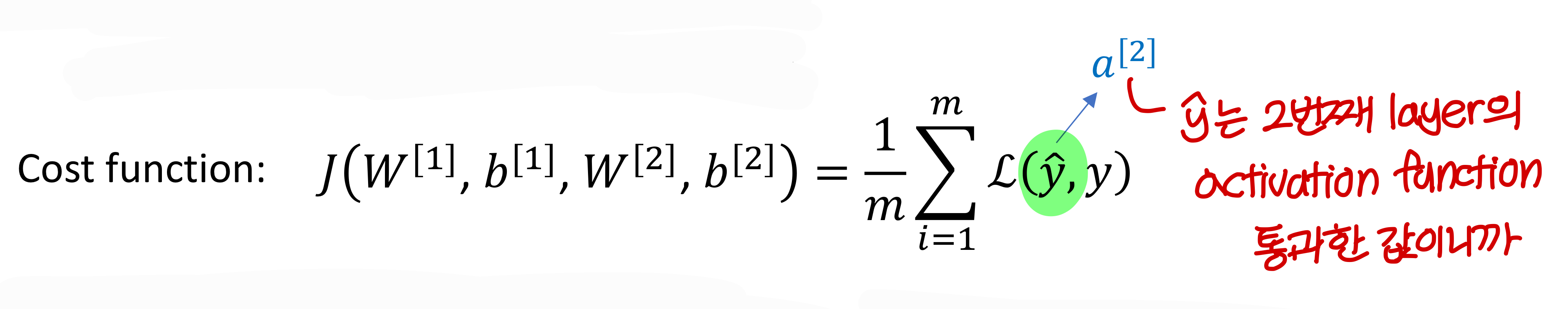

  

  ---

  Gradient descent

  

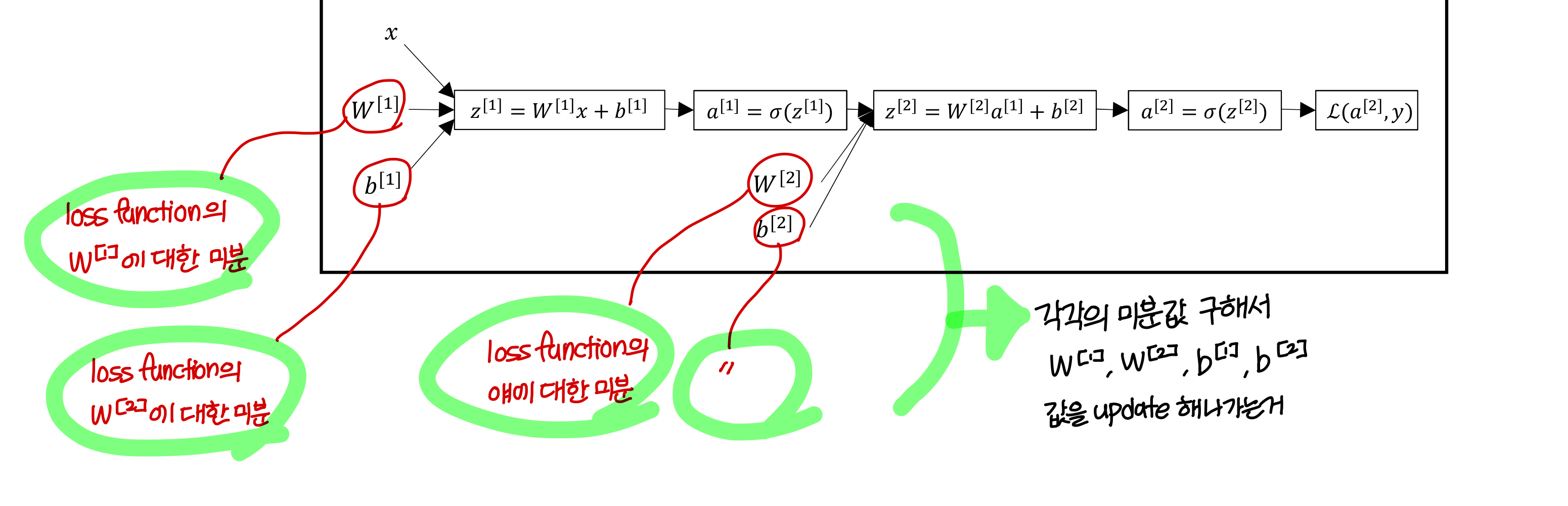
  → 이런식으로 backward propagation을 진행하면서 weight값과 bias 값을 update 해나간다.

Computing gradient

• logistic regression

  

• Two-layer neural network

  (앞에서 본건 layer 1개로 이루어진거고, 이건 layer 2개로 이루어짐)

  

  ---

  

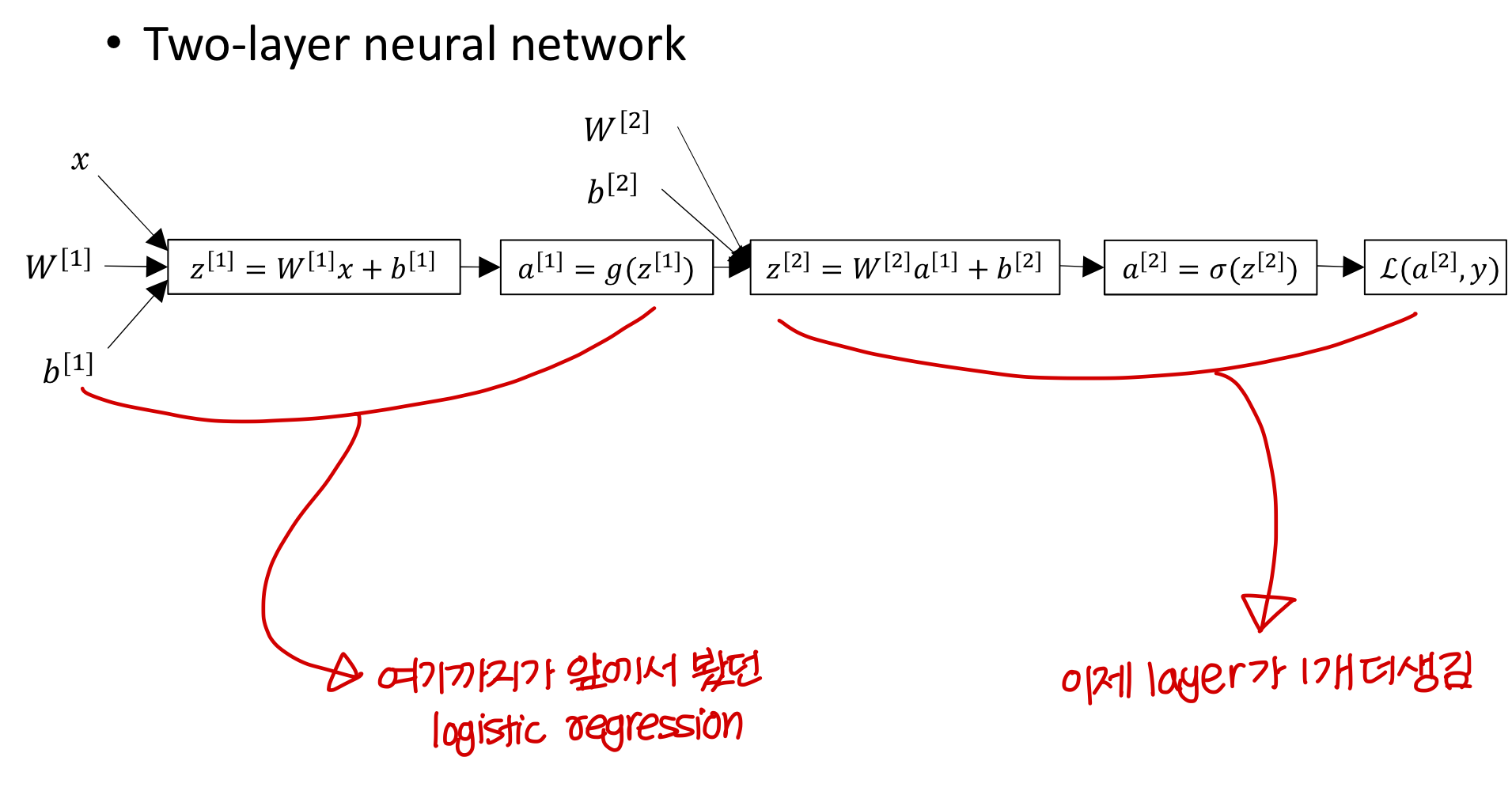
  😑 여러개의 layer로 구성된거 계산할때 주의해야하는게 back propagation에서서 여러 경로 모이는 지점에서 더하기기 해줘야하는데

  → 이거 뉴런 하나씩 계산하는게 아니라 한 layer의 뉴런의 weight vector 같은거로로 한번에 처리하면: 자동으로 될듯?

Summary of gradient descent

---

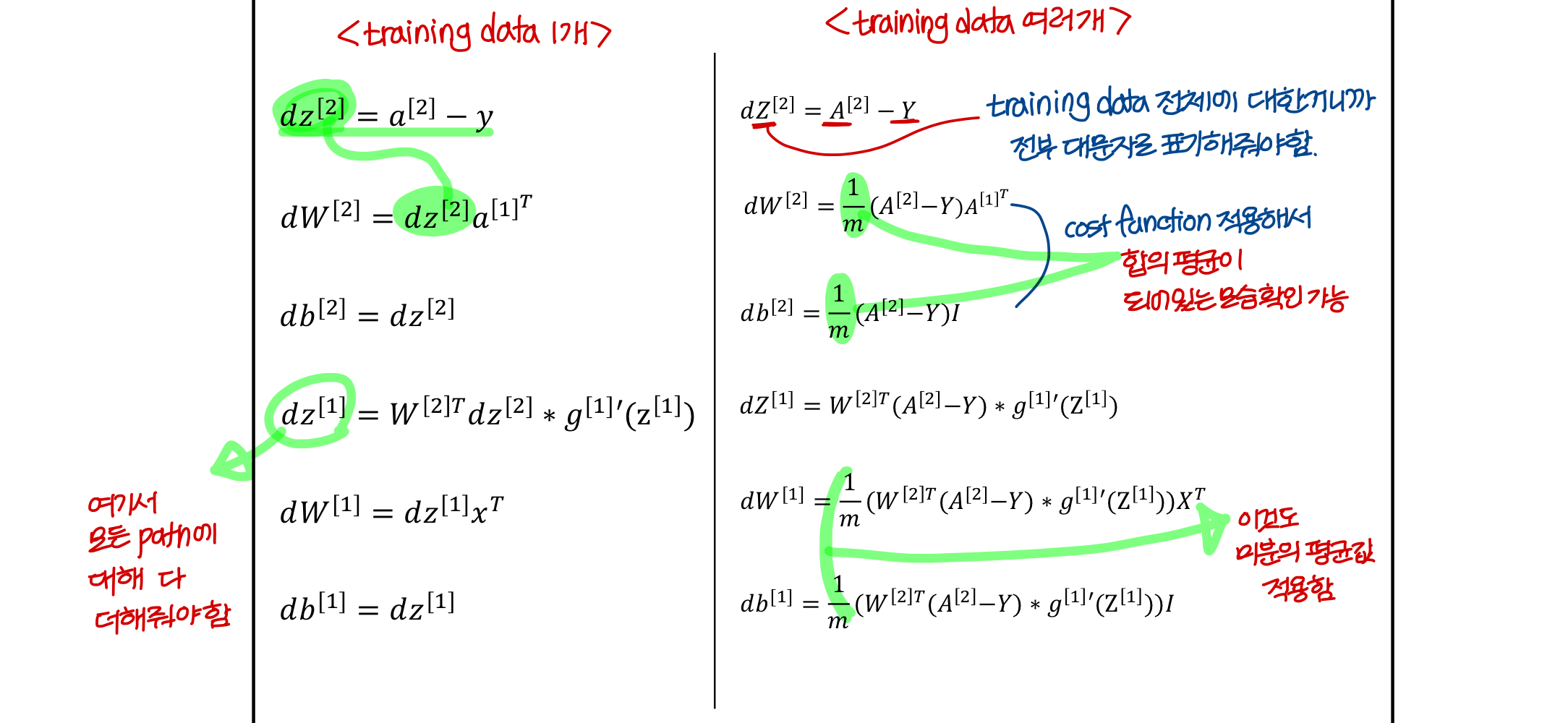
• 방금 본거에서 training data 여러개인 경우에

  $Z, A, Y, W$ 전부 다 matrix로 표현됨

  

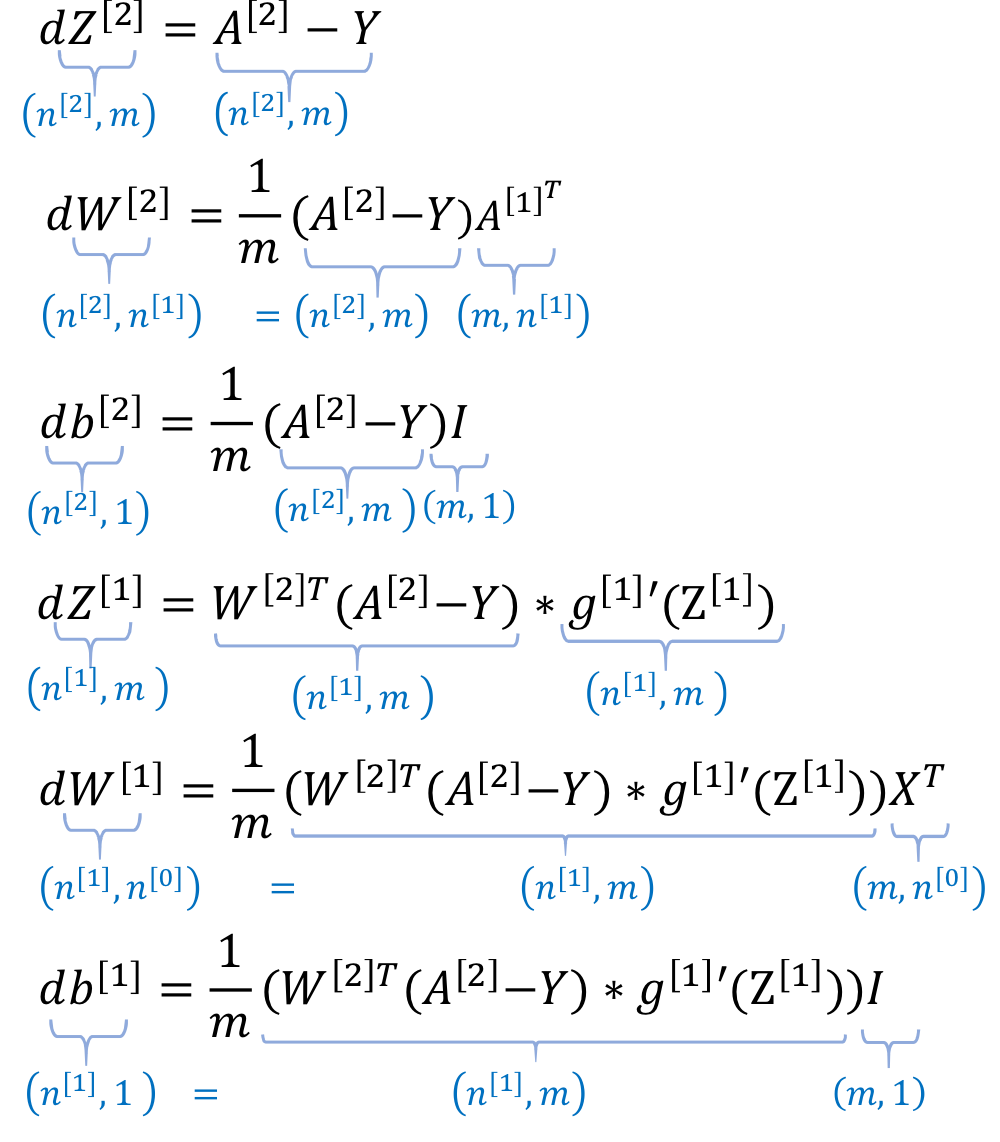
  → 이렇게 굳이 matrix로 표현한 이유가 뭘까?

  왜 matrix operation으로 neural net의 계산을 표현했을까?

  1) 병렬처리가 매우 용이

  2) matrix operation을 잘 이해하면 tensorflow에서 코딩하는데 도움받을 수 있음

Uploaded by N2T