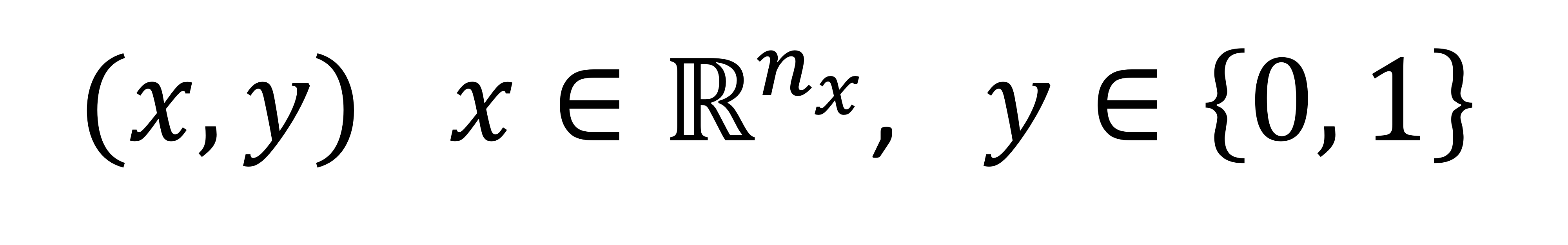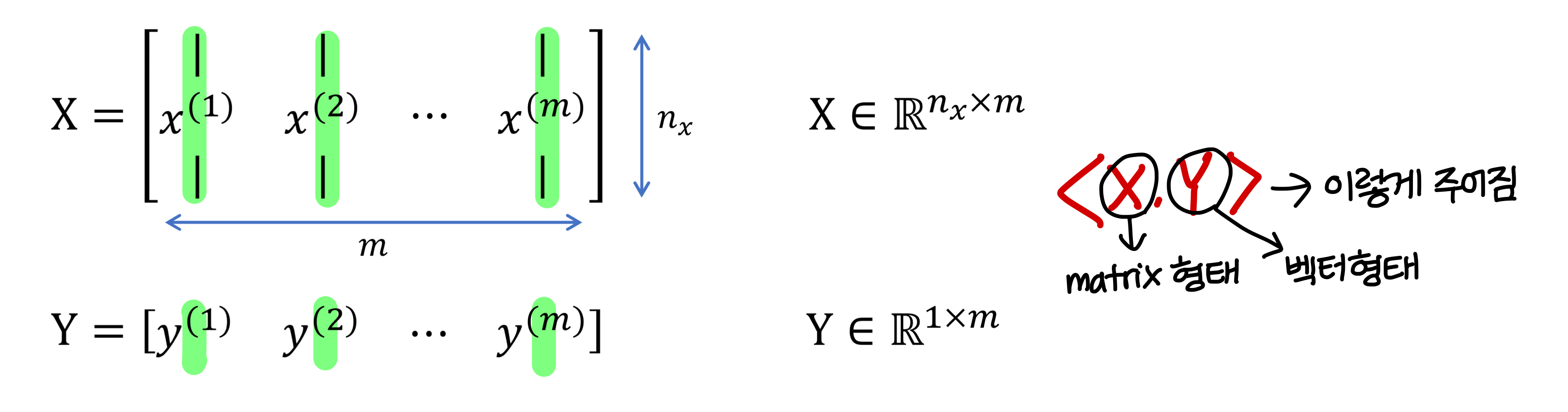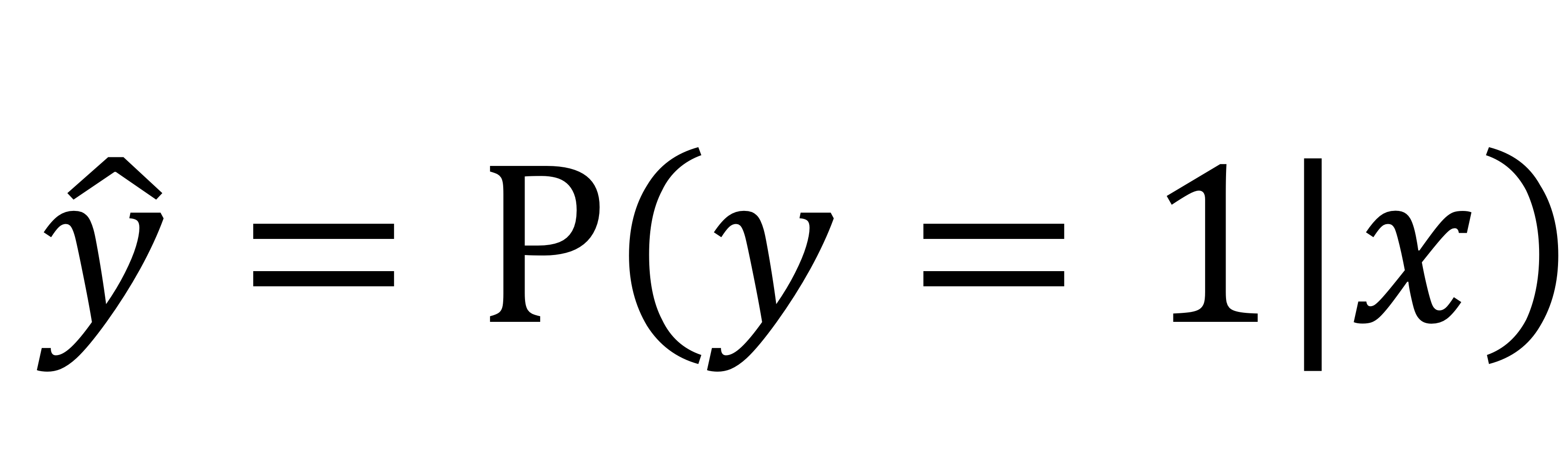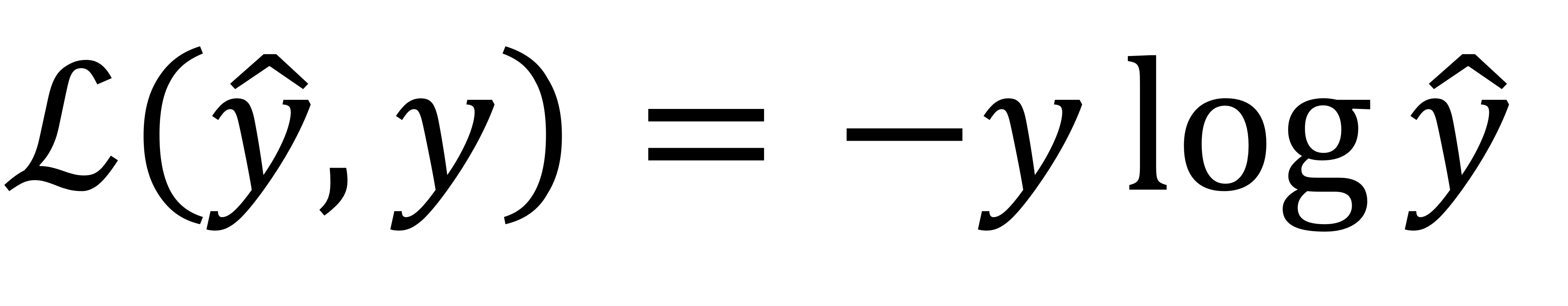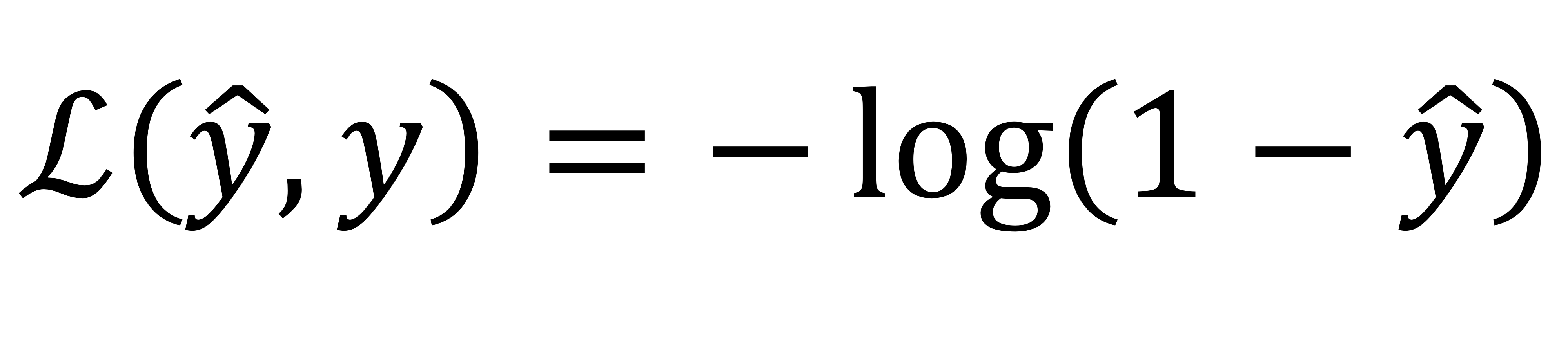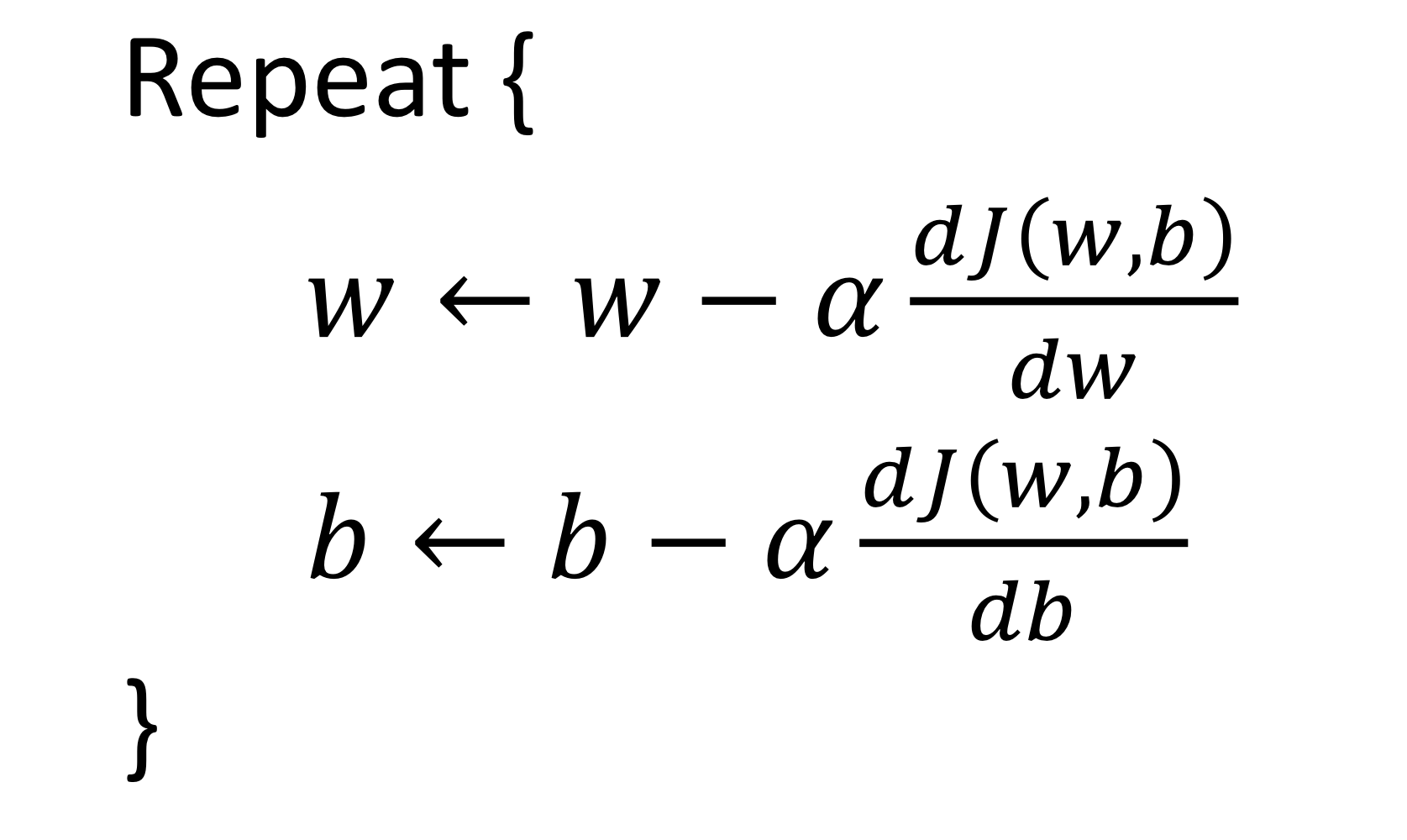딥러닝 수업정리) 02_WramingUp-Logistic Regression

• Logistic Regression: 이건 출력값이 binary 함 (0/1, true/false)

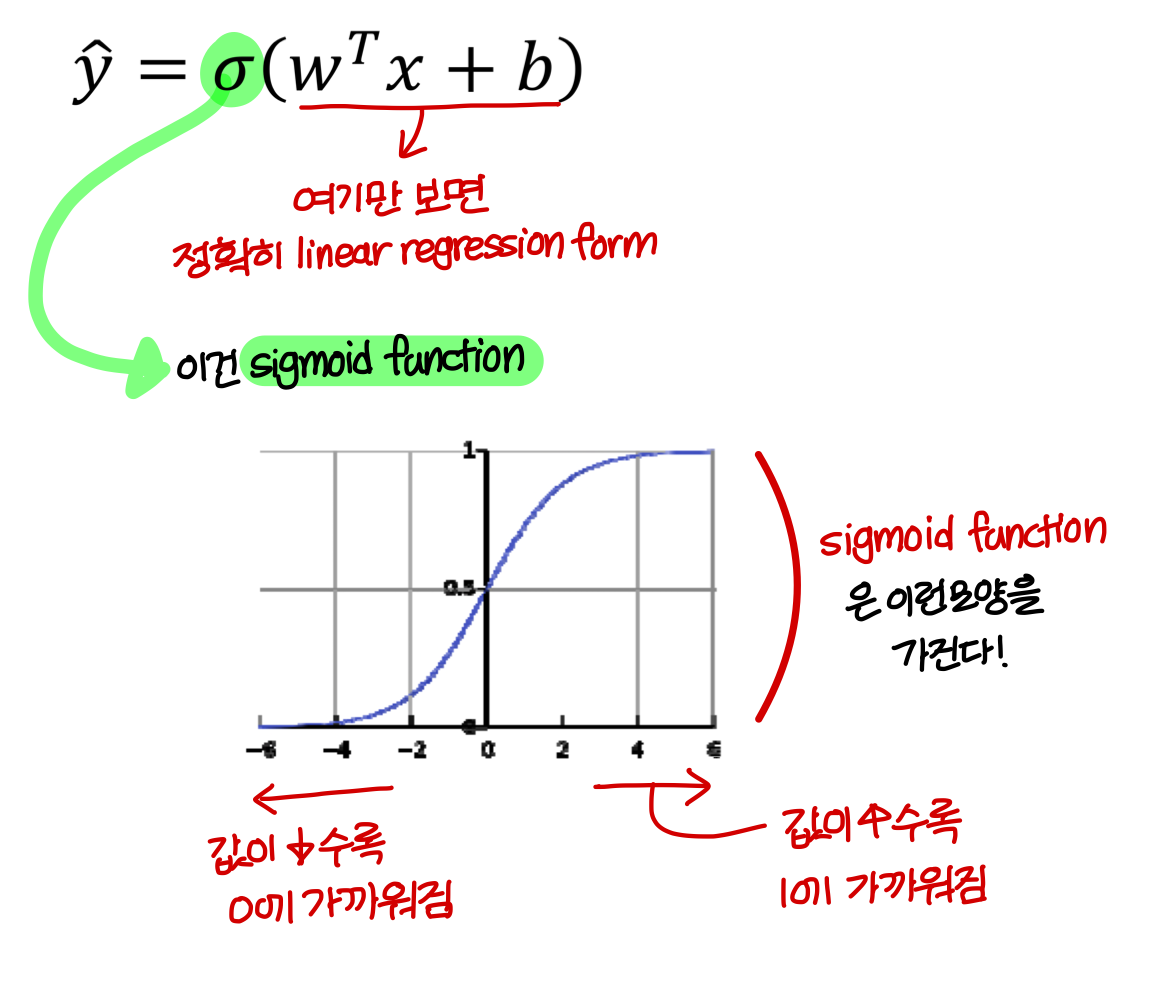
  → 이렇더라도 함수를 modeling할 때는 연속적인 함수를 씀

  → 함수의 출력 값을 확률로 modeling해서 1에 가까우면 true로 판단, 0에 가까우면 false로 판단

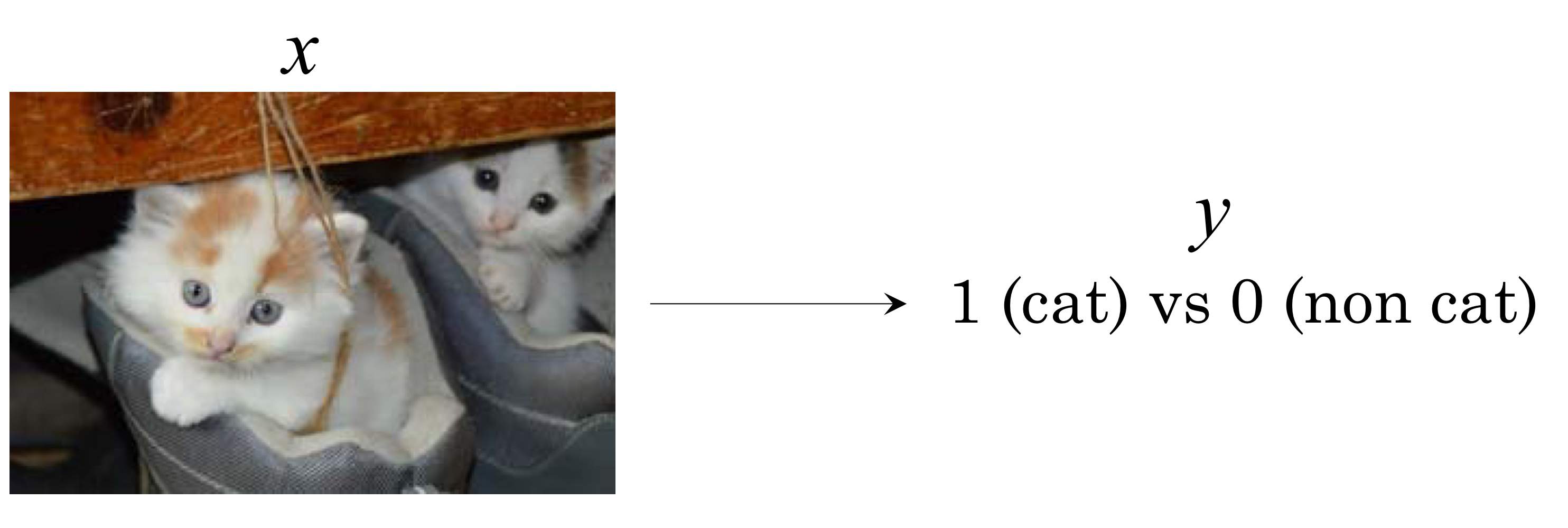
Binary Classification

• neural net model 학습해서 사진 vector 값 주어지면 고양이 맞는지 아닌지 판단해서 결과값을 1 또는 0으로 맞추게 하는 함수를 만듬

  

• 이 함수는 logistic regression 기법으로 modeling할 수 있음

• input은 아주 많은 픽셀들을 하나의 벡터로 만든거

  

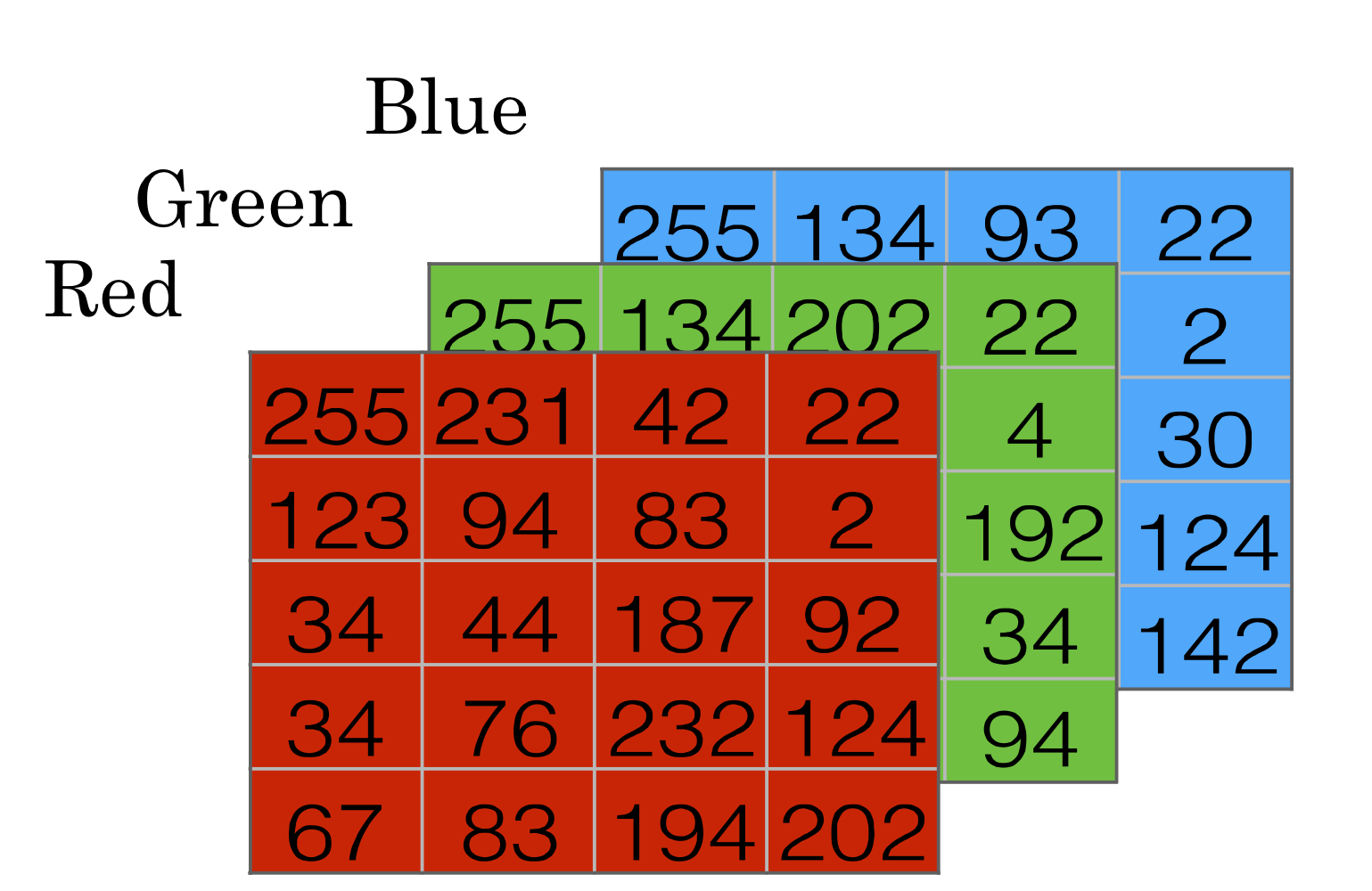
  → 각 숫자가 의미하는건 해당 픽셀의 각 color의 density

  → 만약 사진이 64X64라면 → 사진의 dimension은 64* 64* 3 = 12288

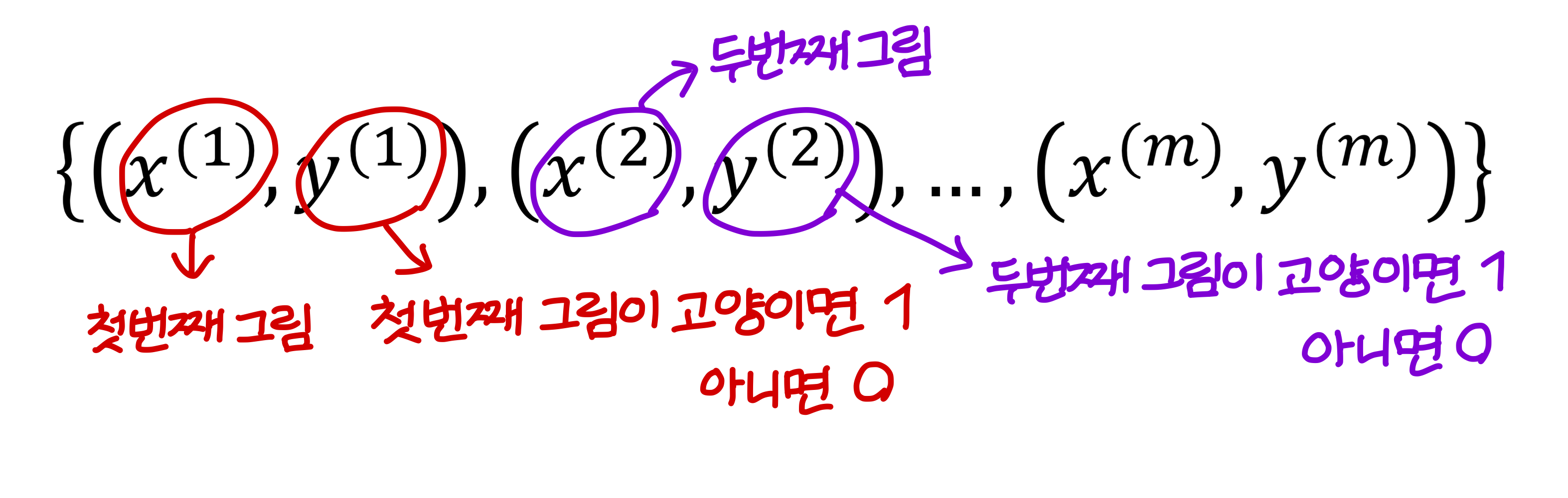
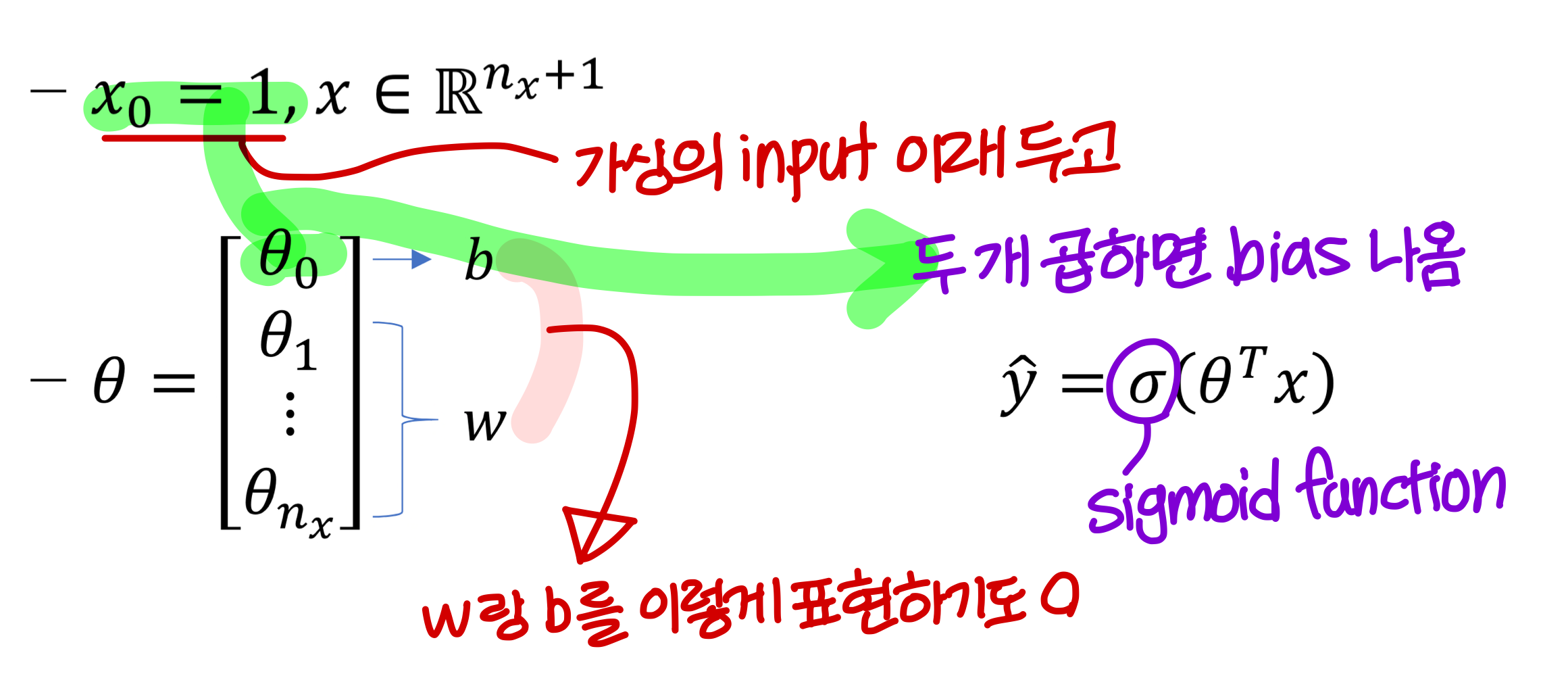
Notation

• Single training data

  

  → x는 하나의 그림 벡터

  → y는 0 또는 1 (고양이면 1, 아니면 0)

• M개의 training data

  

• M개의 training data를 matrix notation 사용해서 더 compact하게 표현 가능

  

Logistic Regression

• 우리가 측정하고자 하는건 이거!

  

  → x(사진)이 들어왔을 때 y = 1(고양이)일 확률을 추정하는 함수 모델을 만들거임

  → y hat은 확률이니까 0 ≤ y hat ≤ 1

---

• Model의 parameter: weight, bias

• Model의 output: y hat (activation function을 통과한 값)

  

💡

결론적으로, logistic regression은 linear combiation으로 나타나는 기존의 linear regression에 sigmoid function이 적용된 형태

---

Linear Regression vs Logistic Regression

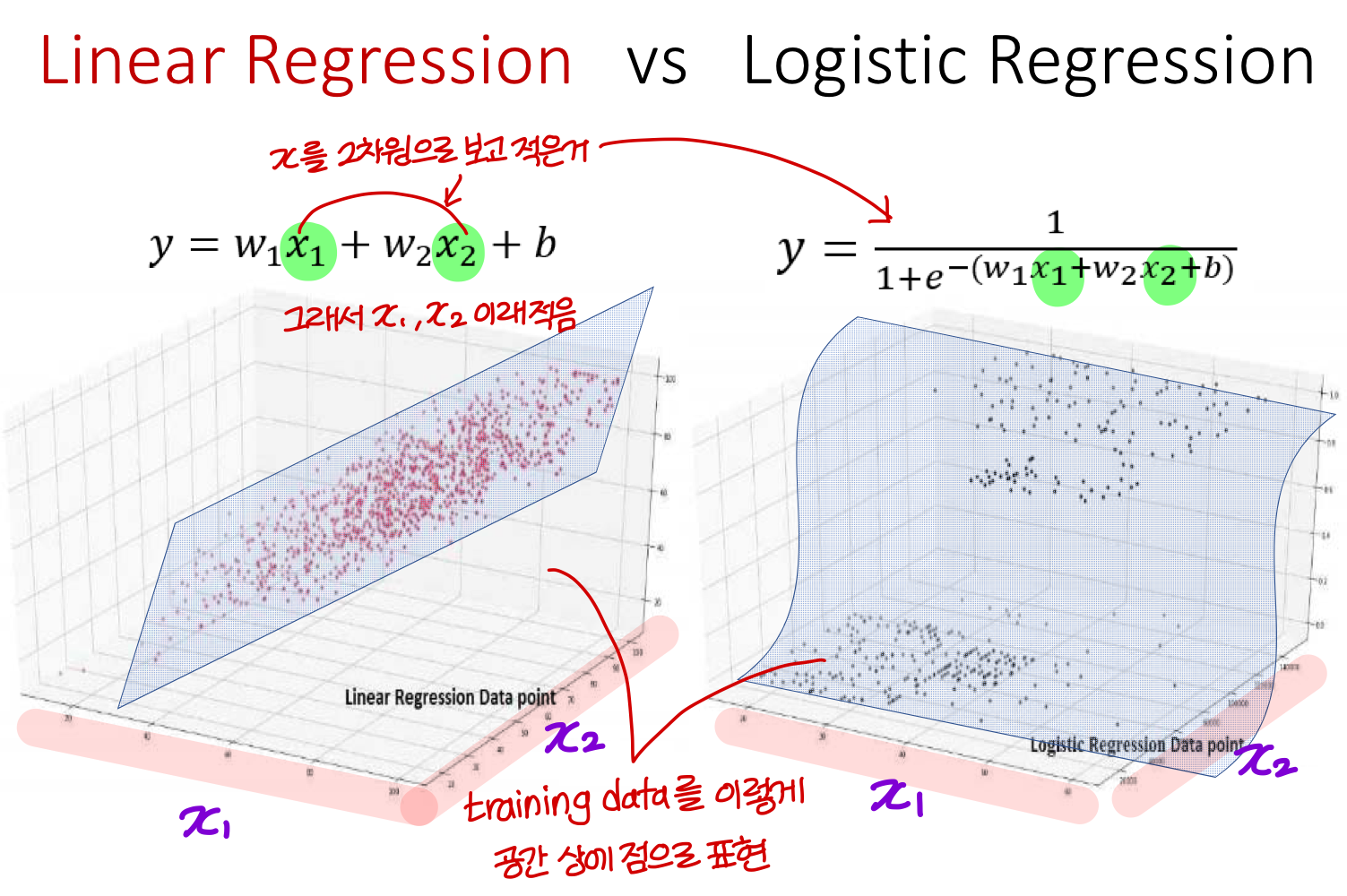
• Linear Regression

  공간상의 training data 제일 잘 표현하는 hyper plan은 평면

  → 즉, training data를 잘 표현하는 linear regression 함수는 공간 상에서 평면으로 표현됨

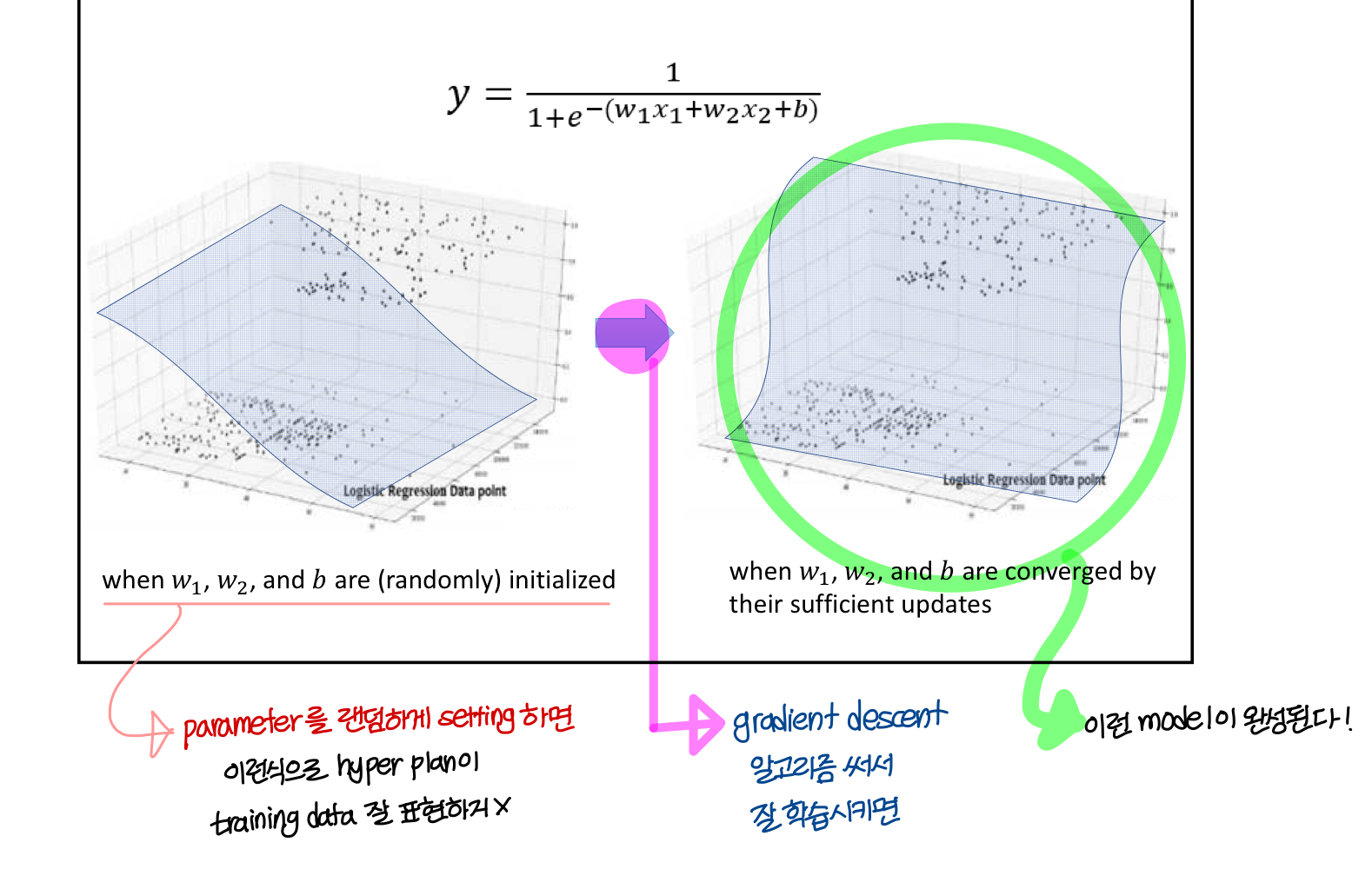
• Logistic Regression

  공간상의 training data 제일 잘 표현하는 hyper plan은 S자 곡선

  → 즉, training data를 잘 표현하는 logistic regression 함수는 공간 상에서 S자로 표현됨

---

다시 돌아와서

Logistic Regression

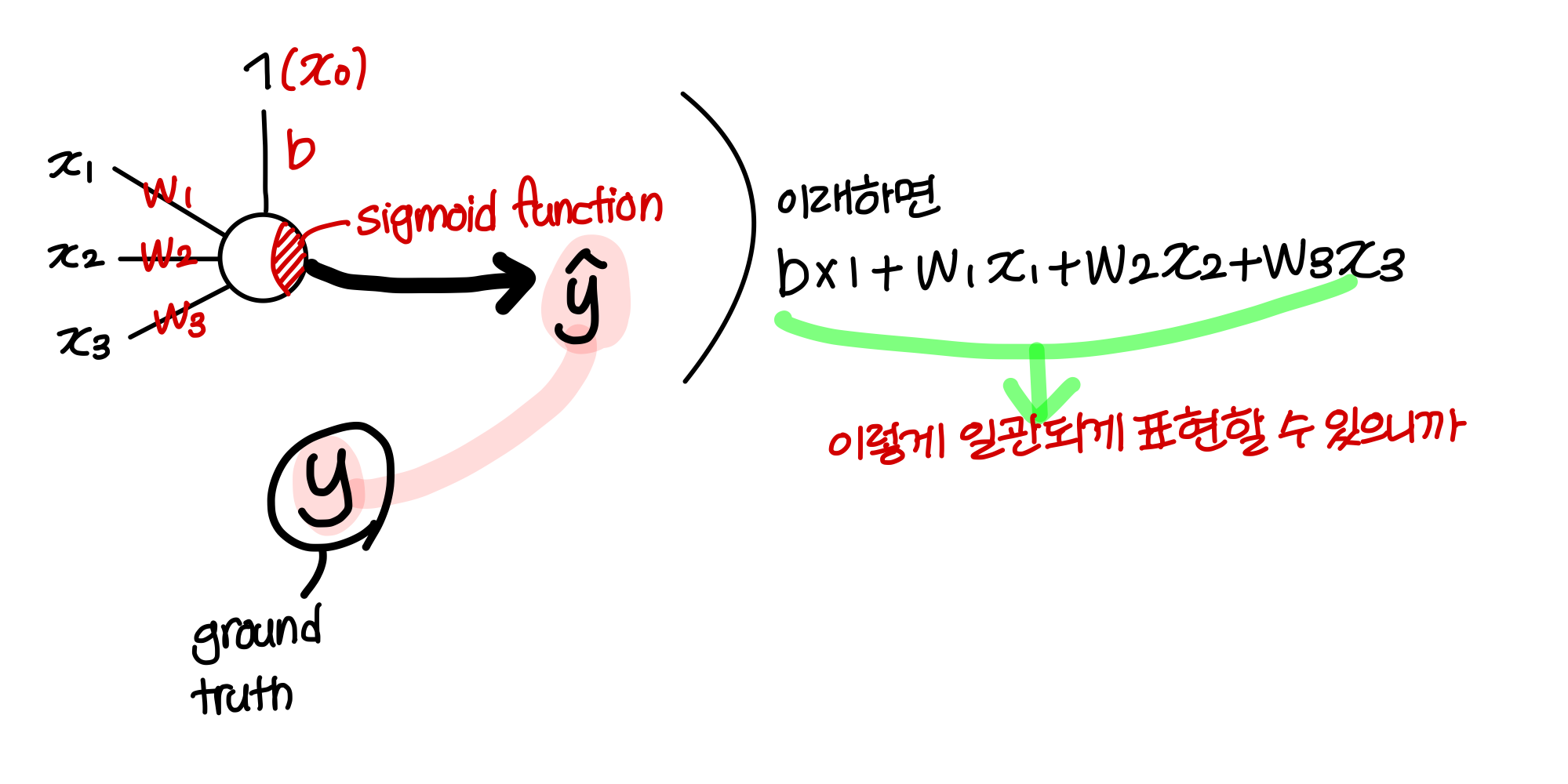
• 이걸 배우는 이유는 artificial neural net의 뉴런 하나가 logistic regression을 표현하는 model임

  

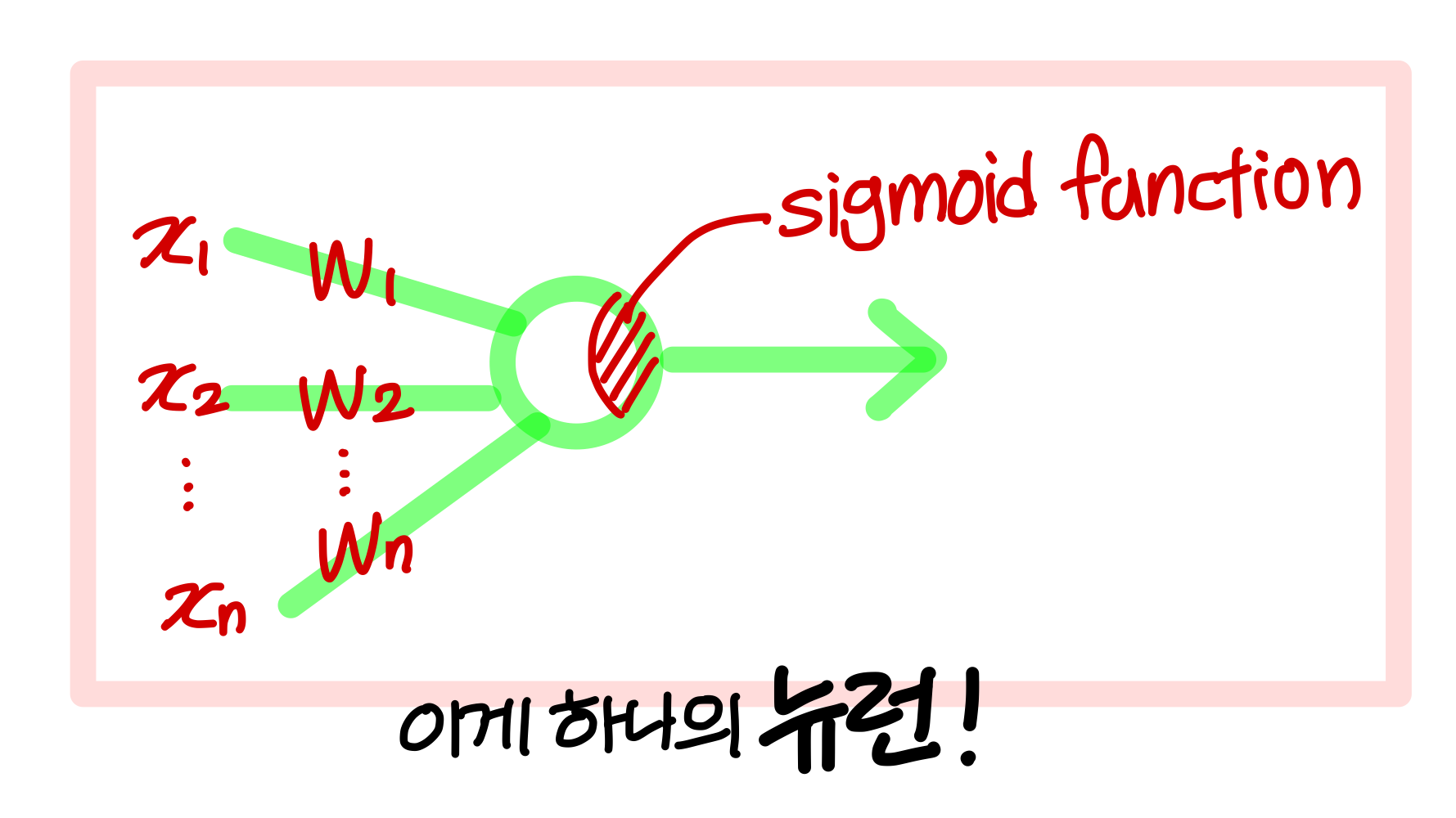
  → 여러 뉴런들을 여러 층으로 결합하게 되면 이게 artificial neural net

• logistic regression의 목표

  → $w$와 $b$를 학습시켜서 추정되는 y hat 값이 실제 y 값과 최대한 같아지도록 학습시키는거

• Notational convention

  

---

→ y와 y hat 이 두 값의 차이를 표현하는 함수를 loss function 이라고 한다.

---

Logistic Regression Cost Function

• Loss(error) function

  

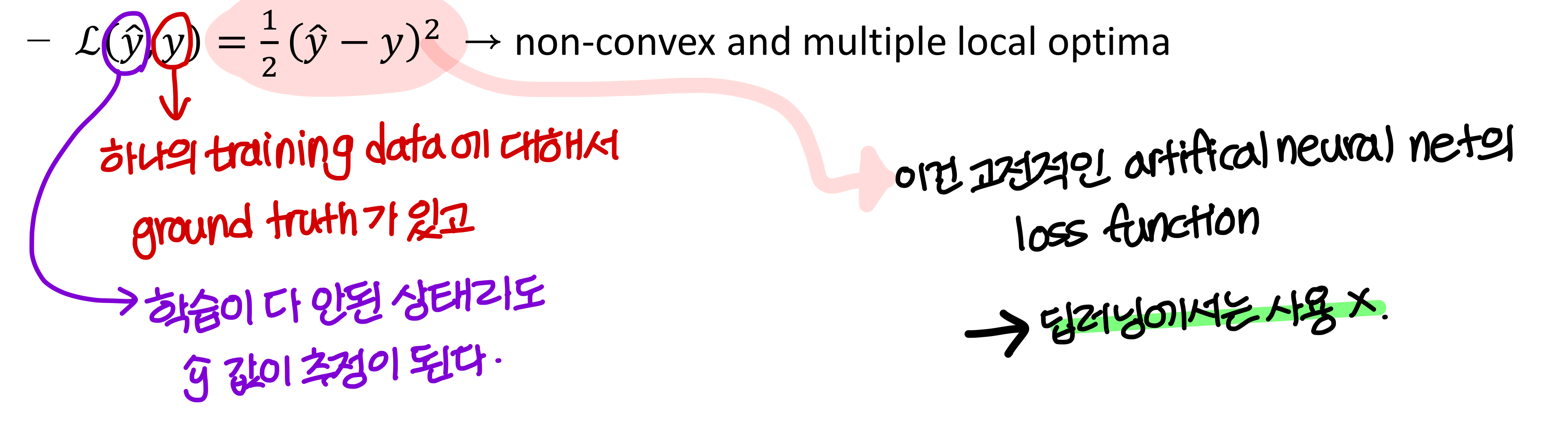
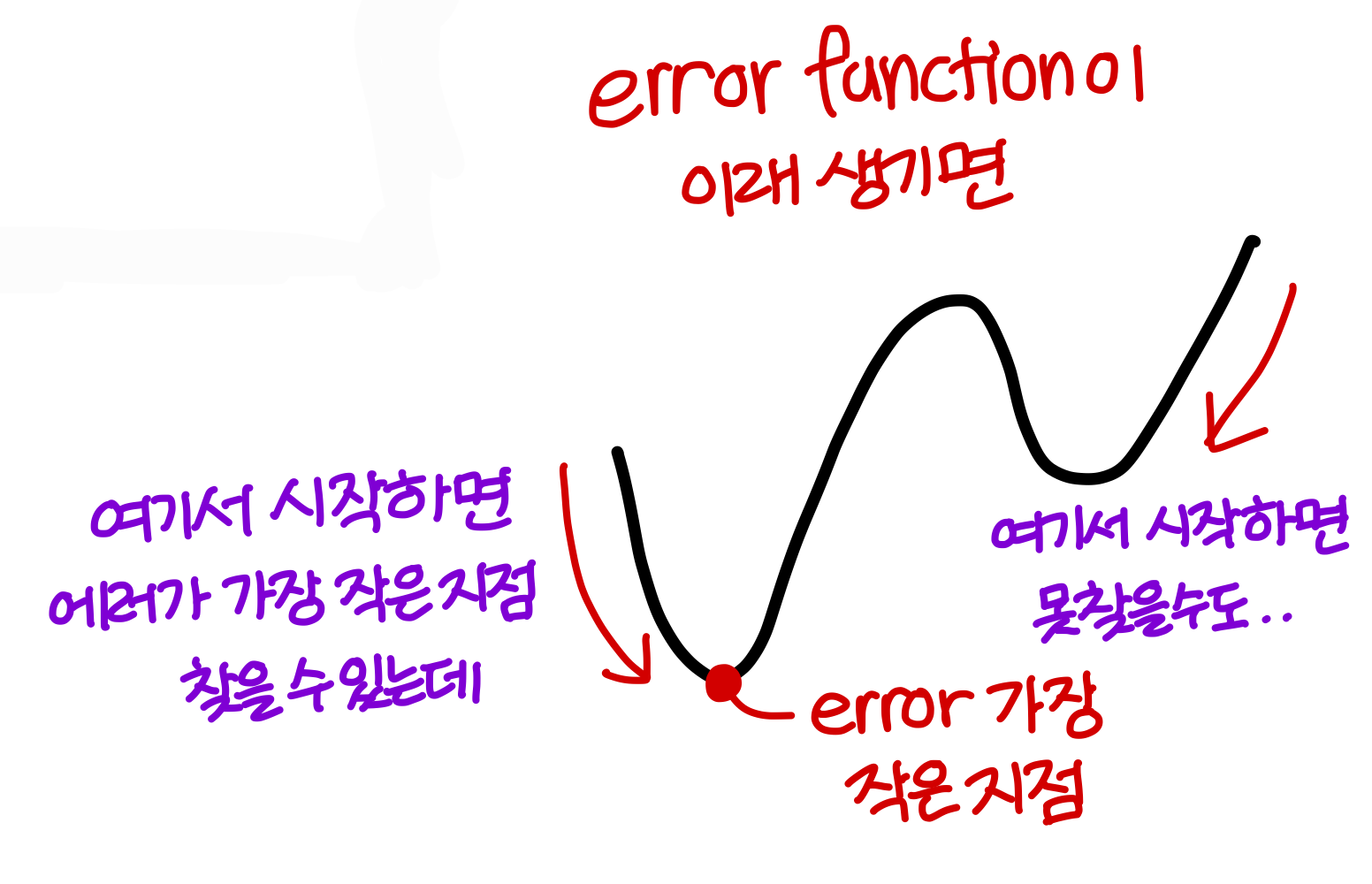
  → 이렇게 하면 결과가 non convex function이 된다.

  → 그리고 (한번 볼록한) 간단한 형태가 아니라 복잡한 형태의 함수가 된다.

  그렇게 되면 다음과 같은 문제 생길 수 있음

  

  ---

  💡

  그래서 딥러닝에서는 loss function으로 cross entropy loss 사용!

  

  • 앞에 - 붙어있음! (ground truth)log(추정값) 이런 형태
  • 이 loss function을 사용했을 때

    → 고양이라면 y = 1이니까

    

    : 이 부분만 남게 된다. loss function 값이 작을수록 좋은거니까 y hat이 1에 가까워질수록 좋음

    → 고양이가 아니라면 y = 0이니까

    

    : 이 부분만 남게 된다. loss function 값이 작을수록 좋으니까 y hat이 0에 가까워질수록 좋음

  💡

  결론적으로 이 cross entropy loss를 최소화시키려면 y hat과 y 값이 같아져야한다.

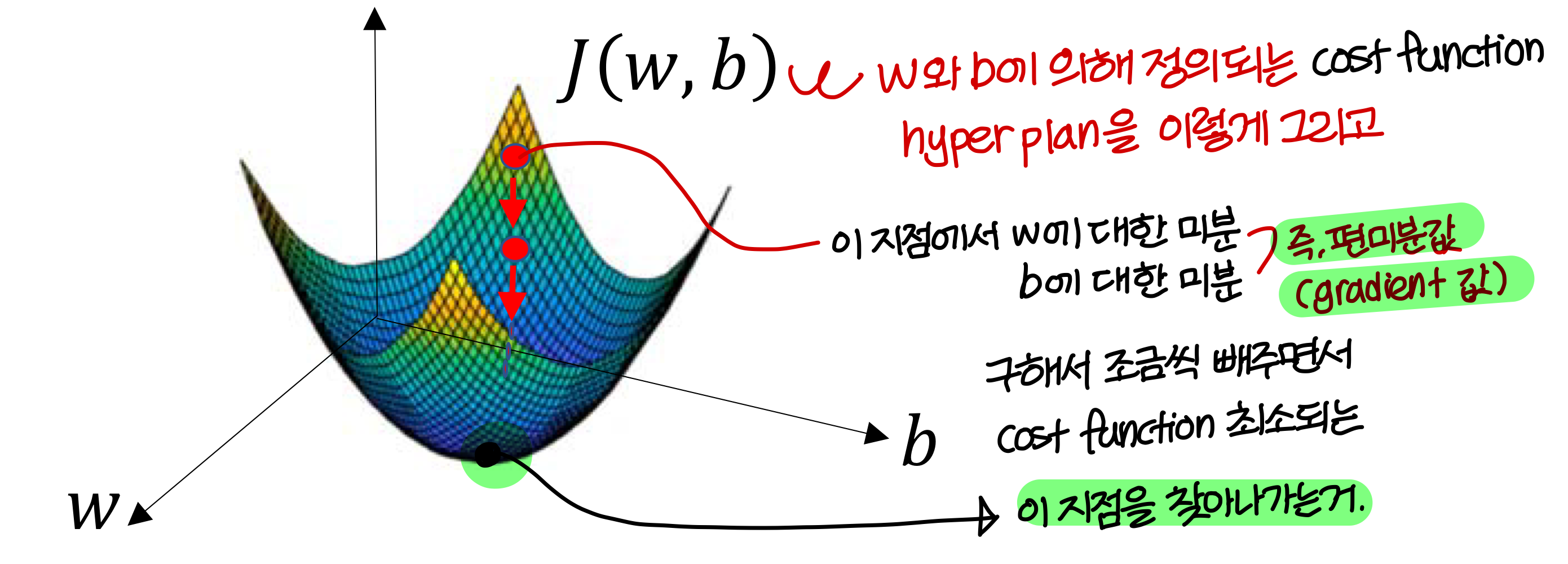
Cost function

: loss function 값을 training data에 대해 다 계산해서 평균값낸거

💡

표기 주의! Cost function이라고 해서 C로 표현하지 않을까 했는데 J임!

→ 이 cost function 값 $J(w, b)$를 최소화시키는 $w$와 $b$를 찾아낼거임

→ 이걸 어떻게 찾을 수 있을까?

---

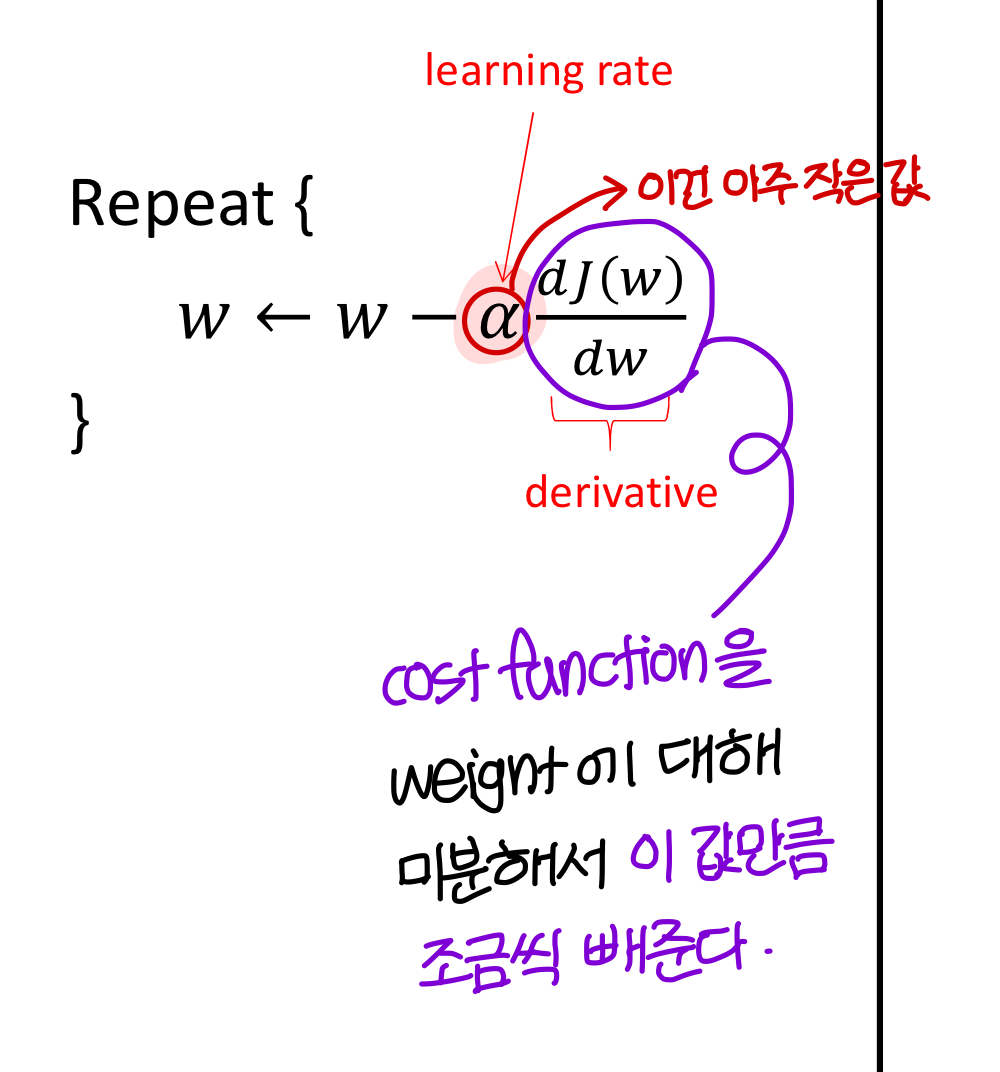
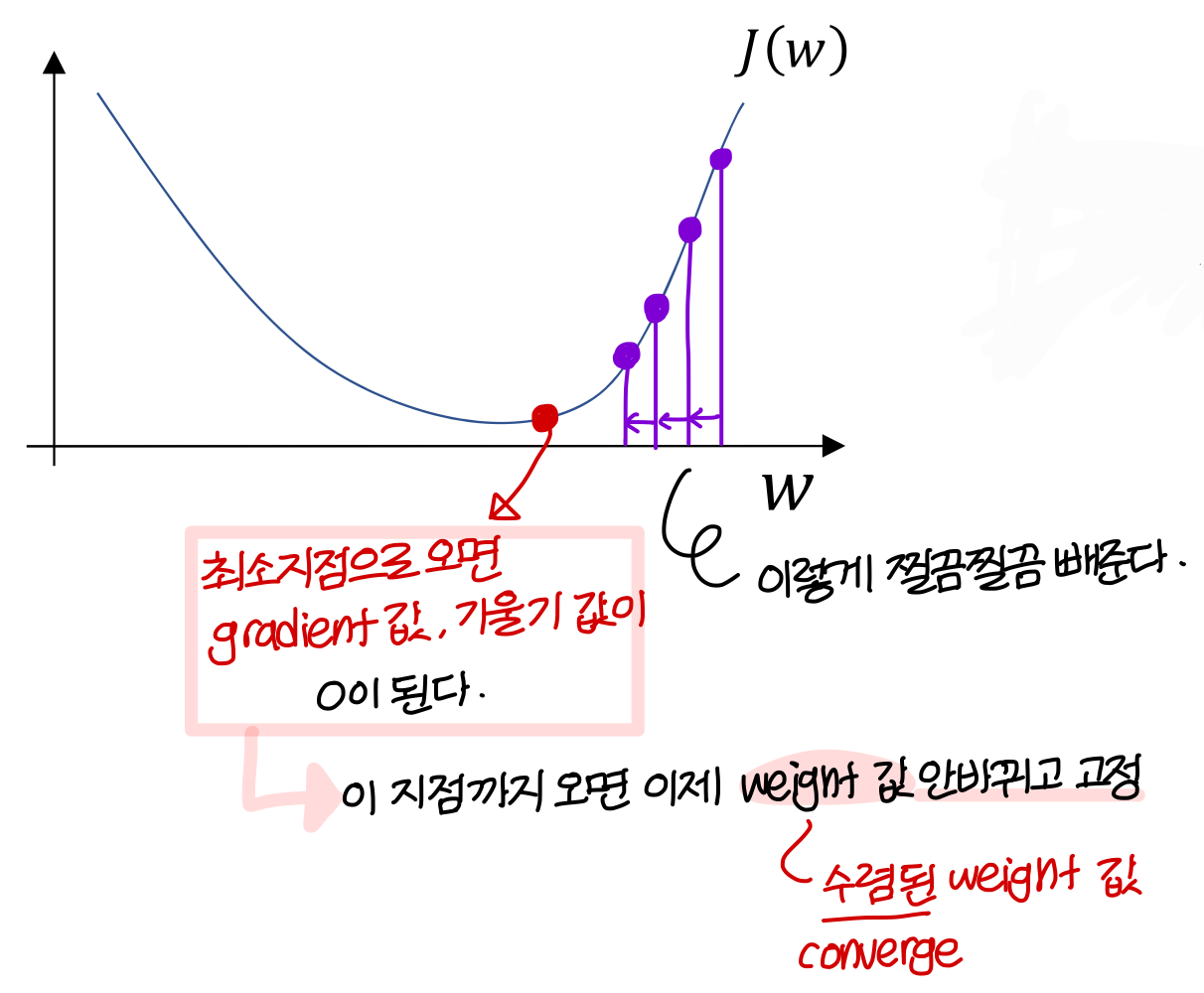
Gradient Descent(하강)

• 2차원 기준으로 $w$에 대해 살펴보자

• $b$ 에 대해서도 똑같은 방법을 적용함

  즉 다음을 반복하게 됨

  

💡

즉 $w^*$, $b^*$(수렴된 $w$와 $b$)가 학습된 model의 실체

---

Computation Graph

💡

그런데 neural net과 같은 network 구조에서 gradient를 어떻게 구하지? → 이걸 이해하기 위해서 computation graph를 이해해야함!

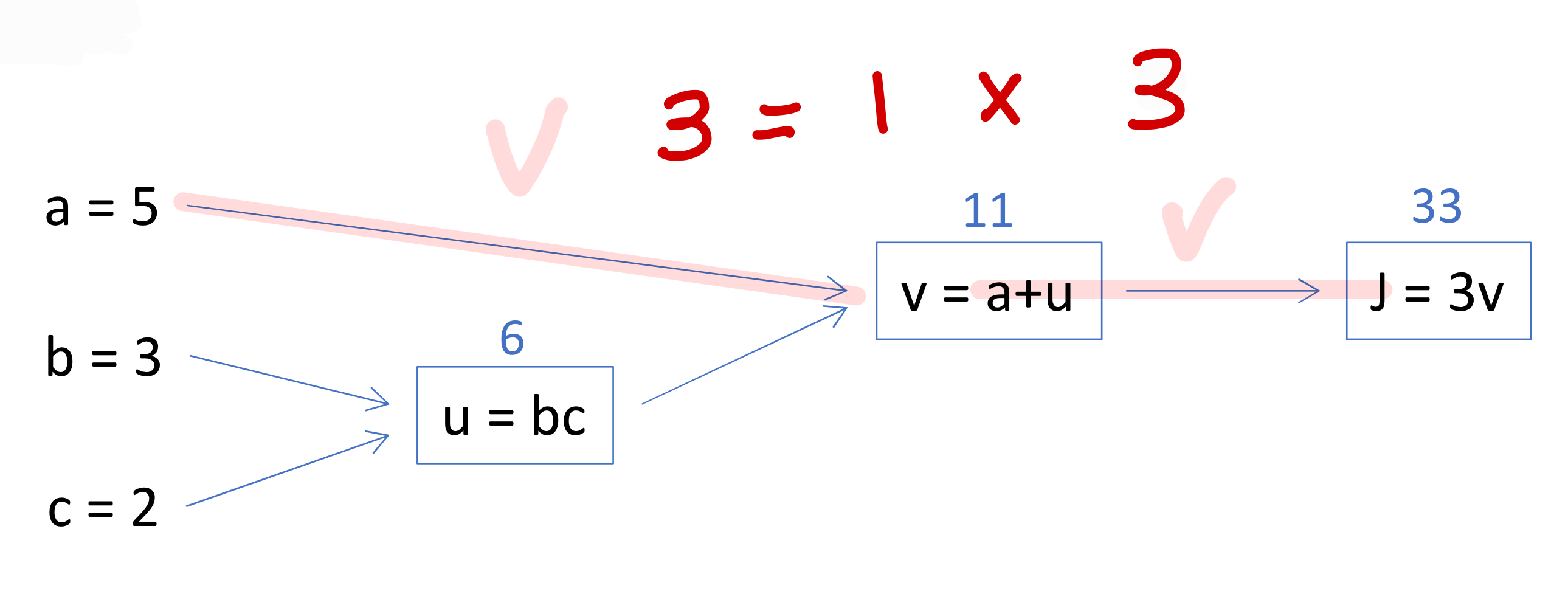
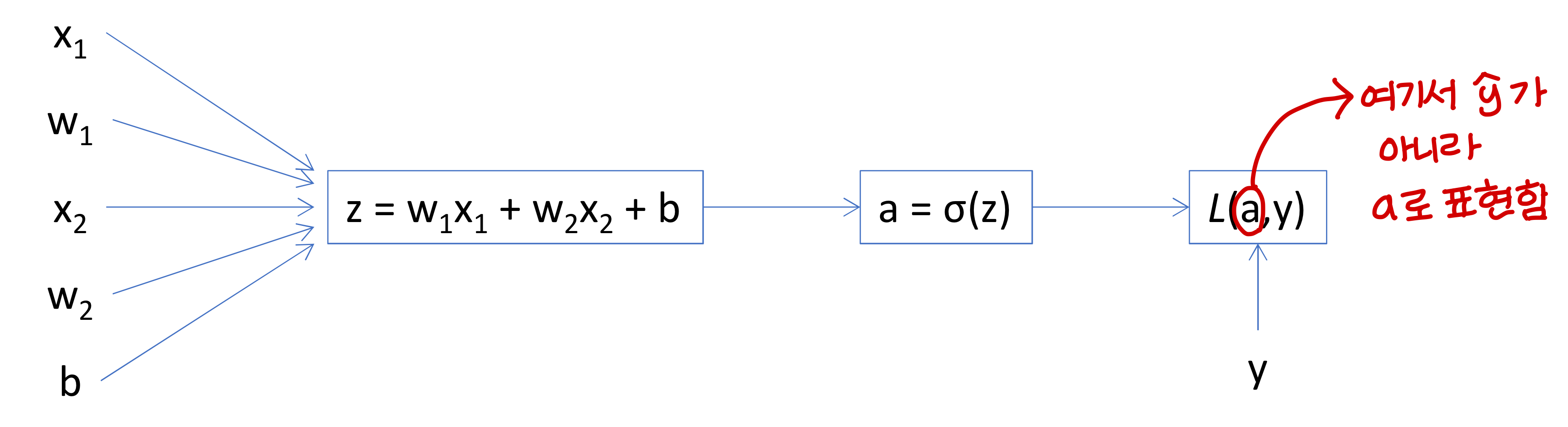
• 3개의 variable을 가진 $J$라는 cost function을 compute 해볼거임

• $J(a, b, c) = 3(a+bc)$

  → 이걸 3개의 step을 밟아서 계산할 수 있음

  1) $u = bc$

  2) $v = a+u$

  3) $J = 3v$

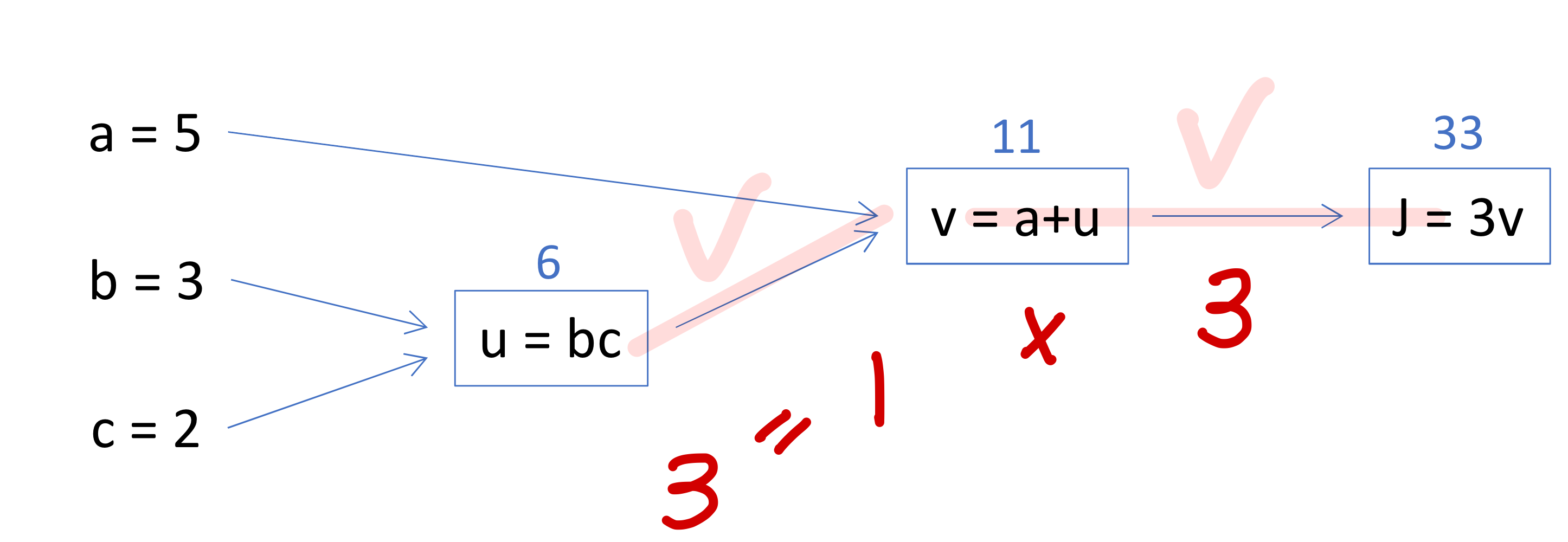
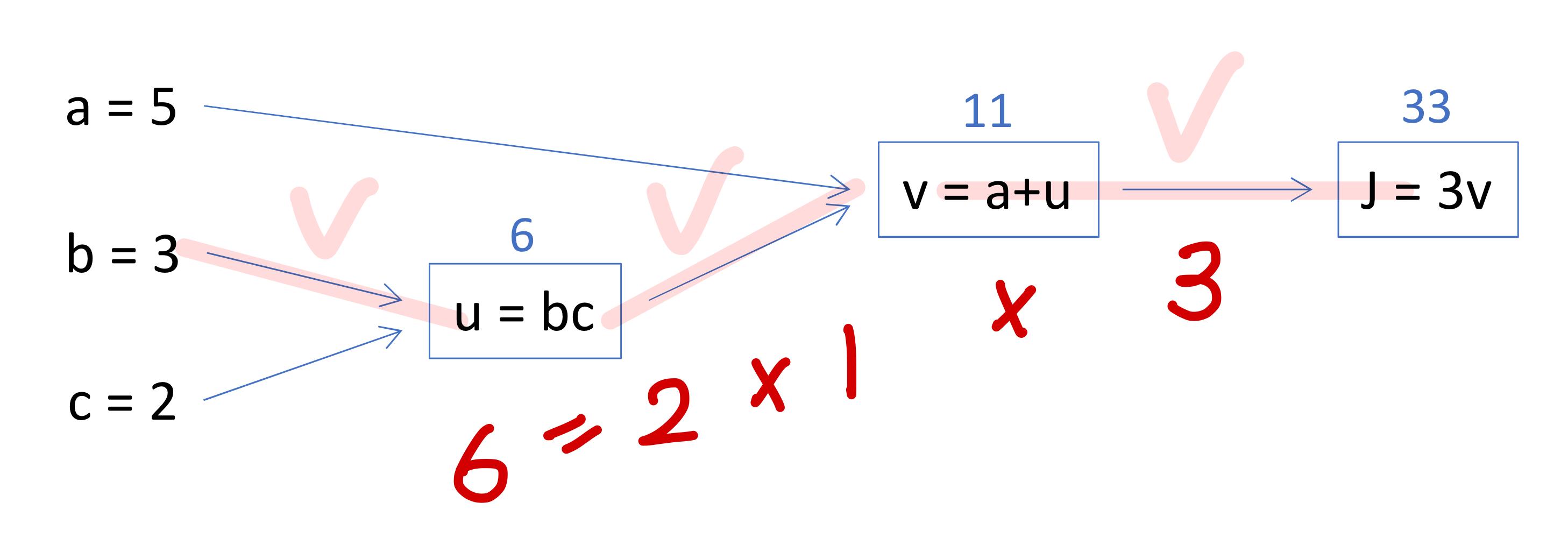
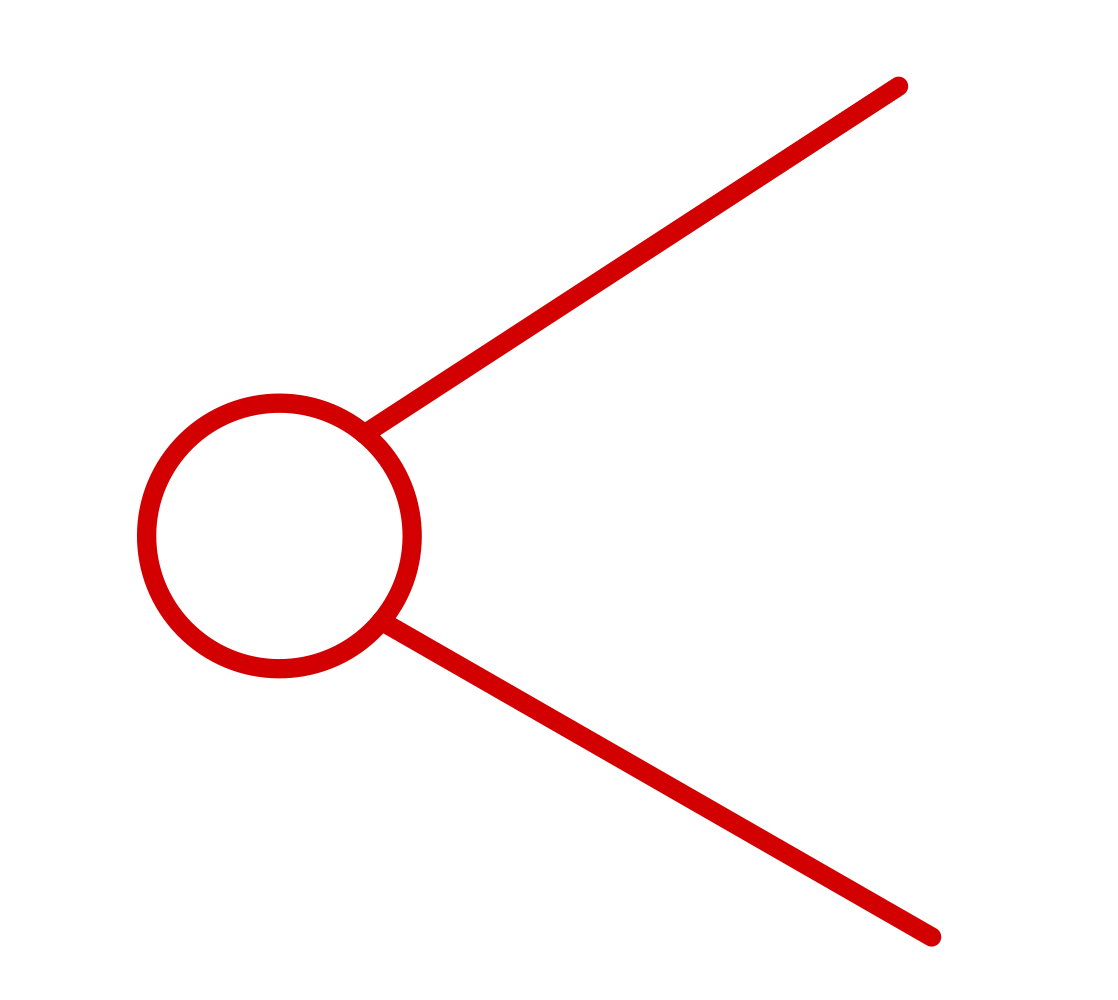
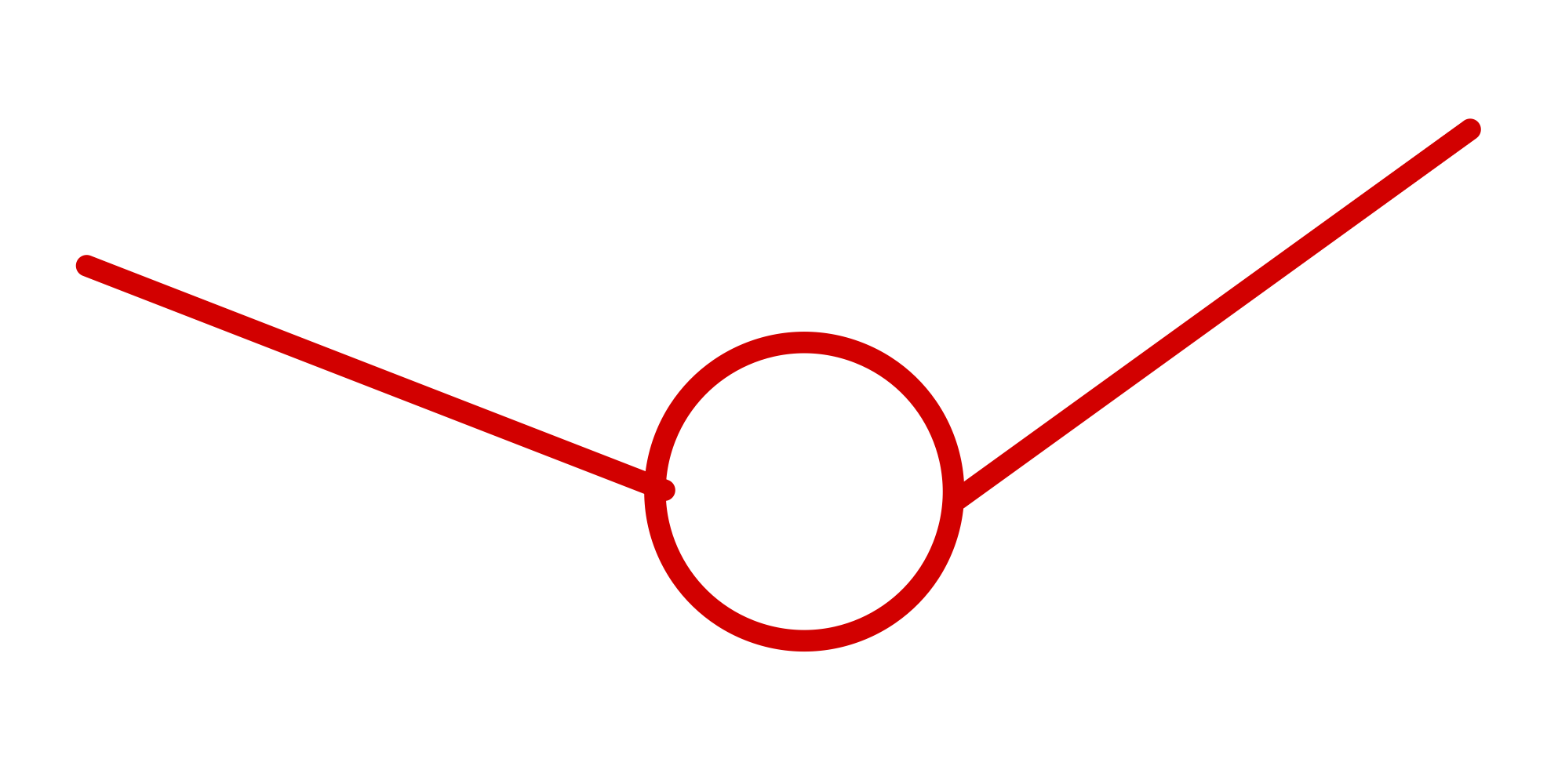
  → 이걸 computation graph로 표현하면

  

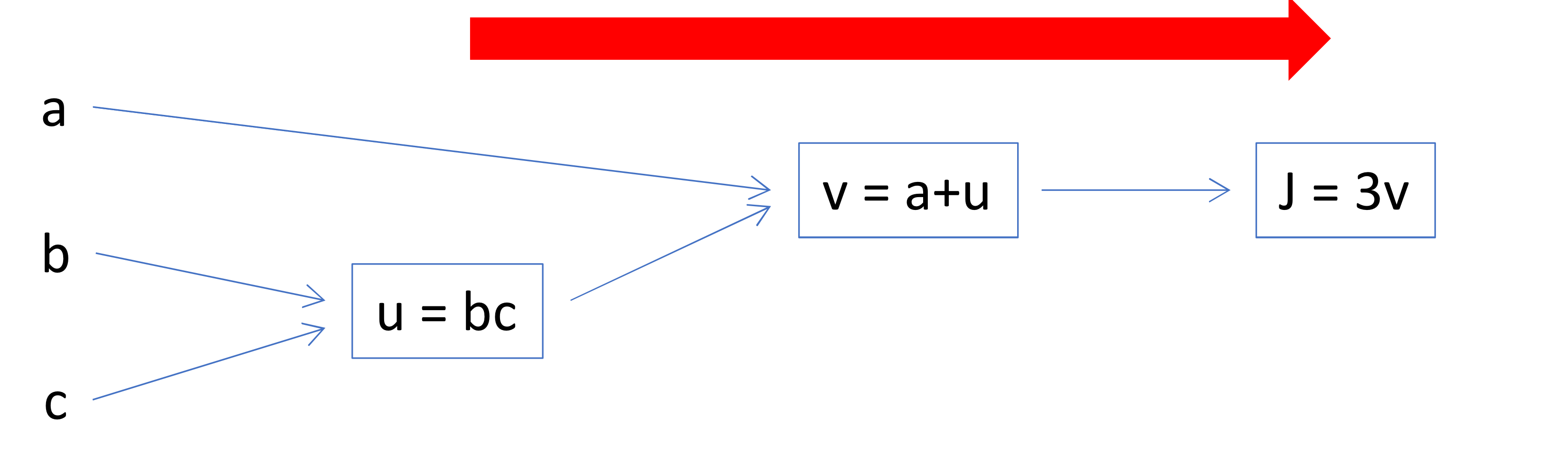
  : cost function을 계산하기 위해서는 Forward pass를 해야함

  : 그리고 gradient를 구하기 위해서(편미분을 하기 위해서는) Backward pass를 해야함

Derivatives with a Computation

→ 이렇게 일단 구해놓고

• $dJ/da$ 구할 때는

  

  → 이렇게 경로에 있는거 다 곱하고

• $dJ/du$ 구할 때는

  

  → 이렇게 경로에 있는거 다곱하고

• $dJ/ db$ 구할 때는

  

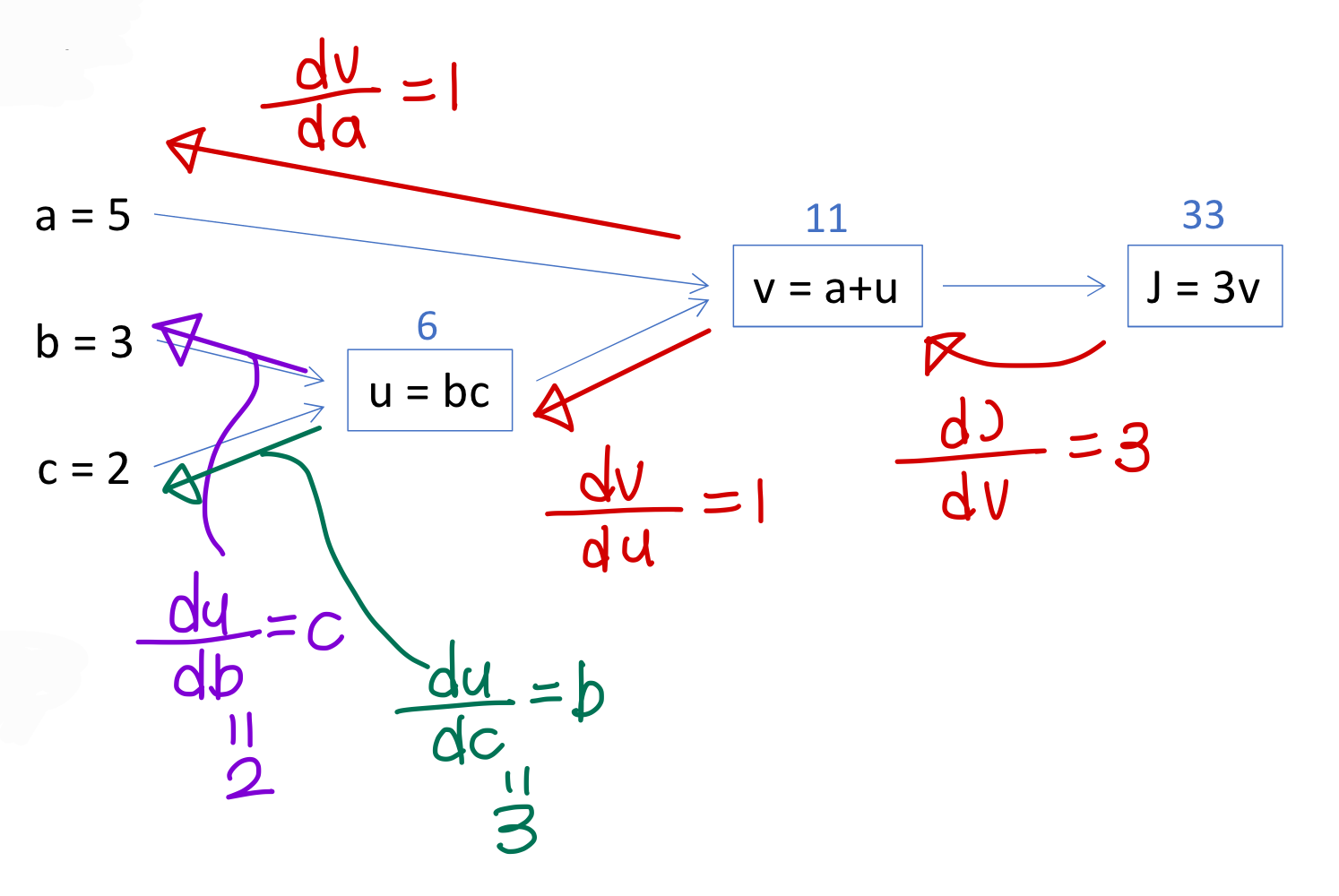
  → 이렇게 경로 다 있는거 곱하고

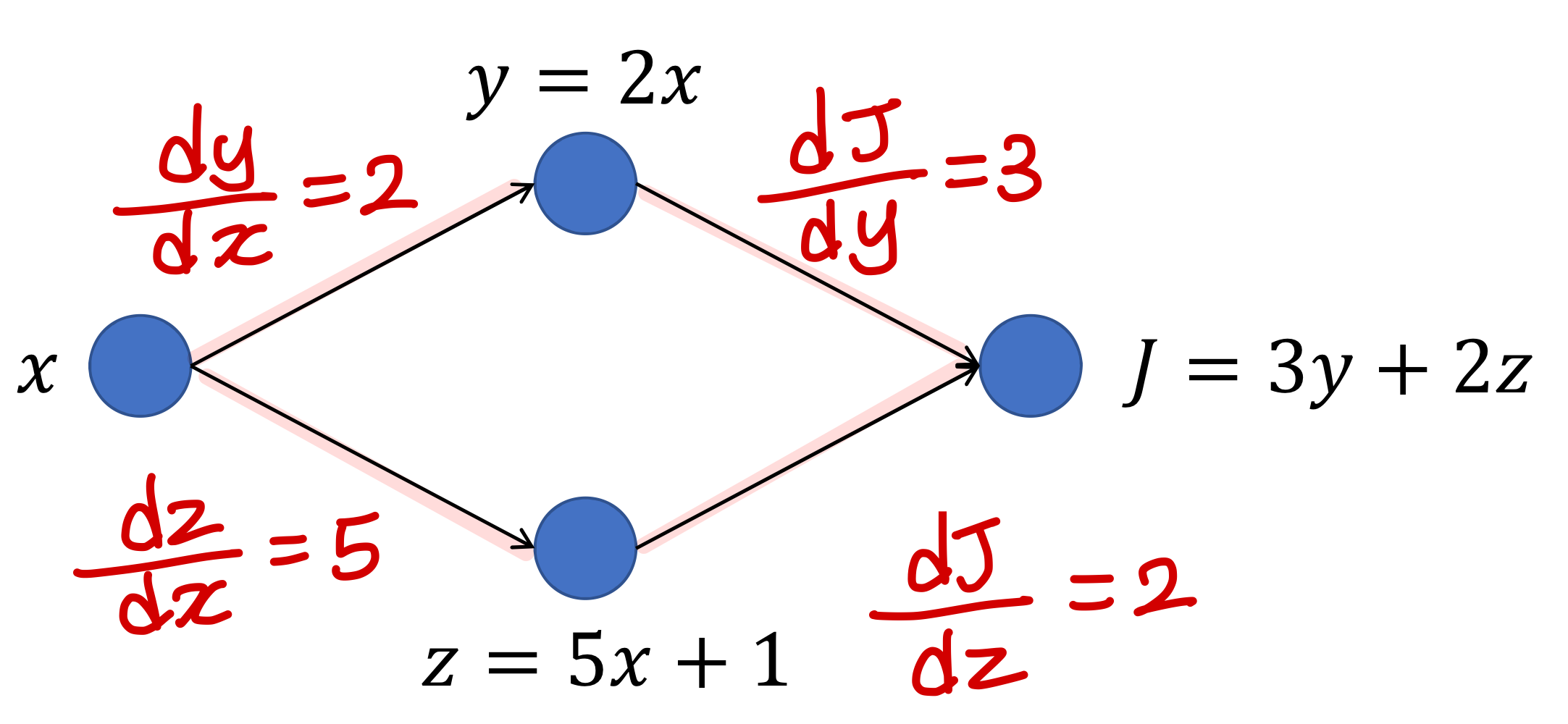
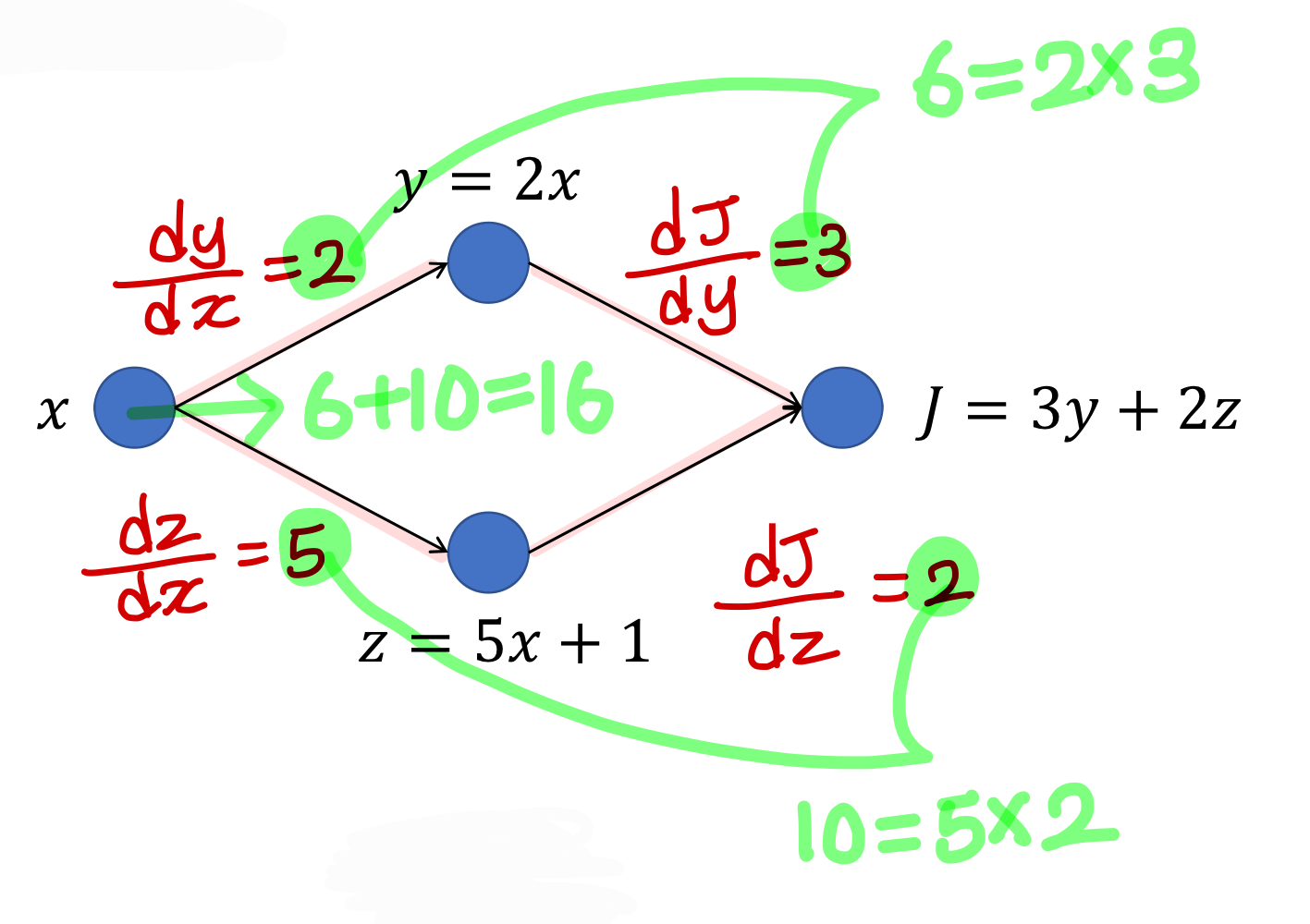
Exercise

💡

근데 이렇게 경로가 나누어졌다가 합쳐지는 경우에는 어떡하지?

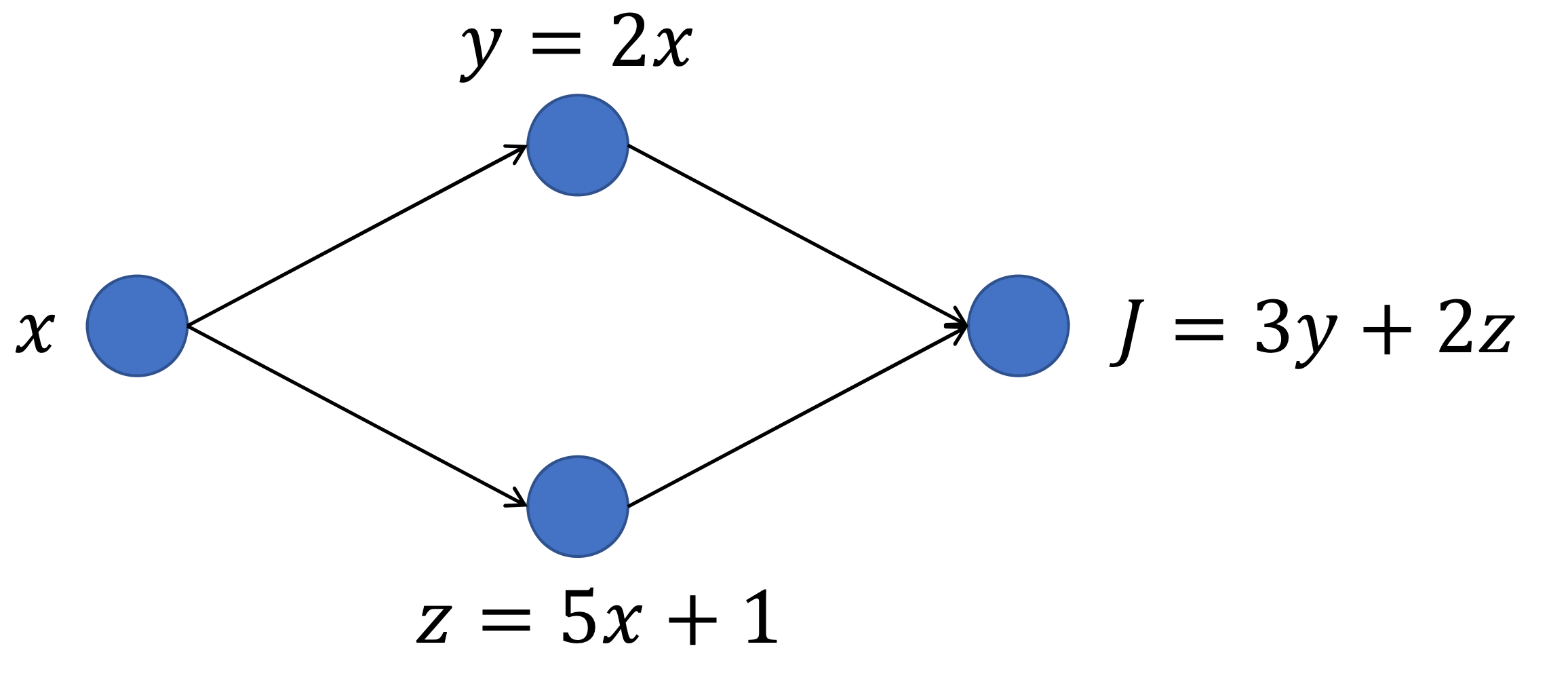
→ 이 경우에는 경로가 나누어졌다가가 합쳐진다

→ $dJ/dx$를 다음과 같이 구한다

: 일단 이렇게 구해놓고

: 각 path 별 미분값을 더해버림

→ 그냥 우리 미분할 때 이러는거랑 똑같다고 보면 됨

Gradient 계산하는 결론

→ 모이는 곳은 더하고

→ 지나가는 곳은 더한다

Logistic Regression Derivatives

• Logistic regression 계산과정 다음과 같음

  

• Logistic regression을 computation graph로 표현하면

  

💡

이제 $w$와 $b$에 대해 미분을 진행할거임

1) da 구하기

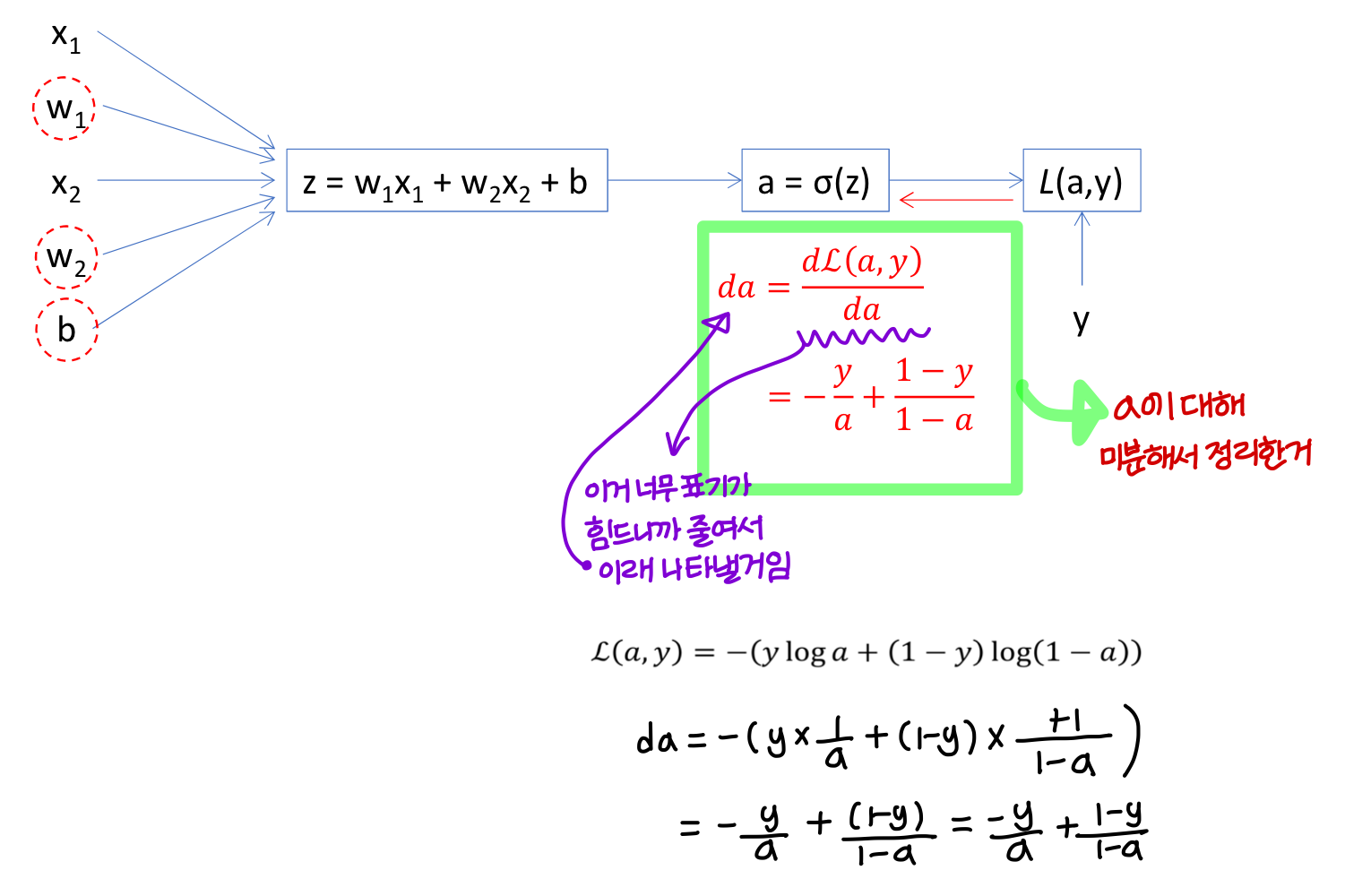
2) dz 구하기

💡

이거 꼭 기억하기! sigmoid 함수를 $a$ 라고 했을 때 이걸 미분하면 $a(1-a)$가 나옴

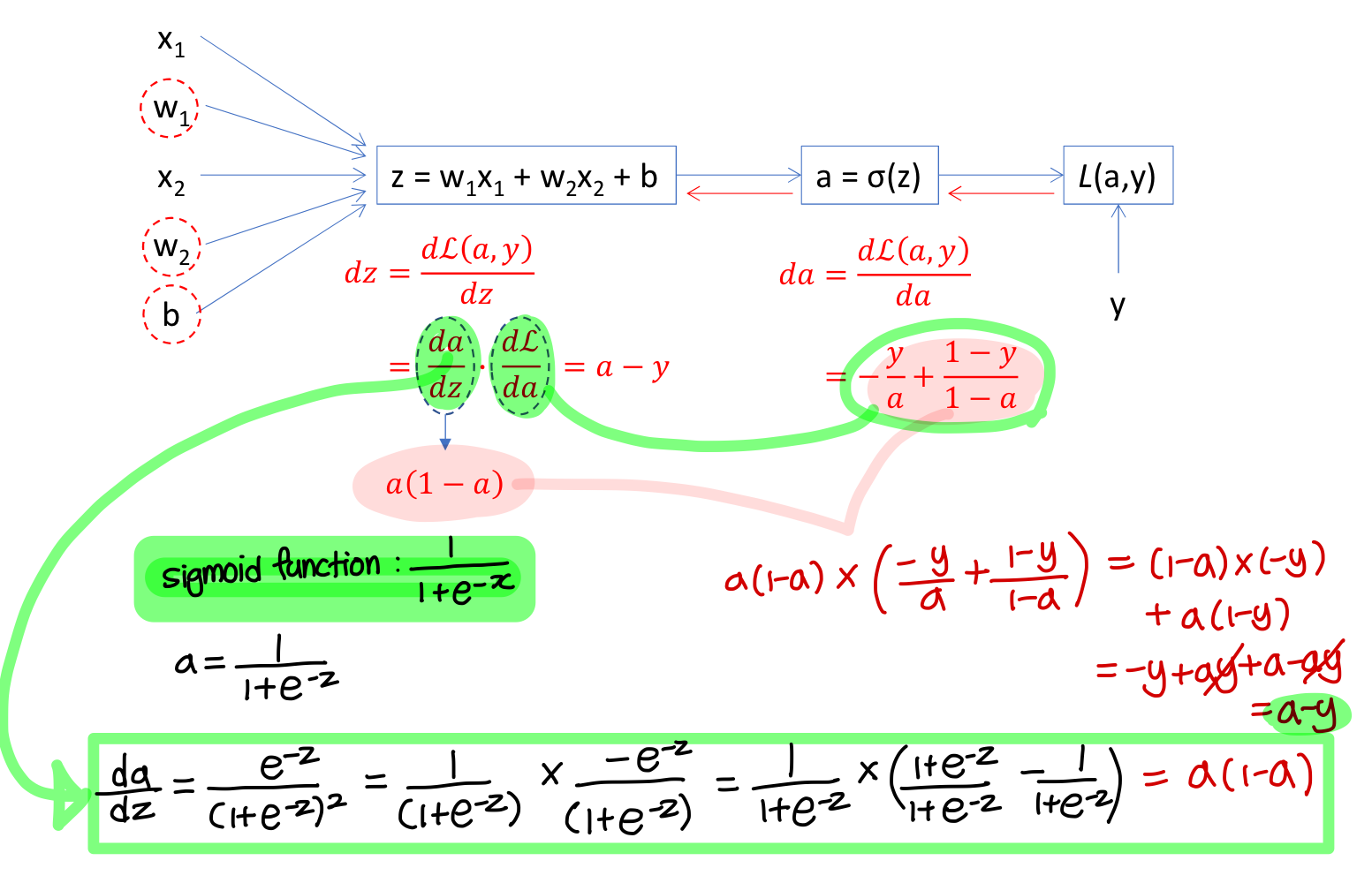
dw_1, dw_2, db 구하기

→ 결론적으로 weight와 bias에 대한 편미분 값은 이렇게 된다.

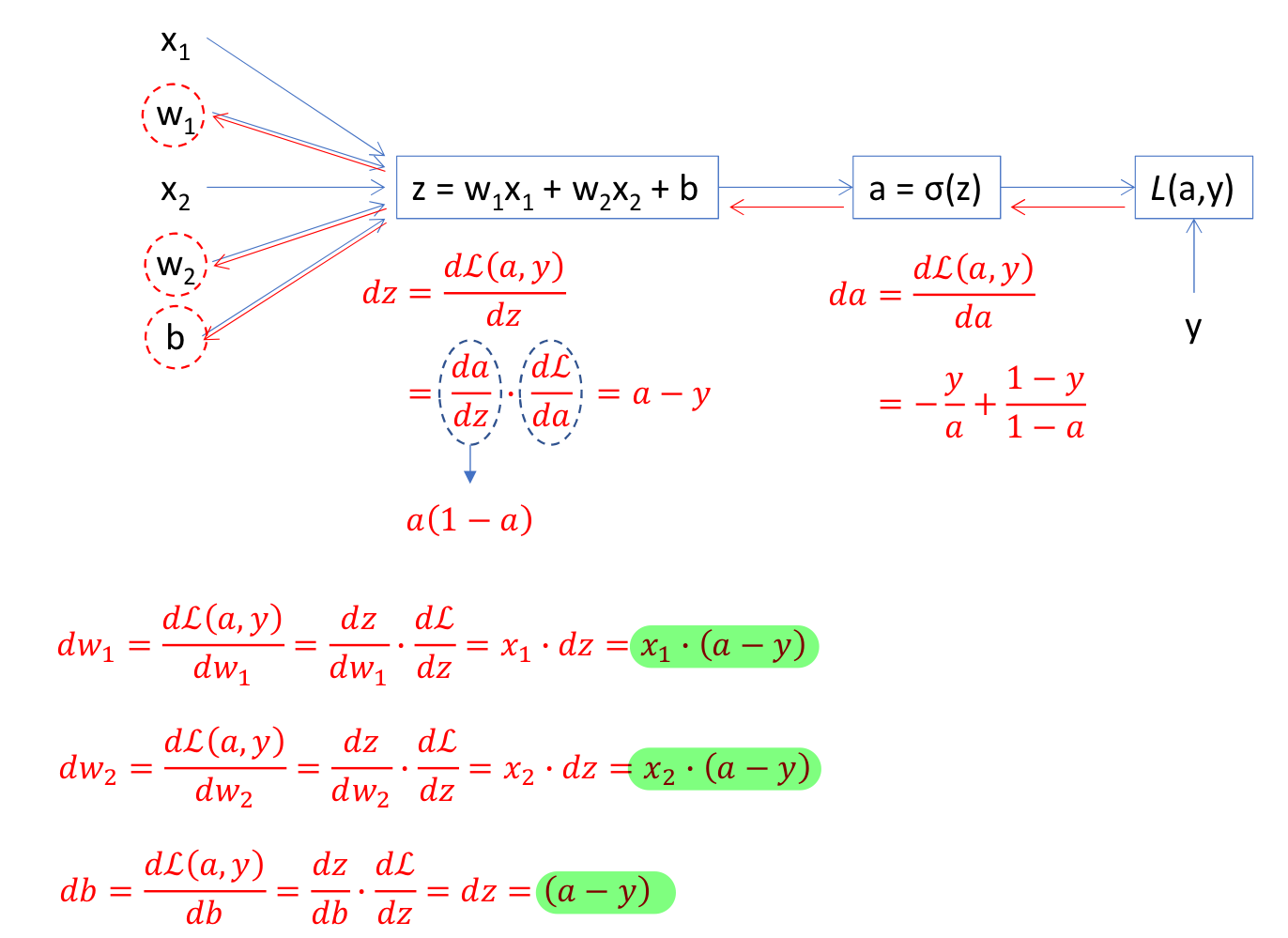
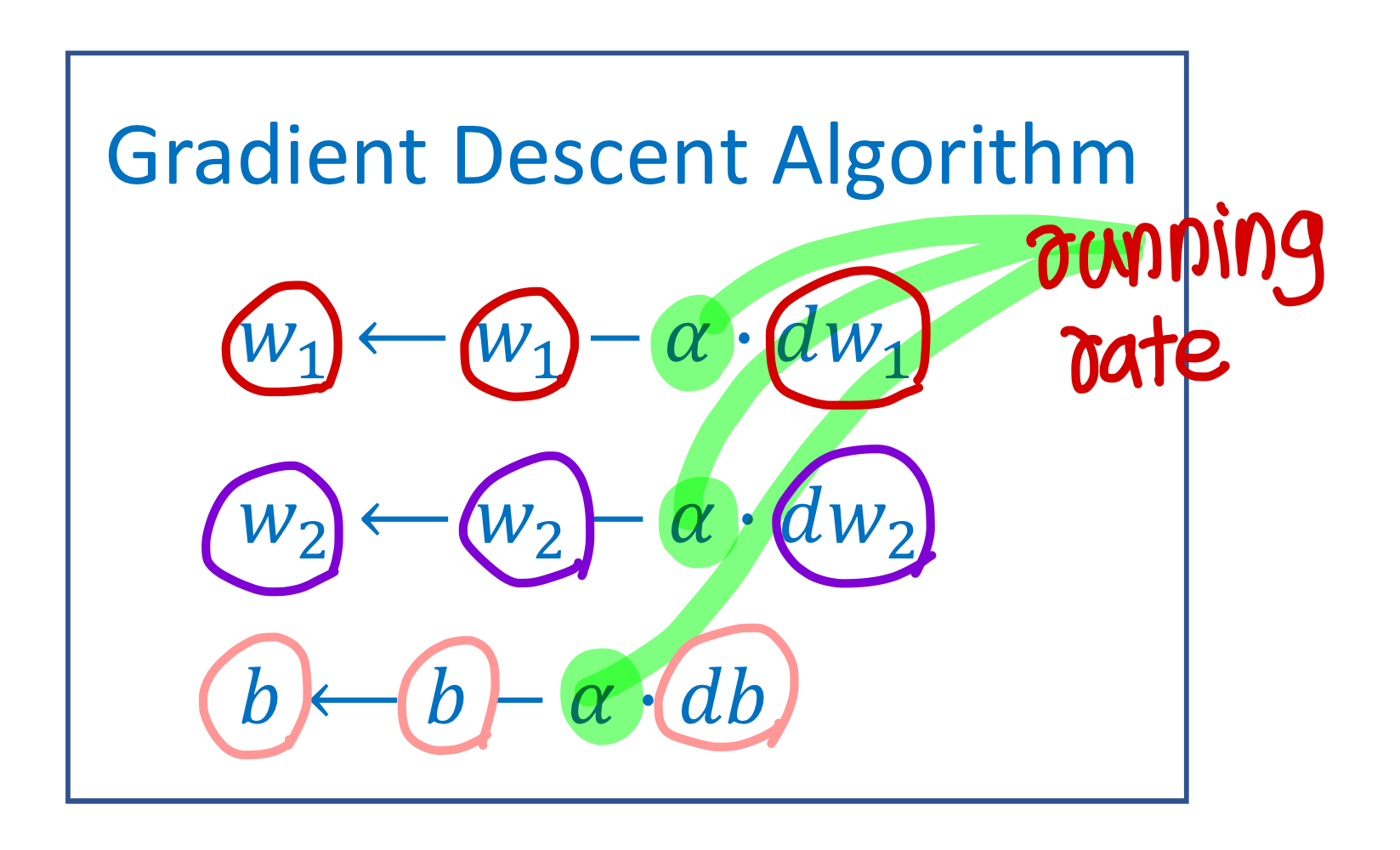
Gradient Descent Algorithm

→ 근데 이건 training data 하나에 대한거임

→ 즉 loss function 하나에 대해 적용한거

---

→ training data 전체에 대해 적용하기 위해선,

즉, cost function에 대해 적용하기기 위해서는

loss function 각각 미분해서 평균내면 됨

Logistic Regression on m Examples

💡

Logistic Regression 이건 뉴런 하나의 모델이라는 점을 기억해라

코드 형식으로 표현하면 이렇게!

1) gradient computation은 이렇게

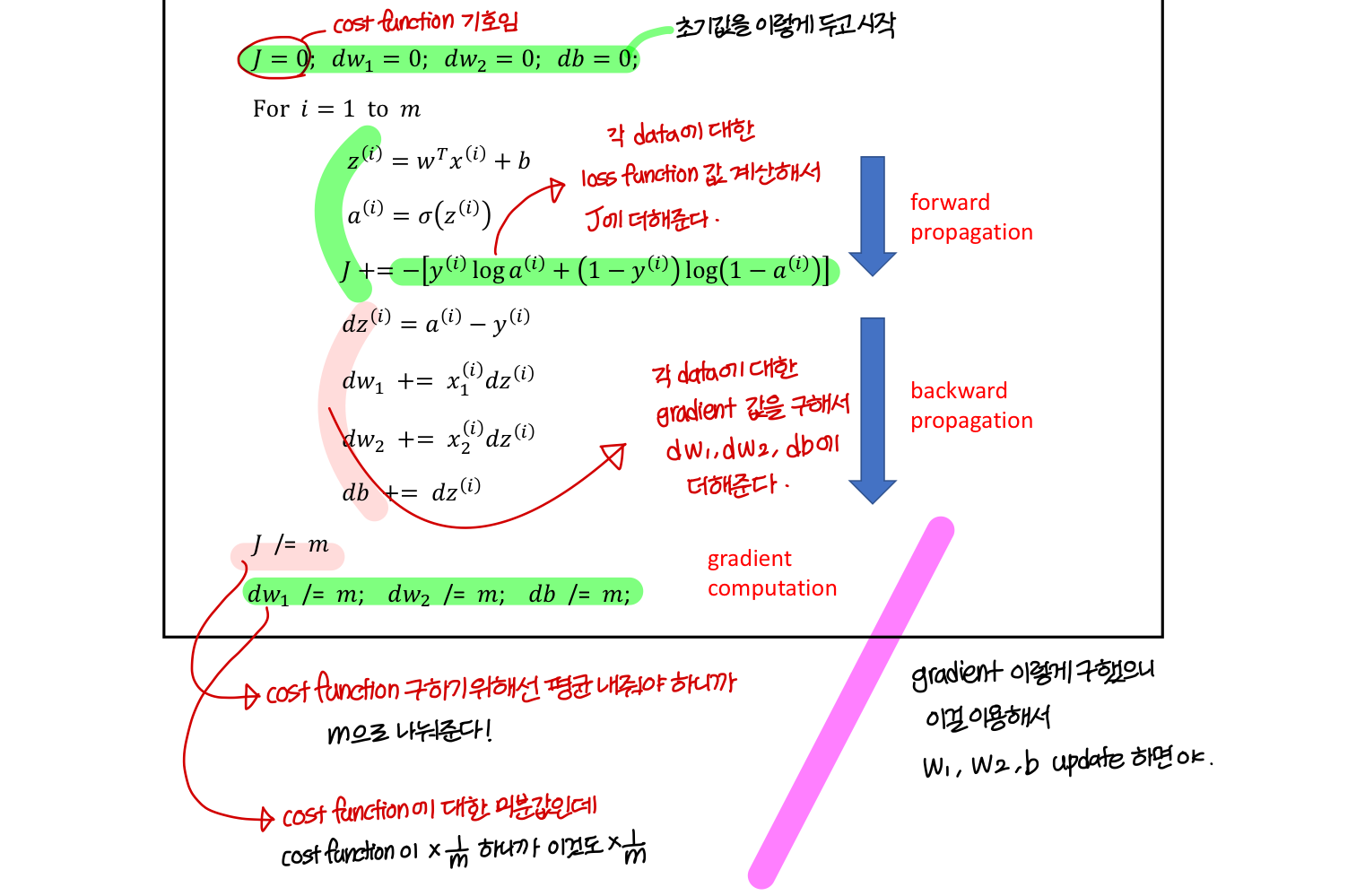
2) parameter update는 이렇게

💡

위의 1) gradient computation, 2) parameter update를 수렵될때까지 반복한다.

Logistic Regression by Gradient Descent Algorithm

Uploaded by N2T