본 논문에서는 motion field라는 structure를 제안하고 있다.
motion field는 어떻게 구성되는지, 또 어떠한 장점이 있는지 차근차근 알아보자.
Preliminary Definition
1. Motion States
character의 state m를 character 모든 joint의 pose와 velocity로 표현하였다. m = (x, v)
(1) pose
x = (x_root, p_0, p_1, ... , p_n)
x_root는 3d root position vector, p_0는 root orientation quaternion, p_1, ..., p_n는 joint orientation quaternion. 즉 root의 position과 root 및 joint의 orientation quaternion으로 pose를 나타내고 있다.
(2) velocity
v = (v_root, q_0, q_1, ..., q_n)
v_root는 3d root displacement vector, q_0는 root displacement quaternion, q_1, ..., q_n는 joint displacement quaternion. 즉 root의 displacement vector와 root 및 joint의 displacement quaternion으로 velocity를 나타내고 있다.
(3) pose와 velocity의 관계
두 개의 pose가 주어졌을 때 difference를 다음과 같이 계산할 수 있다.
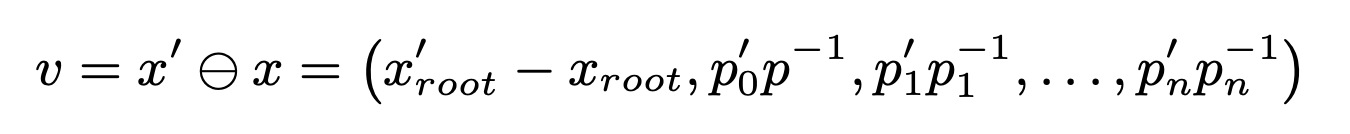
반대로 이런식으로 구한 difference를 pose x에 더해서 x'를 얻을 수 있다.
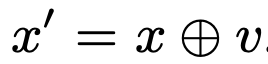
pose들이나 velocities들끼리 lienar interpolation이나 unit quaternion interpolation을 할 수도 있다.
(4) motion state
이런식으로 motion state m = (x, v)를 pose와 associated velocity를 사용해 정의할 수 있다. 이때 v는 x와 바로 다음에 오는 연속된 pose x'를 사용하여 계산한다. (v = x' - x)
2. Motion Database
motion capture data set을 input으로 받아 motion database라고 불리는 motion states의 set을 생성할 수 있다.
motion database의 각 state m_i는 연속적인 frame x_i와 x_i+1로부터 생성되었다.
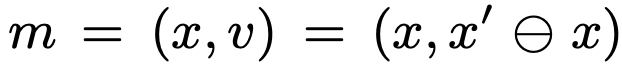
우리는 next pair of frames을 사용해 계산한 velocity까지 계산해서 저장해놓게 된다. (yi = xi+2 ⊖ xi+1.)
3. Similarity and neighborhoods
motion state m이 주어졌을 때 m과 가장 유사한 k-nearest neighbor 를 database로부터 찾게 된다. 이렇게 찾은 k개의 motion state set를 N(m)이라고 부르자. 본 논문에서는 실험을 통해 k=15로 사용하였다.
두 motion state 상의 (dis-)similarity는 다음과 같이 계산한다.
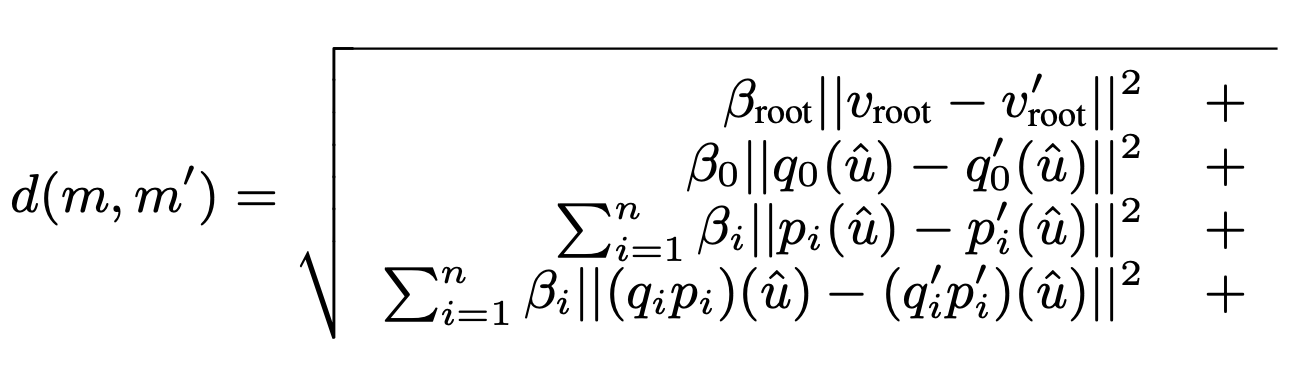
위의 식에서 u hat은 임의의 unit length vector를 의미한다. p(u hat)은 u hat을 p만큼 회전시킨다는 것을 의미한다.
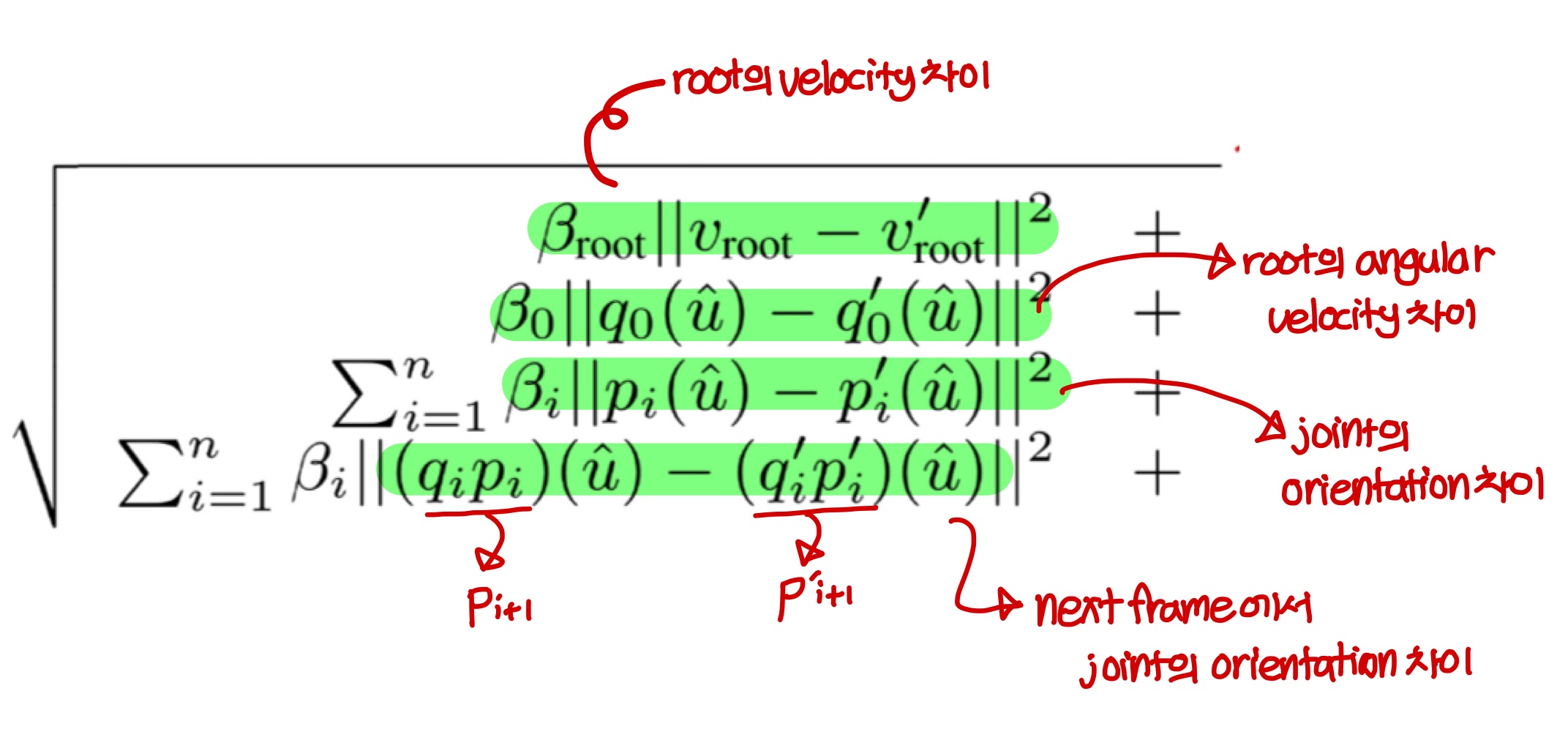
beta_root, beta_0, beta_1..., beta_n은 scalar parameter인데 beta_i 값은 joint i에 위치한 body의 bone length 길이를 meter 값으로 세팅하였다. 그리고 beta_root와 beta_0 의 값은 0.5로 세팅하였다.
직관적으로 설명하자면, joint에 달려있는 bone length가 길수록 motion에 큰 영향을 주고, finger처럼 bone length가 짧은 경우 motion에 큰 영향을 주지 못한다고 판단하여 beta_i의 값은 bone length로 설정하였다.
위의 식을 보면 root의 world position과 orientation은 빠져있다. 대신 respective velcoties는 포함되어있다.
4. Similarity Weight
우리가 database로부터 여러 motion states를 가져오다보니, 우리는 이 N(m)들을 interpolate할 필요가 있다. interpolate할 때 사용하는 weight [w_0, w_1, ..., w_k]를 similarity weights라 부르고, 다음과 같이 계산한다.
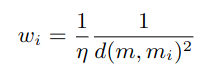
m_i는 N(m)의 i번째 motion state이고
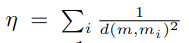
는 weight들의 합을 1로 유지해주는 normalization factor이다.
Motion Synthesis
1. Actions
motion state m일때 motion field A의 value는 control actions의 set A(m)이다. A(m) = [a_1, a_2, a_3, ...a,_k]
그리고 A(m)이 주어졌을 때 next frame m'을 transition 또는 integration function 을 사용해서 결정한다. integration function은 다음과 같다.
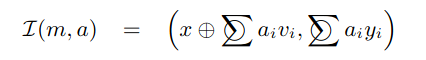
하지만 위의 function을 그대로 사용하면 character's state가 regions를 drift off한다던가 비현실적인 움직임을 만들어낸다던가..등의 문제가 생기게 된다. 이런 문제를 개선하기 위해 motion state m와 가장 유사한 motion state m bar를 database에서 찾아내 character의 움직임이 m bar와 가깝도록 만들어준다. 조금 더 현실적인 움직임이 되도록 보정을 해주었다 생각하면 될 듯하다.
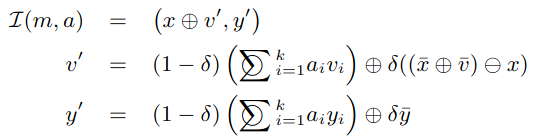
2. Passive Action Selection
이제 우리는 action 값이 정해졌을 때 motion을 어떻게 생성해내는지 알게 되었다. 근데 이 action 값은 어떻게 정해야할까..? 이 내용은 Control part에서 다룰것이다!
일단 가장 simple한 solution은 위에서 다루었던 similarity weight를 사용하는 것이다. action 값으로 similarity weight를 사용할 경우 character는 data를 따라 현실적인 human motion을 만들어낼것이다. (그치만 user input을 반영하지 못하겠지!)
다음 포스트 글에서는 user input을 잘 반영하는 action값을 강화학습을 통해 어떻게 만들어내는지 본겨적으로 살펴보자!
