Intro: Motivation and Curve Representation
Motivation: Why Do We Need Curve?
: Smoothness(no discontinuity)를 표현하기 위해 curve가 필요.
Smmoothness에서는 smooth shape도 있고, smooth movement도 있음.
Curve Representation
- Non parametric (파라미터가 없는 방식)
- Explict: y = f(x)
ex) y = x^2 + 2x - 2
→ 장점: x 값을 넣어주면 대응되는 y 값이 바로 나오니까 point를 표현하기 좋다.
→ 단점: 수직선을 표현할 수 없음. (표현에 제약이 생긴다.)
- Implict: f(x, y) = 0
ex) x^2 + y^2 - 2^2 = 0
→ 장점: 특정 포인트가 곡선 안에 있는지 밖에 있는지 확인하기 쉽다.
→ 단점: point를 생성하기가 불편함.
x 값이 결정되면 바로 y 값이 결정되는게 아니라 추가적인 계산이 필요할 수 있음.
- Explict: y = f(x)
- Parametric: (x, y) = (f(t), g(t))
: 추가적인 파라미터 t를 도입함
ex) (x, y) = (2cos(t), 2sin(t))
→ 장점: 파라미터 t 값이 결정되면 x, y 값이 바로 결정되니까 포인트를 생성하기가 쉽다.
수직선도 자유롭게 표현 가능
→ 파라미터 t가 curve 상에서 local coordinate 처럼 행동한다.
(t에 따라 curve 상에서의 point가 달라진다.)
→ 컴퓨터 그래픽스에서 쓰는 방식은 Parametric 방식!
Polynomial Curve
- Polynomials은 컴퓨터 그래픽스에서 curve를 describe하기 위해 흔히 사용된다.
→ 효율적이고 curve의 모양을 바꾸기도 편하다.
<degree가 n인 polynomial>

Polynomial Interpolation
: smooth curve를 만드는 방법 중 하나는 polynomial interpolation이다.
- interpolation이란: 어떤 포인트들을 주고 그 포인트들을 지나는 함수를 찾는거
- Polynomial interpolation이란: 주어진 data point를 지나는 특정한 smooth polynomial cruve를 결정하는거
1) Linear interpolation은 degree가 1인 polynomial 로 한 interpolation
→ input: two nodes;
→ output: Linear polynomial

2) Quadratic interpolation은 degree가 2인 polynomial로 한 interpolation
→ 이땐 찾아야 하는 값이 3개니까 점이 3개 필요
3) Polynomial interpolation of degree n
Problem of Higher Degree Polynomial Interpolation
: 많은 점이 주어지면 정보가 더 많이 주어져서 좋을 것 같지만 사실은 문제가 있다.
→ 차수가 높아지면 양쪽 끝부분에서 진동이 커진다. 이 현상을 Runge's Phenomenon 이라고 부름

: 이런 문제 때문에 아무도 higer degree polynomial interpolation을 사용하지 않는다.
Cubic Polynomials
: 너무 고차원이면 Runge's Phenomenon이 생기니까 컴퓨터 그래픽스에선 Cubic(degree of 3) polynomials을 사용한다.
→ 2차 polynomials은 점이 3개가 주어지는데 3차원에서 점 3개는 항상 같은 평면 상에 존재한다.
→ 평면에서 벗어나는 곡선을 그리려면 2차보다 높아야함.
→ 3차 정도면 양끝이 튀는 현상도 없고, 평면에서 벗어나는 곡선도 그릴 수 있다.

Then, how can make complex curves using such a low degree polynomial?
: Cubic(3차) polynomial을 가지고 어떻게 복잡한 곡선을 표현할까?
→ Answer: Spline을 사용하기
curve를 여러개를 연결해서 복잡한 모양을 만들 수 있다. 연결을 잘하면 부드럽게 연결이 가능하다.
→ 수업땐 spline에 대해 자세히 다루진 않을거고, 그냥 single piece of polynomial이라고 생각을 하자.
Defining a Single Piece of Cubic Polynomial

- Goal: 우리가 지정한 data point를 지나는 specific curve를 Define 하는거. (즉, a, b, c, d를 결정하는거)
- 4개의 벡터 unknowns이 있으므로 4개의 equation이 필요.
→ 1) 점 4개를 줄수도 있고
→ 2) 점 2개와 그 점 2개에서의 derivative(변화율)을 줄수도 있다.
Formulation of a Single Piece of Polynomial
<polynomial은 2가지 방법으로 표현 가능>
1) coefficient와 variable로 표현하는 방법
2) basis function이랑 points로 표현하는 방법
Meaning of Basis Function
(이부분 다시)
Quiz #1

x(t) = (1-t)* p_0 + t * p_1
= (1-t) * 1 + t * (-2) = 1-t-2t = 1-3t
답) x(t) = -3t+1
Hermite curve
Hermite curve
- cubic polynomial들을 연결해서 curve를 표현한다.
- condition 4개가 필요한데, 양 끝점과 양 끝점에서의 변화율(기울기)로 준다. (양끝점일때 t = 0, t = 1로 보는게 편함)
즉, 위에서 구한 a, b, c, d를 사용해 식을 정리하면

Coefficients = rows
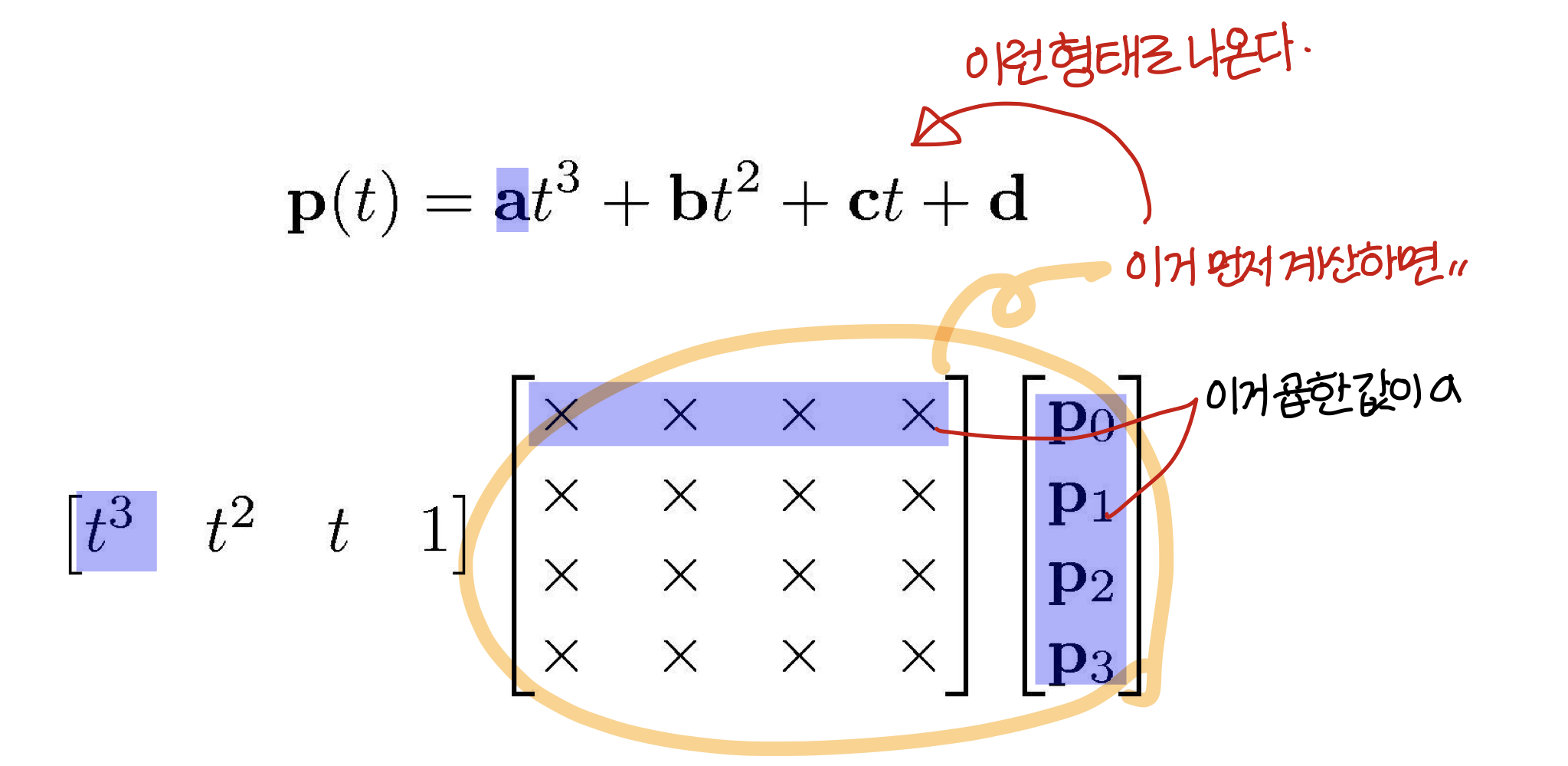
Basis functions = columns
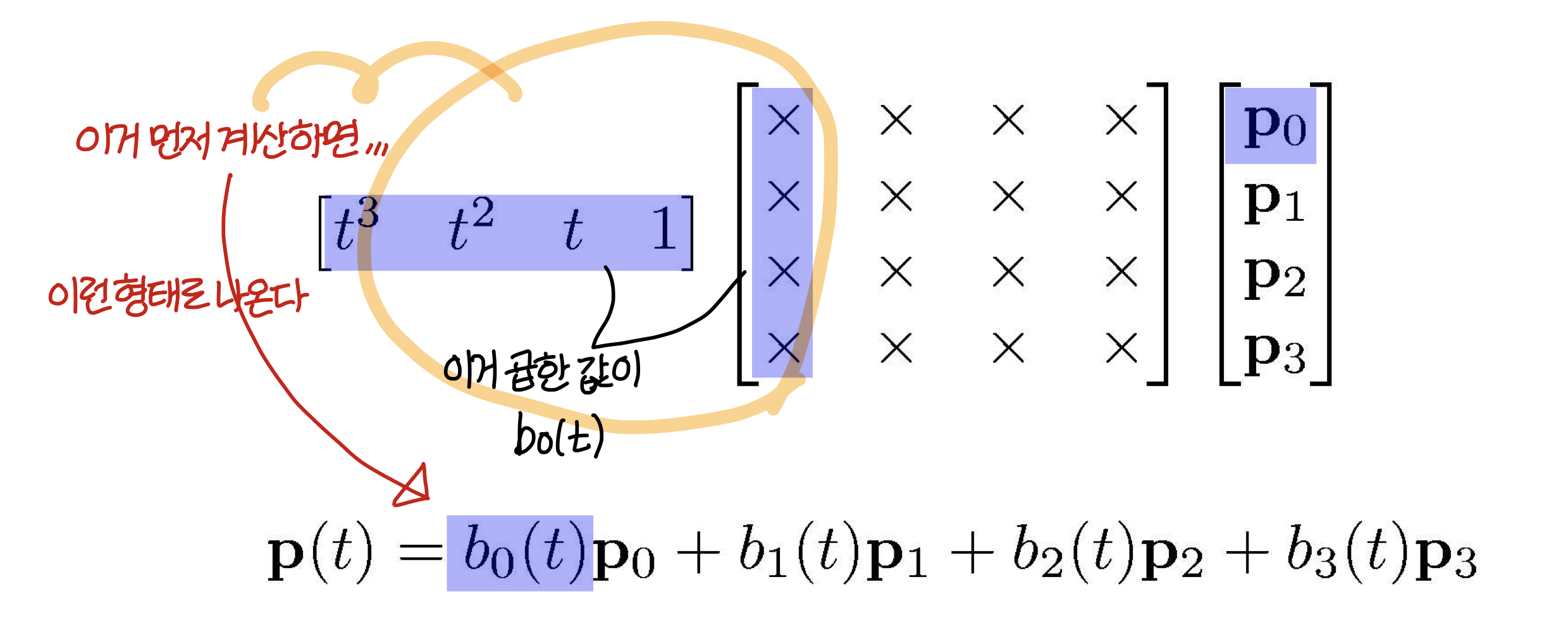
→ 위에꺼랑 같은 식인데 무슨 단위로 생각하느냐에 따라 위에 식으로도 볼 수 있고 아래식으로도 볼 수 있음.
Hermite basis functions

[Practice] Hermite Curve Online Demo

Quiz #2

Bezier Curve
Hermite to Bezier
- Hermite에서는 condition을 벡터 2개와 포인트 2개로 줬음.
→ 이렇게 벡터랑 포인트가 섞여서 주어지는게 이상하다고 생각해서 4개의 점으로 condition을 줄 수 없나 해서 나온게 Bezier
- Bezier에서는 다음과 같이 condition을 제시한다.

- 베지어 커브가 허밋커브로 어떻게 변환되는지 생각하면 Bezier matrix를 쉽게 구할 수 있다.

→ 이걸 a, b, c, d 구하는 식에 대입하면
→ 정리하면

→ 여기서 중요한게, 베지어 커브에서 각 control point에 곱해진 basis function은 사실,
Bernstein polynomials이라고 불리는 polynomoal이다.
→ Berstein polynomial이란 다음과 같이 표현되는 polynomial

→ Bezier Curve에서 사용되는 Bernstein basis function을 구해보면

→ 즉, Bezier Curve를 정리하면 이렇게 된다

Bezier basis
de Casteljau's Algorithm
: 베지어 커브를 계산하기 위한 Another method
→ 사실 이게 먼저임. 먼저 알고리즘을 만들었지만 publish를 못해서 다른 이름이 붙여진거
<방법 → 3단계의 linear interpolation이 필요하다>


<이렇게 나오는 이유 → 식으로 풀어보면 당연한거임>

<de Casteljau's Algorithm의 특징>
- de Casteljau's 알고리즘은 베지어 커브 위의 point를 계산하는 좋은 "recursive algorithm"이다!
→ 베지어 커브를 2개의 베지어 커브 segment로 나눌 수 있다. 이걸 subdivision 이라고 한다!

- "Subdivision" method는 굉장히 유용하다. → 특정한 부분만 끊어서 editing 하는게 가능
- 그리고 "Subdivision"을 많이 하면 작은 segment의 control point를 잇는것만으로 approximate한 베지어 커브를 만들 수 있음
→ 하드웨어에서 곡선을 그리는걸 지원하지 않음.
→ 결국 컴퓨터그래픽스에서는, 작은 line들이 모여서 approximate한 curve를 만들도록 해야하는데
이때 de Casteljau's 알고리즘 자체가 랜더링 방식이 될 수 있음.
→ (영어표현) You can draw a curve with a sufficient number of subdibided control points.
"Subdibision" method for displaying curve
Displaying Curves
Curve를 실제로 어떻게 랜더링하는지와 관련된 이야기
- 위에서도 말했듯이, line segment를 여러개 잇는 식으로 approximate한 curve를 그려야한다.
(curve를 그리는걸 지원하는 하드웨어는 없으므로)
<Curve를 렌더링하는 3가지 방법>
1) Brute-force
: t 값에 따른 p(t)를 계산하면 점들이 나오는데 그 점들을 잇는게 brute-force 방식
→ 근데 이렇게 하면 중복된 계산이 계속 생긴다.
2) Finite difference
: Brute-force와 같은 방식인데 중복된 계산을 줄인 방법
3) Subdivision
: (앞에서 언급한 방법) Casteljau's algorithm을 이용해 subdivision을 많이 해서 나오는 control point를 잇는 방법
Properties of Bezier Curve
- control point 4개로 곡선을 직관적으로 control 할 수 있다.
- curve가 항상 contorl points의 convex hall 안에 있다.
Convex hall: 주어진 포인트들을 모두 포함하는(꼭짓점으로 쓰든, 내부에 넣든) 가장 작은 볼록 다각형

- 양끝점을 지나는 curve를 만든다.
→ 이 말을 "End point interpolation"이라고 표현함..
Quiz #3

Bezier Spline
- piecewise Bezier curves의 combination인, Bezier spline이 실제로 엄청 많이 사용된다.
- Adobe Illustrator과 같은 그래픽 툴에서 shapes를 그리는데도 사용되고,
- 블렌더나 마야와 같이 3D authoring tools에서 animation paths를 define하는데도 많이 사용된다
- TrueType font 같은 경우는 quadratic Bezier spline (2차 다항식 사용) 을 사용하고
PostScript font 같은 경우는 cubic Bezier spline (3차 다항식 사용, 우리가 배운거)을 사용한다.
→ 이렇게 curve를 사용해 폰트를 나타내면 폰트를 확대해도 깨지지 않고 매끄럽게 나타난다.

→ 이어지는 곳의 tangent가 같아지게 하면 된다.

Spline
- Spline: piecewise polynomial
- Spline과 관련된 3가지 이슈
1) pieces들을 continuously 하게 어떻게 잇나?
2) spline의 shape를 어떻게 쉽게 control할 수 있나?
(local하게 조절할 수 있을 수록 control이 쉬운거임)
3) spline이 주어진 point를 정확하게 지나야하는지, 아니면 주변으로 가는 경향만 있으면 되는지
→ 이 조건에 따라 사용하는 spline type도 달라진다.
Uploaded by N2T















