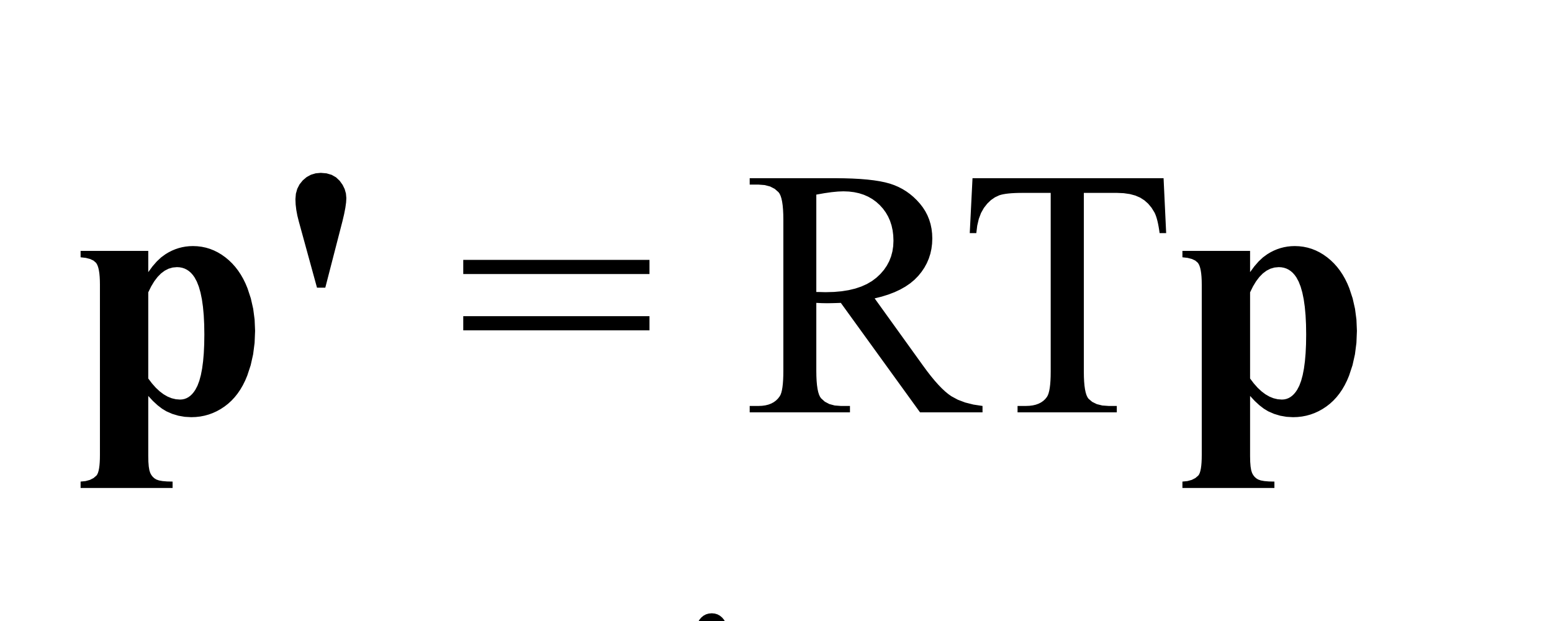Meaning of an Affine Transformation Matrix
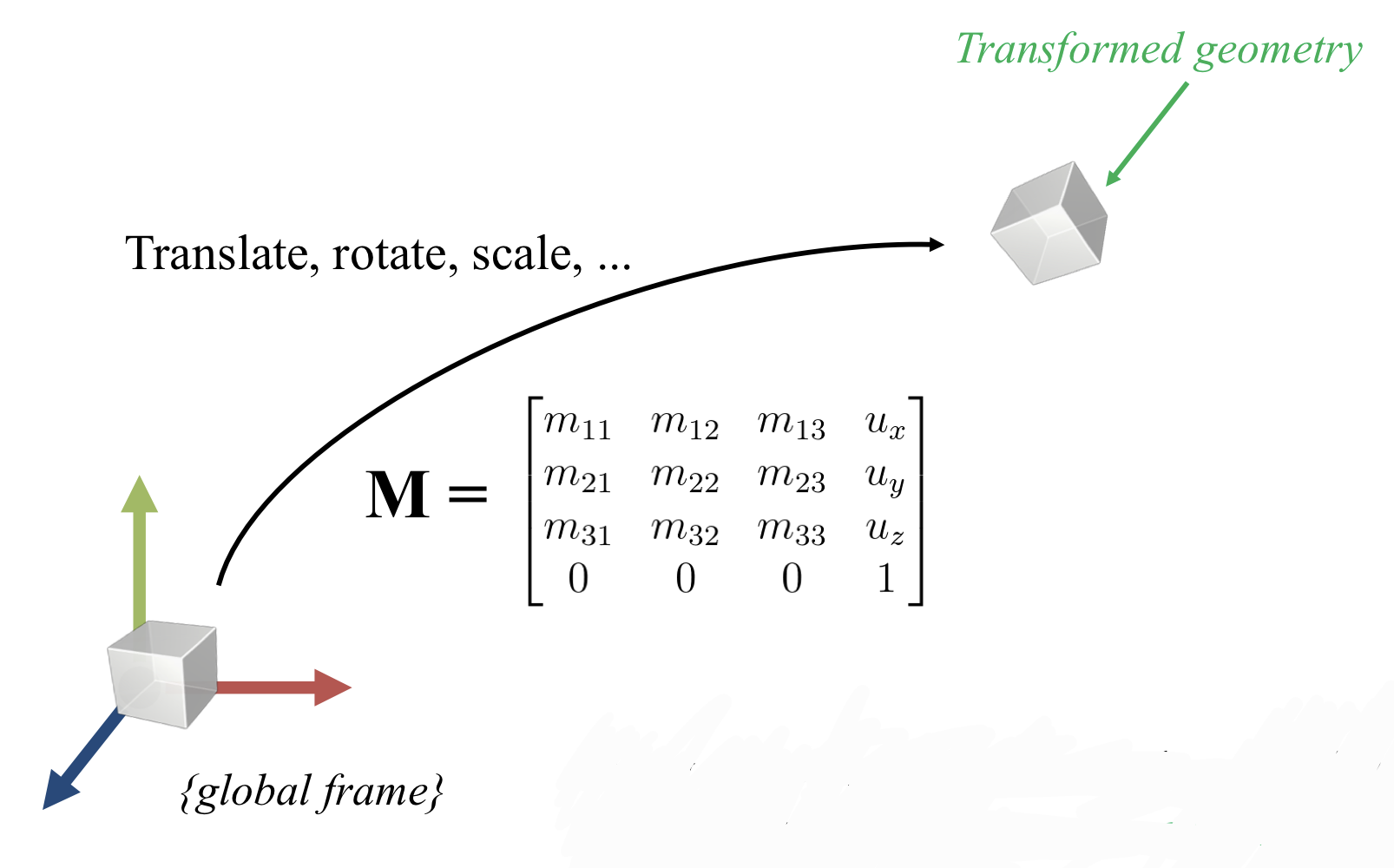
1) A 4X4 Affine Transformation Matirx transforms a Geometry w.r.t. Global Frame
→ 우리에게 가장 익숙한 의미
→ (global frame에 대해 기술된) 모든 vertex가 (global frame에 대해 기술된) 다른 position으로 transformed 되는거
Review: Affine Frame
3D space 상에서의 affine frame은 3개의 vectors와 하나의 point로 일워짐
→ x, y, z 축을 의미하는 3개의 vector와
→ 원점을 의미하는 하나의 point
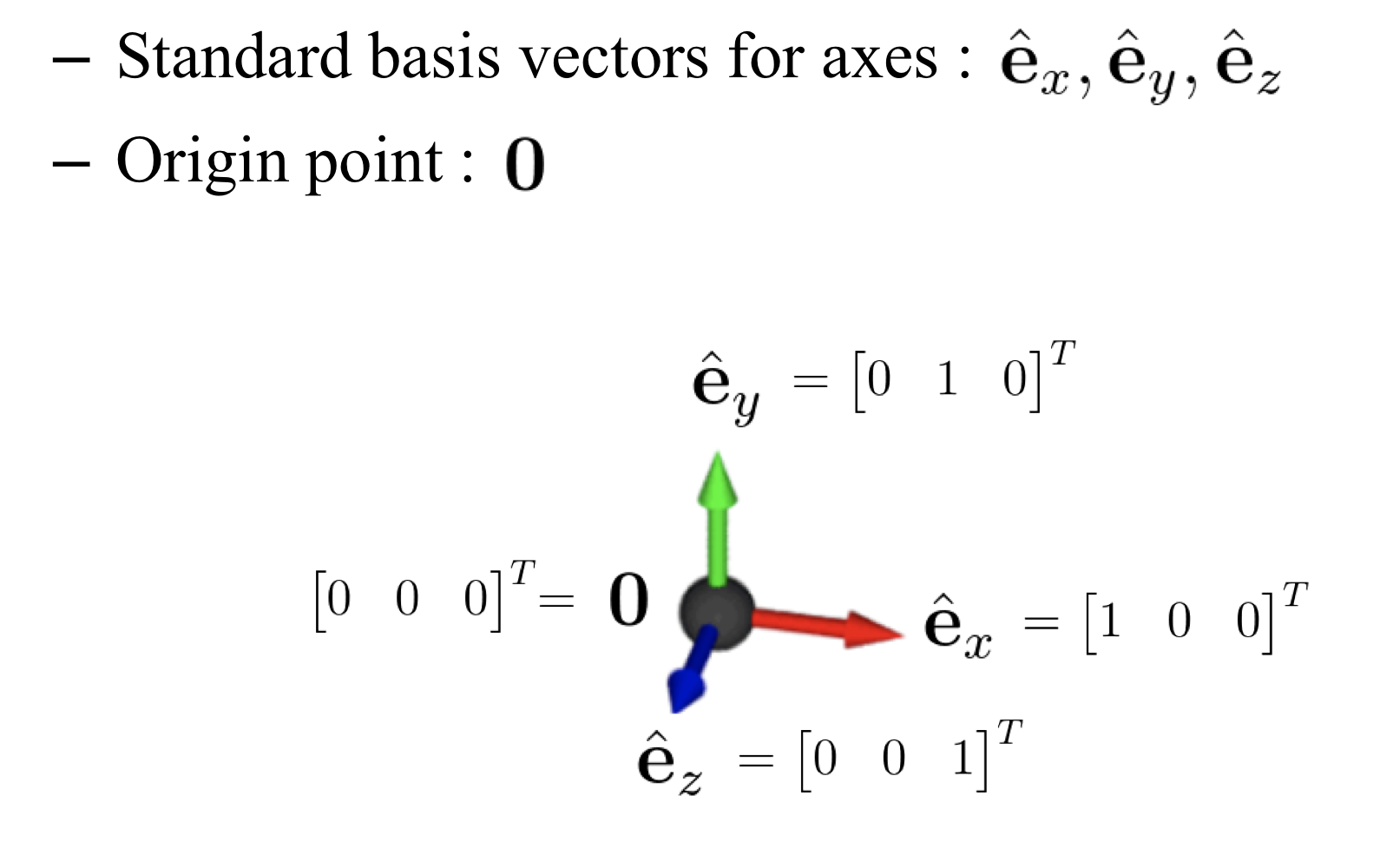
Global Frame
global frame은 다음과 같이 표현된다.
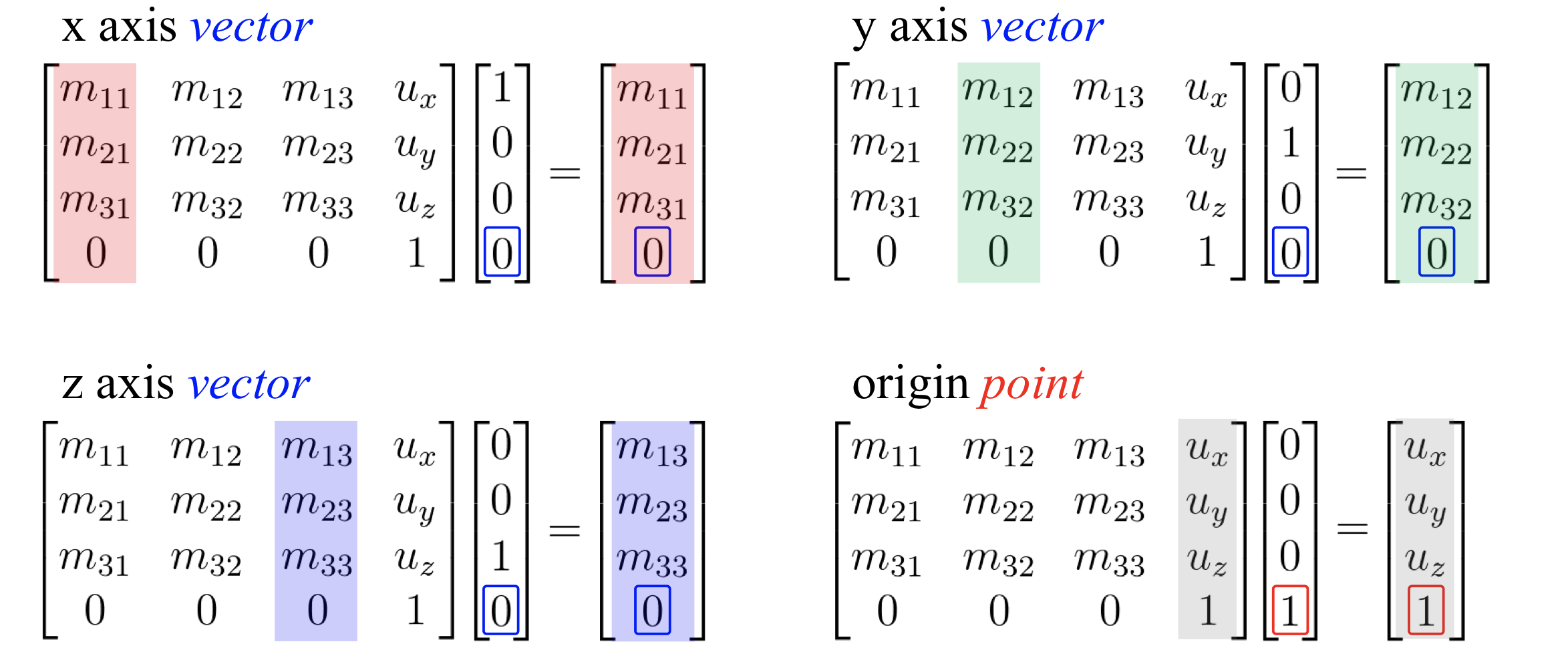
Let's transform a "global frame"
global frame에 M을 곱하면(vectors for axes과 origin point) 어떻게 변하는지 보자.
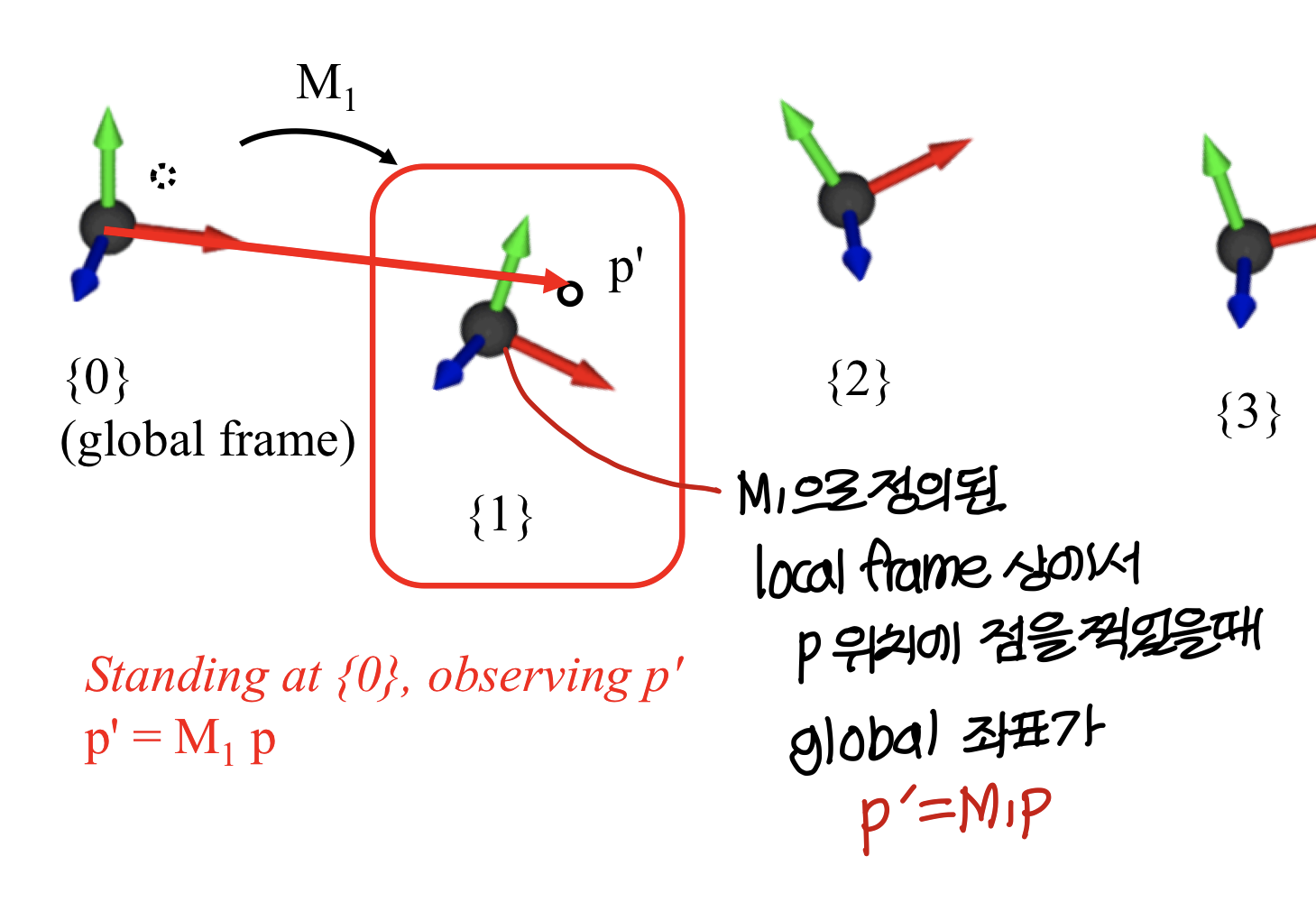
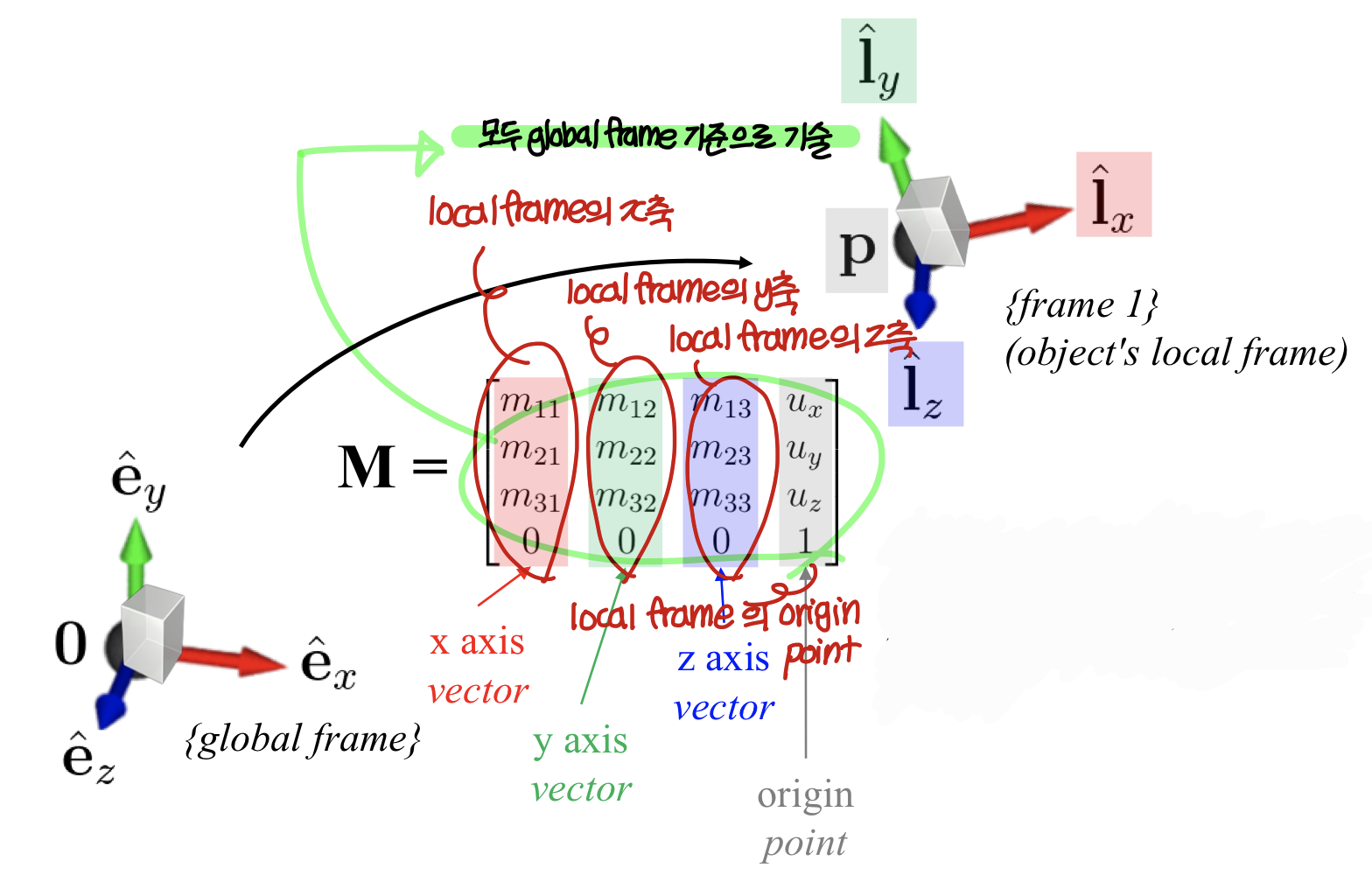
2) A 4X4 Affine Transformation Matrix defines an Affine Frame w.r.t. Global Frame
→ global frame 상에서 새로운 local frame을 정의한다고 보면 된다.
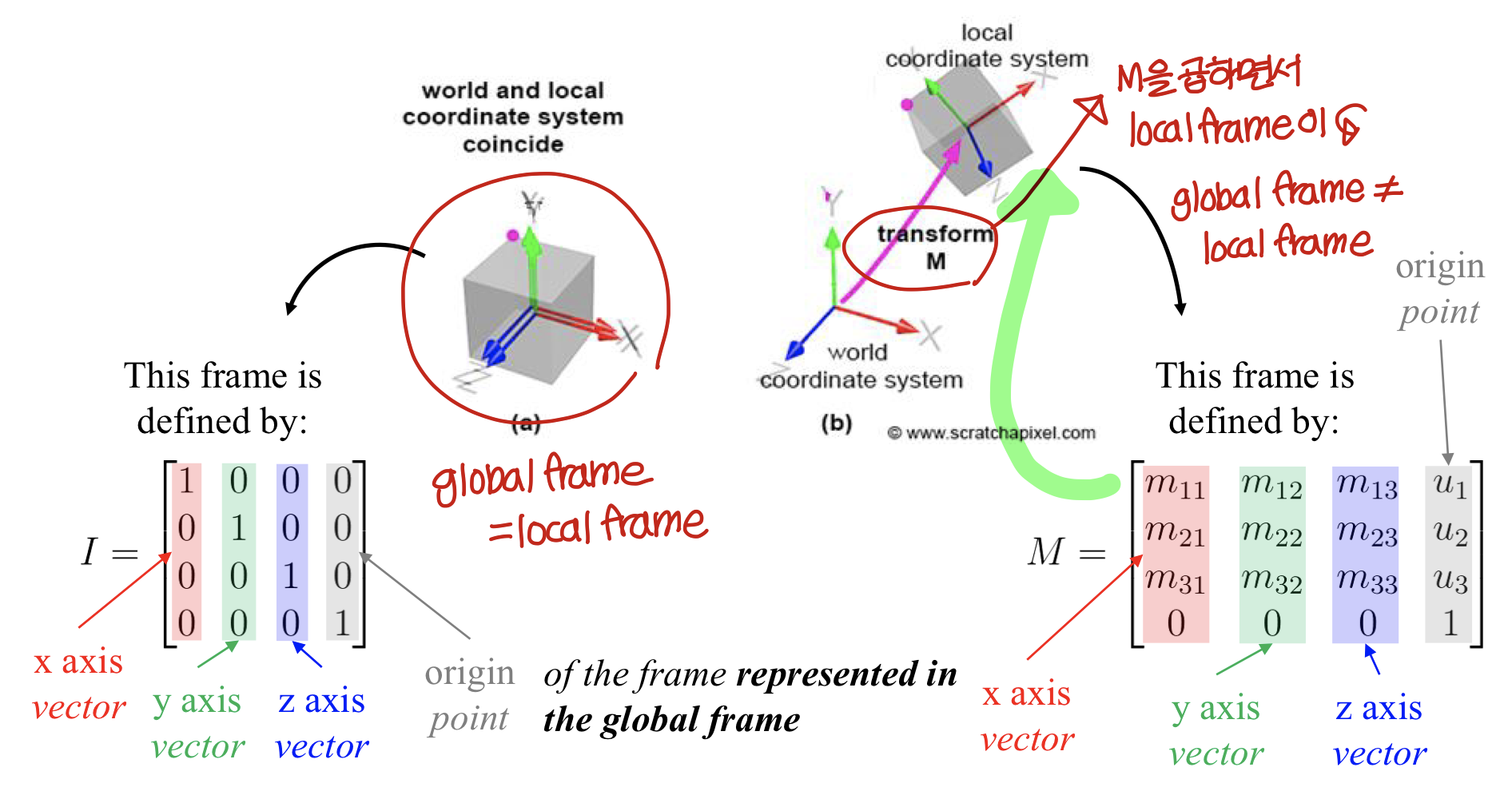
Example
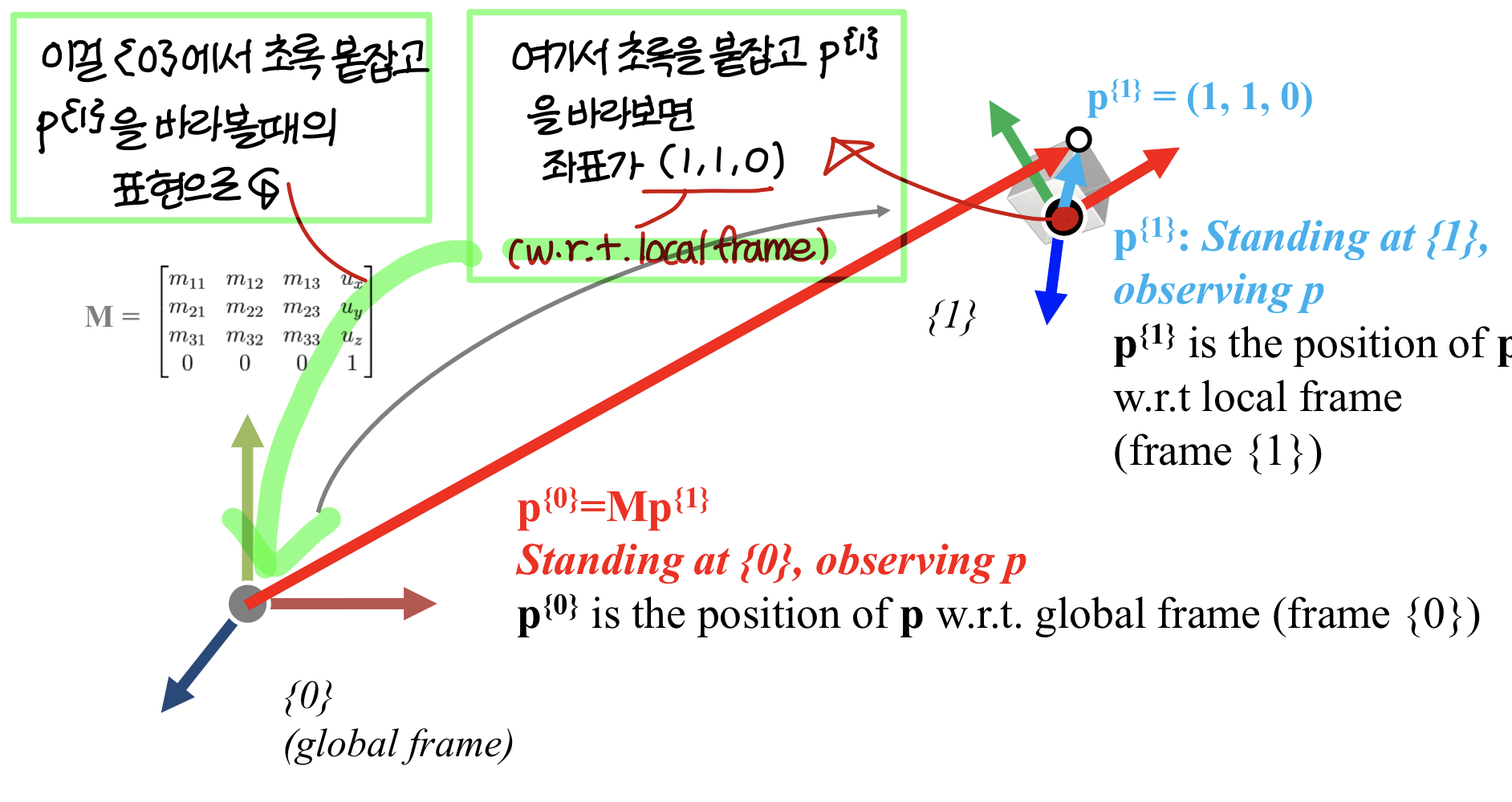
3) A 4X4 Affine Transformation Matrix transforms a Point Represented in an Affine Frame to (the same) Point (but) Represented in Global Frame
→ local frame 상의 점을 global frame 상의 수치로 표현 가능하게 해줌
Quiz #1

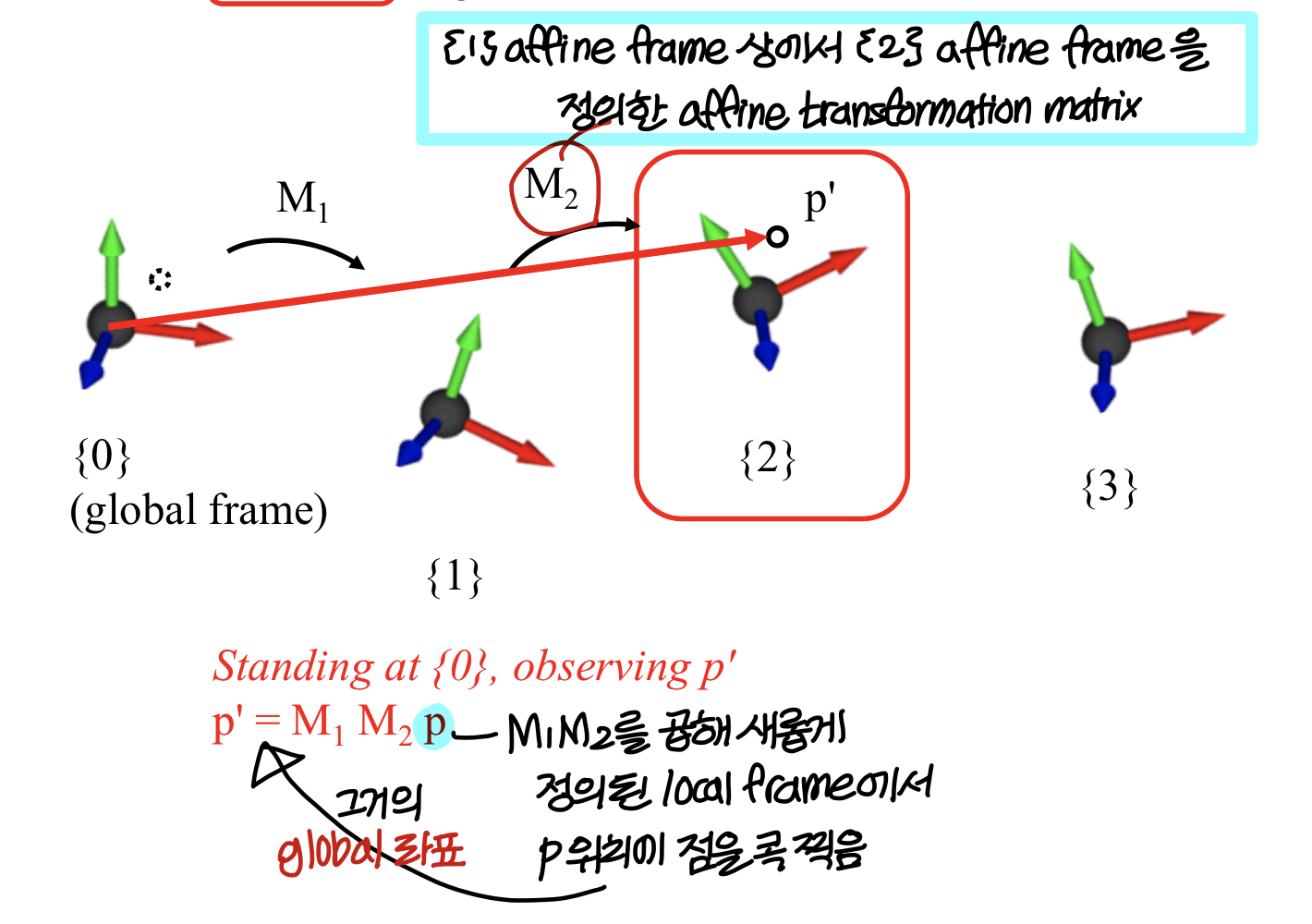
All these concepts works enven if the original frame is not glboal frame
→ 우리 global frame에 대해 설명했지만, 시작 frame이 global frame이 아니라도 이 개념이 똑같이 적용된다.
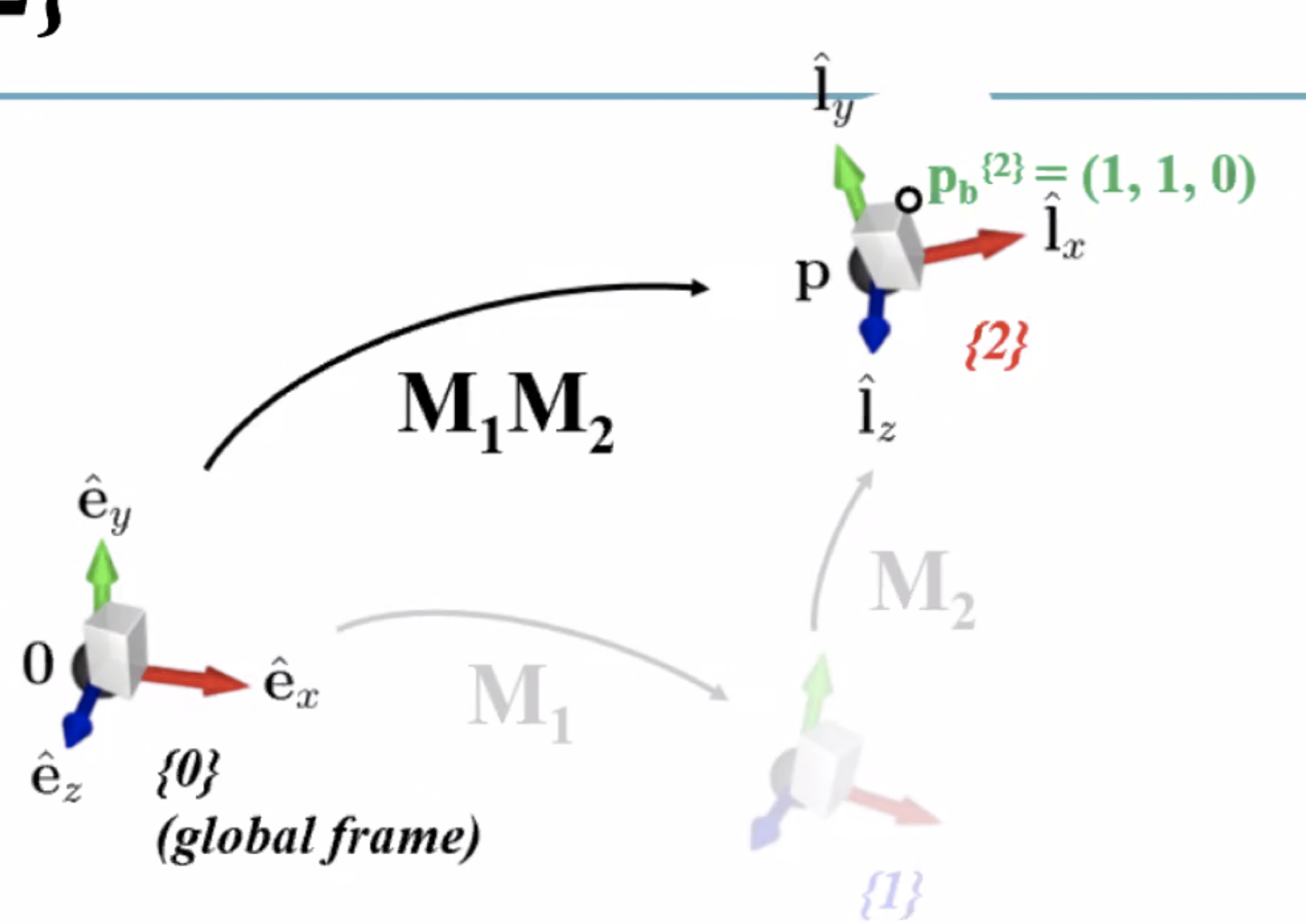
→ 이걸 앞에서 배운 3가지의 의미로 해석할 수 있다.
1) M_1 M_2 를 곱해서 geometry를 transform한다. (global frame 상에서 표현된 점을 global frame 상의 다른 위치로 이동시킴)
2) M_1 M_2는 {2} frame을 정의한다. (w.r.t. {0})
3) M_1 M_2는 {2}상에서 표현된 점을 {0}상에서의 표현으로 바꾼다.
→ 그건 global frame에 대한 변환이고 이건 local frame에 대한 변환이라 조금 경우가 다르다.
→ M_2를 곱하는 걸 뜯어서 살펴보면...
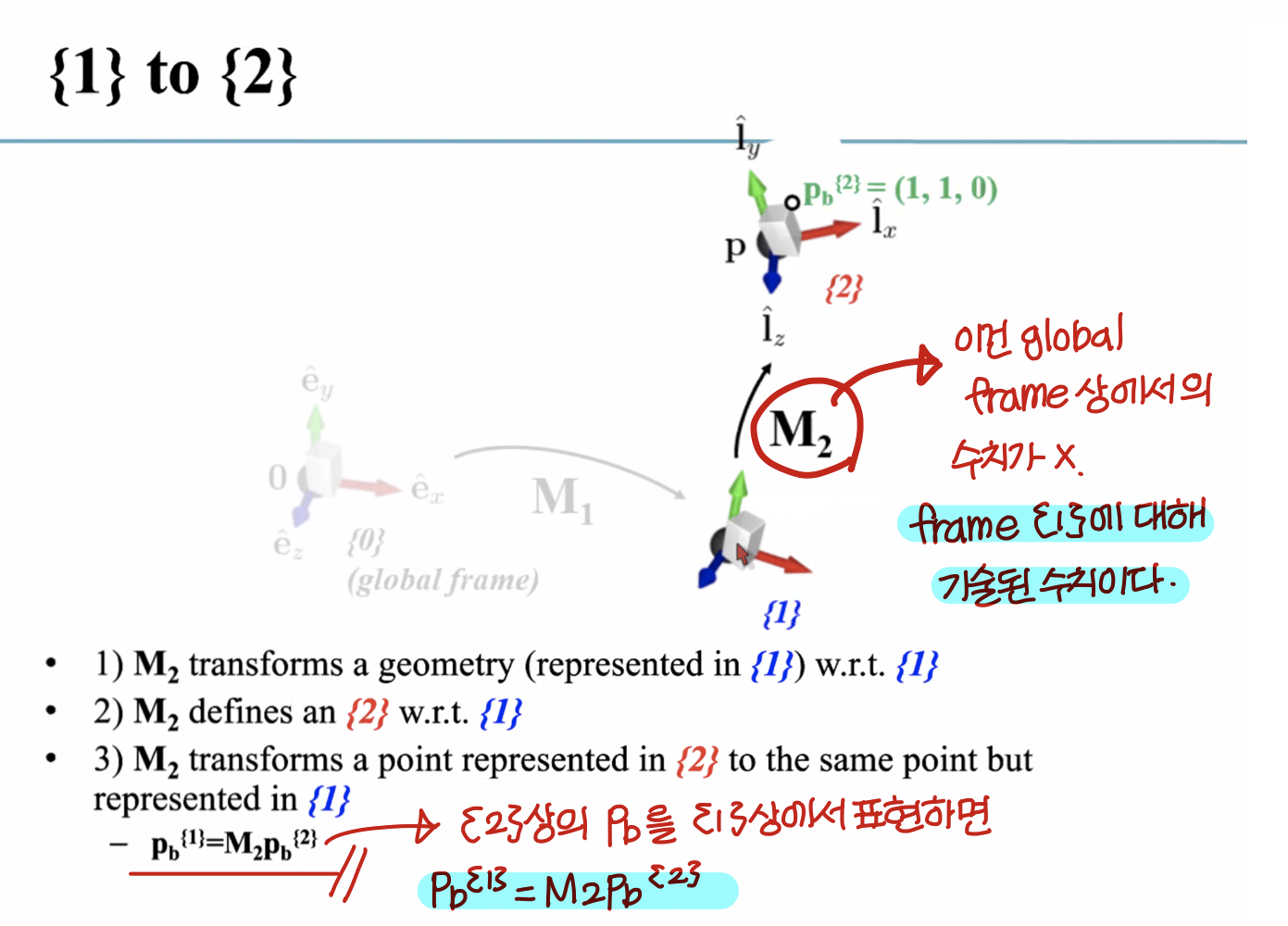
→ 만약 M_2가 globalframe에 대해 기술된거고 M_1→M_2를 적용하고 싶은 거라면 M_2 M_1를 곱해야겠지만
→ 지금의 M_2는 local frame에 대해 기술된거 그래서 M_1 M_2를 곱해야한다.
→ 근데 예외적으로 3번째 해석같은 경우엔 M2 → M1 순으로 적용한다고 해석해서 M_1 M_2를 곱함
(물론 곱하는 matrix가 global frame에 대해 기술된건 아니고 local 에 대해 기술된거긴 함)
Interpretation of a Series of Transformations
Revisit: Order Matters!
- T와 R은 affine transformation을 의미한다.
Interpretation of Composite Transformations #1
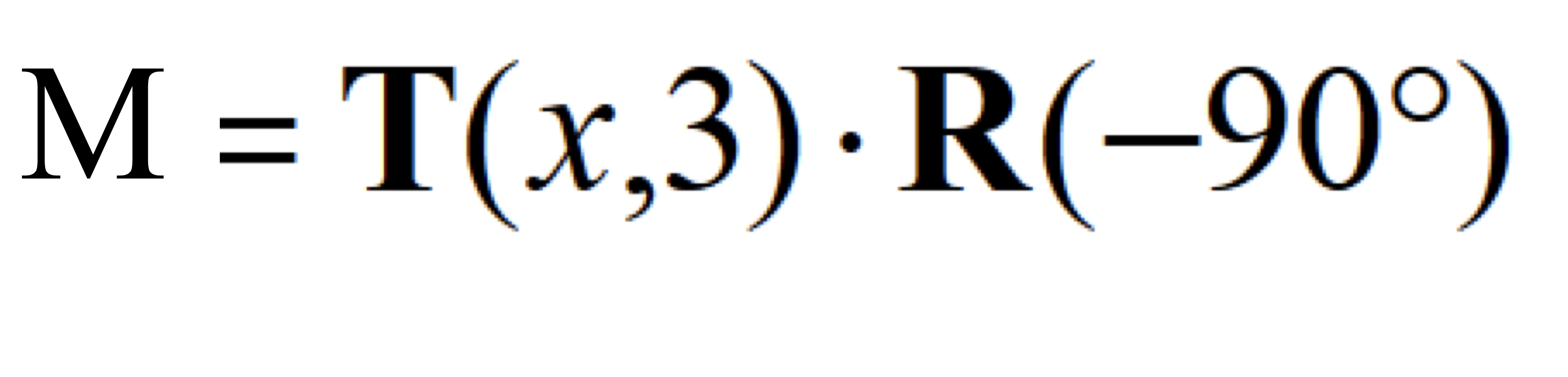
R→T로 해석하려면 R도 global frame에 대해 기술된거고, T도 global frame에 대해 기술된거로 봐야한다.
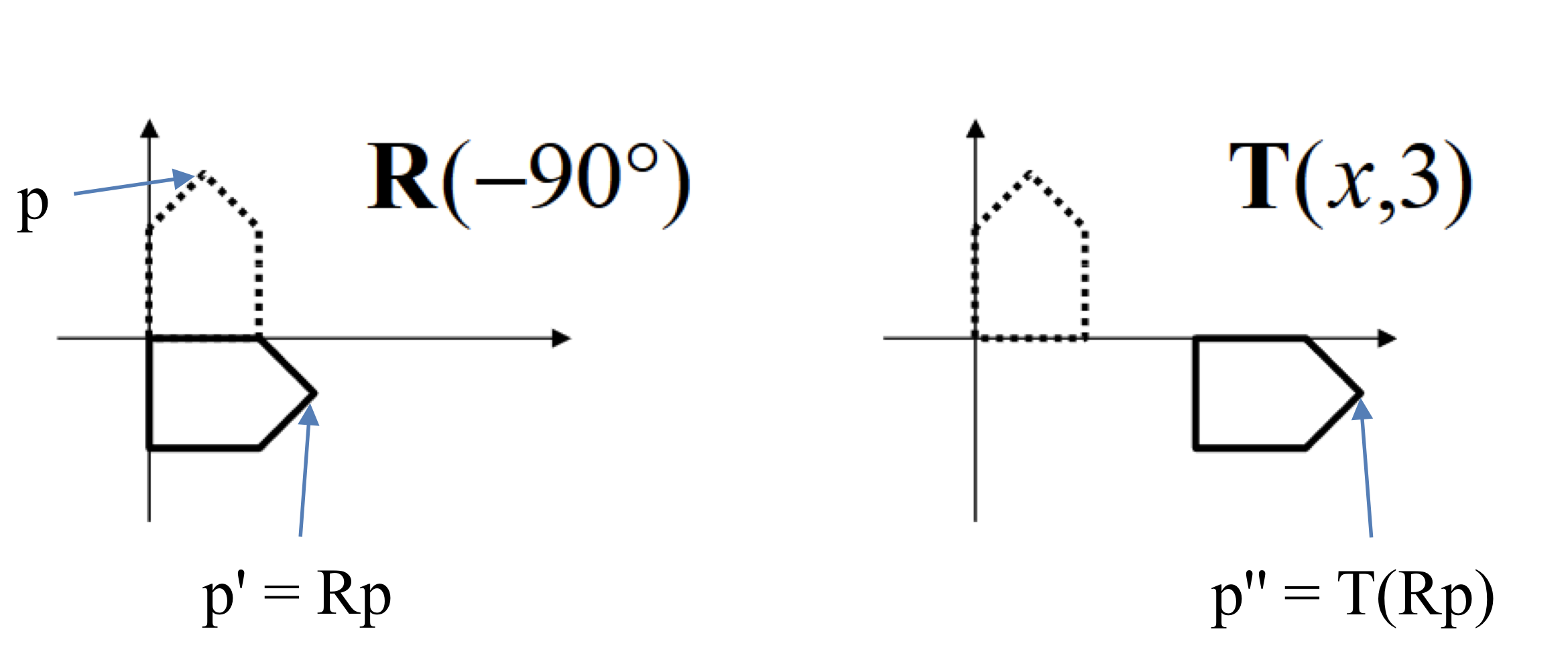
Interpreation of Composite Transformation #2
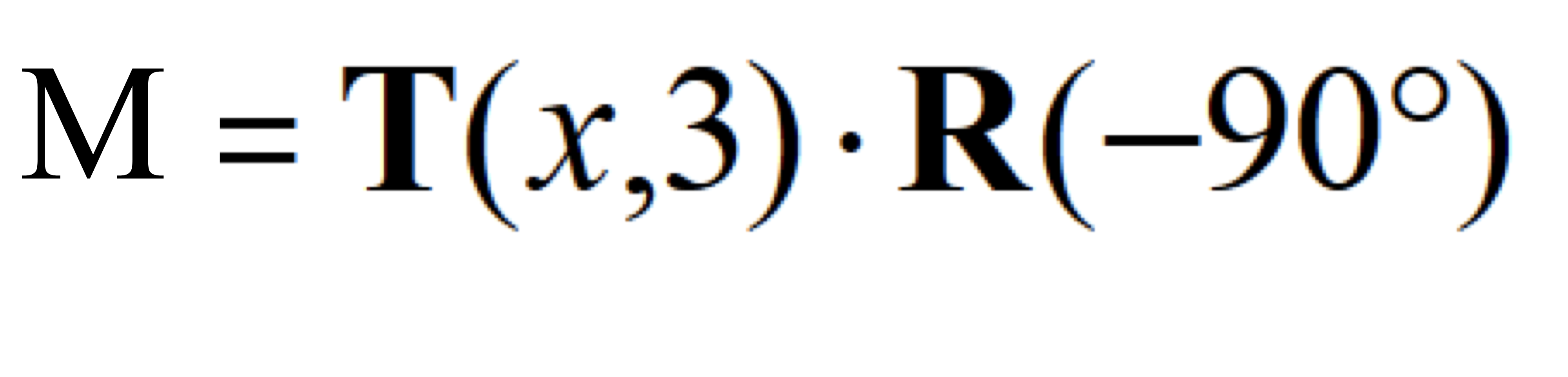
T→R로 해석하려면 local frame에 대해 적용된다고 봐야한다.
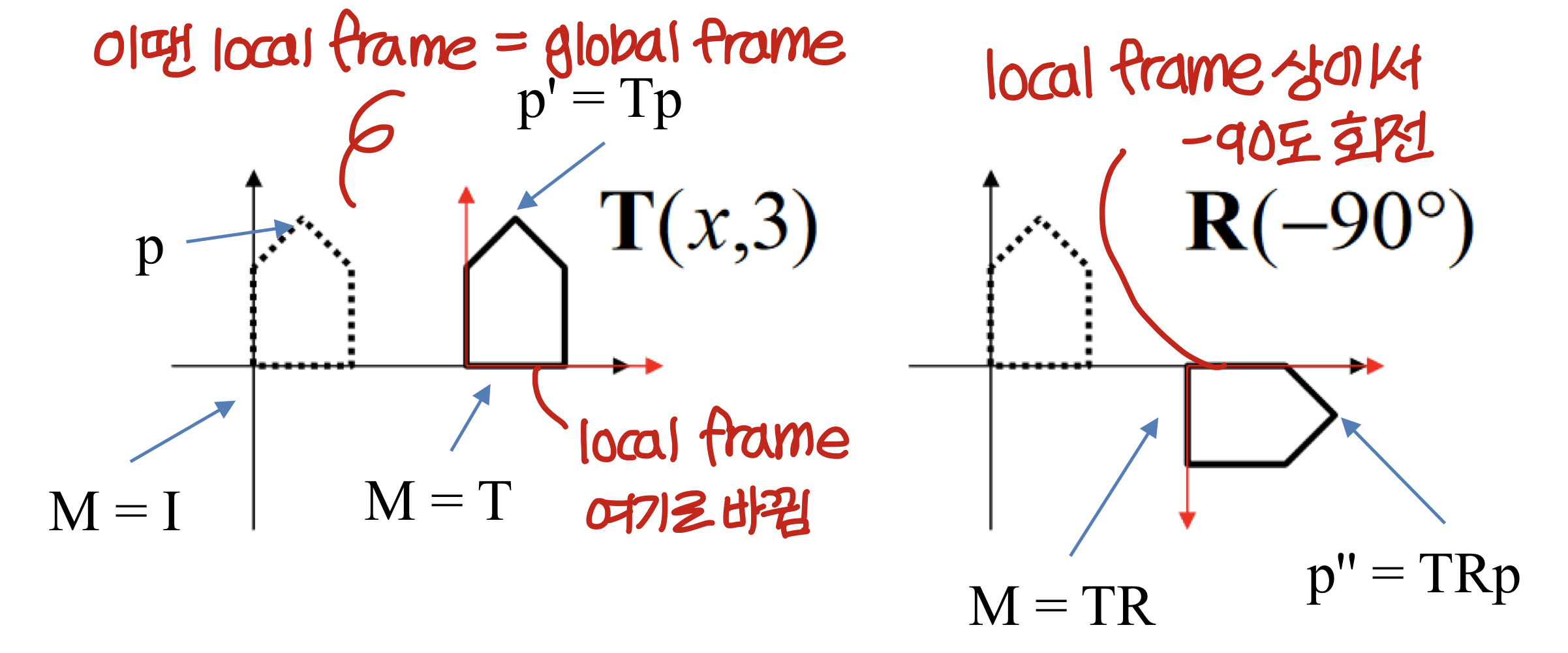
- OpenGL Function (glTranslate, glRotate 안에 넣어주는 건 local frame에 대해 표현된거. 그래서 오른쪽에 곱해준다.)
- glVertex에 넣어준 값은 "OpenGL Function으로 바뀐 local frame"에 대해 표현된거
Interpretation of a Series of Transformations #1
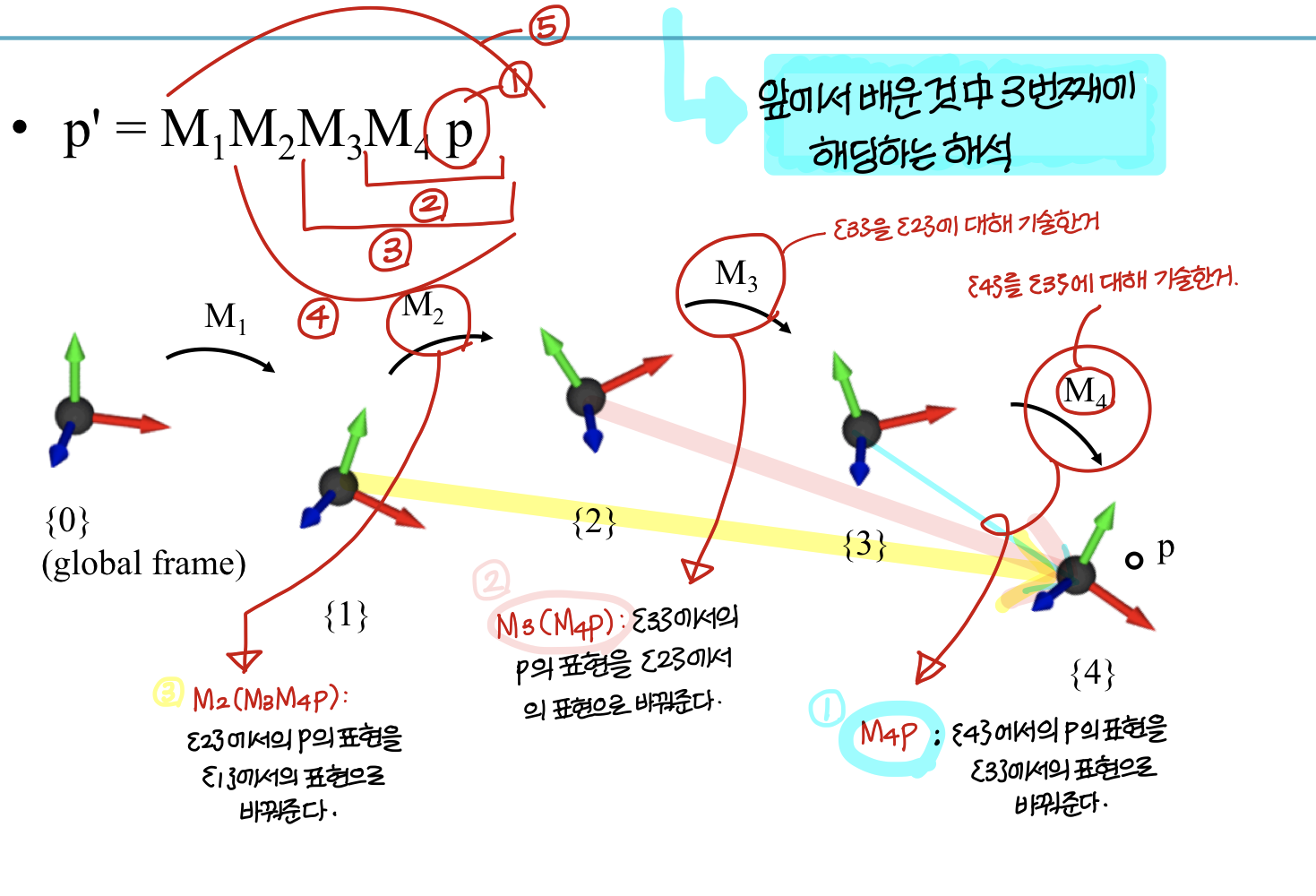
→ 오른쪽에서 왼쪽으로 해석한다고 무조건 global frame에 대한 해석은 아님.
→ 이렇게 local frame에 대한 해석으로도 볼 수 있음. (물론 곱하는 matrix는 local frame에 대해 기술한거)
(근데 이렇게 생각하면 헷갈리니까 왼쪽으로 갈수록 global에 가까운 matrix, 오른쪽에 갈수록 local에 가까운 matrix가 곱해진진거라고 보는게 맞음.)
Interpretation of a Series of Transformations #2
앞에서 배운것중 두번째에 해당하는 해석. 새로운 affine frame 정의한 다음, 그 affine frame 상에서 점을 콕 찍는 느낌.
물론 곱하는 matirx가 새로운 affine frame을 정의한는거긴 하지만
점까지 곱했을때 나타나는 결과는 global 상의 좌표임
이런식으로 local frame을 정의할 수 있다. 그리고 거기에다가 local frame 상의 좌표 곱하면 global frame 상의 좌표를 구할 수 있다.
[Practice] Interpretation of Composite Transformations

Quiz #2

→ 만약 왼→오로 해석했으면 결과는 A가 기술된 frame 기준 좌표
→ 만약 오→왼로 해석했으면 A, B, C가 기술된 frame 기준 좌표
Hierarchical Modeling
Hierarchical Modeling
→ 계층적
→ 어떤 부분이 부모에 종속되어 있다고 생각하고 변환을 시킬 수 있다.
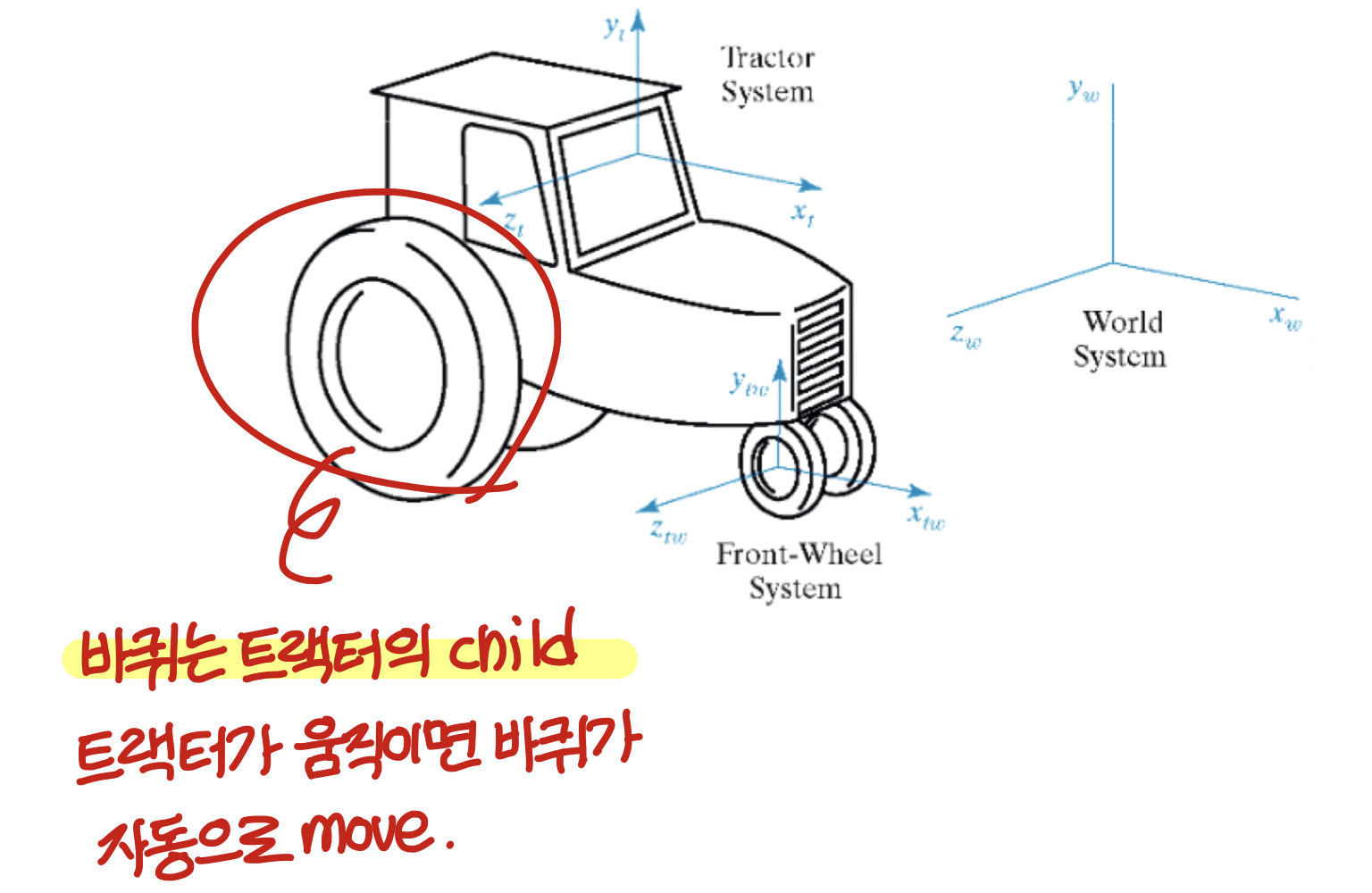
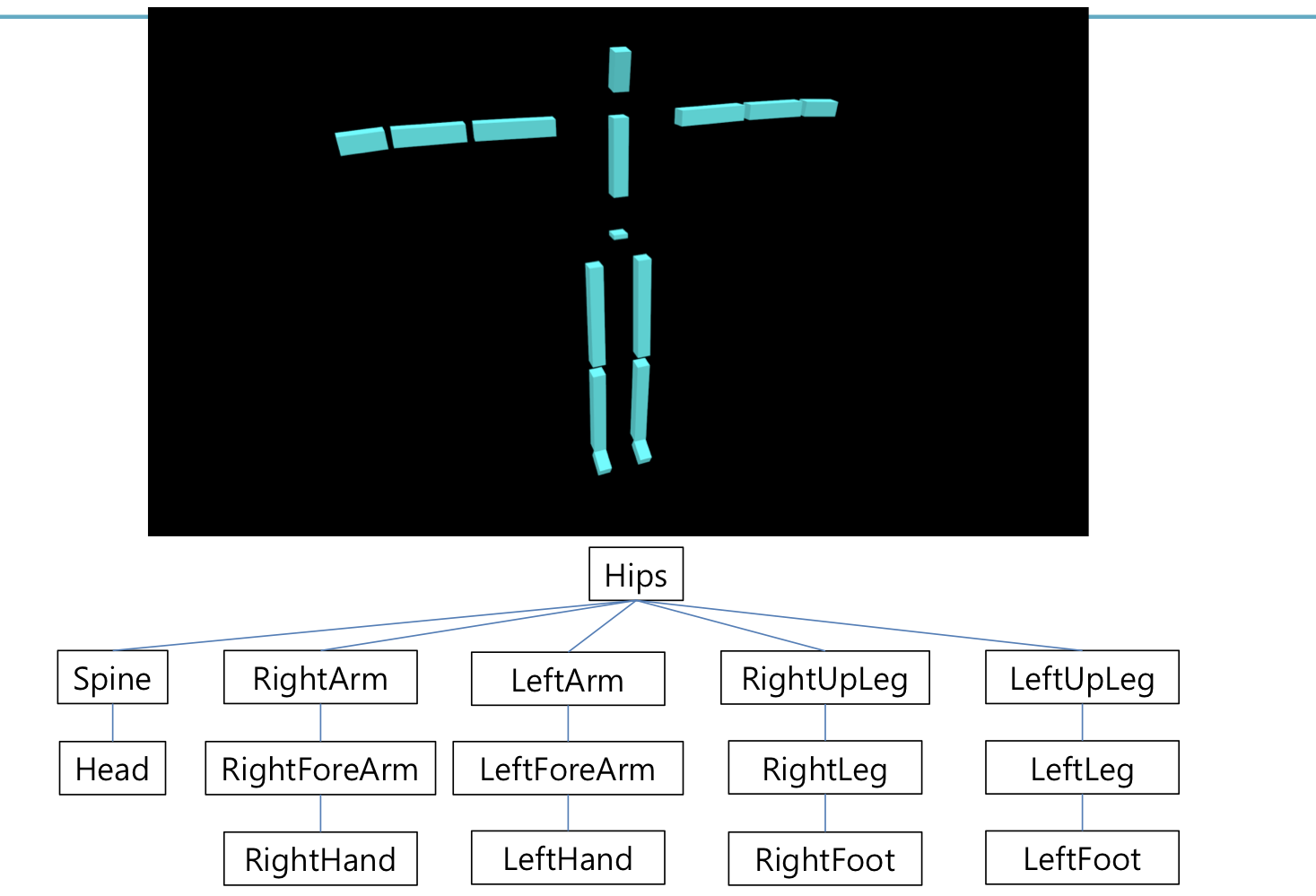
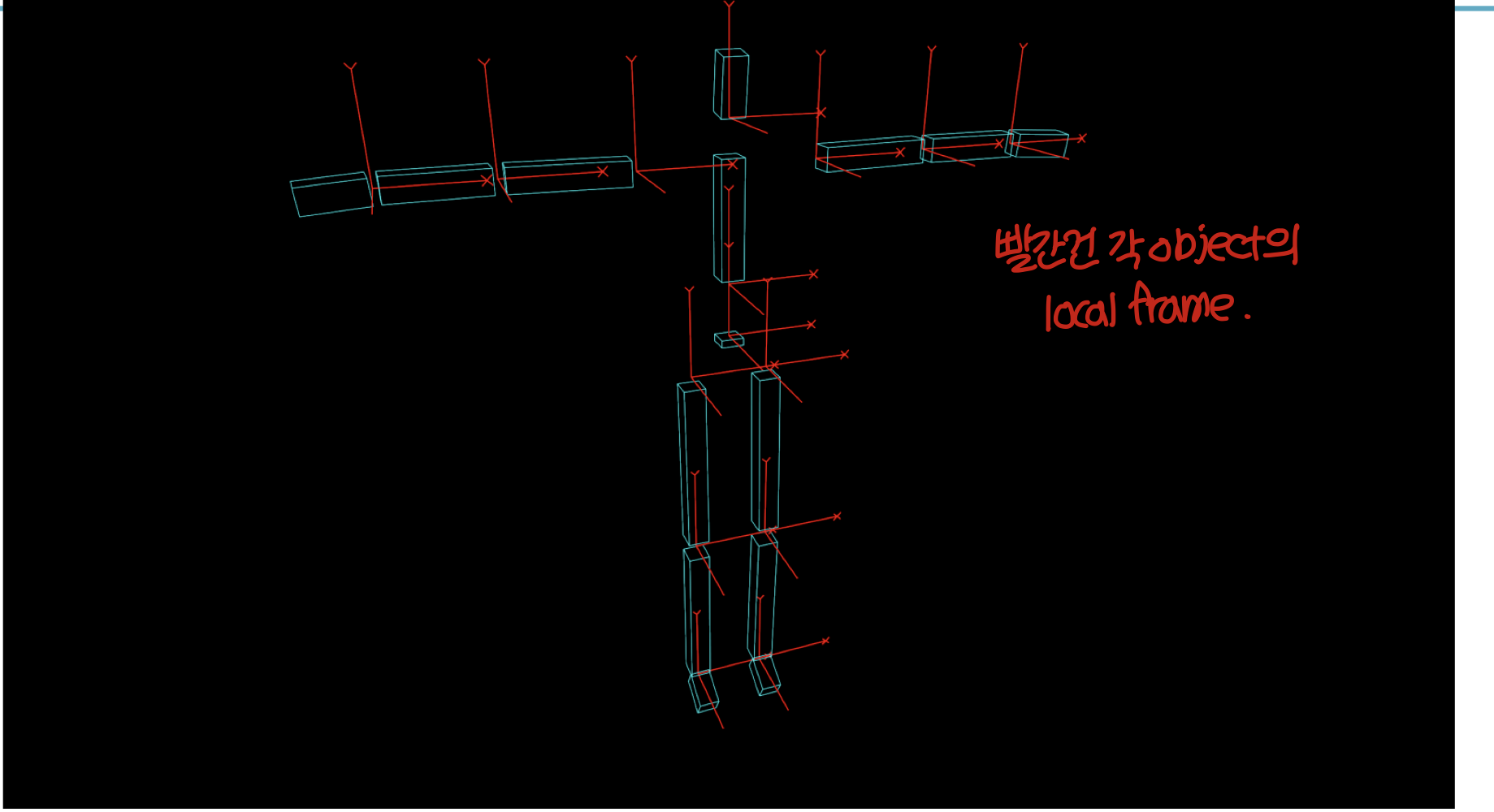
Articulated Body
→ Articulated Body (다관절체): body가 여러개의 part로 구성되어 있고 joint로 연결되어 있다.
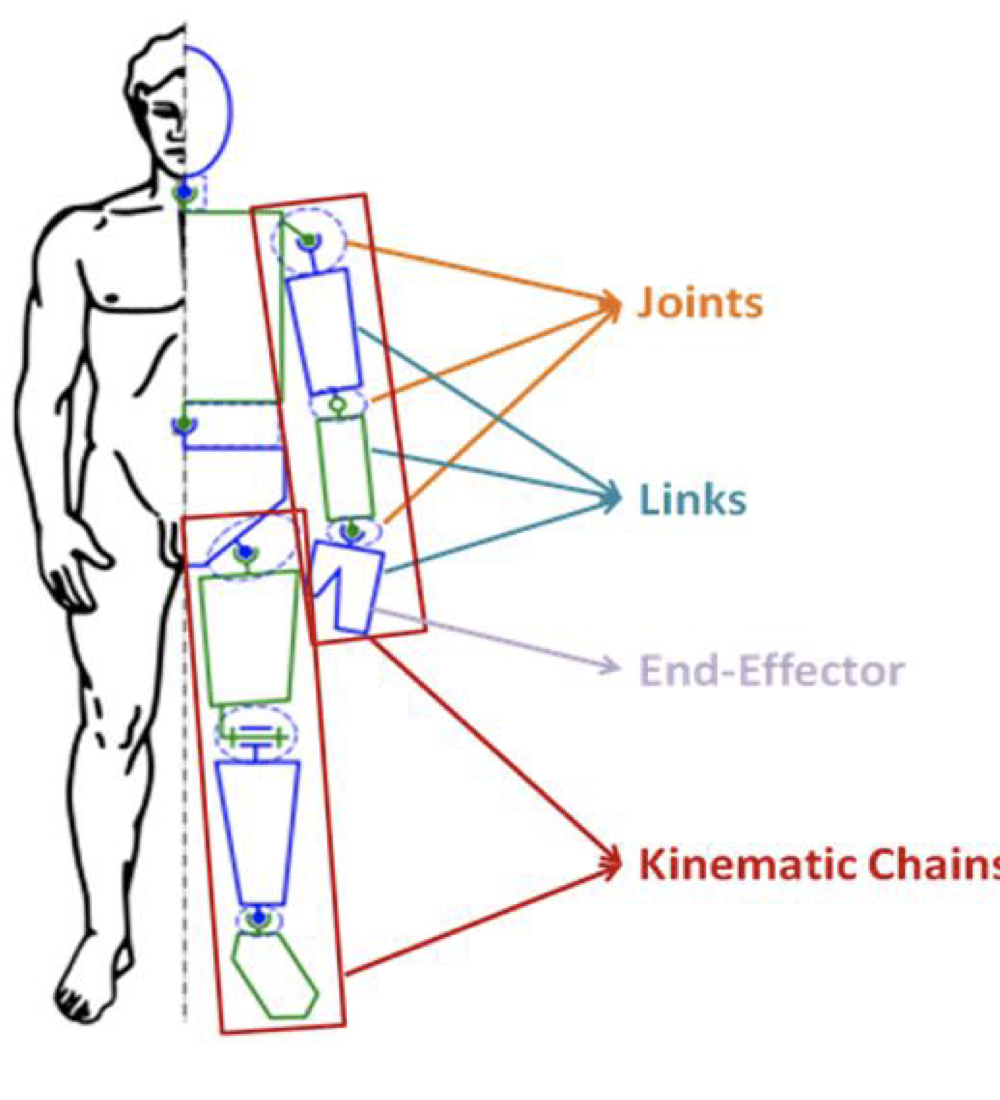
- Terminlogies
→ Joint: 두 object를 잇는 connection. some motion을 허용한다.
→ Link: joints 사이에 있는 rigid object
→ End effector: kinematic chain의 맨 끝에 있는거
→ articulated body는 graph structure로 표현된다. (제일 많이 사용되는게 tree structure)
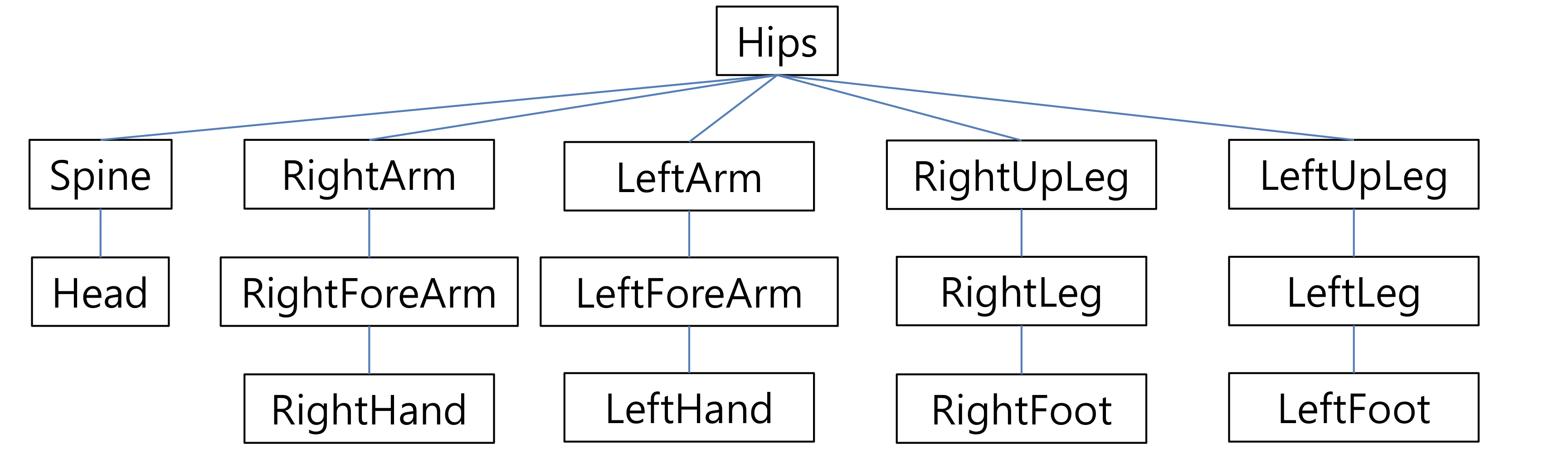
→ 각 node는 parent's node frame에 대해 기술된 transformatation을 가지고 있다.
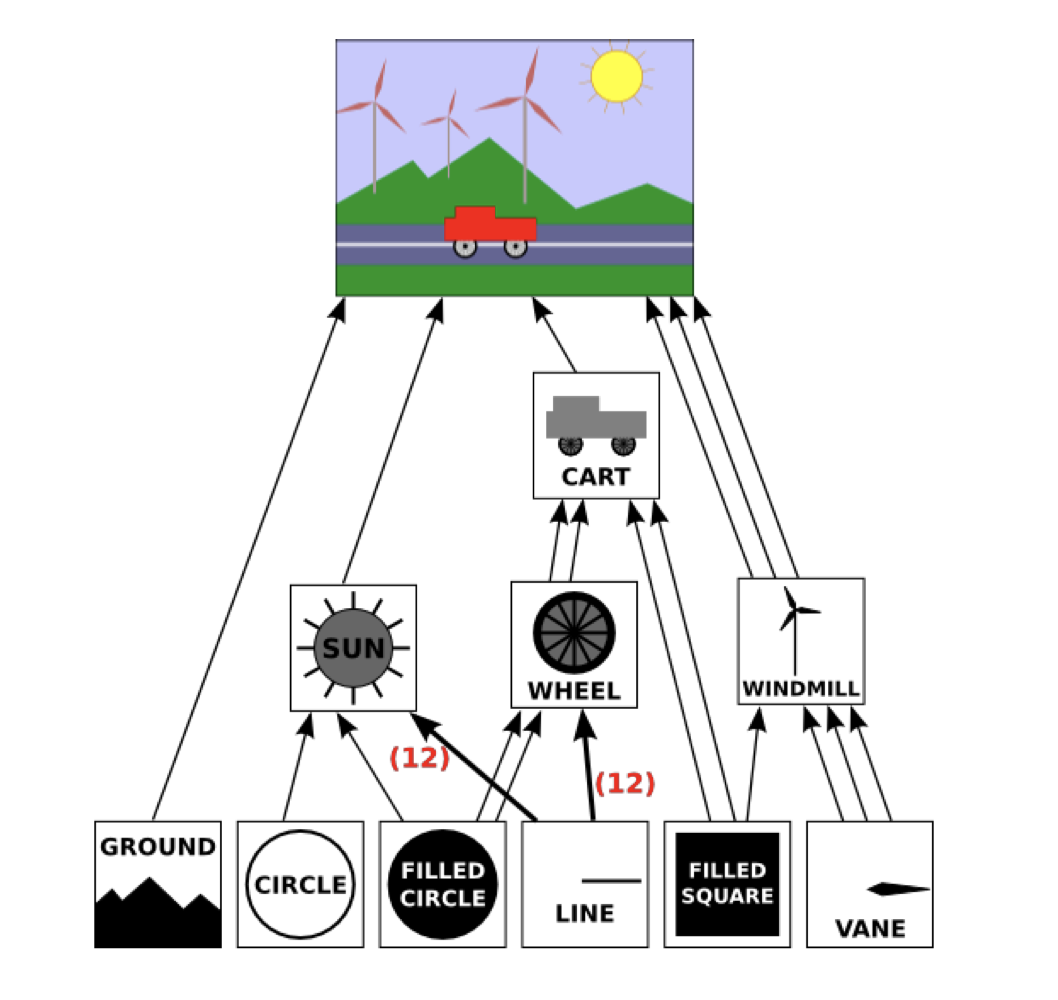
Scene Graph
→ hierarchical modeling은 scene 전체를 표현할 때도 사용된다.
→ scene graph는 entire scene을 표현하는 graph structure
→ 장면 자체가 root임
Rendering Hierarchical Models in OpenGL
→ OpenGL에서는 hierarchical structure로 drawing objects를 하기 위해 편리한 방법을 제공한다.
→ Matrix stack
OpenGL Matrix Stack
→ OpenGL Matrix Stack은 transformation matrices를 위한 stack임
→ current transformation matrix를 save하고 objects 그린 다음에 restore 하는 것이 가능하다.
- glPushMatrix()
→ stack에 current matrix를 push한다.
- glPopMatrix()
→ stack의 맨 위에 있는걸 뺀다.
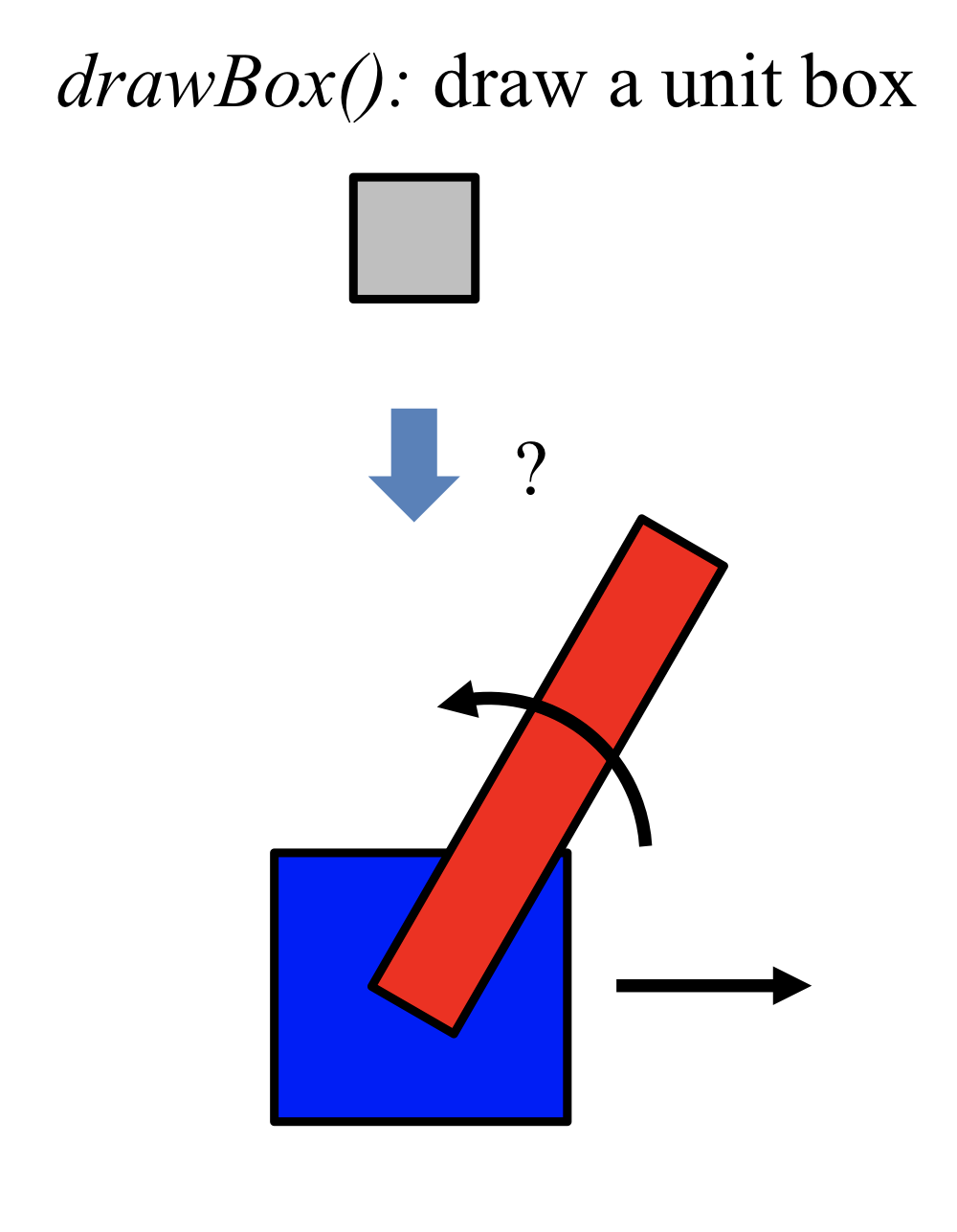
A simple example
→ unit box 하나를 그리는 drawBox() 를 사용해 밑에껄 만들고 싶음
→ 빨간게 파란박스 중심으로 돌아가는건 아니고(파란 박스 움직인다고 빨간박스 움직이지 않음)
그냥 우연히 좌표가 같은거
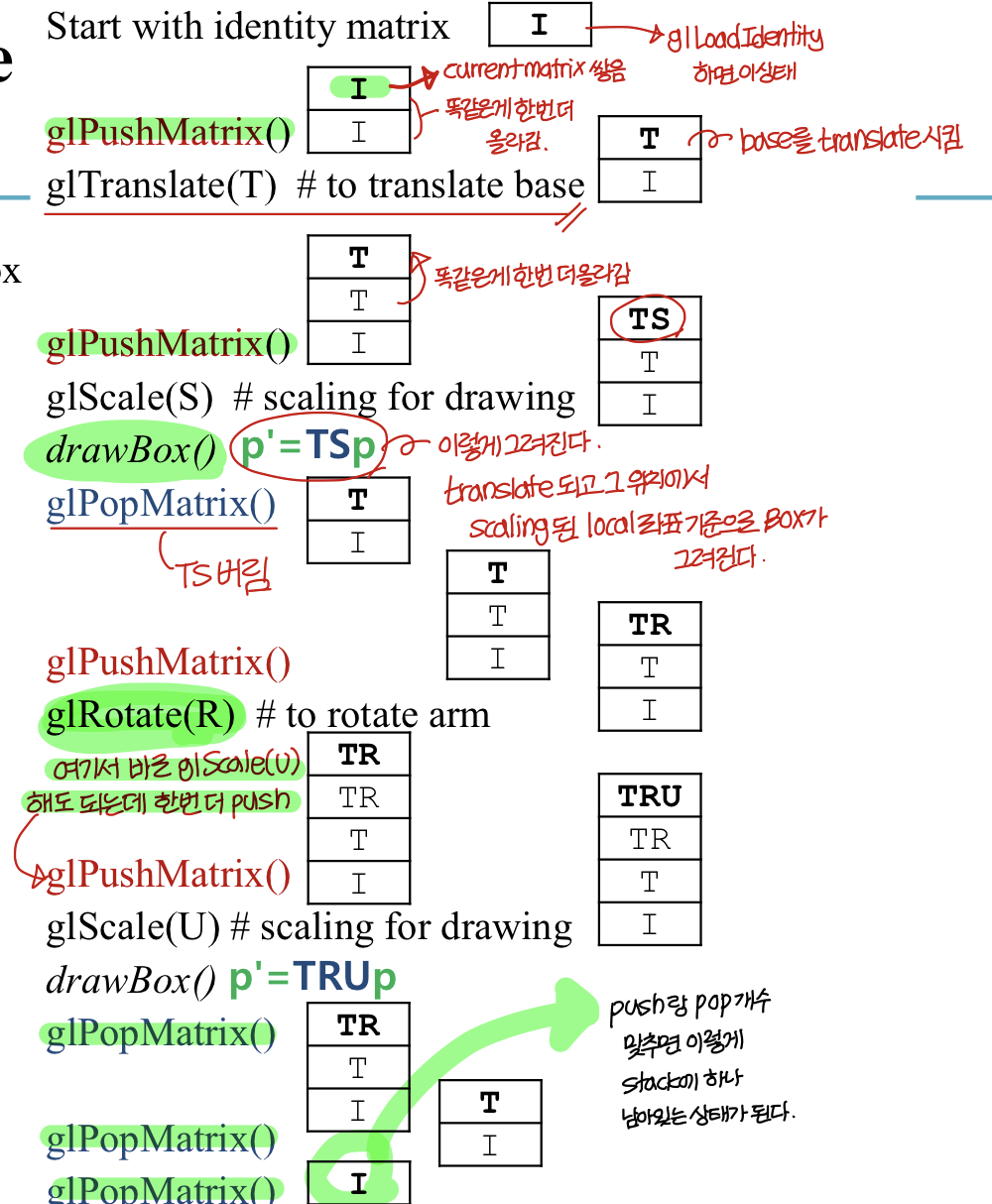
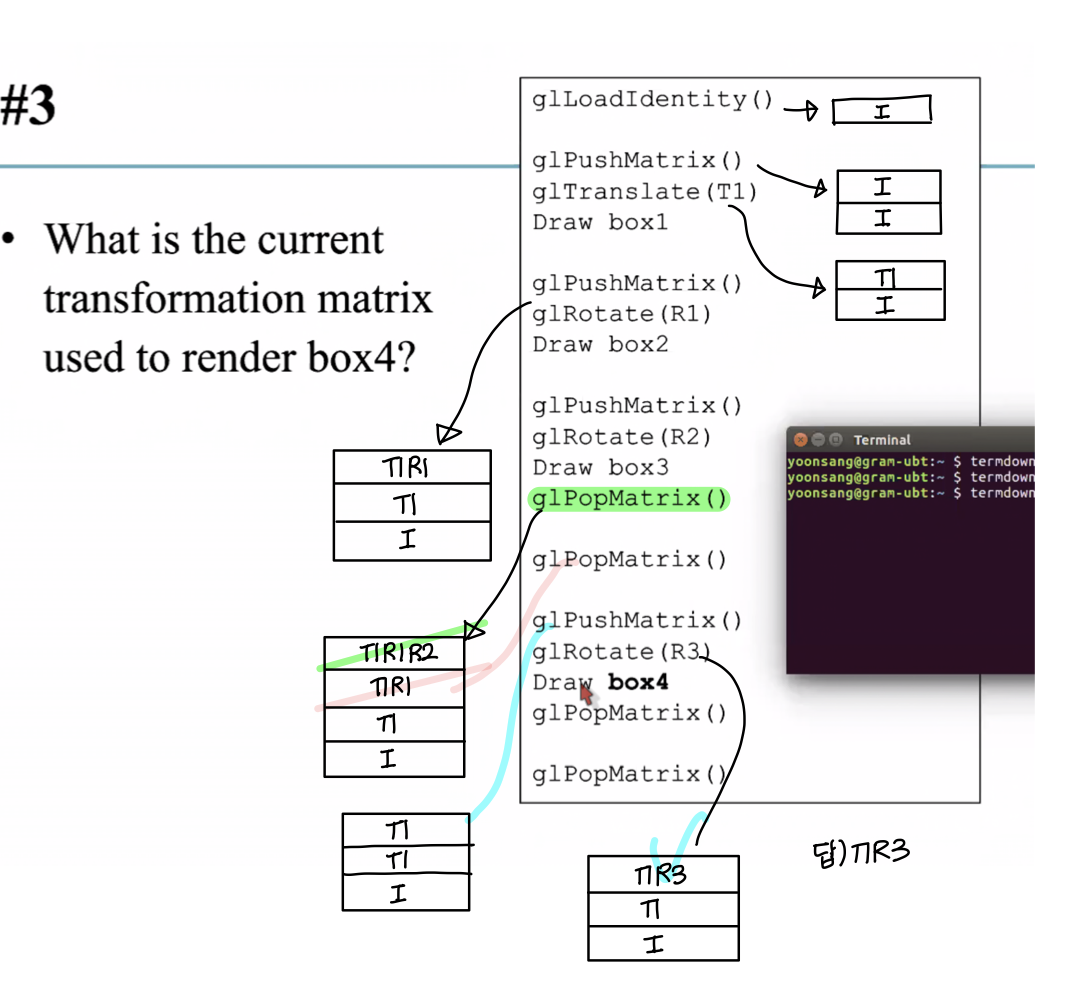
[Practice] Matrix Stack

Quiz #3
OpenGL Matrix Stack Type
<matrix type에 4가지가 있다.>
—- 위에 2개는 신경써야함 —-
- Modelview matrix stack (GL_MODELVIEW)
→ modelview matrix를 store한다.
→ 디폴트타입임 (우리가 이때까지 썼던거)
→ Modeling & viewing transformation function (gluLookAt(), glTranslate()...)같은건 glMatrixMode(GL_MODELVIEW)
와 함께 써야한다. (안지키면 잘못된 결과를 얻음)
- Projection matrix stack (GL_PROJECTION)
→ projection matrix를 store한다.
→ Projection transformation functions(gluPerspective(), glOrtho())은 glMatrixMode(GL_PROJECTION)과 함께 써야함
(안지키면 잘못된 결과를 얻음)
-— 밑에 2개는 신경 안써도 된다 —-
- Texture matrix stack(GL_TEXTURE)
- Color matrix stack(GL_COLOR)
<common guide>

→ gluPerspective 나 glOrtho 쓸때는 glMatrixMode(GL_PROJECTION) + glLoadIdentity() 앞에 써야함
→ gluLookAt이나 glTranslate, glScale(), glRotate 쓸때는 앞에 glMatrixMode(GL_MODELVIEW) + glLoadIdentity() 써야함
[Practice] With Correct Matrix Stack Types
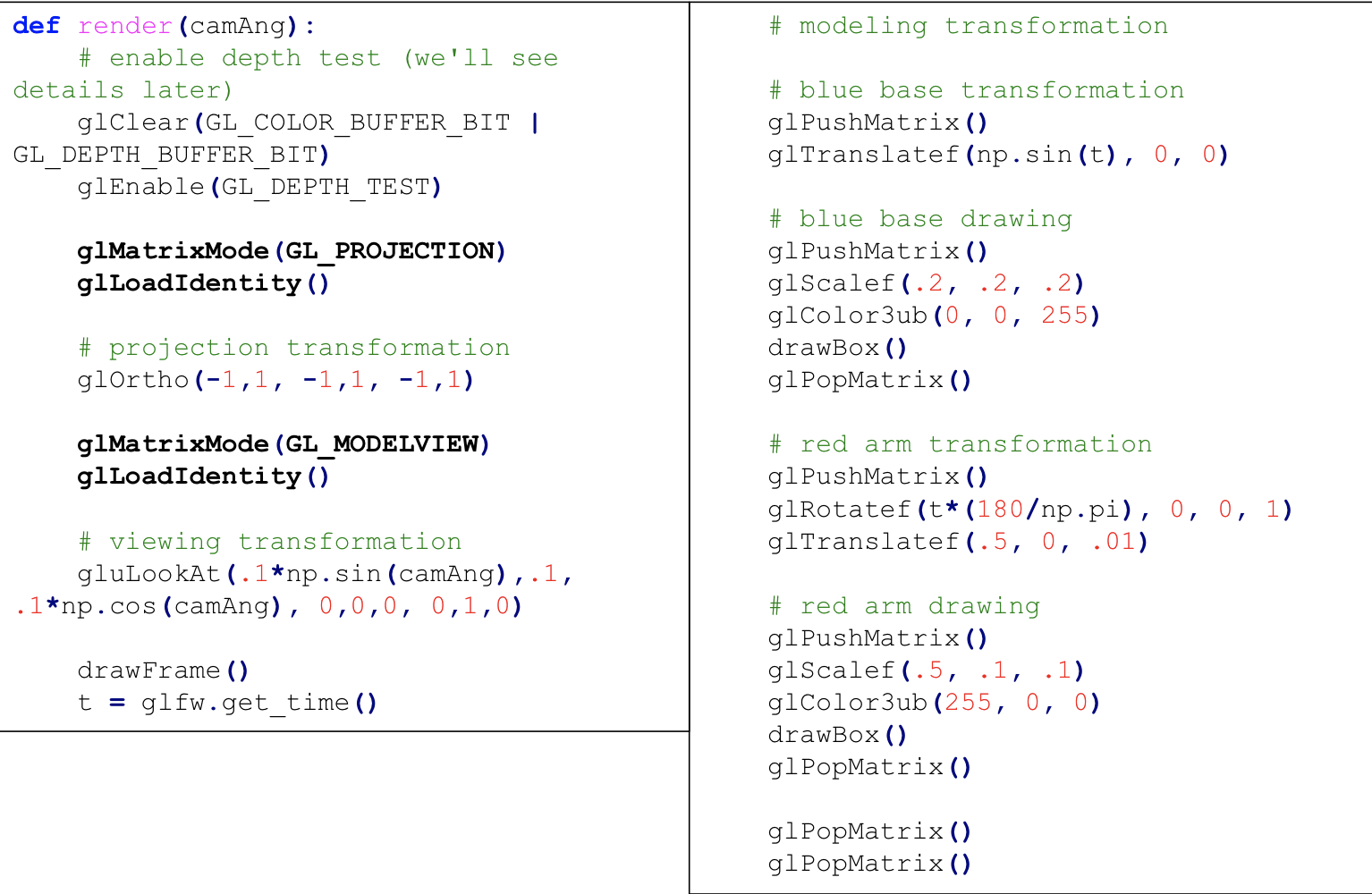
Uploaded by N2T