Coordinate System & Reference Frame (진심 노이해)
- Coordinate system
→ 포인트의 위치를 unique하게 기술하기 위해 한 개 이상의 숫자를 사용하는 시스템
→ 수학적 개념. 관찰된 점의 위치를 기술하기 위한 language라고 생각하면 된다.

- Reference frame
→ "추상적인 coordinate system"과 "실제로 물리적으로 존재하는 reference point"를 합친 개념이다.
→ 여기서 point는 coordinate system의 위치를 정의하는 point
→ 물리적 개념이다. 어떤 움직임의 상태를 기술하기 위한거

→ coordinate system이 각 reference frame에서의 움직임을 기술하기 위해 사용되는 language라고 생각하면 된다.
→ 두 용어 뉘앙스 다르긴 한데 혼용된다!!!
Global & Local Coordinate System(or Frame)
- Global coordinate system(or Global frame)
→ world에 붙어있는 coordinate system(or frame)
→ world coordinate system 또는 fixed coordinate system이라고도 부른다.
- Local coordinate system(or Local frame)
→ moving object에 붙어있는 coordinate system(or frame)
Rendering Pipeline
Rendering Pipeline
- 3차원에 장면을 구성하고 2D 화면으로 이를 본다. 그래서 3D scene 을 2D image로 바꿔야함
- 이를 graphics pipeline 이라고 한다.

→ 이때까지 우리가 배운건 vertex processing의 극초반 부분.
우리가 이번 수업과 다음 수업 때 다룰건 vertex processing 전체.
Vertex Processing
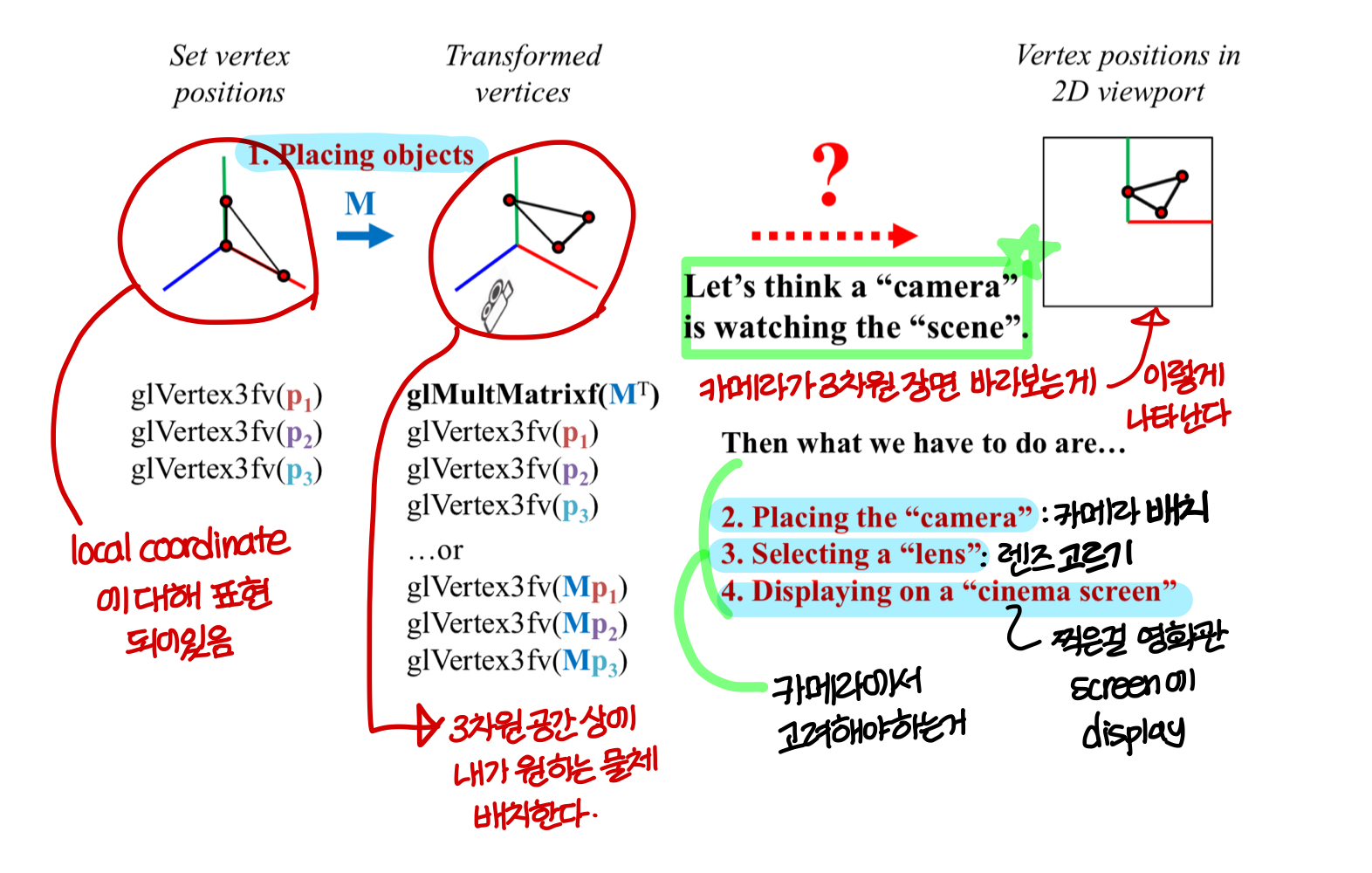
- Placing objects → Modeling transformation
- Placing the "camera" → Viewing transformation
- Select a "lens" → Projection transformation
- Displaying on a "cinema screen" → Viewport transformation
Vertex Processing(Transformation Pipeline)
→ transformation의 연속이라 transformation pipeline이라고도 부른다.

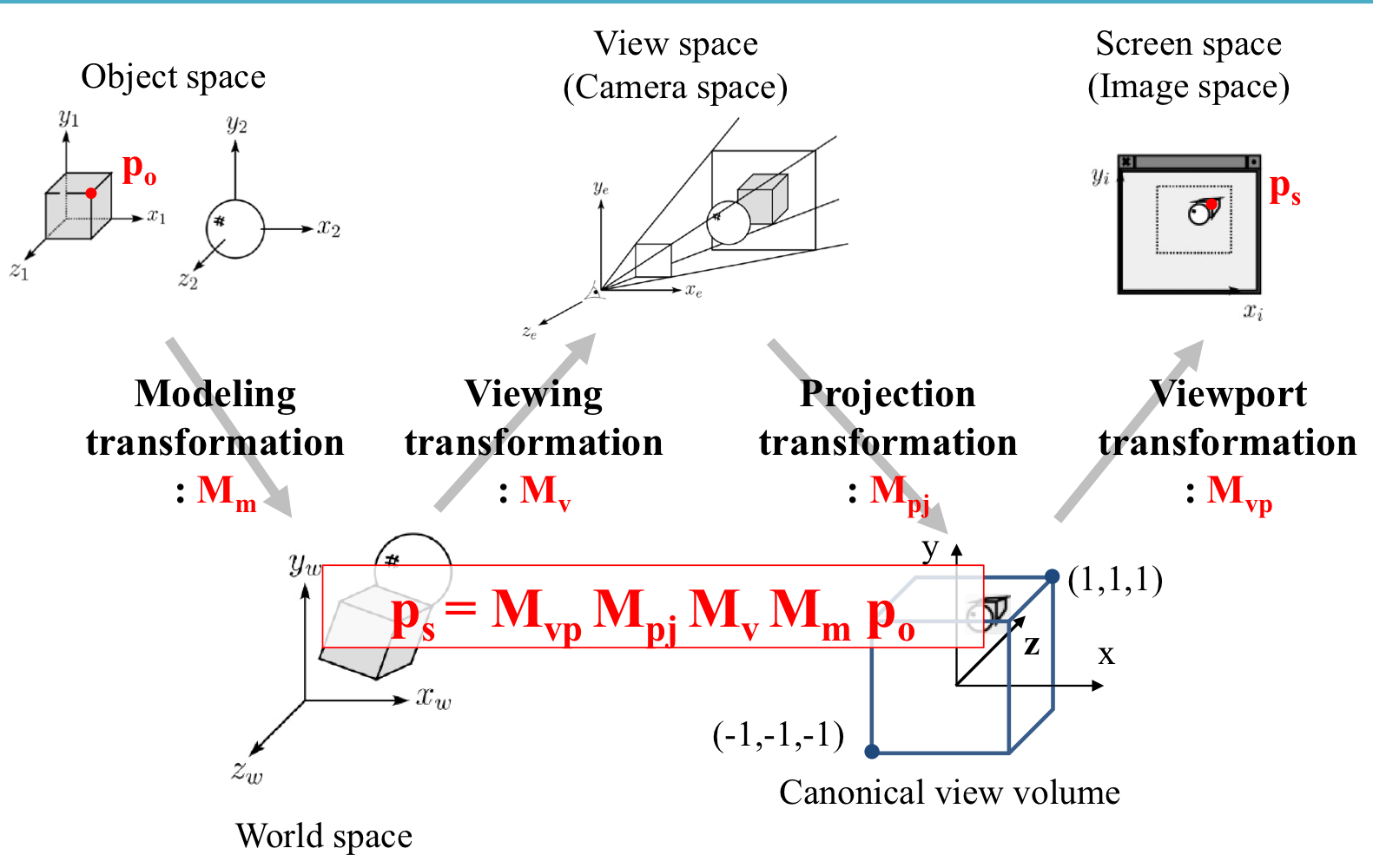
→ 각각의 matrix는 4X4
1. Modeling Transformation
- p_w = M_m @ p_0
- Geometry는 본래 object의 local coordinate에 대해 기술되어 있음
- world coordinate로 transform 하는 과정을 modeling matrix라고 부른다.
= M_m을 곱하는 것
- M_m은 Affine transformation으로 이루어져있다. (Translate, rotate, scale...)
Quiz #1

2. Viewing Transformation
- p_v = M_v @ p_w
- M_v는 Rigid transformation으로 이루어져있음 (Translate와 Rotate)
→ M_V는 viewing matrix라고 부른다.
- Viewing Transformation은 2가지로 나누어서 생각할 수 있다.
- 카메라 Placing 하는 과정 → How to set camera's position & orientation
- 카메라 입장에서(from the camera's point of view) vertex들을 표현하는거 → How to define the camera's coordinate system(frame)?
Viewing Transformation - 1. Setting Camera's Position & Orientation
카메라를 placing하는 여러가지 방법이 있음. 가장 직관적인 방법 중 하나는 다음 3가지로 나타내는거
- Eye point : Position of the camera
- Look-at point : camera의 target
- Up vector: 카메라의 위쪽방향(수직일 필요가 없다)
Viewing Transformation - 2. Defining Camera's Coordinate System
- eye point, look-at point, up vector 정해지면 우리는 camera frame을 얻을 수 있다. (P_eye, u, v, w)

- gluLookAt(eye_x, eye_y, eye_z, at_x, at_y, at_z, up_x, up_y, up_z) 함수 사용하면
viewing matrix를 생성하고 current matrix의 오른쪽에 곱한다. C ← C @ M_v
[Practice] gluLookAt()
import glfw
from OpenGL.GL import *
from OpenGL.GLU import * # OpenGL일때 이걸 하더라
import numpy as np
gCamAng = 0.
gCamHeight = .1
def render():
# enable depth test (나중에 배운다.)
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
glEnable(GL_DEPTH_TEST)
glLoadIdentity()
# use orthogonal projection (나중에 배운다.)
glOrtho(-1, 1, -1, 1, -1, 1)
# rotate "camera" position
gluLookAt(.1*np.sin(gCamAng), gCanHeight, 1*np.cos(gCamAng), 0, 0, 0, 0, 1, 0)
drawFrame()
glColor3ub(255, 255, 255)
drawTriangle()
def drawFrame():
glBegin(GL_LINES)
glColor3ub(255, 0, 0)
glVertex3fv(np.array([0., 0., 0.]))
glVertex3fv(np.array([1., 0., 0.]))
glColor3ub(0, 255, 0)
glVertex3fv(np.array([0., 0., 0.]))
glVertex3fv(np.array([0., 1., 0.]))
glColor3ub(0, 0, 255)
glVertex3fv(np.array([0., 0., 0.]))
glVertex3fv(np.array([0., 0., 1.]))
glEnd()
def drawTriangle():
glBegin(GL_TRIANGLE)
glVertex3fv(np.array([.0, .5, .0]))
glVertex3fv(np.array([.0, .0, .0]))
glVertex3fv(np.array([.5, .0 ,.0]))
glEnd()
def key_callback(window, key, scancode, action, mods):
global gCamAng, gCamHeight
if action == glfw.PRESS or action == glfw.REPEAT:
if key == glfw.KEY_1:
gCamAng += np.radians(-10)
elif key == glfw.KEY_3
gCamAng += np.radians(10)
elif key == glfw.KEY_2
gCamHeight += .1
elif key == glfw.KEY_W
gCamHeight += -.1
def main():
if not glfw.init():
return
window = glfw.create_window(640, 640, 'gluLookAt()', None, None)
if not window:
glfw.terminate()
return
glfw.make_context_current(window)
glfw.set_key_callback(window, key_callback)
while not glfw.window_should_close(window):
glfw.poll_events()
render()
glfw_swap_buffers(window)
glfw.terminate()
if __main__ == "__main__":
main()

Moving Camera vs Moving World
사실 다음은 같은 operatio 이다.
- Translate camera by (1, 0, 2) = Translate world by (-1, 0, -2)
- Rotate camera by 60도 about y = Rotate world by -60도 about y
→ 그래서 카메라를 움직이는 대신에 glRotate()와 glTranslate()를 써도 된다.
→ gluLookAt()을 쓰는건 카메라를 조작하는 많은 방법 중 하나일 뿐이다.
→ Default로 OpenG의 카메라는 origin에 있고 negative z 방향으로 pointing 하고 있다.
(그래서 아무 설정안하면 2차원으로 보이는구나.)

Modelview Matrix
- 위에서 말했듯이 카메라를 움직이는것과 world를 움직이는 것은 완전히 동일한 opeation이다.
- 그래서 OpenGL에서는 Viewing Matrix M_v와 modeling matrix M_m를 합쳐서
M = M_v @ M_m 을 modelview matrix라고 한다.
Quiz #2

만약에 (0, 0, -1, 0, 0, 0, 0, 1, 0) 으로 하면 삼각형이 y축 기준으로 뒤집힌것처럼 보인다 .
만약에 (0, 0, 1, 0, 0, 0, 0, 1, 0) 으로 하면 같은 결과가 나온다.
→ (지금 이 예시에서는 거리 인식을 안하기 때문에 차이를 보여주진 못하지만 정확하게 똑같은건 아니다.)
(0, 0, 0, 0, 0, 0, 0, 1, 0)으로 하면 안되는 이유는 → 카메라의 위치와 물체의 위치가 같기 때문
LabAssignment5


2번의 glRotatef()와 glTranslatef()를 사용해서 gluLookAt(3, 3, 3, 0, 0, 0, 0, 1, 0)과 같은 효과를 내는게 문제

3. Projection Transformation (렌즈를 고르는 과정)
Review:Normalized Device Coordinates
- 우리 [-1, -1] to [1. 1] 공간에 삼각형을 그렸다.
- 이 공간을 normalized device coordinates(NDC)라고 부른다.
- canonical view volume 이라고도 부른다.
→ coordinate과 volume은 다르지만, 이 둘은 같은 걸 의미할때 혼용되어 쓰인다.
Canonical View "Volume"
- [-1, -1] to [1, 1] 공간으로 알고 있었지만 사실 canonical view volume 은 3D cube이다.
[-1, -1, -1] to [1, 1, 1] in OpenGL
- xy plane이 우리가 실제로 보는 2D "viewport"이다.
- NDC in OpenGL은 left-handed coordinate system이라는걸 기억해라.
하지만 OpenGL의 projection function 들이 positive z 방향을 바꾸기 때문에
view, world(model?), camera space는 right-handed coordinate system이다.
(만약 OpenGL이 제공하는 projection function을 쓰지 않는다면 처음부터 왼손좌표계를 쓸 수 있다.)
- OpenGL은 canonical view volume 안에 있는 것만 그린다. 왜?
1) 카메라 시야 안에 있는것만 그리기 위해 (카메라의 시야 밖에 있는 것은 canonical view volume 안에 안들어온다.)
2) 카메라에 너무 멀리 있거나 너무 가까이 있는건 그리지 않기 위해 (무한히 많은 것들을 그리는게 아니라 범위 설정하는 느낌)
항상 사이즈가 2인 view volume(visible volume)을 써야하나?
- view volume과 canonical view volume은 다른거임
- 답은 "No" → 원하는 사이즈와 모양으로 만들 수 있다.
"frustums"(절두체, 사각뿔 끄트머리 자른거) 이 모양으로도 만들 수 있다.
<Projection transformation>
- visible volume 안에 있는 모든것들은 canonical view volume으로 맵핑(projected) 된다.
- Canonical view volume 안에 있는 3D point 들은 xy plane의 2D point로 projected 된다.
Projection in General
- General definition: N차원 공간에 있는걸 m차원 공간으로 옮기는거 (m<N)
Projection in Computer Graphics
- 컴퓨터 그래픽스에선 3D coordinates를 2D scren coordinate로 mapping 하는 projection을 한다.
- 두 단계로 생각해볼 수 있다.
1) Map an aribitary view volume to canoncial view volume
2) canonical view volume에 있는 3D point를 xy plane으로 mapping (이때 z 값 필요없는게 아니다. depth test 때문에!)
- 자주 사용되는 projection method 2가지가 있다.
1) Orthographic projection
2) Perspective projection
Orthographic(Orthogonal) Projection
- View volume: Cuboid(직육면체)
카메라 위치 기준으로 (left, botton, -near)과 (right, top, -far) 명시
그럼 이 두 점을 이은 선이 대각선인 직육면체가 view volume 이다.
- Orthographic projection: cuboid view volume에 있는 애들을 canonical view volume으로 mapping 하는거
→ scaling 과 translation 로만 구성되어 있다.
→ scaling과 translation 으로만 구성된 transformation을 "windowing" transformation이라고 부른다.

Windowing Transformation

작은 직사각형에 있는 파란점을 큰 직사각형에 있는 빨간점으로 옮기는 과정이다.
1) 일단 원점으로 translate 하고 (왼쪽 아래점이 원점으로 가도록)
2) 크기가 같아지도록 scaling을 하고
3) 위치를 맞게 다시 옮긴다. (왼쪽 아래점의 위치가 맞도록)
Orthographic Projection Matrix
- 이거 곱해도 원근감 반영이 안된다.뒤에 있다고 더 작게 그려지지 않음
- 위에서 만든 matrix를 3차원으로 확대한걸 생각하면 된다.
- x_h = right, x_l = left (원래 직사각형)
x_h' = 1, x_l' = -1 (새로운 volume)
- y_h = top, y_l = botton (원래 직사각형)
y_h' = 1, y_l' = -1 (새로운 volume)
Examples of Orthographic Projection
Orthographic Projection 하면 멀리 있는거나 가까이 있는거나 똑같은 길이로 본다.
Properties of Orthographic Projection
- 사실적이지 않다. (원래 멀리 있는건 작게 보이는데 이건 그렇지가 않으니까)
- 정확한 측정을 할 때는 좋다.
- CAD 나 건축 drawing 처럼 정확한 측정이 중요한 곳에 많이 사용한다.
- orthogonal projection도 Affine transformation에 속한다. (scaling이랑 translate 으로만 이루어졌으니까)
Affine transformation은
1) 평행을 평행으로 유지
2) 비율 유지
3) 각도는 유지되지 않는다. (밑에 그림 직육면체 각 각도 모두 90도인데 그렇게 보이지 않는다.)
glOrtho()
- glOrtho(left, right, bottom, top, zNear, zFar)
→ 카메라 space 기준으로 view frame을 만드는거다. 그래서 카메라가 비스듬히 비추고 있으면 그게 반영이 된다.
→ 자주 사용되는 기능이라 GL에서 기능을 제공한다.
→ orthographic projection matrix를 만들어서 current transformation matrix의 오른쪽에 곱한다.
C ← CM_ortho
- zNear과 zFar의 부호
→ postive: 카메라 앞에 있는 plane (사실 방향 바뀌니까 - 붙어서 들어간다. 바뀐 space 기준으론 음수)
→ negative value: 카메라 뒤에 있는 plane
[Practice] glOrtho
import glfw
from Open.GL import *
from Open.GLU import &
import numpy as np
gCamAng = 0.
gCamHeight = 1.
#draw a cube of side 1, centered at origin
def drawUnitCube():
glBegin(GL_QUADS)
glVertex3f(0.5, 0.5, -0.5)
glVertex3f(-0.5, 0.5, -0.5)
~~~~
#이런식으로 사각형 8개 그려준다.
glEnd()
def drawCubeARray():
for i in range(5):
for j in range(5):
for k in range(5)
glPushMatrix()
glTranslatef(i, j, -k-1)
glScalef(.5, .5, .5)
drawUnitCube()
glPopMatirx()
def drawFrame()
glBegin(GL_LINES)
glColor3ub(255, 0, 0)
glVertex3fv(np.array([0., 0., 0.]))
glVertex3fv(np.array([1., 0., 0.]))
glColor3ub(0, 255, 0)
glVertex3fv(np.array([0., 0., 0.]))
glVertex3fv(np.array([0., 1., 0.]))
glColor3ub(0, 0, 255)
glVertex3fv(np.array([0., 0., 0.]))
glVertex3fv(np.array([0., 0., 1.]))
glEnd()
def render():
global gCamAng, gCamHeight
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
glEnable(GL_DEPTH_TEST)
#draw polygons only with boundary edges (색칠 안하고 겉에 선만 그리겠다는 말임)
glPolygonMode(GL_FRONT_AND_BACK, GL_LINE)
glLoadIdentity()
glOrtho(-5, 5, -5, 5, -10, 10)
#glOrtho(-5, 5, -5, 5, -1, 1) 이렇게 하면 잘려보인다. 꼭 실행시켜서 다시 확인해보기
#view volume이 기울어져있어서 안쪽이 잘린것처럼 보이지만 사실은 바깥쪽이 잘린거임
gluLookAt(1 * np.sin(gCamAng), gCamHeight, 1* np.cos(gCamAng), 0, 0, 0, 0, 1, 0)
drawFrame()
glColor3ub(255, 255, 255)
drawCubeArray()
def key_callback(window, key, scancode, action, mods):
glboal gCamAng, gCamHeight
if action == glfw.PRESS or action == glfw.REPEAT
if key == glfw.KEY_1:
gCamAng +=np.radians(-10)
elif key == glfw.KEY_3:
gCamAng +=np.raidans(10)
elif key == glfw.KEY_2:
gCamHeight += .1
elif key == glfw.KEY_W:
gCamHeight += -.1
def main():
if not glfw.init():
return
window = glfw.create_window(640, 640 'glOrtho()', None, None)
if not window:
glfw.terminate()
glfw.make_context_current(window)
glfw.set_key_callback(window, key_callback)
while not glfw.window_should_close(window):
glfw.poll_events()
render()
glfw.swap_buffers(window)
glfw.terminate()
if __name__ == "__main__"
main()
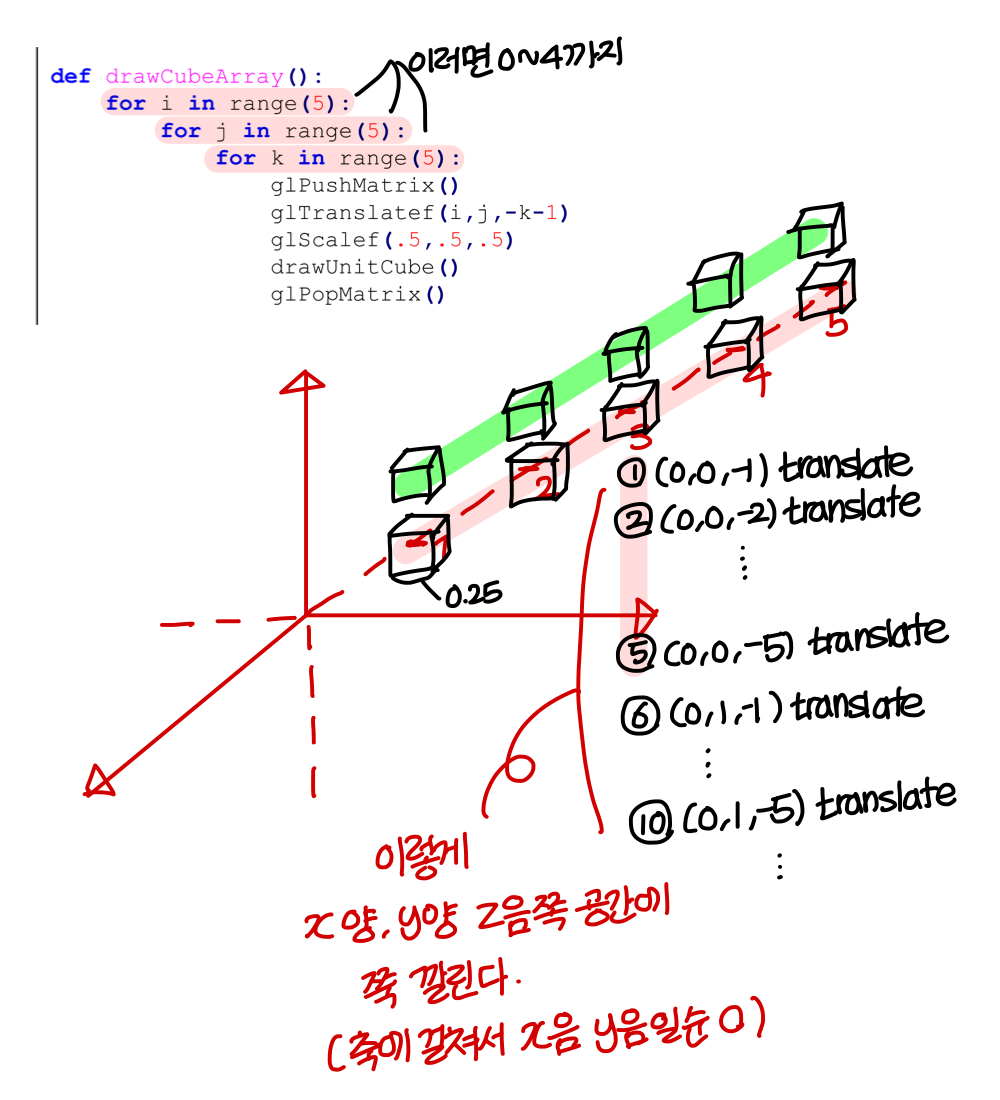
Quiz #3

Uploaded by N2T


