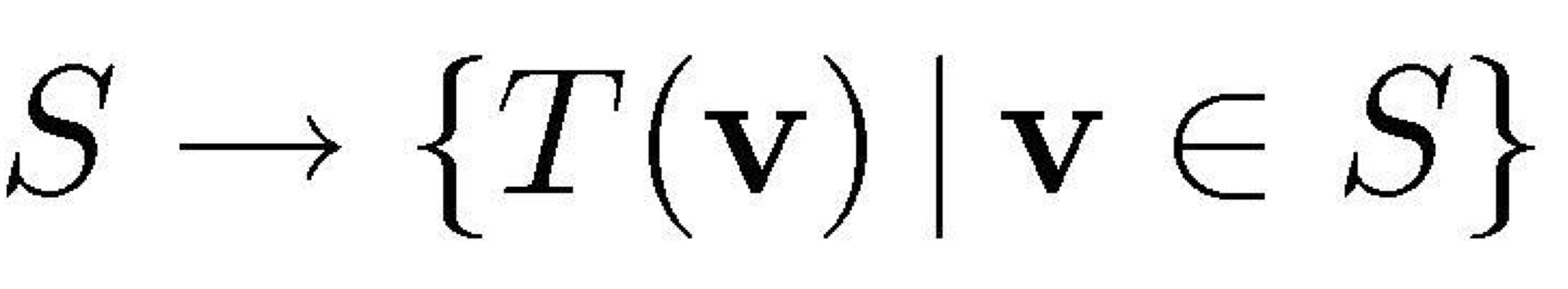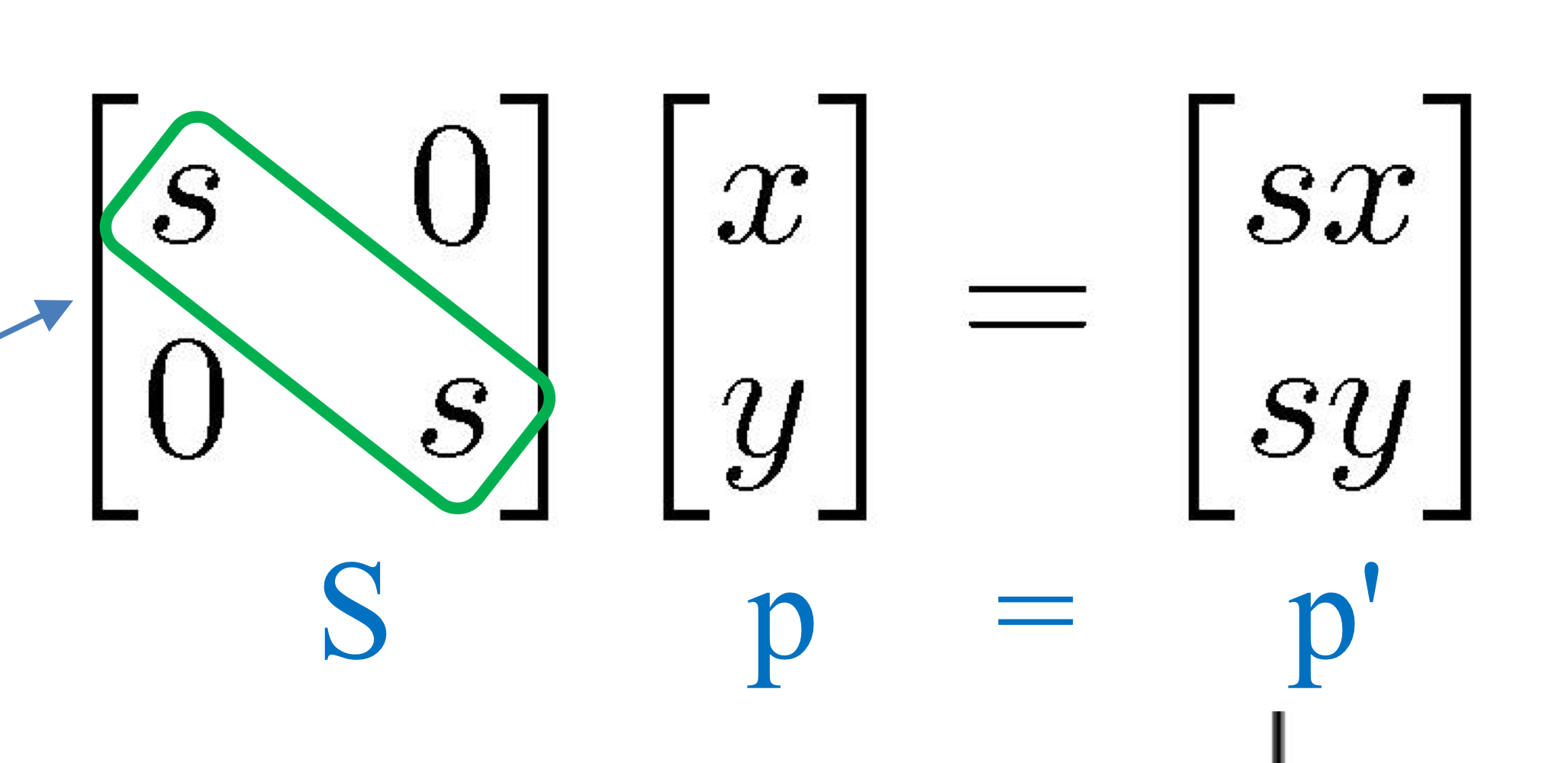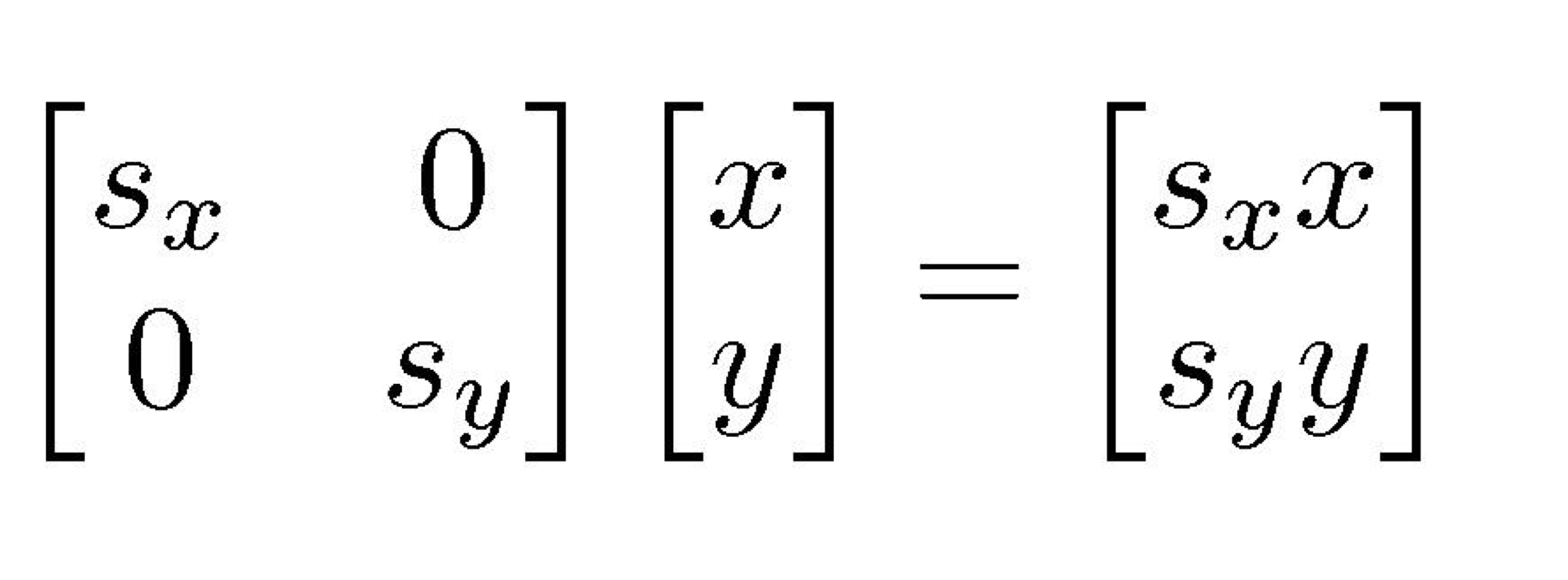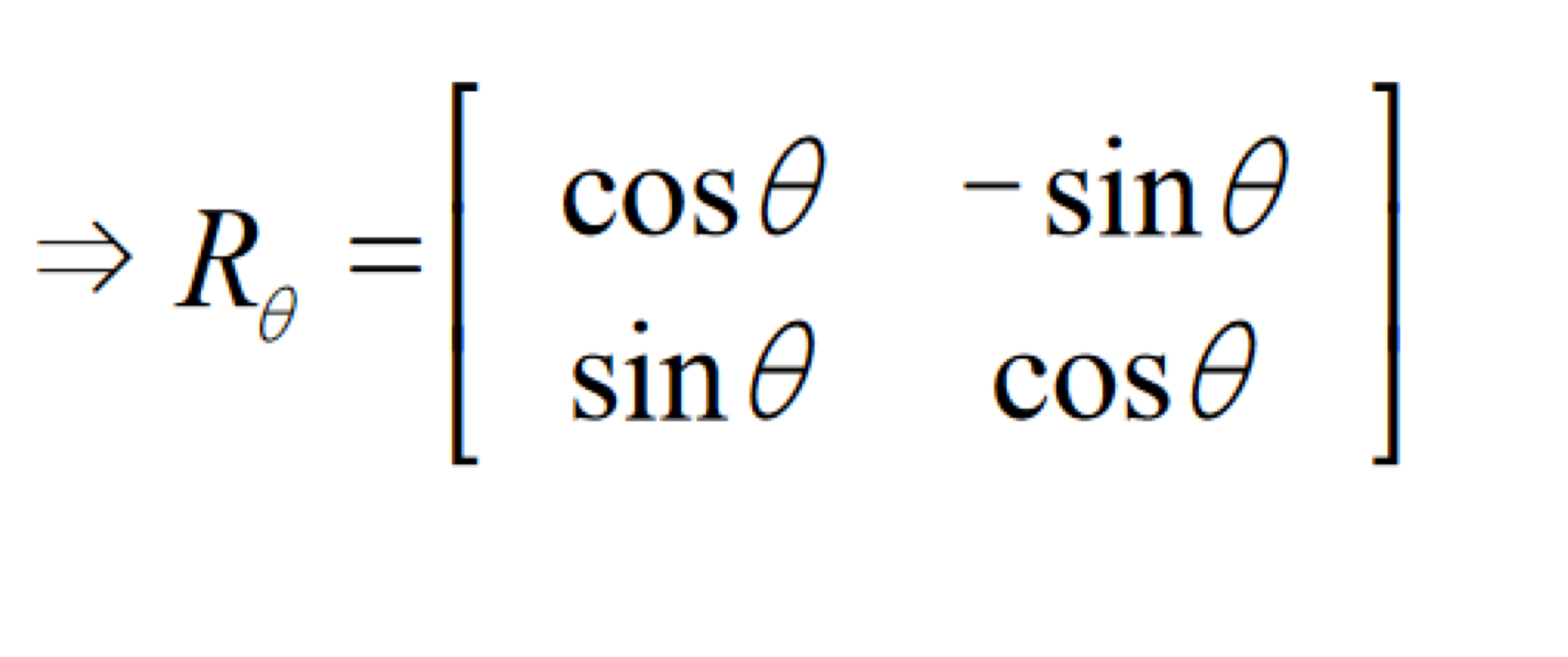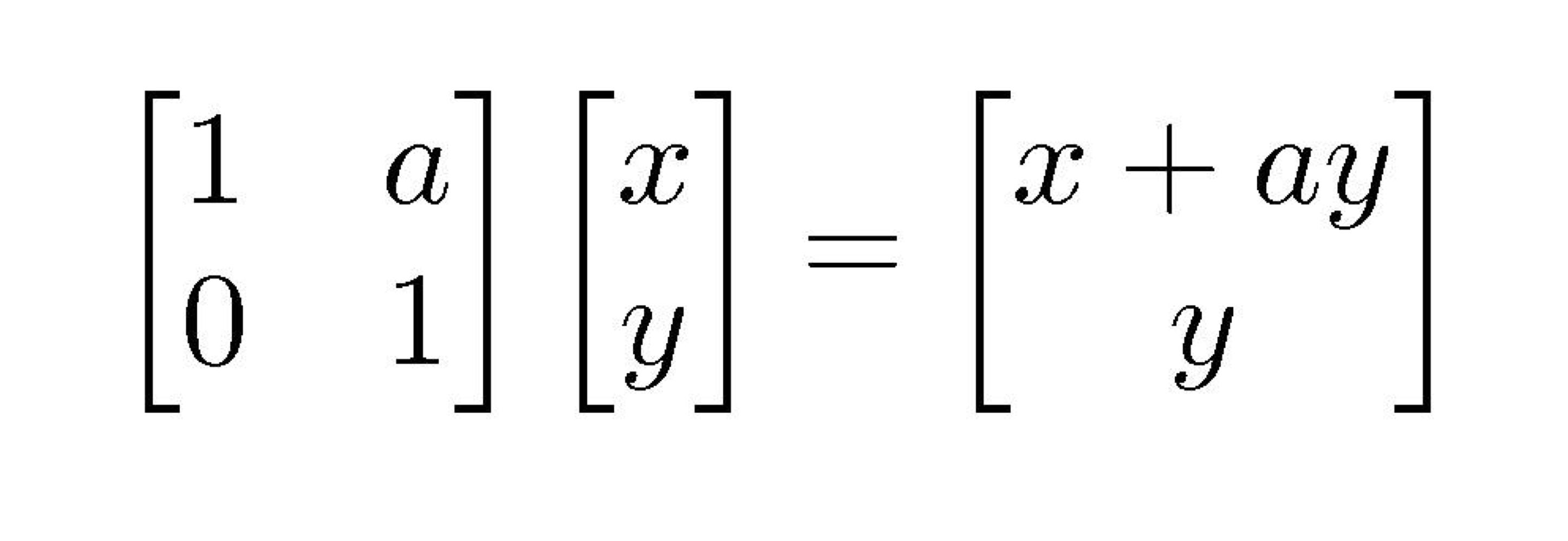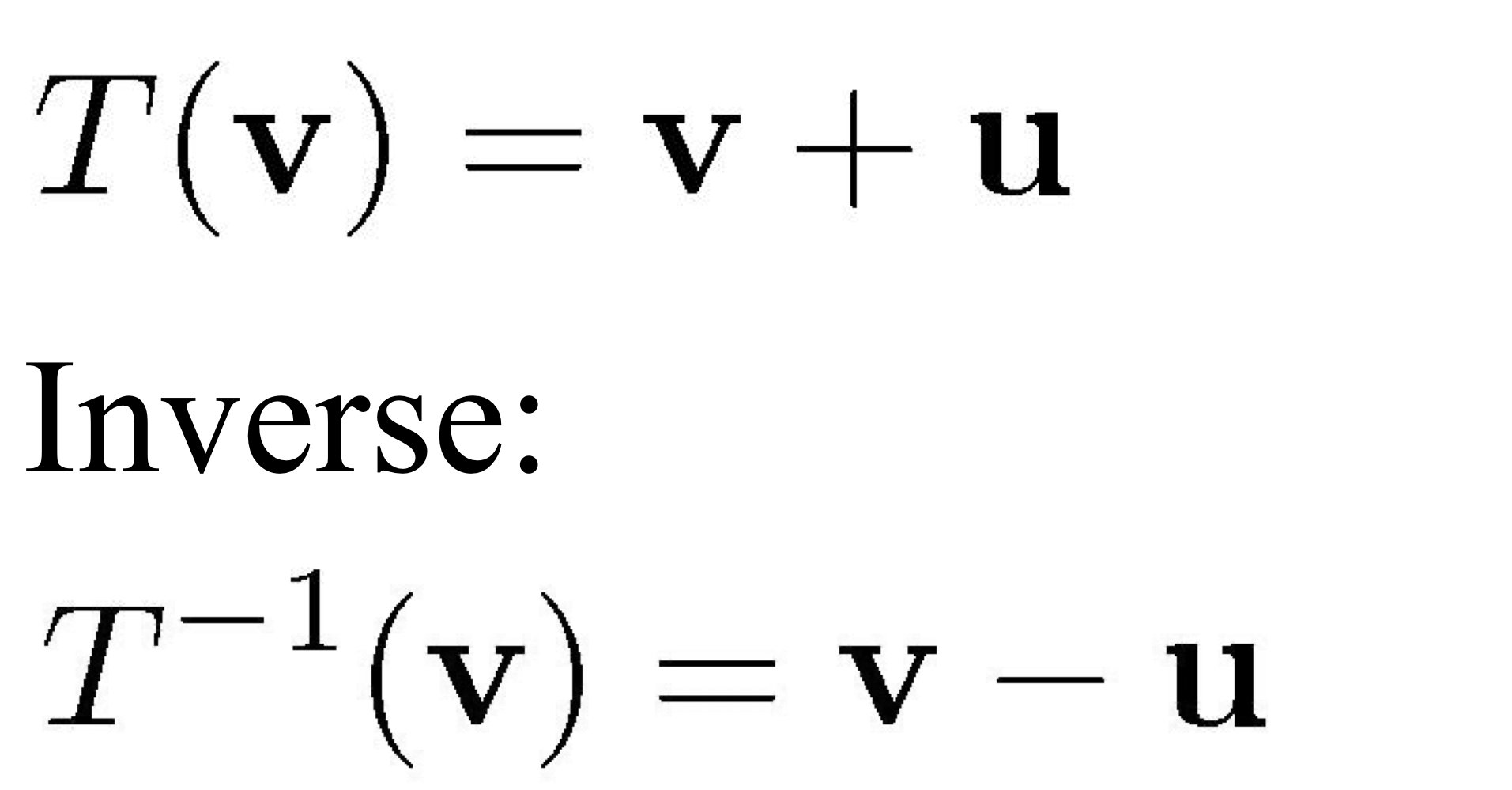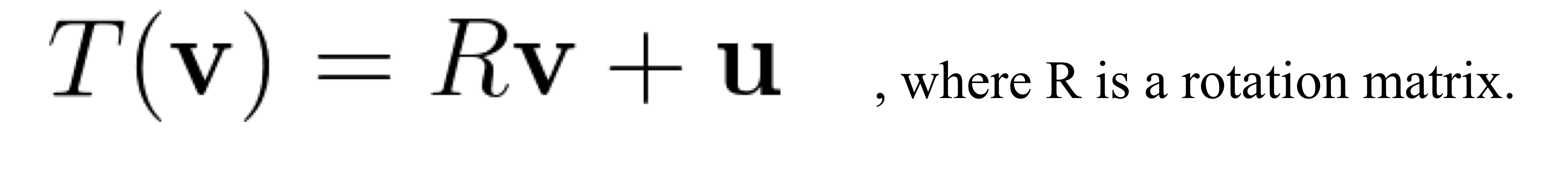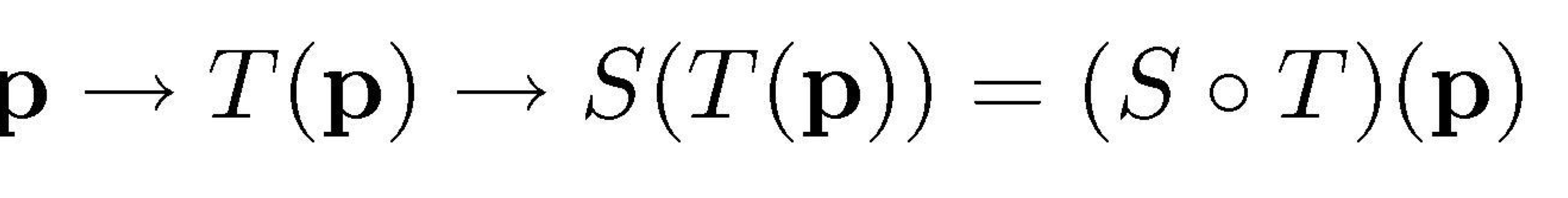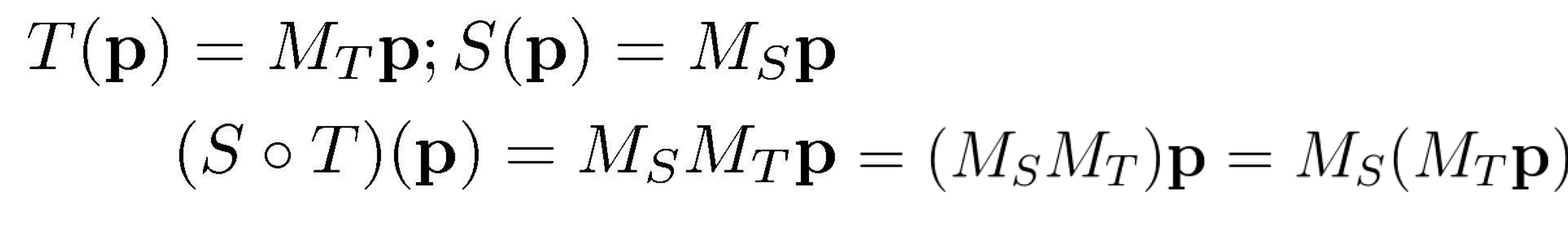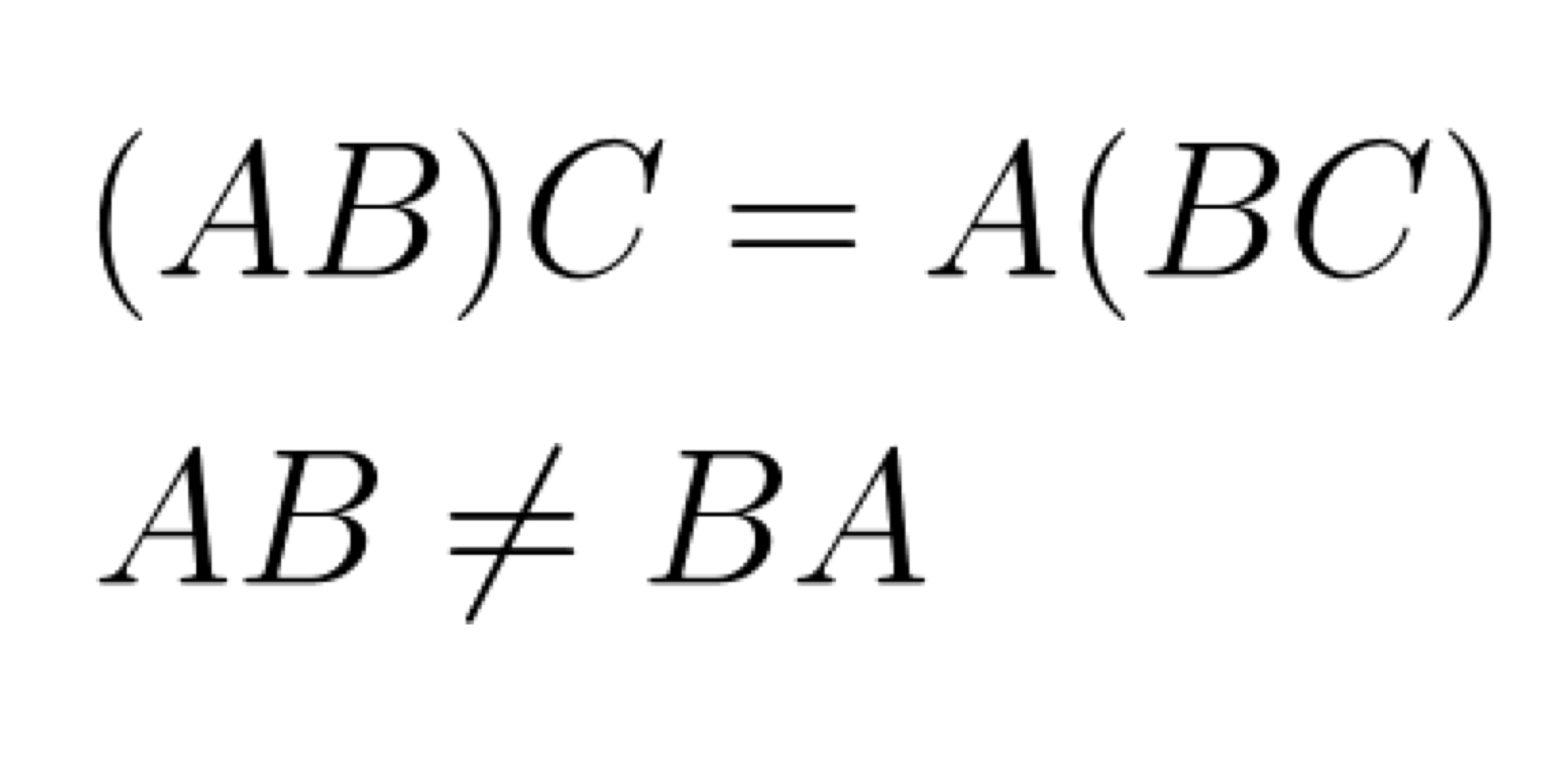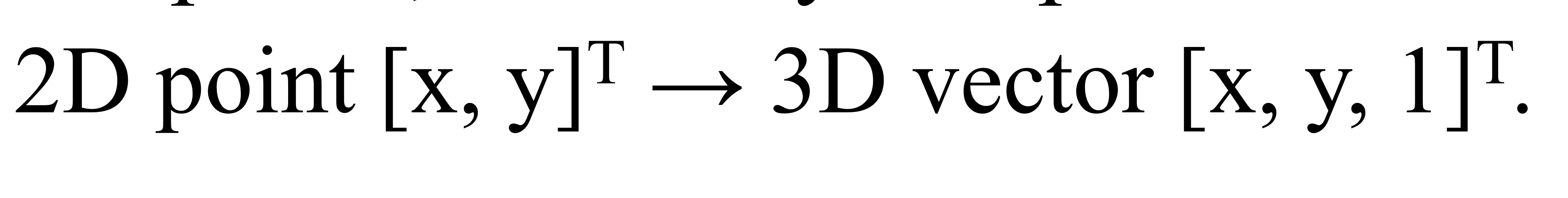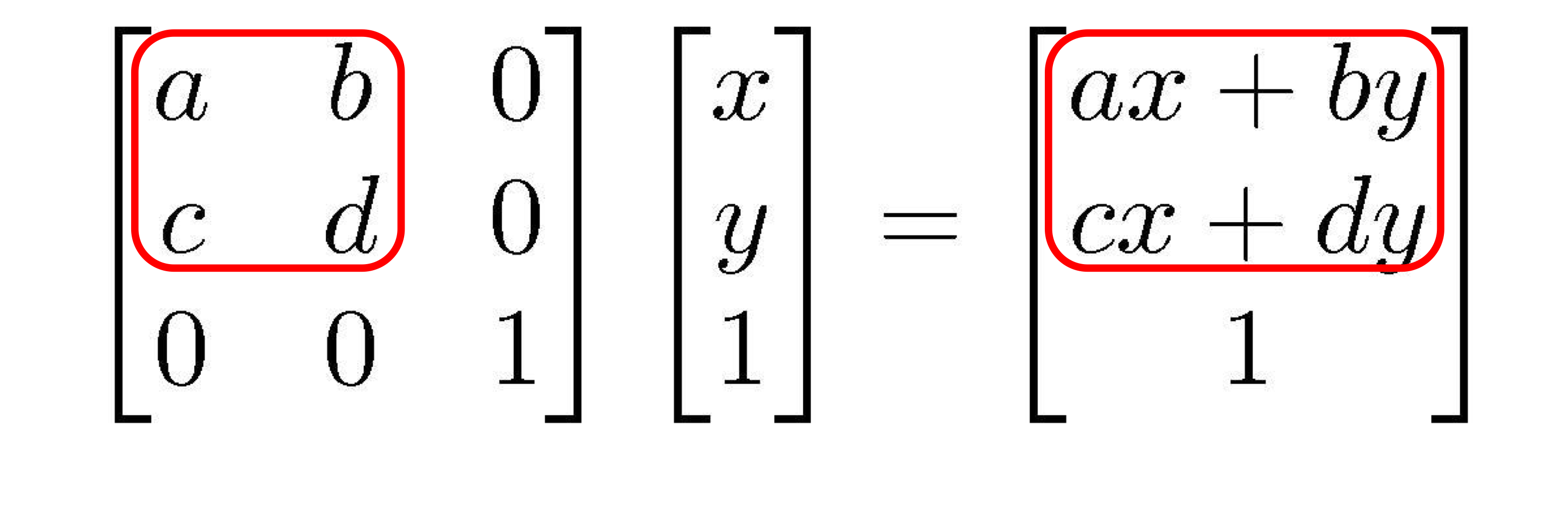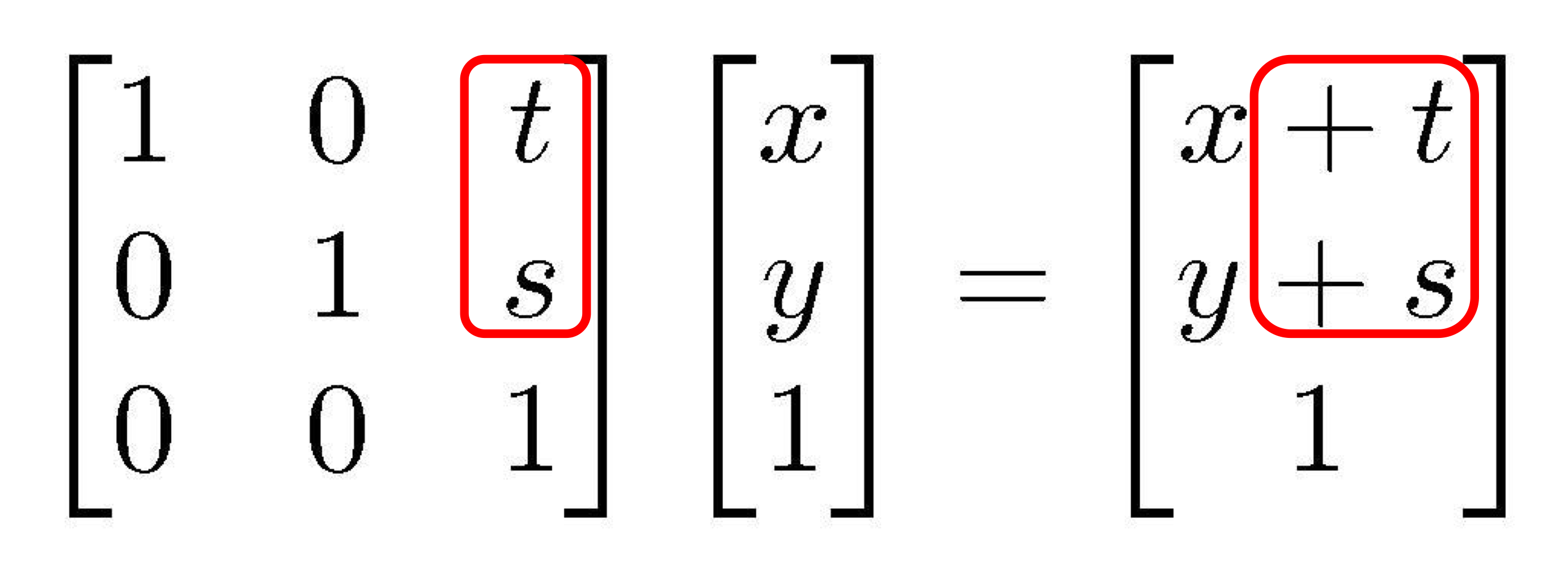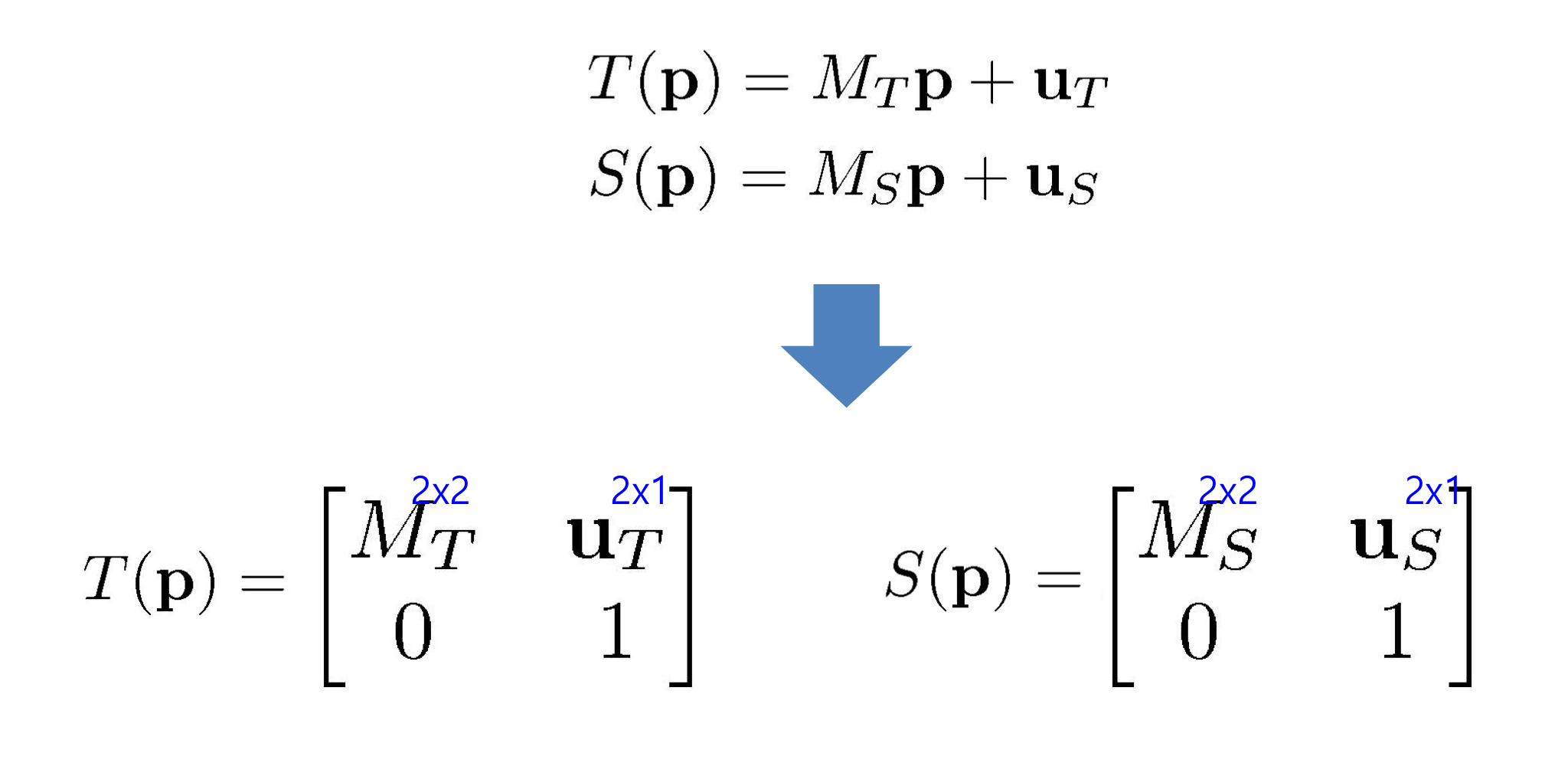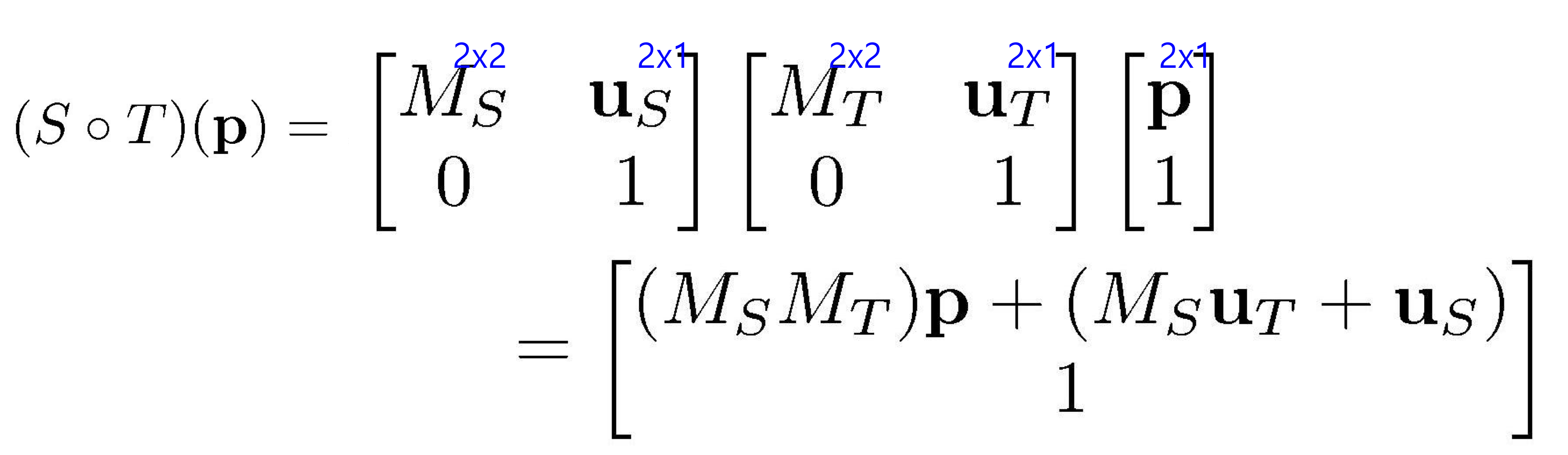2D Transformation
What is Transformation?
- Geometric Transformation- 기하 변환을 의미한다.
- Translate(평행이동), Rotate, Scale, Shear(한쪽으로 미는거), Reflect
Where is Transformation used?
- Movement: 움직임을 표현하기 위해 사용된다.
- Image/object manipulation(조작): 이미지나 물체를 조작하기 위해 사용
- Viewing, projection transformation
: 임의의 3D 가상공간 상의 모습을 2D 모니터에 그려내야하는데 이 과정도 변환을 거친것임.
Linear Transformation
- 행렬의 곱으로 정의할 수 있는 transformation을 linear transforamtion 이라고 한다.
→ 이런식으로 transformation T는 matrix M과의 곱으로 나타낼 수 있으므로 linear transformation
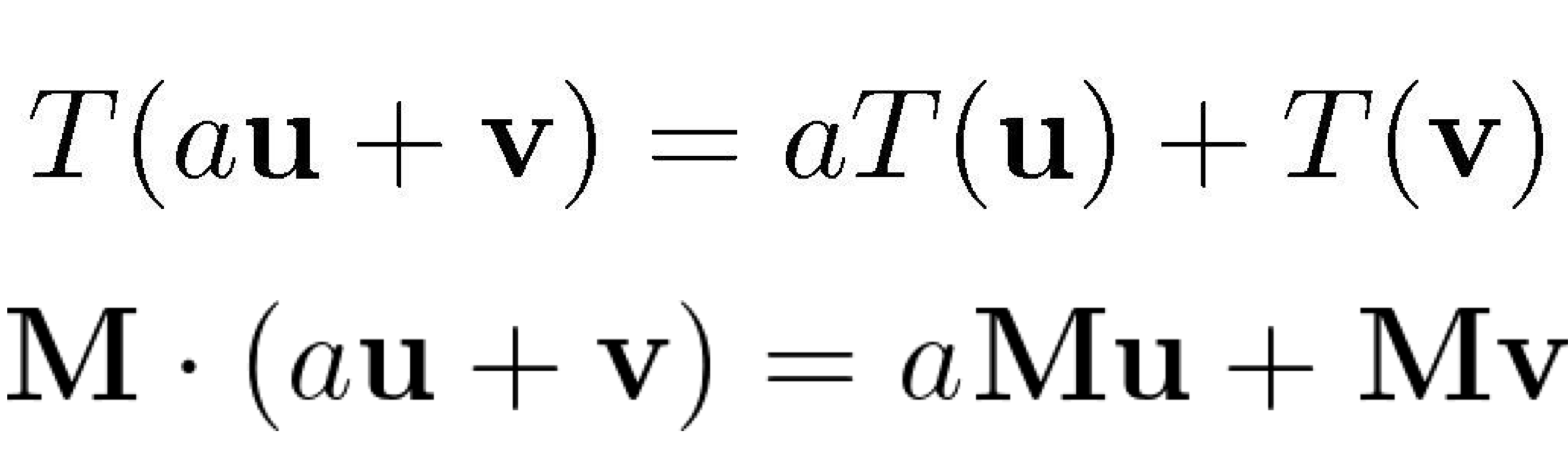
→ ??
2D Linear Transformation
2X2 matrices로 표현할 수 있는 2D linear transformation은?
- uniform scale (고르게 늘리는거)
- non-uniform scale (안고르게 늘리는거)
- rotation
- shear
- reflection
1. Uniform Scale
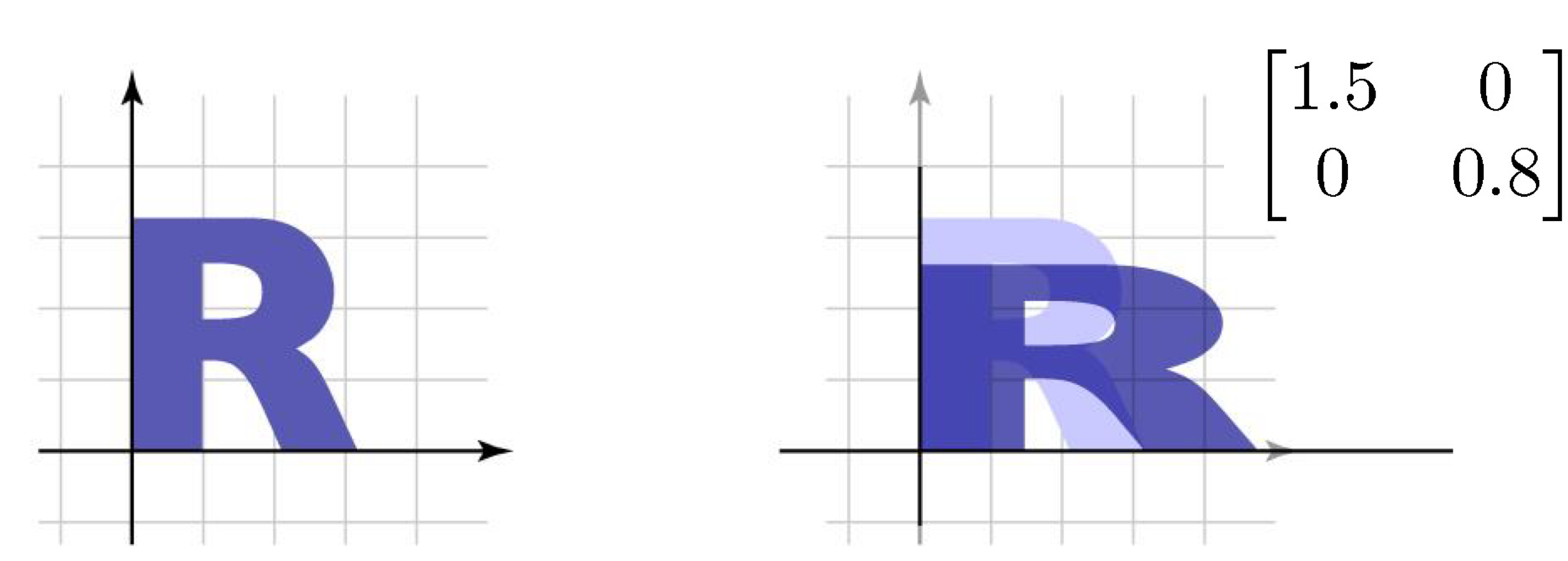
2. Nonuniform Scale
3. Rotation
(1, 0)이 세타만큼 회전하면 (cos세타, sin세타)
(0, 1)이 세타만큼 회전하면 (-sin세타, cos세타)
* 회전에서 양의 방향 = 반시계방향 (CCW rotation)
* rotation 역시 matrix의 곱으로 나타낼 수 있으므로 linear transformation
Numbers in Matrices: Scale, Rotation
matrix 안의 숫자들이 무슨 의미인지 알아보자.
- Scaling
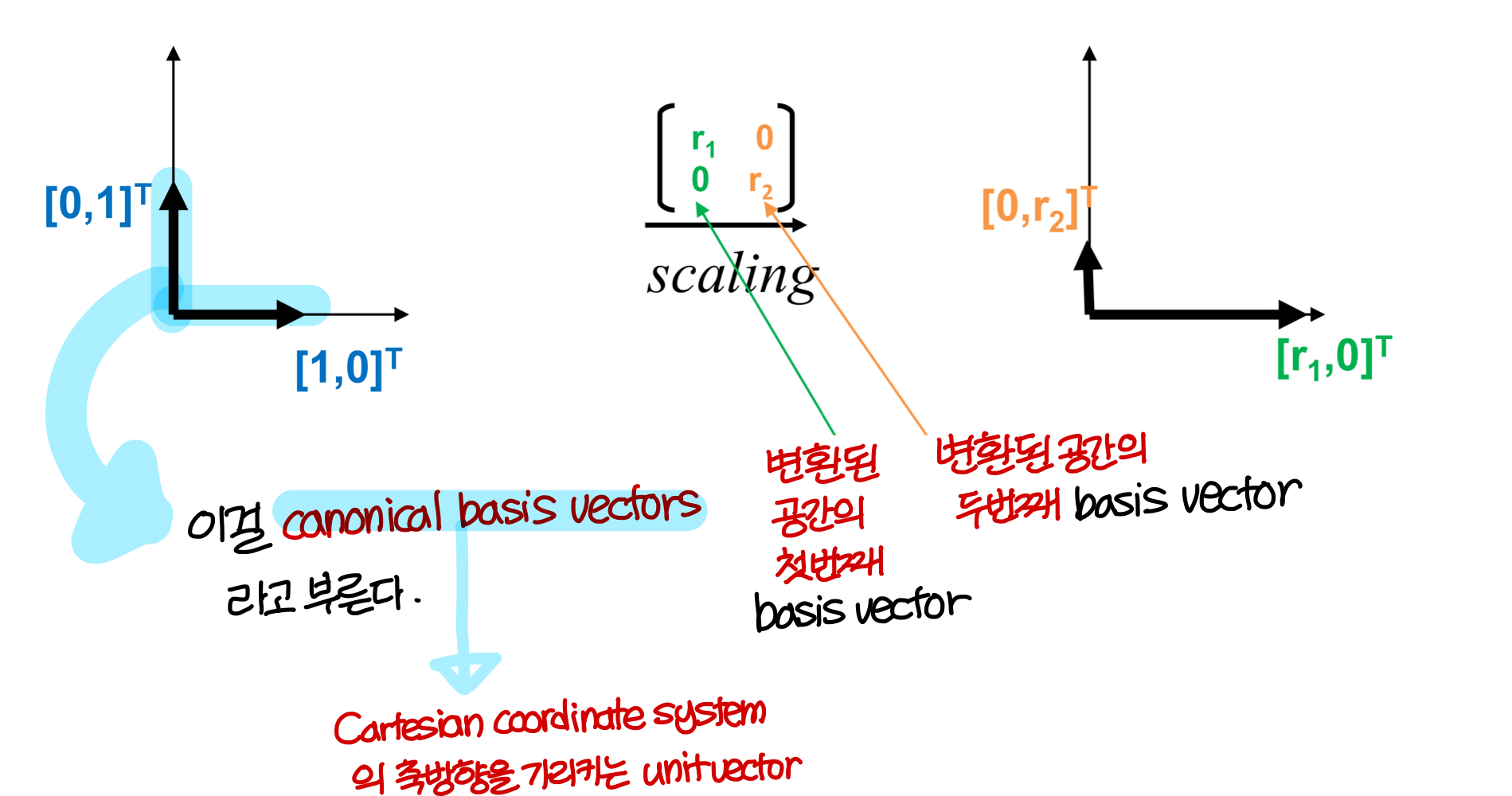
- Rotation
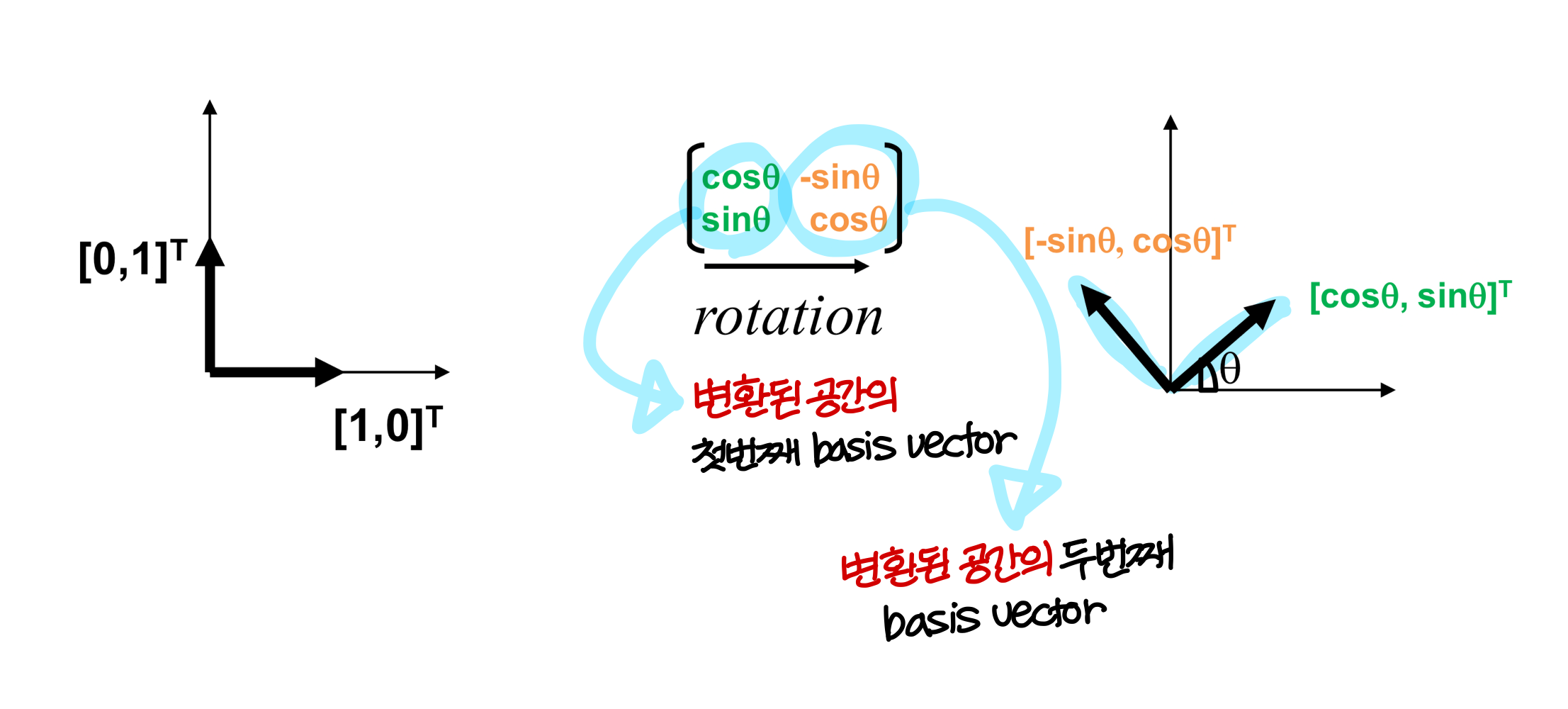
Column space of matrix: column vectors의 linear combination으로 만들 수 있는 span
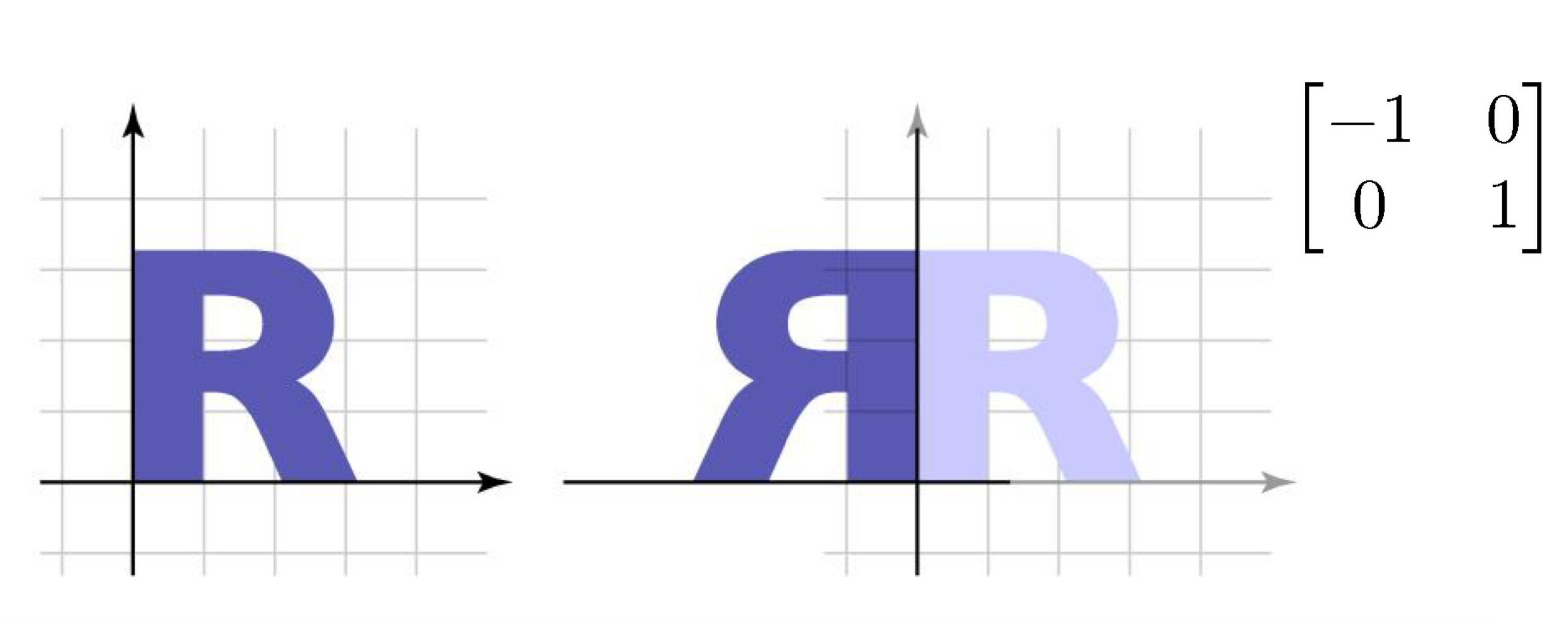
4. Reflection
x축이 (-1, 0)으로 바뀜.
→ y축에 대해 reflection 했다는 의미
non-uniform scale의 특별한 case라 생각해라.
y축이 (a, 1)로 바뀜 → 기울기가 생김
x좌표 값이 x+ay로 바뀌었음
→ y값이 클수록 x값이 더 많이 밀린다는 의미
y좌표 값은 변하지 않음
Shear할 때 축이 바뀐 쪽의 좌표는 변하지 않음
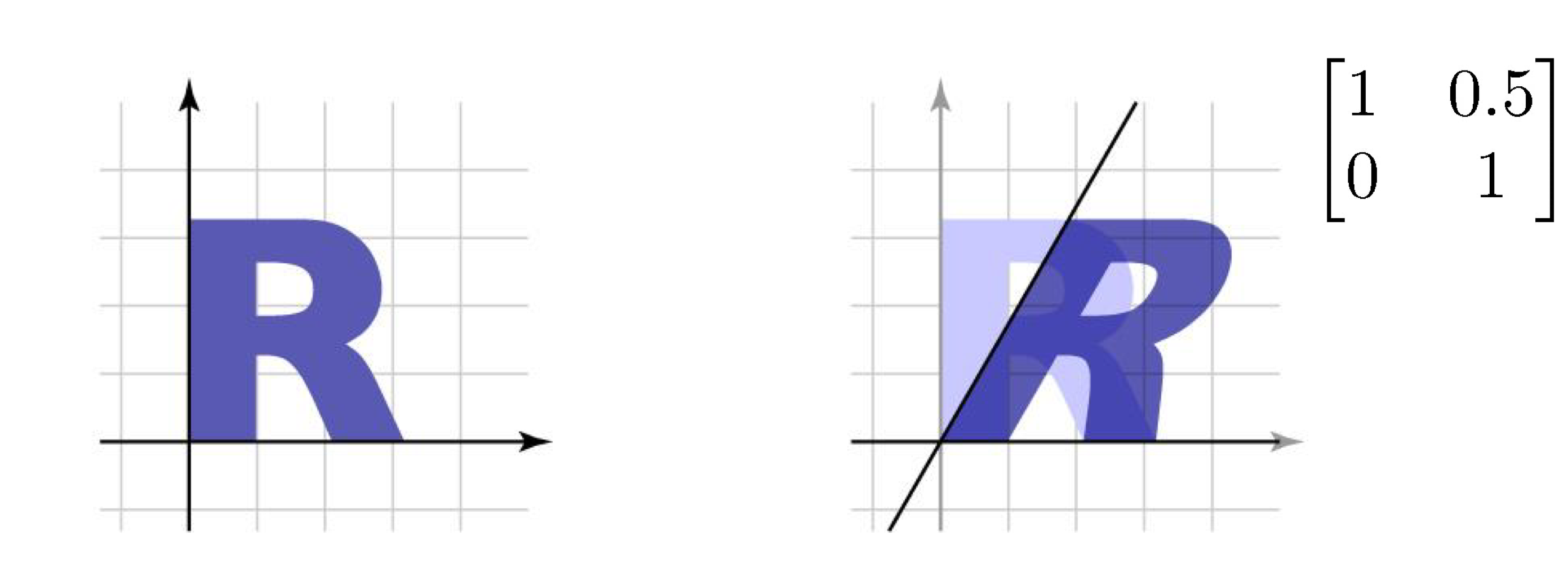
6. Identity Matrix
identity matrix를 곱하면 → 아무것도 안한 상태. 변화가 없다.
축이 (1, 0) (0, 1)로 동일하니까
[Practice] Uniform Scale
import glfw
from OpenGL.GL import *
import numpy as np
def render(M):
glClear(GL_COLOR_BUFFER_BIT)
glLoadIdentity()
#draw coordinate
glBegin(GL_LINES) # GL_LINES는 2개씩 선 끊어서 그린다.
glColor3ub(255, 0, 0). # 빨간색
glVertex2fv(np.array([0., 0.]))
glVertex2fv(np.array([1., 0.]))
glColor3ub(0, 255, 0)
glVertex2fv(np.array([0., 0.]))
glVertex2fv(np.array([0., 1.]))
glEnd()
#삼각형을 그릴건데 (0, 0.5) (0, 0) (0.5, 0)
#이 세 꼭짓점으로 이루어진 삼각형에 matrix M을 곱해 변환할거다
glBegin(GL_TRIANGLES)
glColor3ub(255, 255, 255). # 색깔 다 255이면 흰색임
glVertex2fv(M @ np.array([0.,0.5]))
glVertex2fv(M @ np.array([0.,0.]))
glVertex2fv(M @ np.array([0.5, 0.]))
glEnd()
def main():
#glfw 써서 window 만들어야하는데 glfw가 init되지 않았다면 곤란..
if not glfw.init():
return
#glfw init된거 확인했으니 window create
window = glfw.create_window(640, 640, "2D TRANS", None, None)
#window 정말 만들었는지 확인
if not window:
glfw.terminate()
return
#window 만들어진거 확인했으니 띄우기
glfw.make_context_current(window)
while not glfw.window_should_close(window):
#Poll events (이 함수에서 무슨 이벤트인지 검사하고 무슨일 할지 콜백함수로 호출)
glfw.poll_events()
M = np.array([[2., 0.], [0., 2.]]) # x축 y축 방향으로 2배씩 늘리는 matrix
#Render here, e.g. using pyOpenGL (화면에 그린다. 렌더링)
render(M)
# Swap front and back buffers
#(back에서 위와 같은 일이 일어나면 front(우리가 보는 화면)에 반영한다.)
glfw.swap_buffers(window)
glfw.terminate()
if __name__ == "__main__"
main()glBegin(GL_LINES)
→ 이거 2개씩 끊어서 선 그린다. glVertex로 점 a, b, c, d 입력해주면 a-b , c-d 이렇게 선 2개 그림
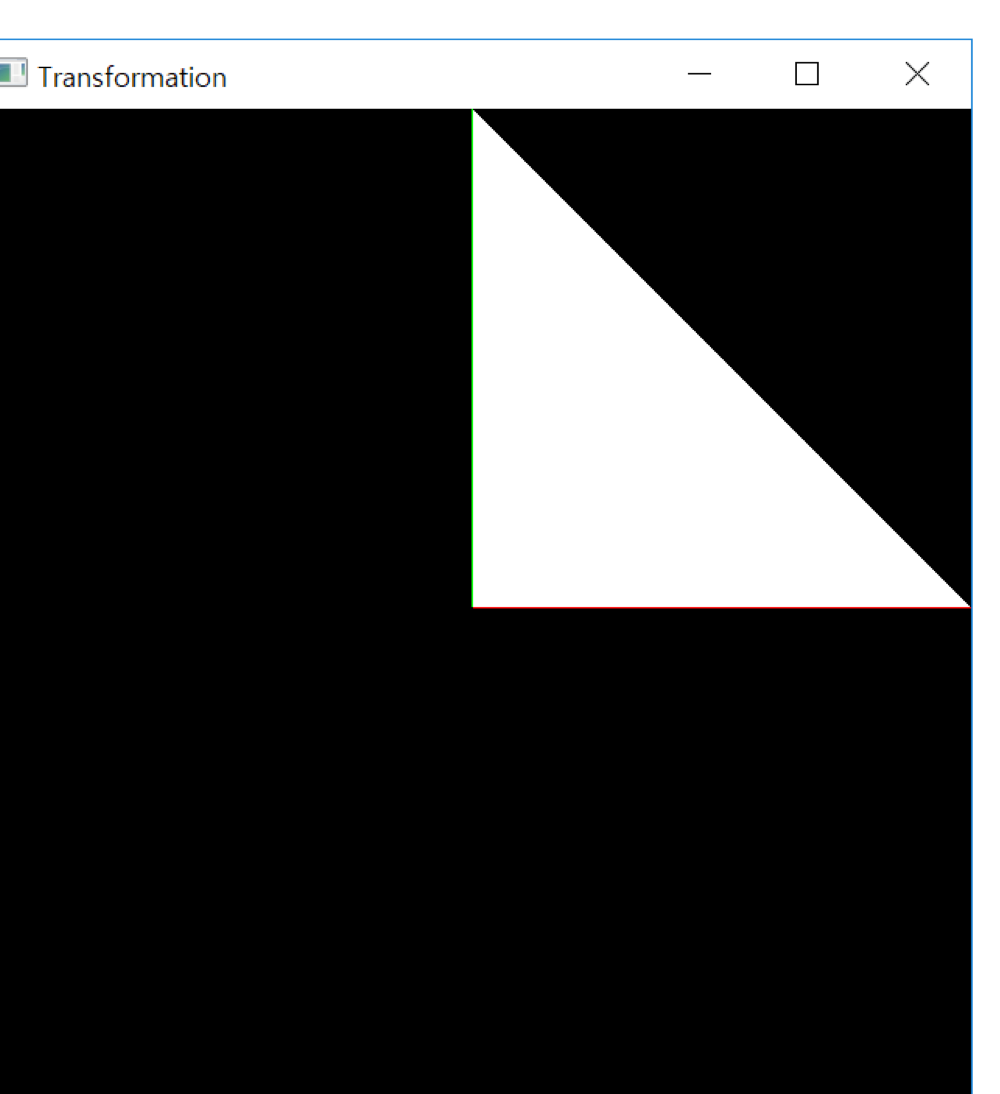
(0.0) (0.5, 0) (0, 0.5)이 꼭짓점인 삼각형을 x축 방향 y축 방향으로 각각 2배씩 늘렸으니 왼쪽과 같이 된다.
[Practice] Animate It!
매번 스케일링 벡터를 다르게 하면 애니메이션이 된다.
glfw.swap_interval(1) #이거 넣어줘야한다!! 안넣어주면 삼각형이 엄청 빠르게 돈다.
while not glfw.window_shoud_close(window):
glfw.poll_events()
#현재 시간을 seconds로 받아온다.
t = glfw.get_time()
s = np.sin(t)
M = np.array([[s, 0.], [0, s]])
render(M)
glfw.swap_buffers(window)
glfw.terminate()glfw.swap_interval(1)
→ glfw.swap_buffer()를 calling하기 전에 스크린 refresh를 몇번할지 set해주는거 (하드웨어 레벨의 이야기)
(이렇게 1로 set안하면 제한없이 막 refresh 해서 삼각형 엄청 빠르게 움직인다.
→ 만약 모니터의 refresh rate가 60Hz면 while loop는 1/60 초마다 반복된다.
위의 코드로 uniform scale 의 render 함수를 돌리면 삼각형이 커졌다 작아졌다 한다.
#nonuniform scale
t = glfw.get_time()
s = np.sin(t)
M = np.array([[s, 0.], [0., s*.5]])
render(M) #shear
t = glfw.get_time()
a = np.sin(t)
M = np.array([[1., a], [0., 1.]])
render(M)
y축이 (-1, 1)과 (1, 1) 사이에서 움직인다.
x 좌표값은 변하지 않는다.
그치만 가로로 봤을때 걸리는건 x쪽이니까 = x축 방향으로 민다는거
Quiz #1
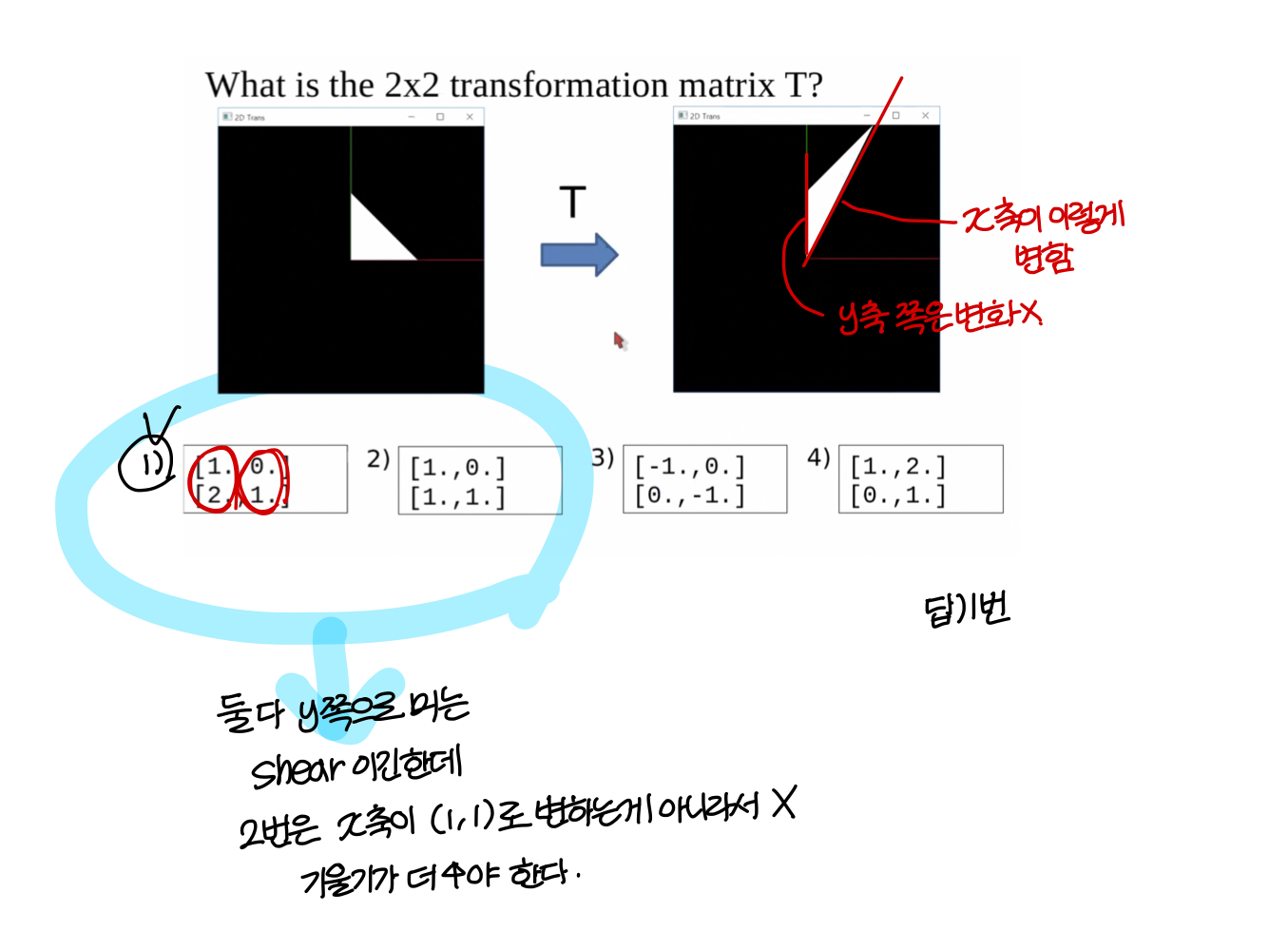
2D Translation
병진운동 다음과 같이 표현할 수 있다.
🥵주의! Translation은 matrix의 곱으로 표현 불가
벡터의 합으로 표현할 수 있다. (왼쪽처럼)
즉, linear transformation이 아니다.
😀 linear transformation과 Translation을 합쳐서 표현하면
T(v) = Mv + u
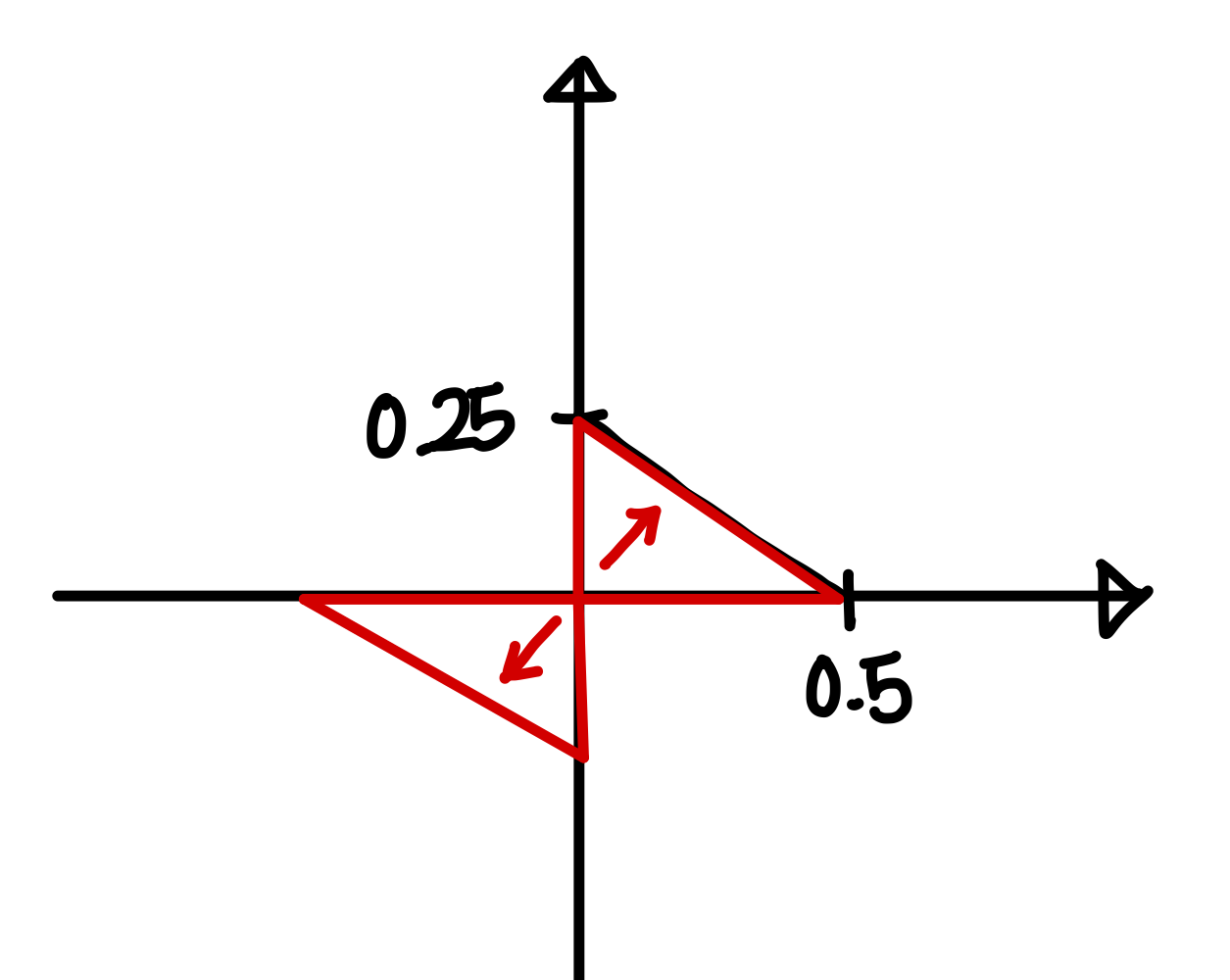
[Practice] Translation
def render(u): # u 받아온다.
glBegin(GL_TRIANGLES)
glColor3ub(255, 255, 255) #흰색
glVertex2fv(np.array([0.0, 0.5]) + u)
glVertex2fv(np.array([0.0, 0.0]) + u)
glVertex2fv(np.array([0.5, 0.0]) + u)
glEnd()
def main():
~~~
while not glfw.window_shoud_close(window):
glfw.poll_events()
t = glfw.get_time()
u = np.array(np.sin(t), 0.])
render(u)예상결과) render의 argument로 [-1 ~ 1, 0]이 넘어간다.
(0, 0) (0, 0.5) (0.5, 0)이 꼭짓점인 삼각형이 x축방향으로 -1~1만큼 왔다갔다 함
sin 그래서 기울기는 값이 1, -1 근처일때 완만함. 그래서 끝부분에서 움직일 때 삼각형의 속도가 느려짐
Check again
- Linear transformation
종류: Scale, rotation, reflection, shear
matrix의 곱으로 표현된다.
- Translation
matrix의 곱으로 표현안된다.
vector addition을 통해 표현할 수 있다.
- Affine Transformation
정의) Linear transformation + Translation
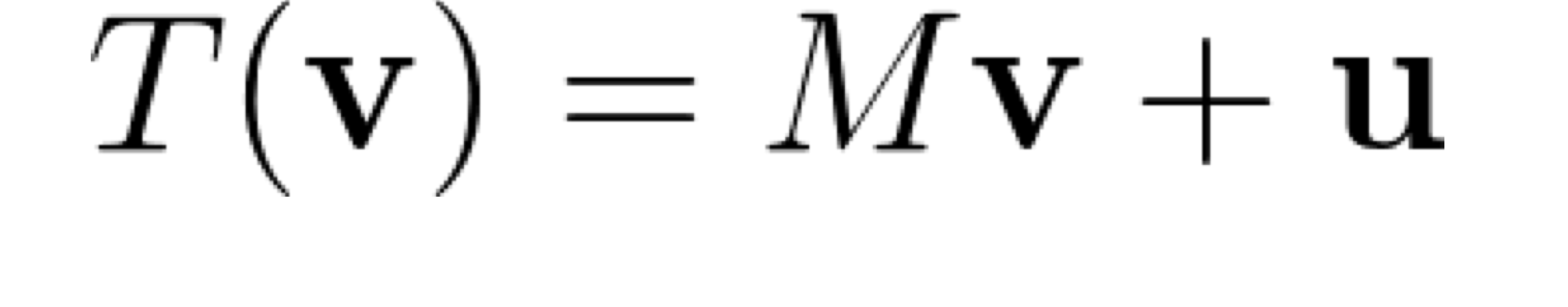
- Preserve lines : line을 affine transformation 해도 line이다.
- Preserves parallel lines: 두 line이 평행하면 변형하더라도 평행
- Preserves ratios of distance: 변형하더라도 line 사이의 거리 비율은 유지
→ 이 성질은 linear transformation으로부터 물려받은거
(linear transformation이 이 성질을 만족. translation은 모양 그대로 유지해줌.
그래서 Affine Transformation도 이 성질을 만족)
Rigid Transformation
Rotation + Translation
- Rigid Transformation은 앞에서 본 affine transformation 성질 모두 만족(한 종류이므로)
그 성질에다가 아래 두 성질을 추가적으로 만족
- 모든 점들 간 사이의 거리 유지 (rotation과 translation 모두 모양을 바꾸진 않는다.)
- 모든 벡터의 cross product를 유지한다. (부호까지. 즉, reflection이 되지 않는다는 말임. reflection되면 부호 반대.)
[Practice] Affine Translation
def render(M, u):
glBegin(GL_TRIANGLES)
glColor3ub(255, 255, 255)
glVertex2fv(M @ np.array([0.0, 0.5]) + u)
glVertex2fv(M @ np.array([0.0, 0.0]) + u)
glVertex2fv(M @ np.array([0.5, 0.0]) + u)
glEnd()
def main():
#...
while not glfw.window_should_close(window):
glfw.poll_events()
t = glfw.get_time()
th = t
R = np.array([[np.cos(th), -np.sin(th)],
[np.sin(th), np.cos(th)]])
u = np.array([np.sin(t), 0.])
render(R, u)
#...결과) 실시간으로 시계 반대방향으로 회전하면서 -1 ~ 1만큼 x 축방향으로 움직이는 삼각형
Quiz #2

Composing Transformations & Homogeneous Coordinates
Order Matters!
Matrix multiplication은 associative 하지만 commutative 하지 않다는걸 기억해라
[Practice] Composition
def main():
~~~
while not glfw.window_should_close(window):
glfw.poll_events()
S = np.array([[1., 0.], [0., 2.]])
th = np.radians(60)
R = np.array([[np.cos(th), -np.sin(th)],
[np.cos(th), np.cos(th)]])
u = np.zeros(2)
render(R @ S, u) #-> 이거 하면 x축으로 1배 y축으로 2배 늘리고 회전시킨다.
#render(S @ R, u) -> 이거하면 회전시키고 x축으로 1배 y축으로 2배 늘린다. 직각이 무너진다. Problems when handling Translation as Vector Addition
translation을 matrix 곱으로 표현못한다고 해서 벡터의 합으로 다루게 된다면
→ linear transformation과 translation을 일관되게 다루지 못한다.
→ affine transformation을 composing 하는게 복잡해짐.
Homogeneous Coordinates
- Key idea: 2D points를 3D coordinate space에 표현하기
- Affine transformation은 다음과 같이 표현한다.
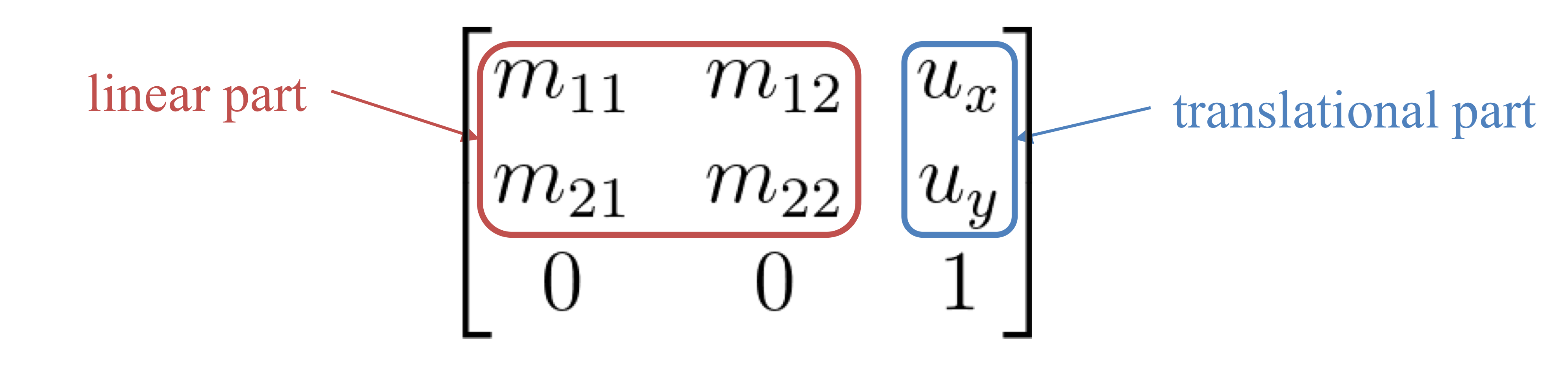
😀 주의해야함. 위의 matrix가 의미하는건 lienar transformation 먼저하고 translation 하는거
lienar matrix를 M이라하고 translation matrix를 T라 할 때 위 matrix는 T*M
- Homogeneous Coordinates를 사용해서 affine transformation을 처리하면 훨씬 깔끔하다.
[Practice] Homogeneous Coordinates
def render(M) #이번엔 3X3 matrix
~~~
glBegin(GL_TRIANGLES)
glColor3ub(255, 255, 255)
glVertex2fv((M @ np.array([.0, .5, 1.]))[:-1]) # 계산시에 점에 w = 1 요소 더하기
# 그러고 결과에서 맨 뒤에껄 빼는거임
glVertex2fv((M @ np.array([.0, .0, 1.]))[:-1])
glVertex2fv((M @ np.array([.5, .0, 1.]))[:-1])
glEnd()
def main():
~~~
while not glfw.window_shoud_close(window):
glfw.poll_events()
# rotate 60 deg about z axis
th = np.radians(60)
R = np.array([[np.cos(th), -np.sin(th), 0.],
[np.sin(th), np.cos(th), 0.],
[0., 0., 1.]])
# translate by (.4, .1)
T = np.array([[1., 0., 4],
[0., 1., 1],
[0., 0., 1]])
render(R) # p'= Rp (60도 회전)
#render(T) (0.4, 0.1)만큼 평행이동
#render(T @ R) p'= TRp 60도 회전하고 (0.4, 0.1만큼 평행이동)
#render(R @ T) p'= RTp (0.4, 0.1)만큼 이동하고 60도 회전
# [[np.cos(th), -np.sin(th), 4]
# [np.sin(th), np.cos(th), 1.]
# 0, 0, 1]] -> 이거는 p'= TRp Summary: Homogeneous Coordinates 2D
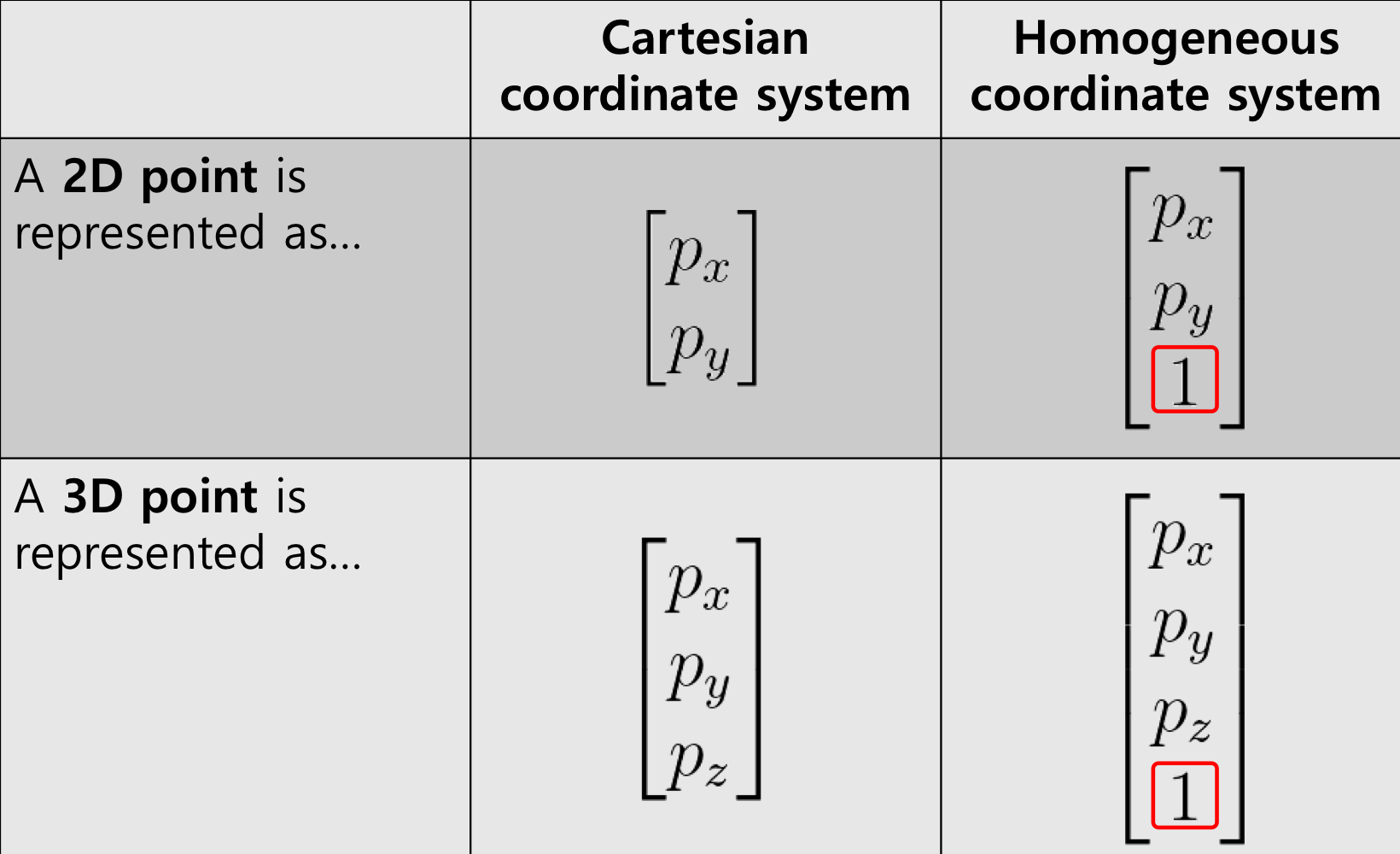
- 2D point를 위해 (x, y, 1) ^T 를 (x, y)^T 대신 사용한다. (Transpose 주의)
- 2D linear transformation을 위해 3x3 matrices를 2x2 matrices 대신 사용한다.
- 2D translation을 위해 3x3 matrices를 벡터 덧셈 대신 사용한다.
→ linear transformation과 translation을 consistent manner로 다룰 수 있음.
- Homogeneous Coordinate를 3차원에서도 사용할 수 있다. (4x4 행렬 사용)
Quiz #3

3D Cartesian Coordinate System
지금까지 다룬건 2D world. 이제 3D를 다루자!!
coordinate system 뜻) 좌표계
cartesian coordinate system 뜻) 직교 좌표계: 좌표 축들끼리 직교하는거
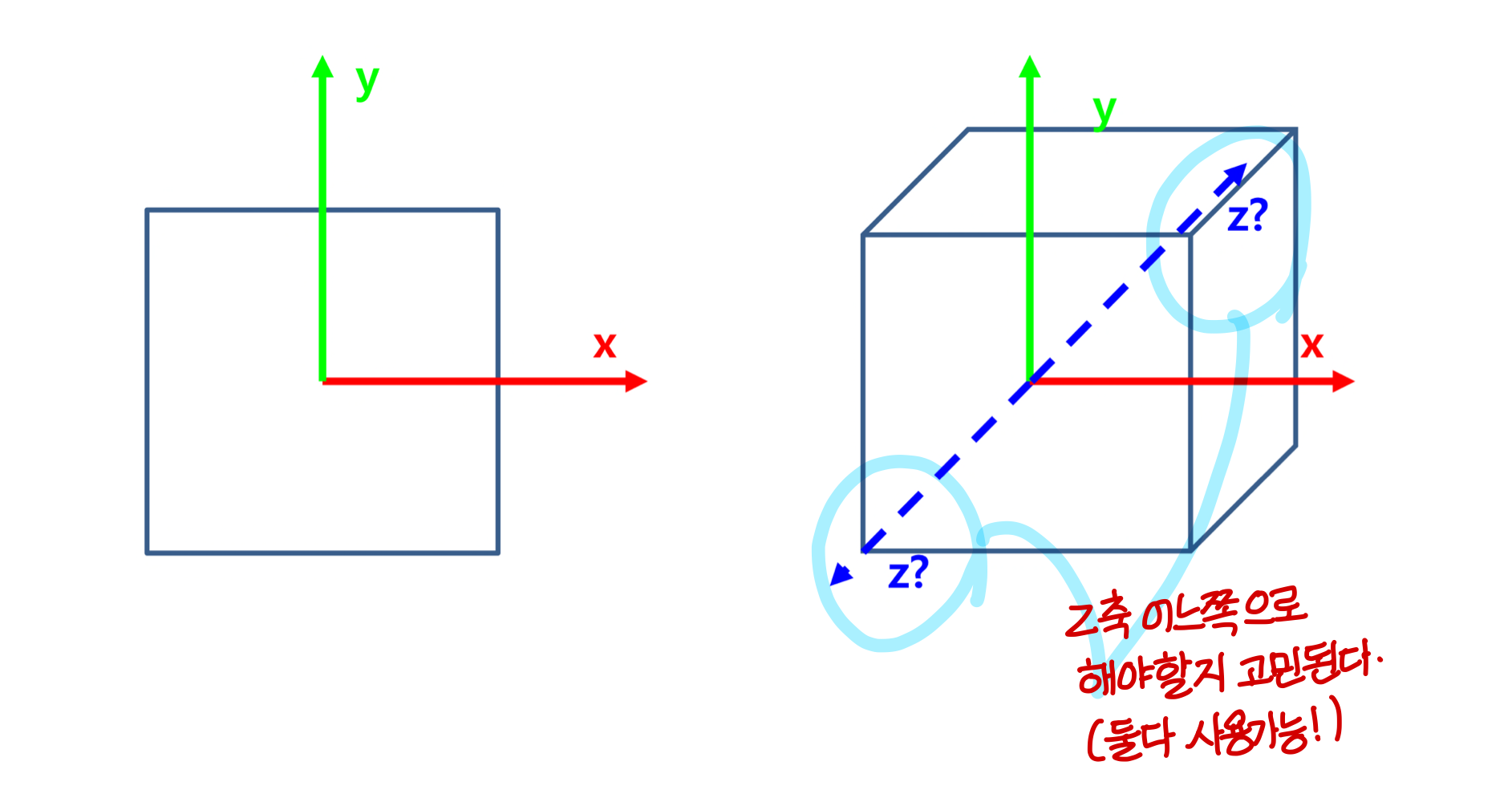
Two Types of 3D Cartesian Coordinate Systems (z축 방향에 따라)
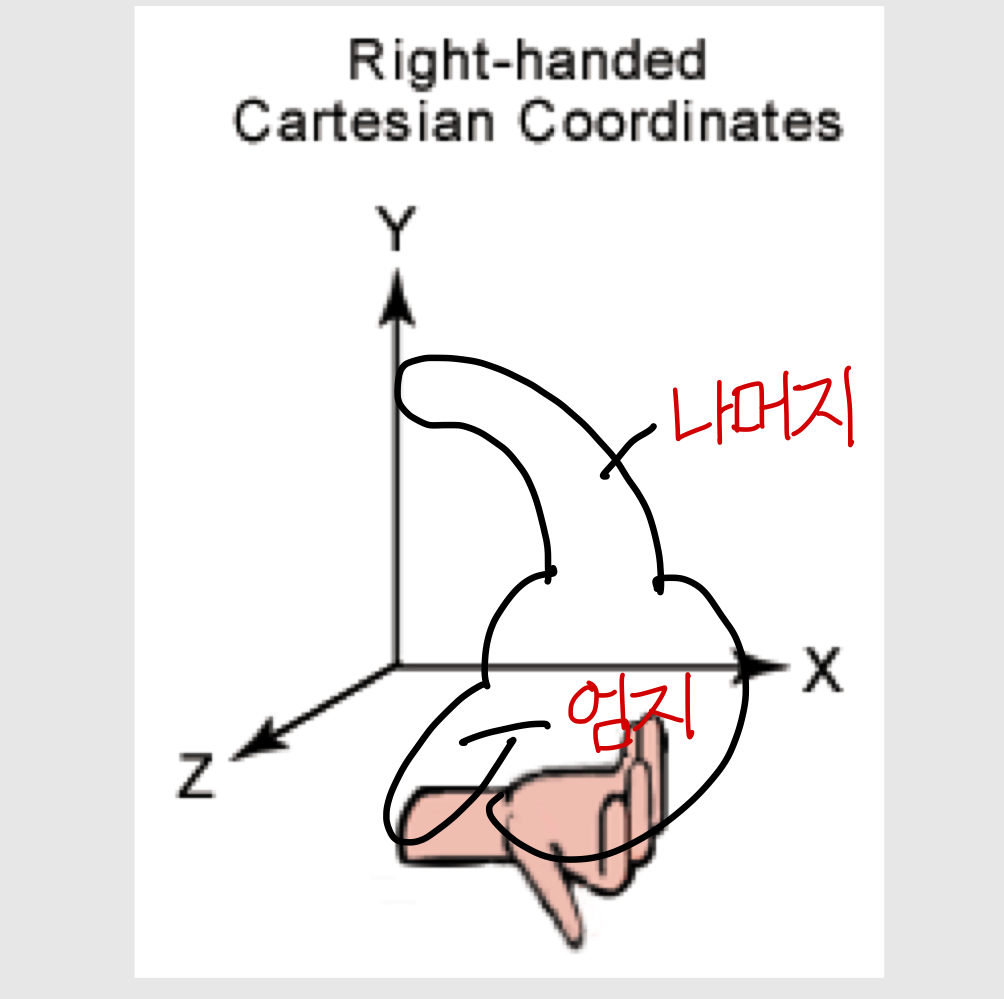
- Right-handed Cartesian Coordinates (우리가 사용하는거)
- 특정 축을 기준으로 회전할 때 축의 양의 방향으로 오른손의 엄지를 가리키고 나머지 손이 휘감는 방향이 양의 회전방향
→ (이렇게 되면 특정 축의 화살표를 맞는 방향으로 섰을 때 반시계 방향이 양의 방향임)

- OpenGL, AutoCad, Standard for Physics & Math
- 특정 축을 기준으로 회전할 때 축의 양의 방향으로 오른손의 엄지를 가리키고 나머지 손이 휘감는 방향이 양의 회전방향
- Left-handed Cartesian Coordinates
위에서 했던걸 왼손으로 하면 된다. Unity에서 표준임.
Point Representation in Cartesian & Homogeneous Coordinate System
Uploaded by N2T