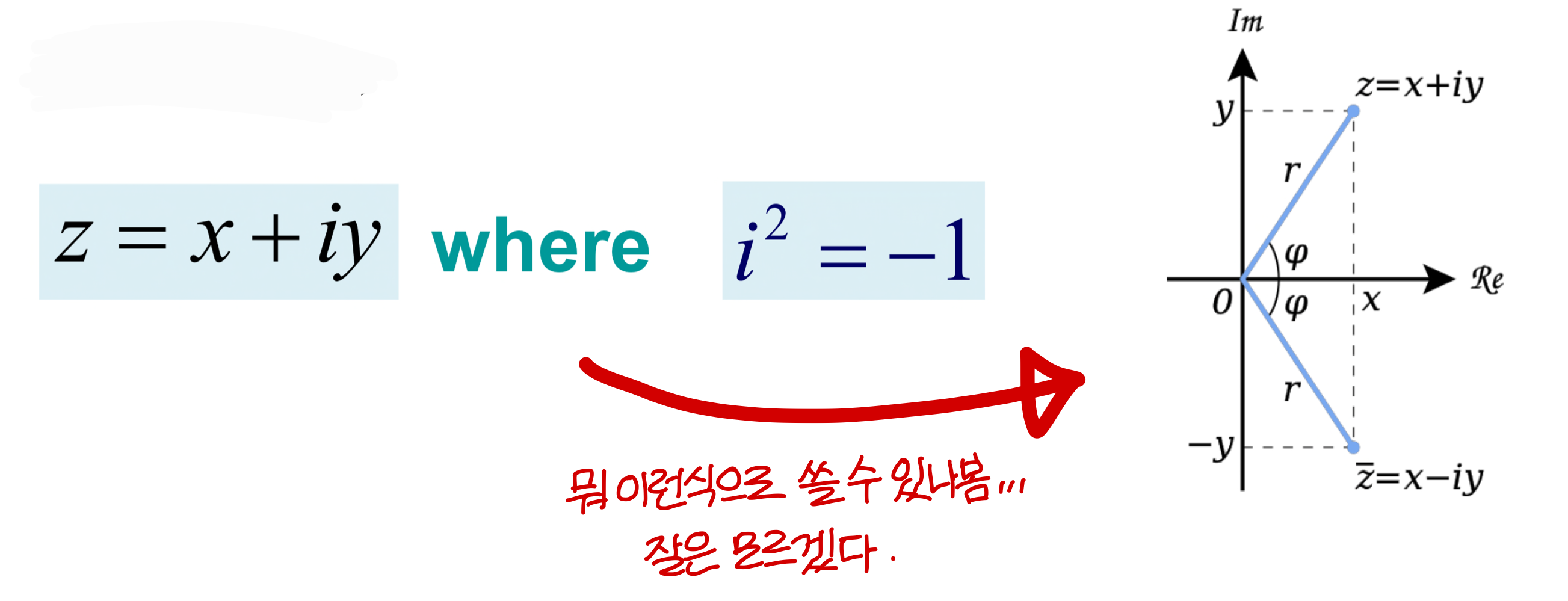
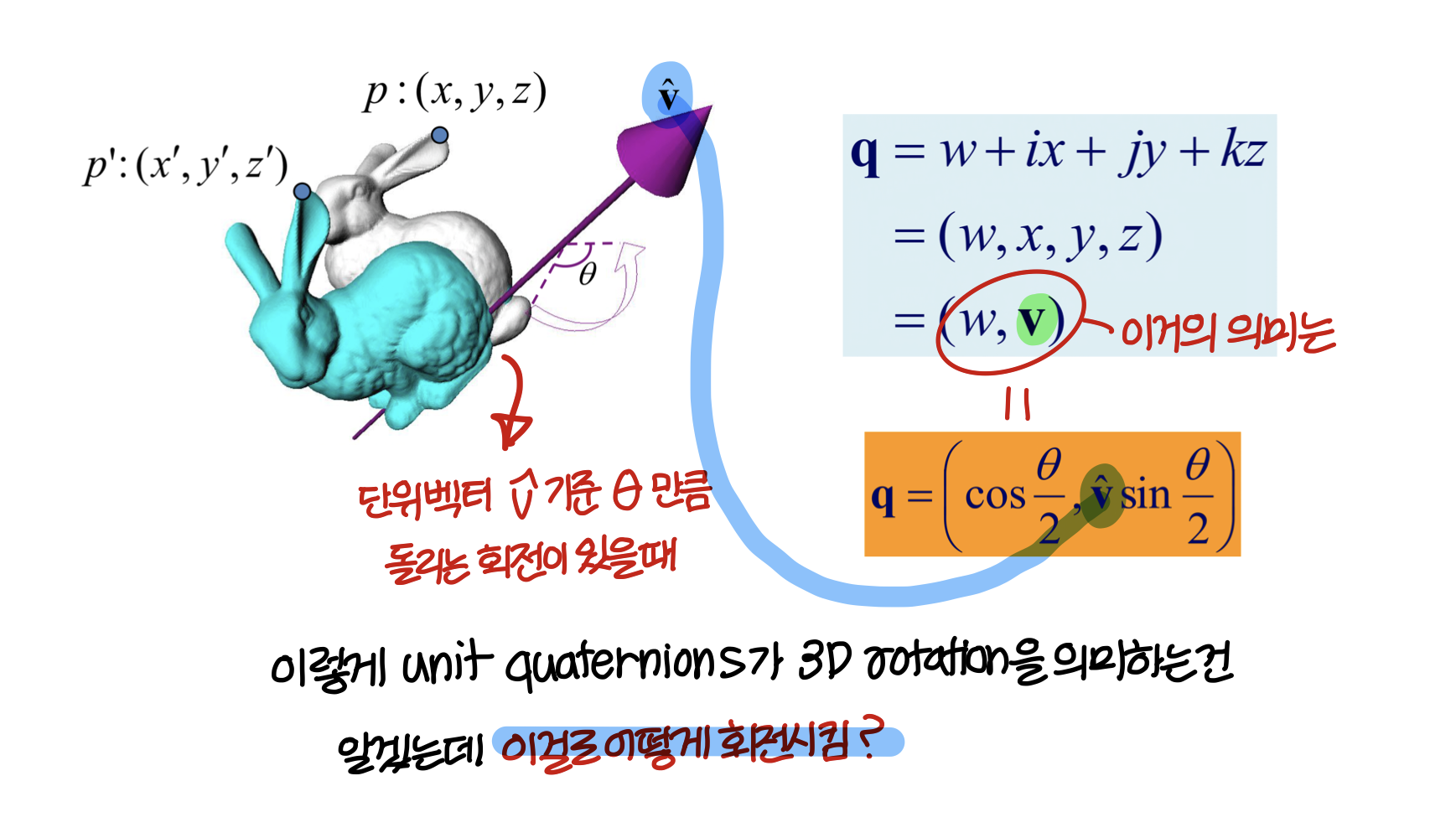
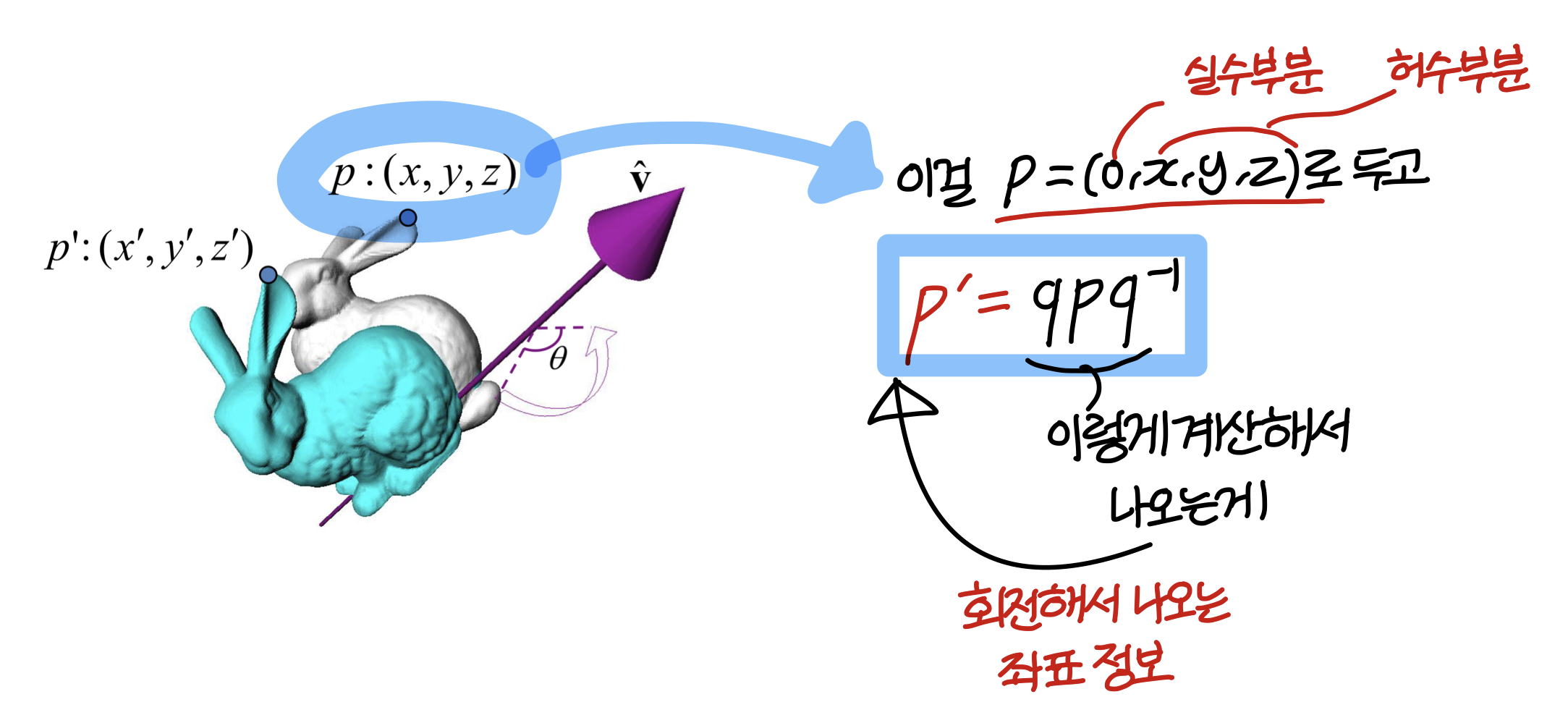
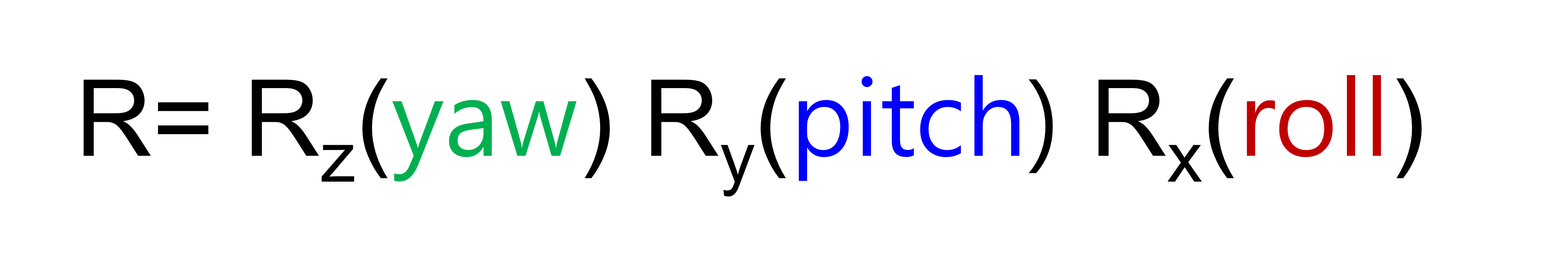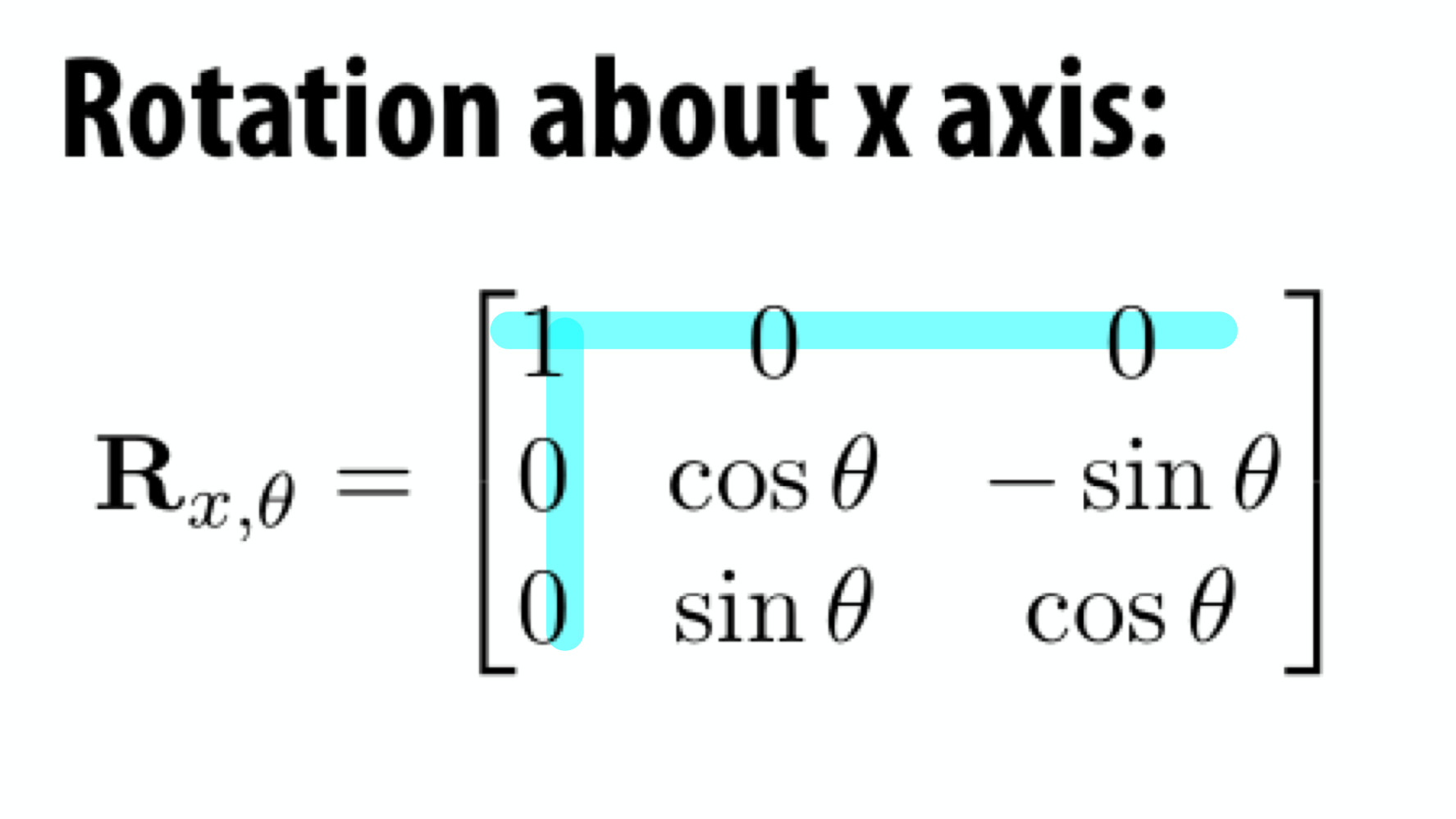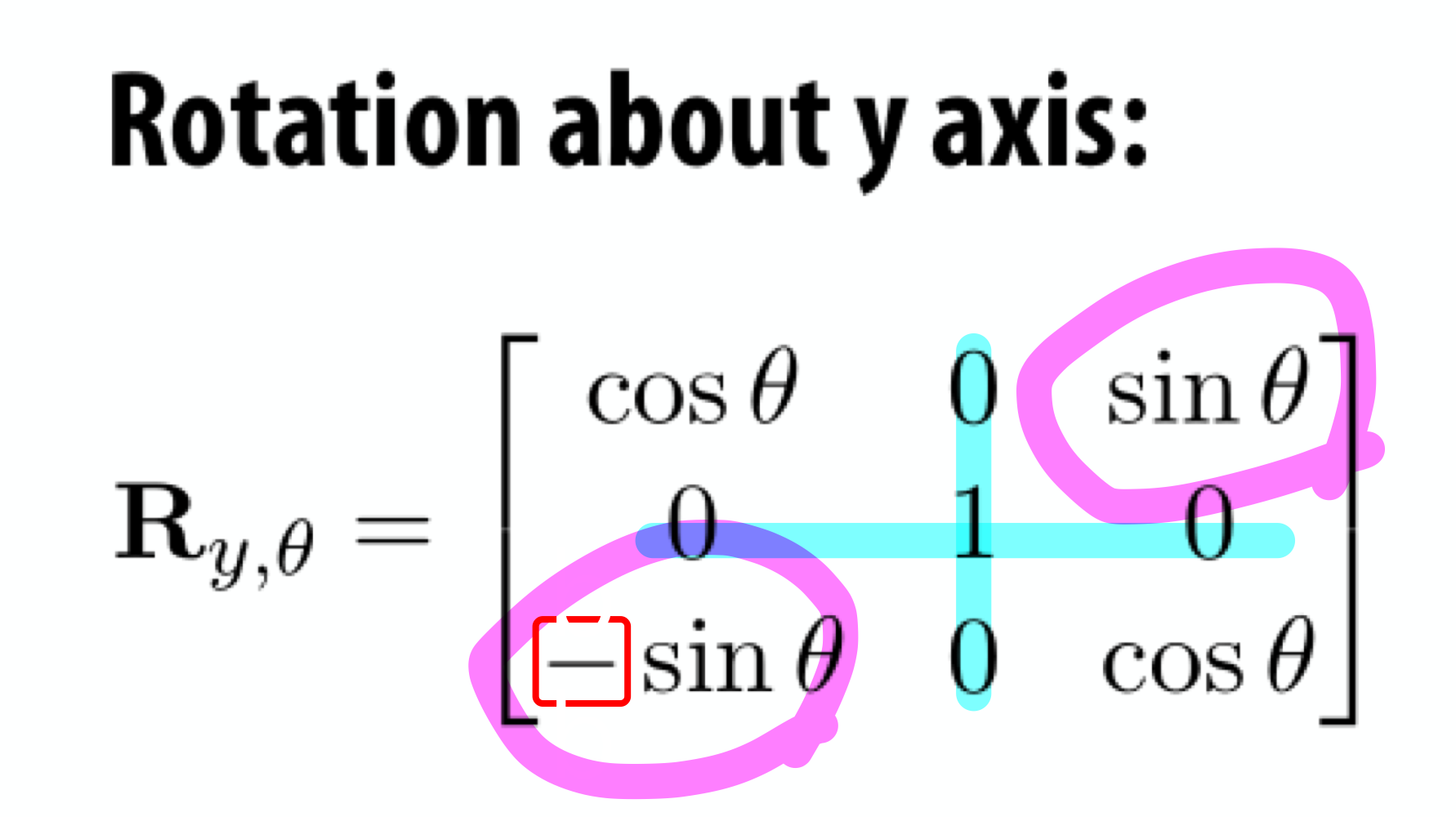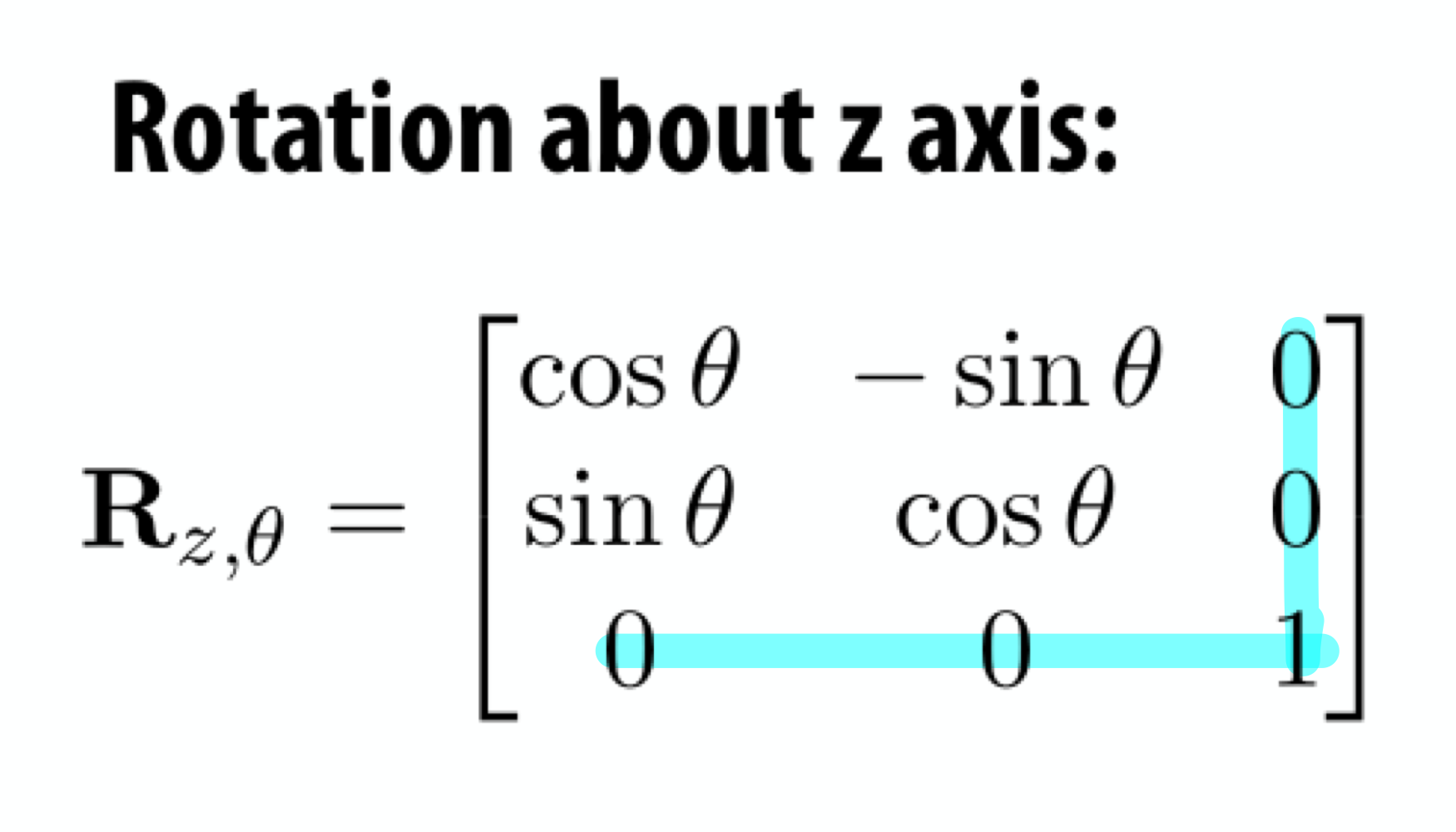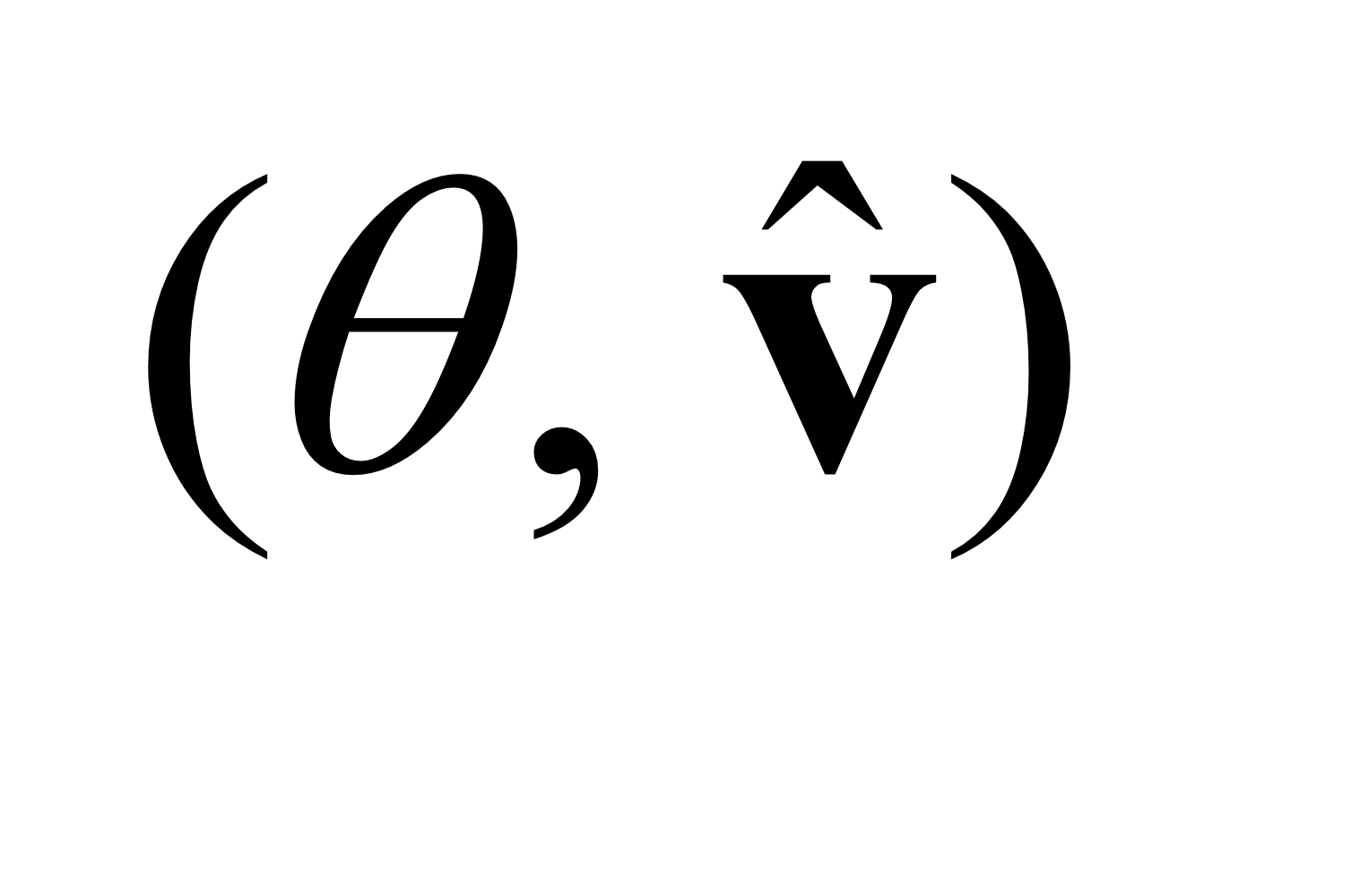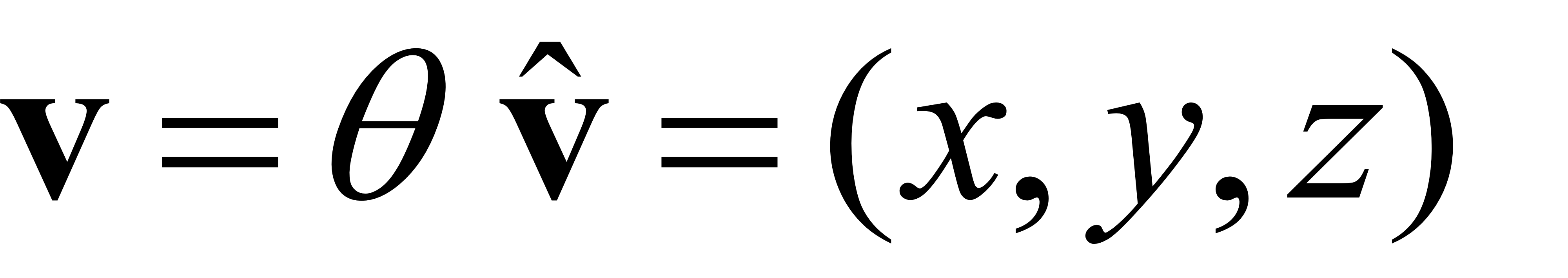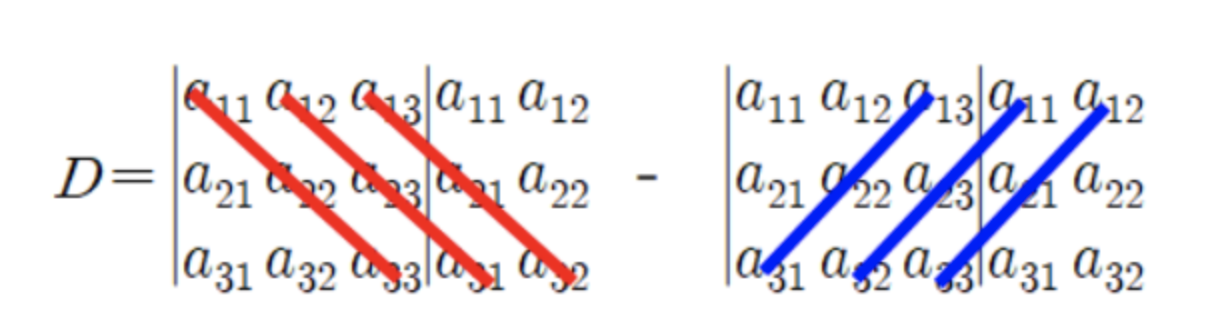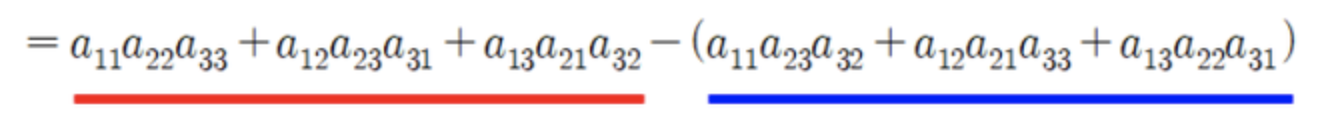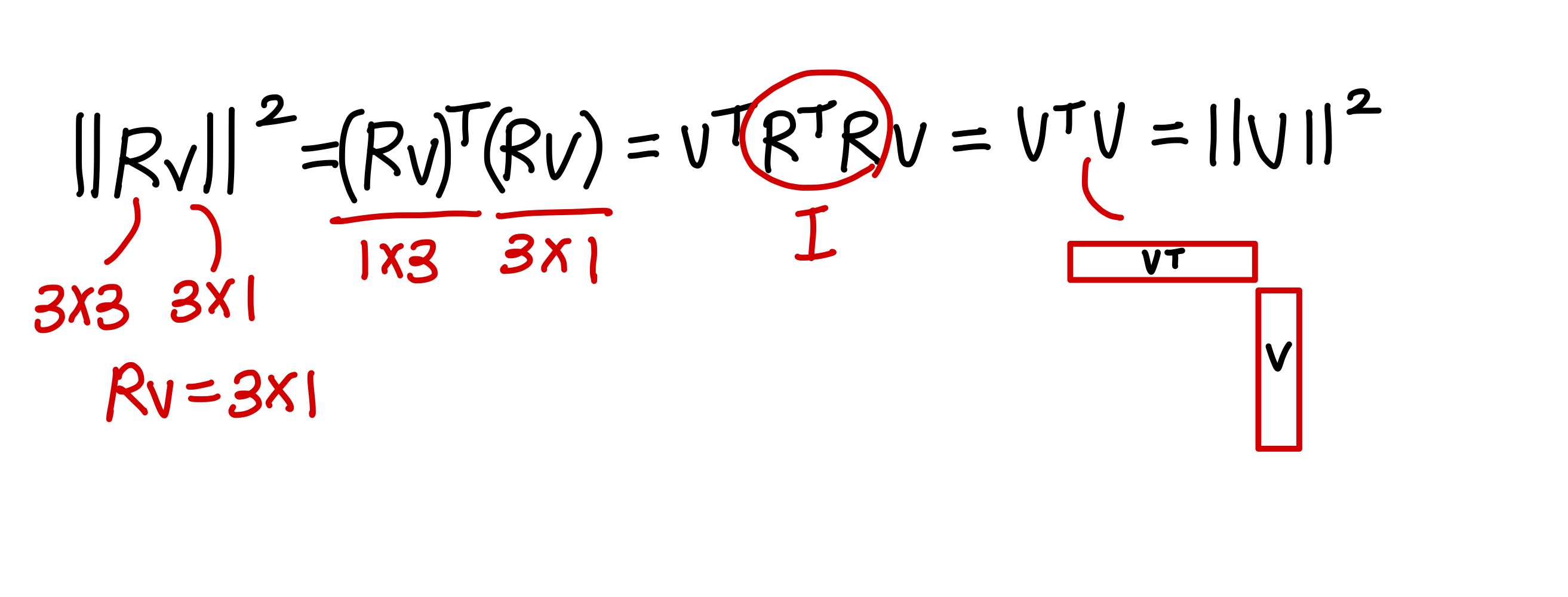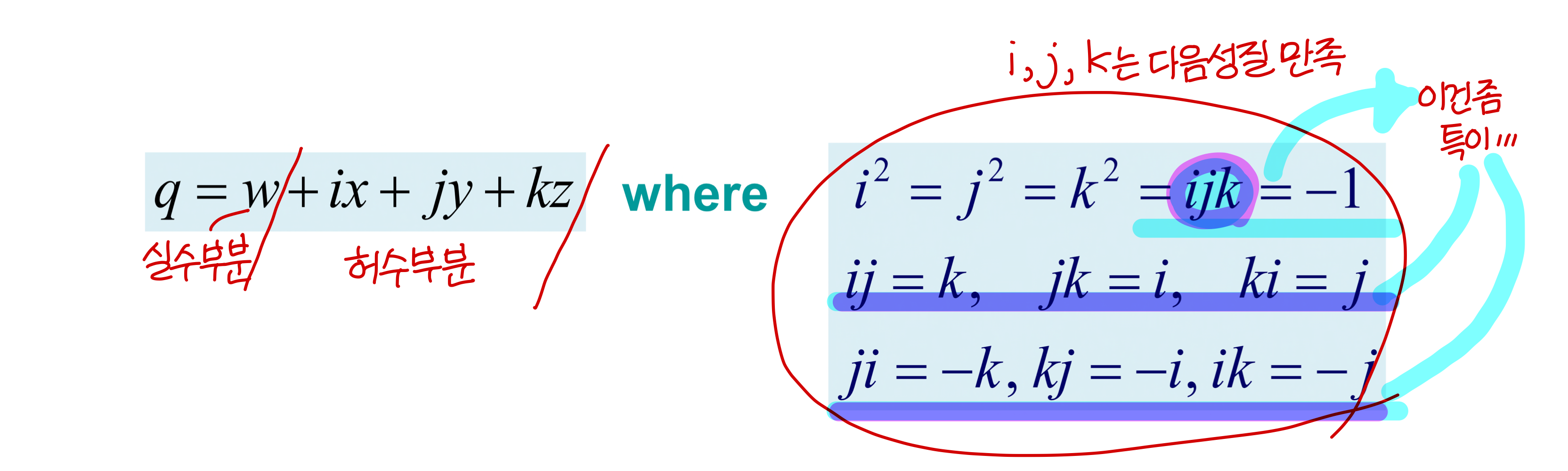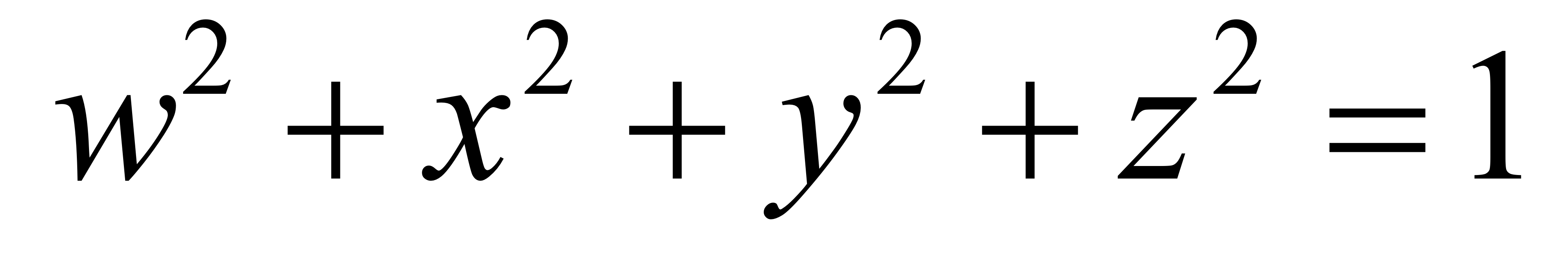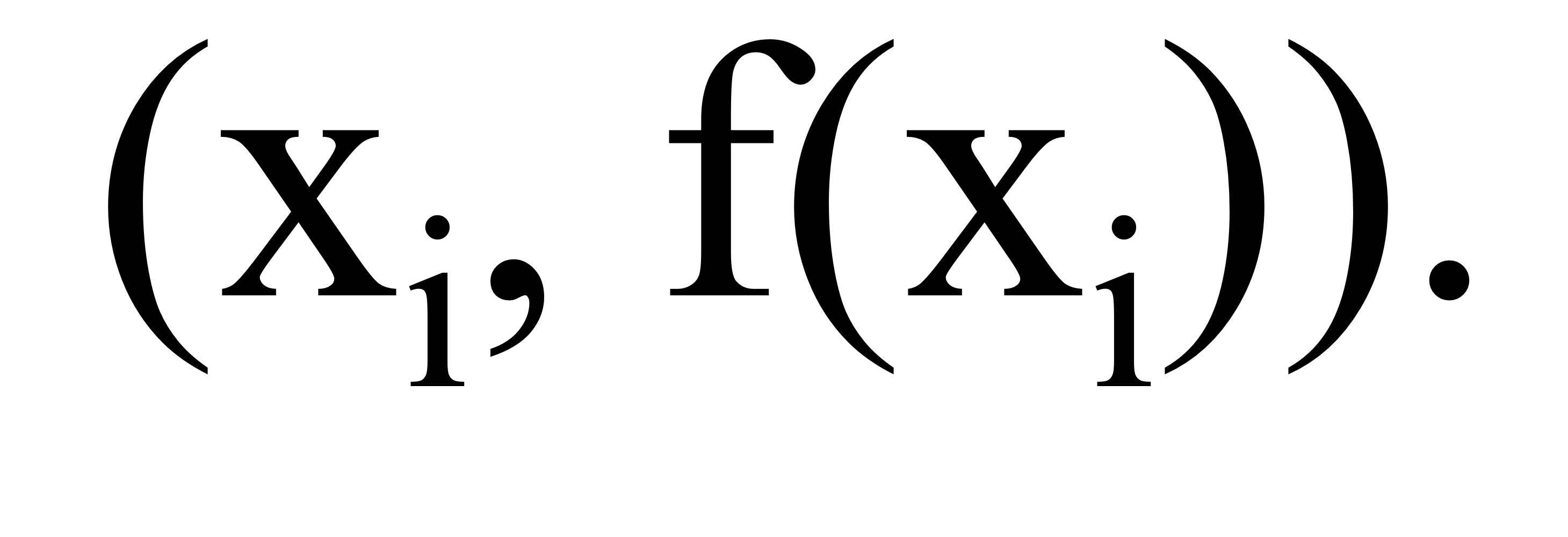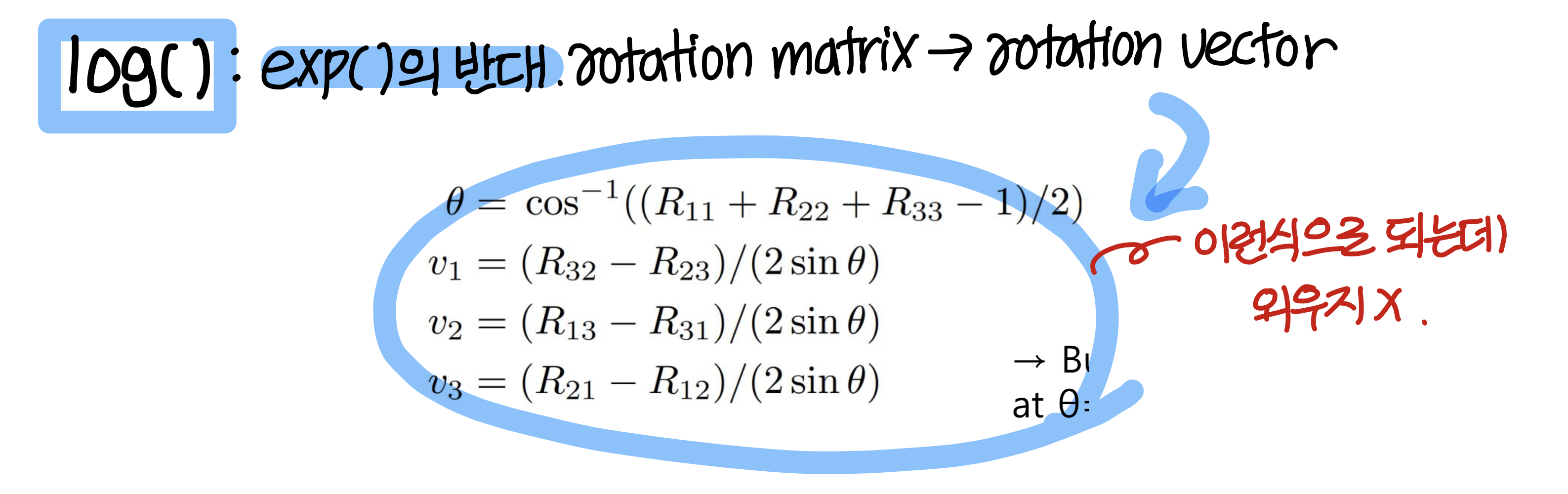Orientation vs Rotation, Degree of Freedom
Orientation vs Rotation
- Rotation : Circular movement(움직임)을 의미
- Orientation: 어디론가 향하고 있는 state(상태)를 의미
Analogy
- (point: vector) 포인터와 벡터 사이의 관계와 (orientation: rotation) orientation과 roation 사이의 관계는 유사하다.
→ point도 state고 vector도 movement니까
- Pointer & vector
(point) + (point) → UNDEFINED
(point) - (point) → (vector)
(vector) +- (vector) → (vector)
(point) +- (vector) → (point)
- Orientation & rotation
(orientation) + (orientation) → UNDEFINED
(orientation) - (orientation) → (rotation)
(rotation) +- (rotation) → (rotation)
(orientation) +- (rotation) → (orientation)
물론 여기서 +, - 기호는 벡터의 +, - 랑은 다르다.
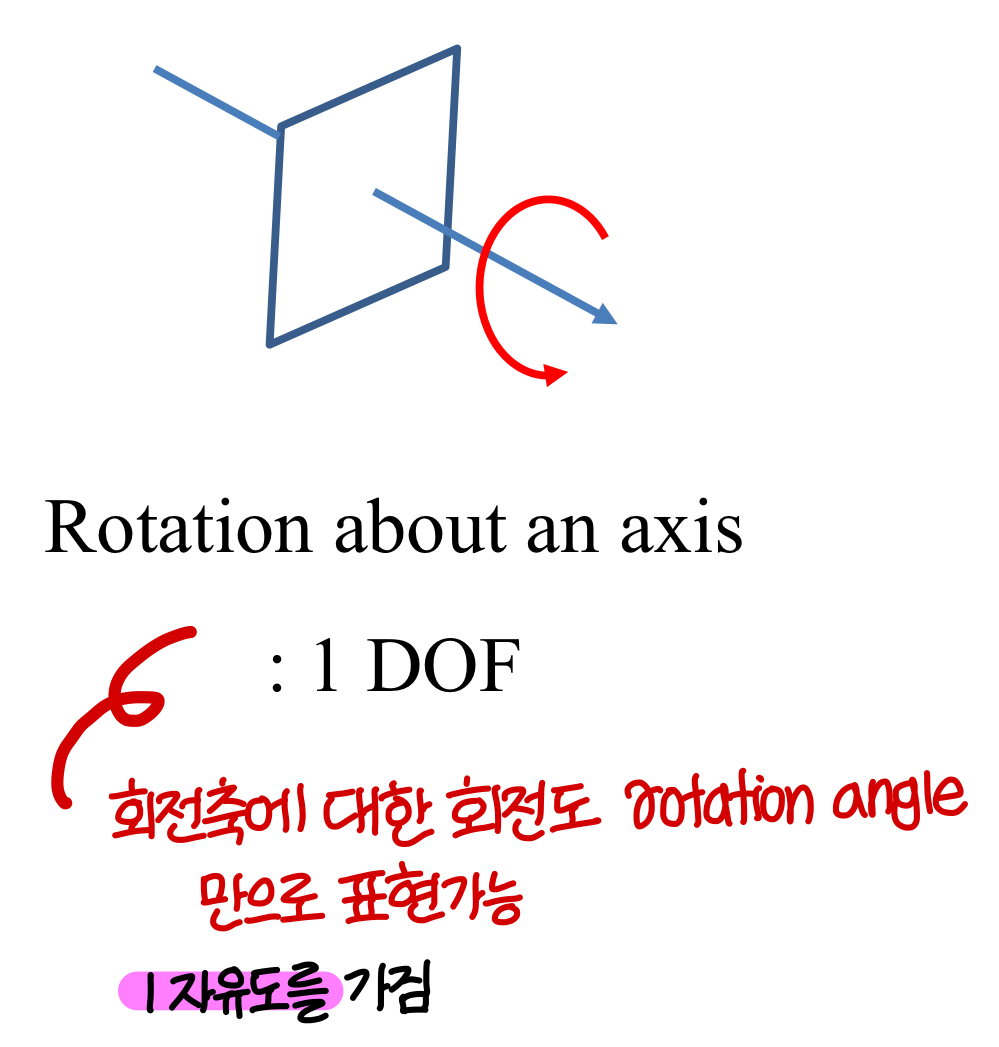
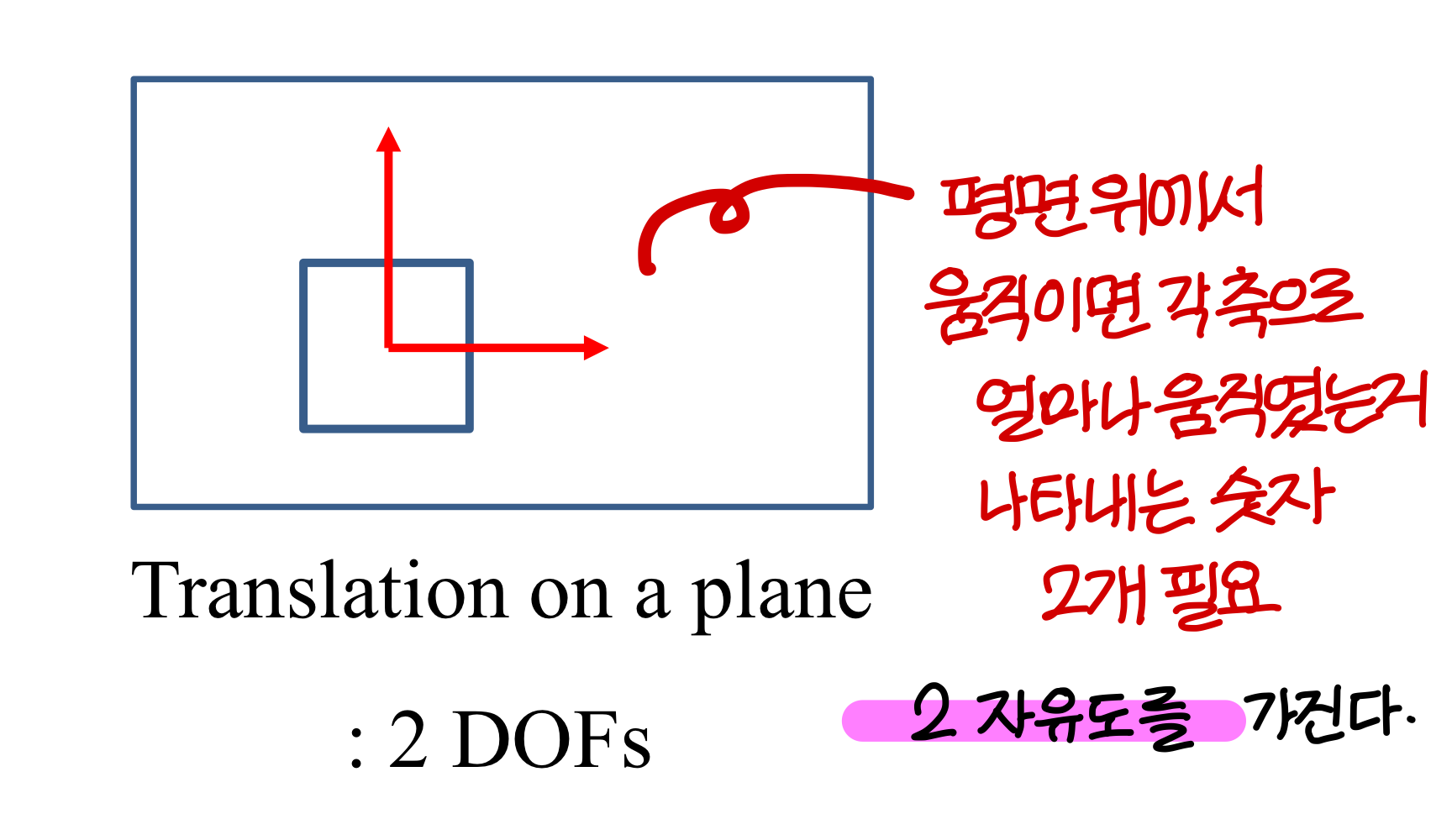
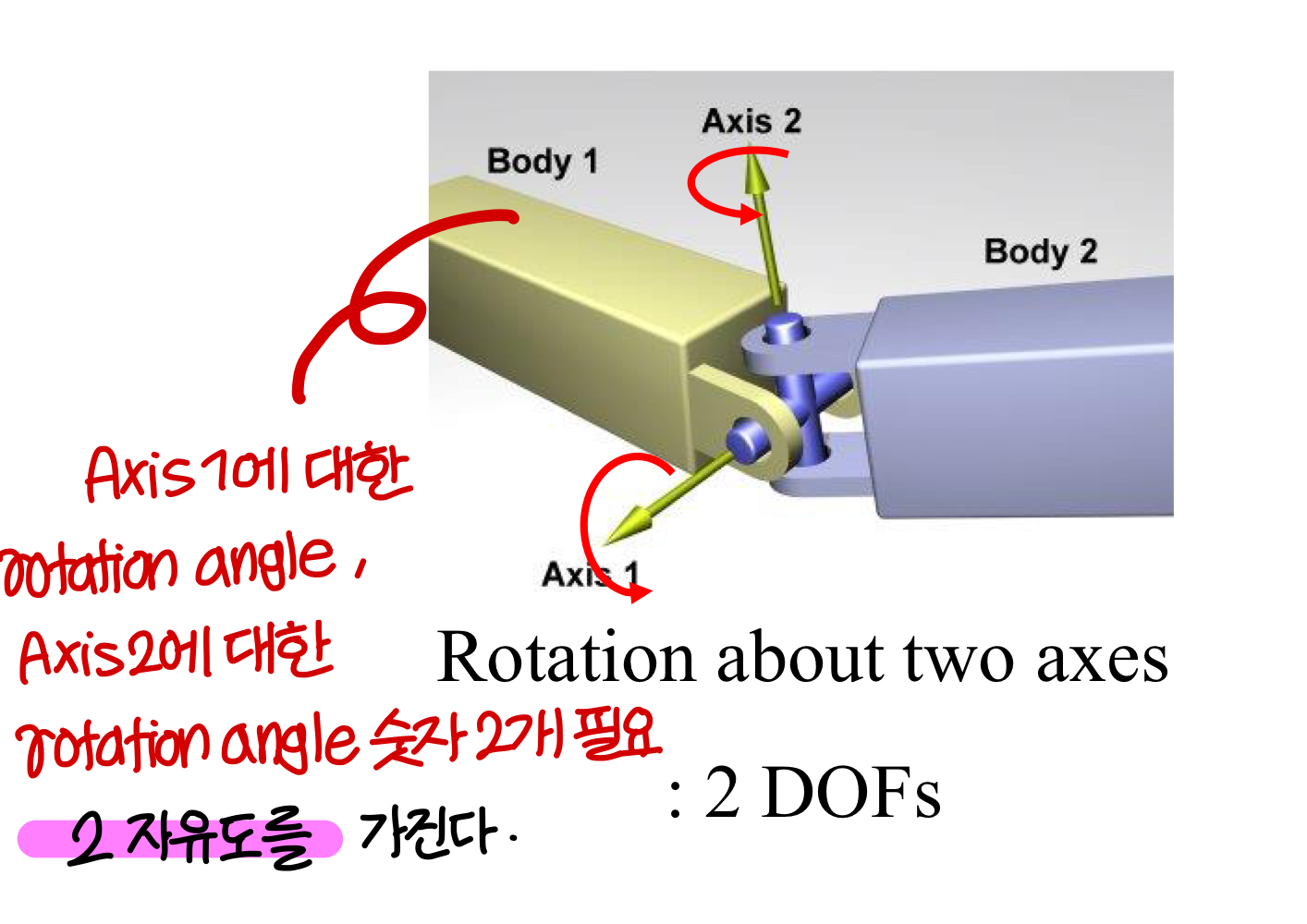
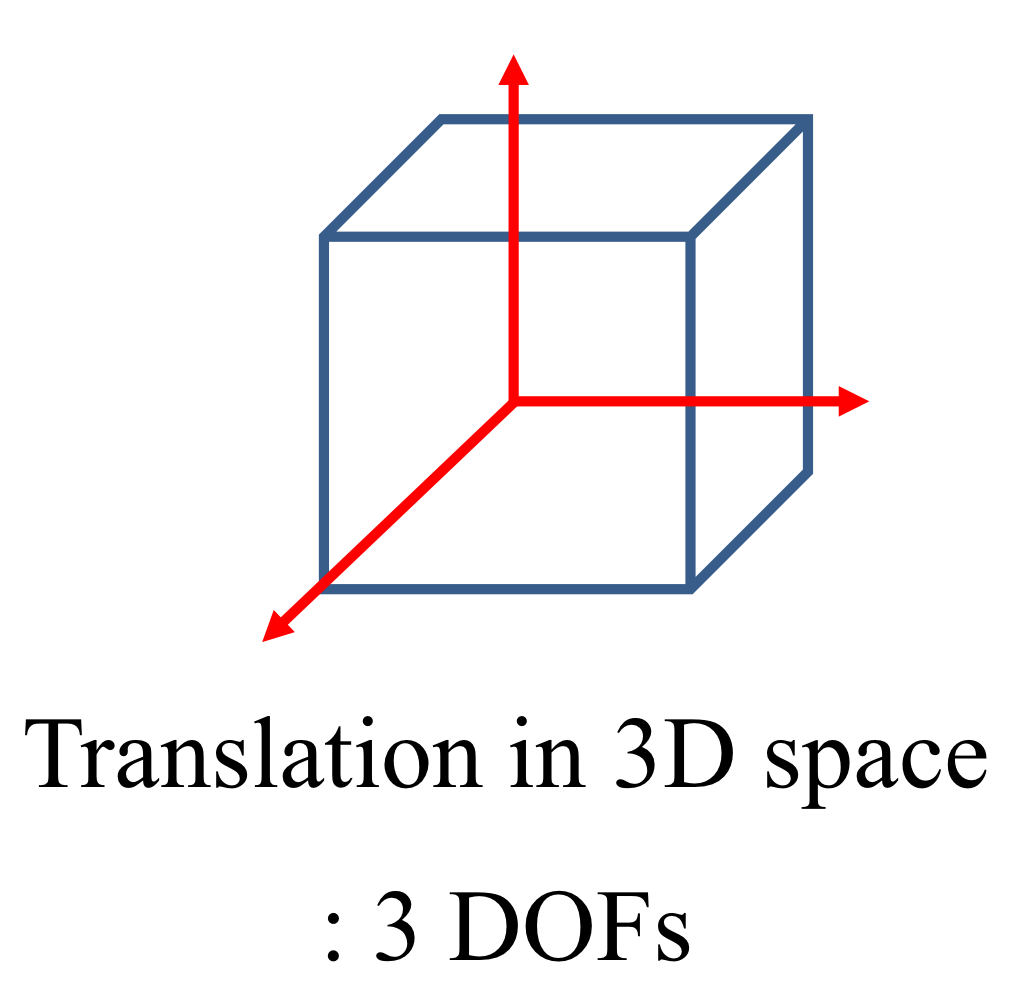
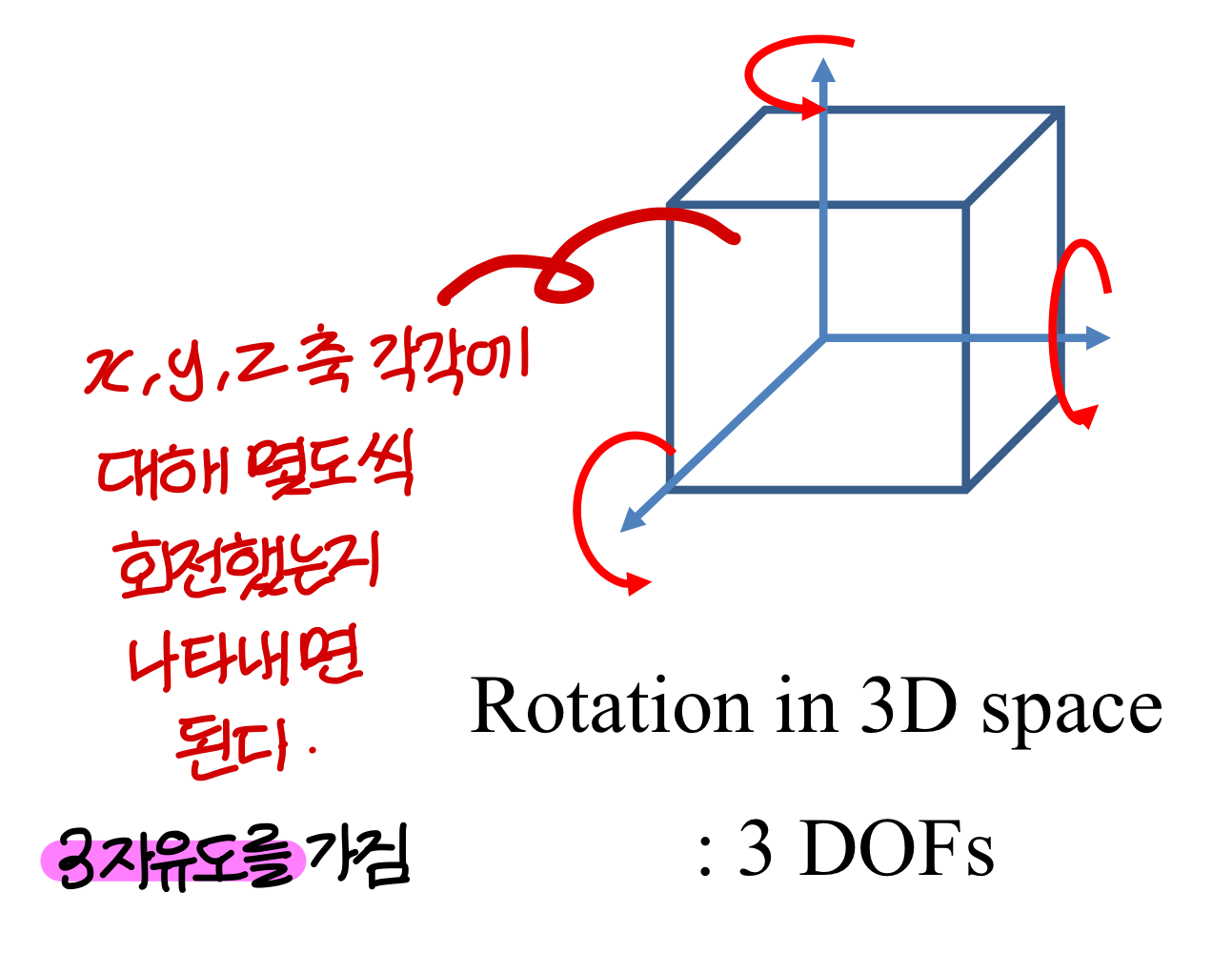
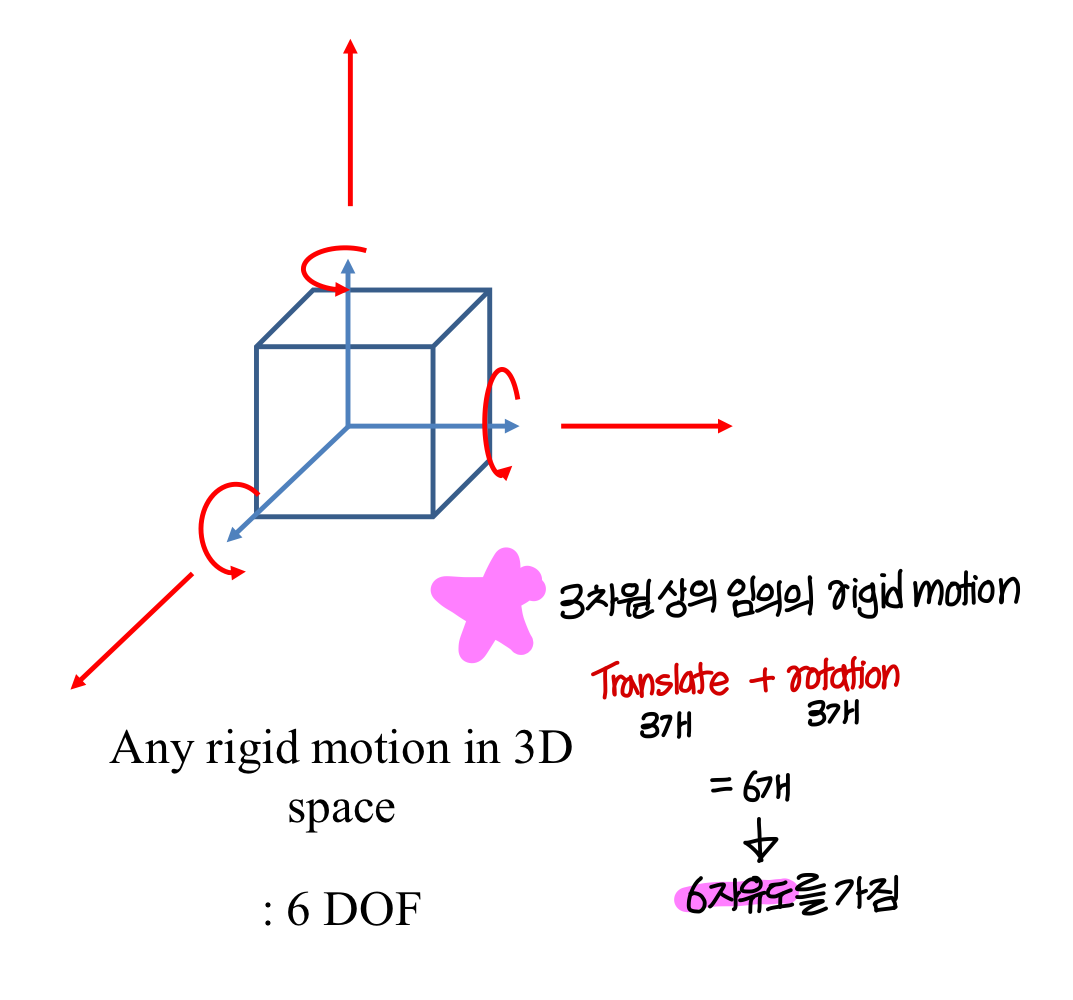
Degrees of Freedom (DOF) → 자유도라고 부름
"상태"를 표현할 수 있는 independent parameters 의 개수
(The number of independent parameters that define a unique configuration)
3D Orientation & Rotation Representation
3D Rotation
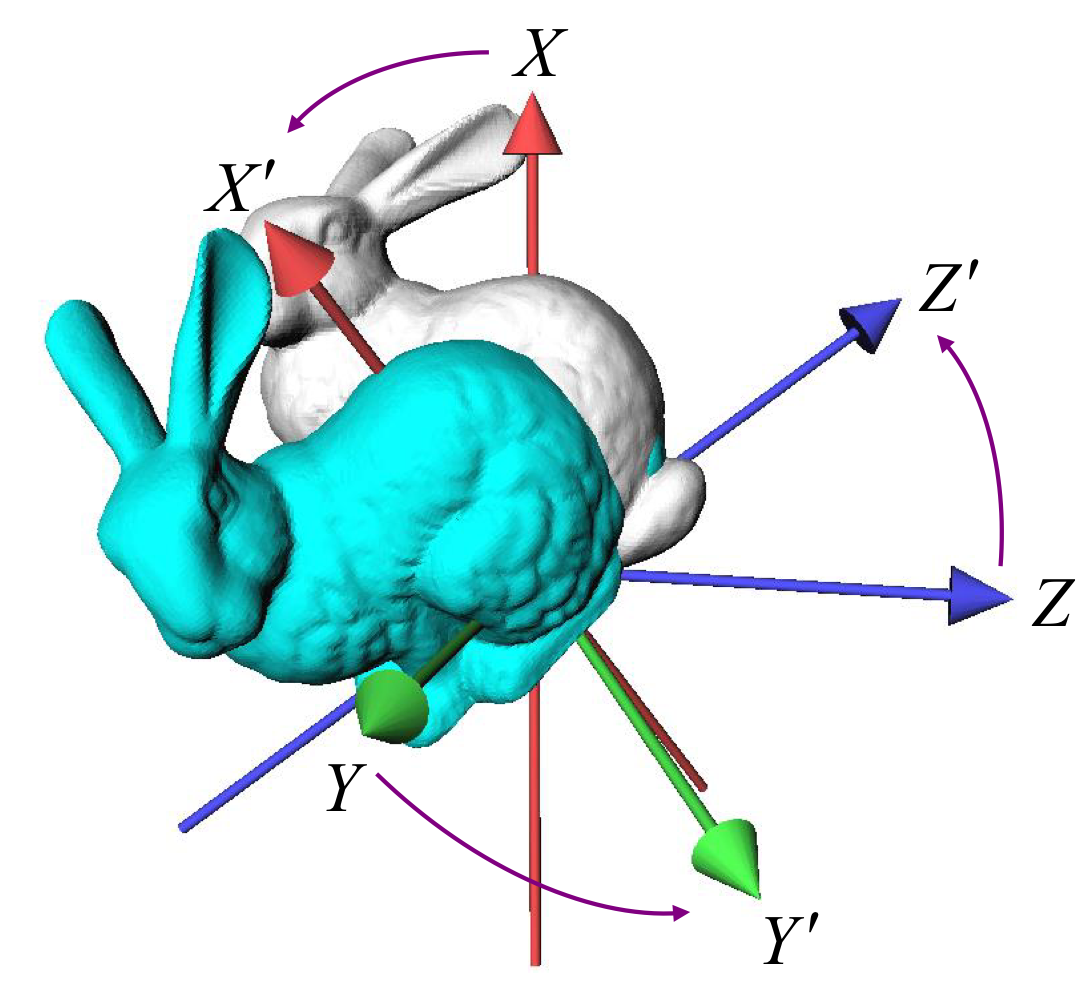
→ 파란색 토끼랑 하얀색 토끼는 서로 다른 orientation을 가지고 있다.
→ 하얀색 토끼가 파란색 토끼가 되도록 하는 rotation을 생각해보자.
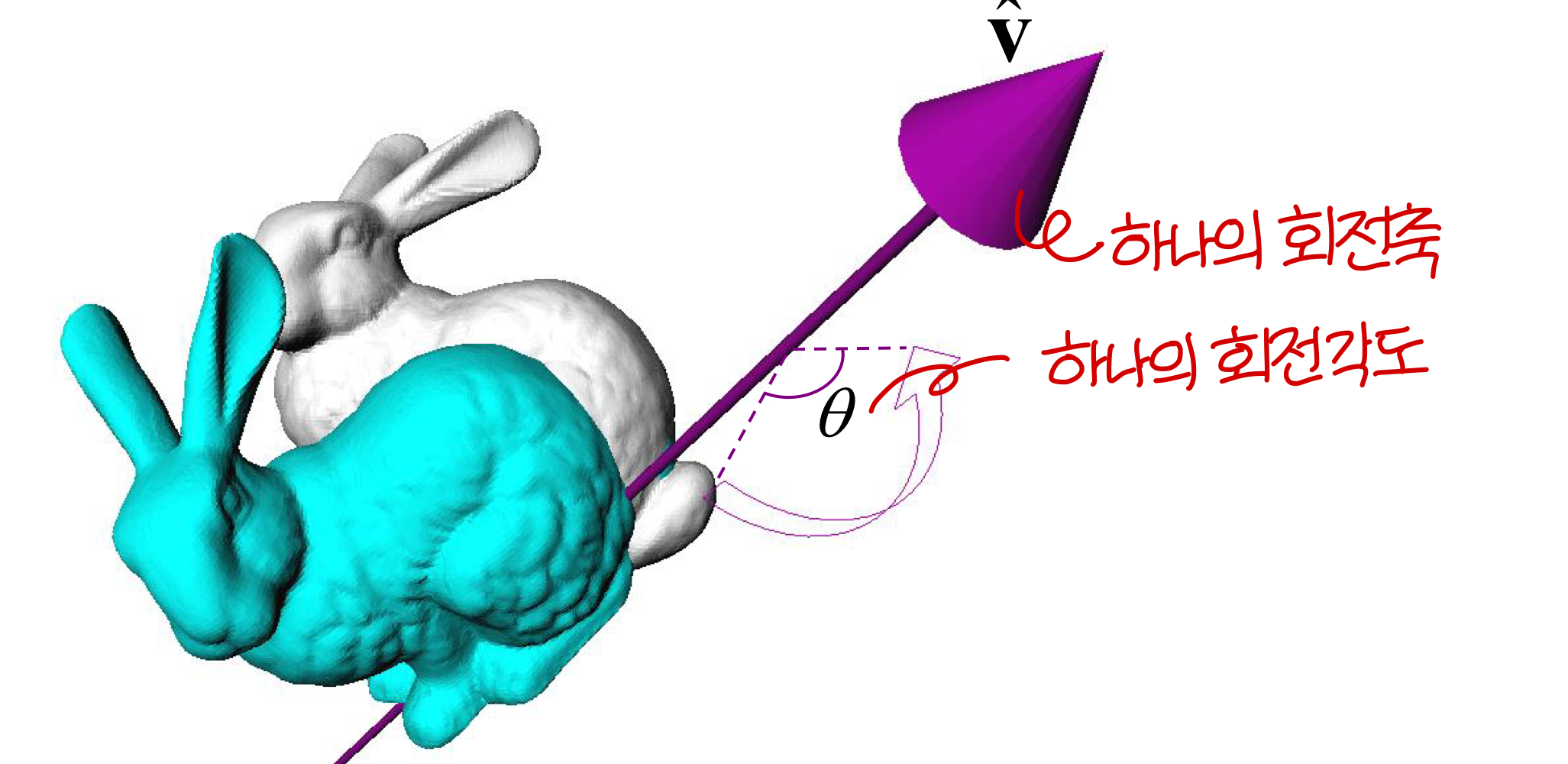
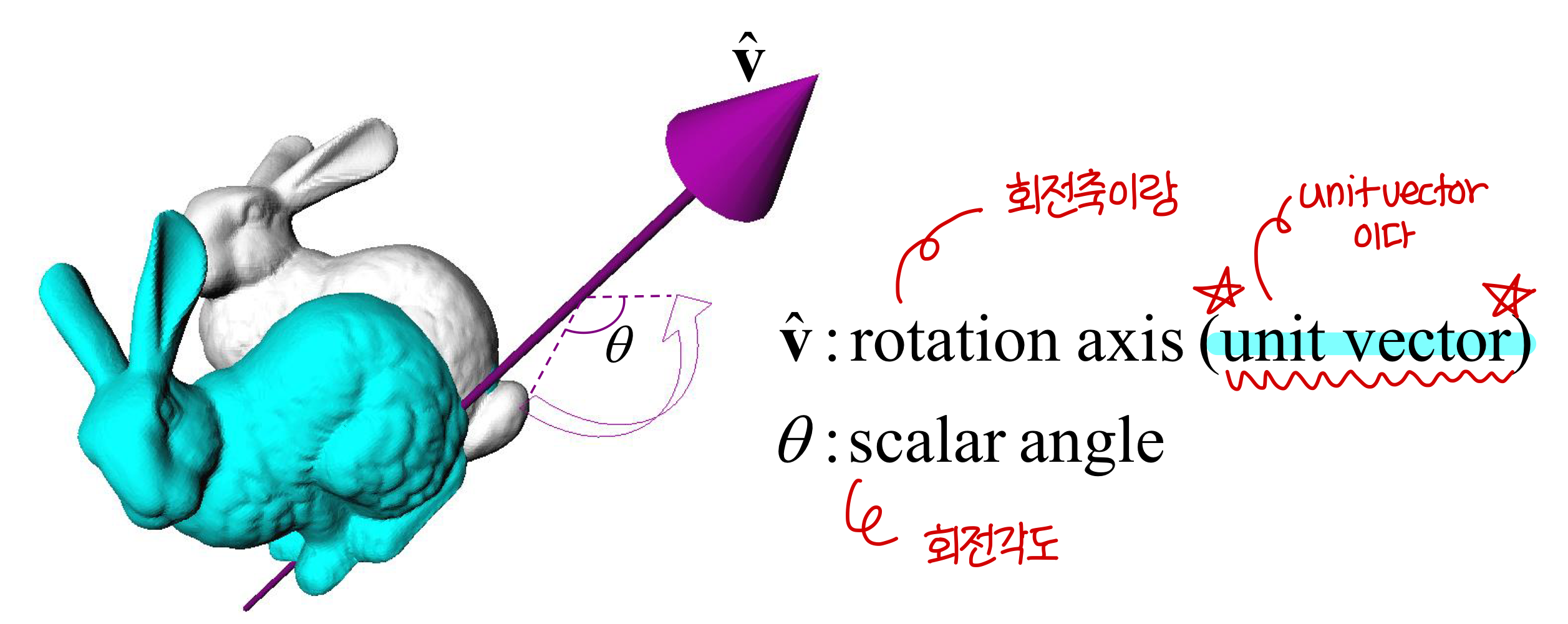
Euler's Rotation Theorem
방금 위에서 말한게 Euler's (오일러의) rotation theorem 이 의미하는 바임.
<Euler's Rotation Theorem>
= 다른 말로 표현하면, 3차원 공간상의 어떠한 회전은 하나의 회전축에 대한 하나의 회전으로 표현할 수 있다.
Describing 3D Rotation & Orientation
2D 에서의 rotation은 기준으로부터의 회전각도로 표현이 가능하다. but 3D는 조금 더 복잡
3D rotation과 orientation을 서술하는 방식에 4가지가 있음
- Euler angles
- Rotation vector(Axis angle)
- Rotation matrices
- Unit quaternions
Euler Angles
- 3D rotation을 3개의 principle axes (이 축은 변할 수 있음) 에 대한 rotation 각도로 표현
Example: ZXZ Euler Angles
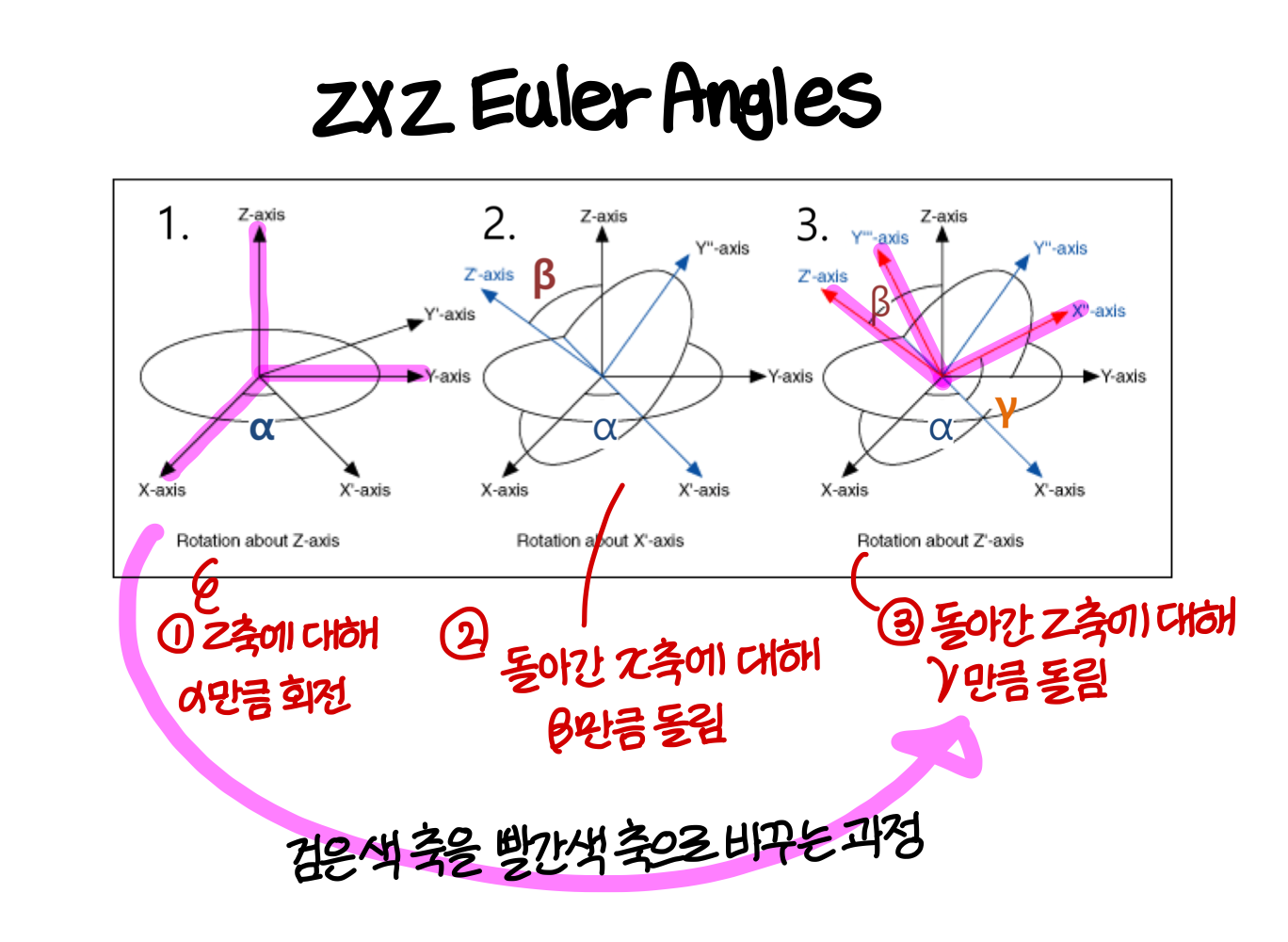
이렇게 회전한 각도 알파, 감마, 베타로 회전을 표현할 수 있다.
위에서 본 걸 rotation matrix로도 표현할 수 있다. 이건 local frame에 대해 적용해나가는거니까

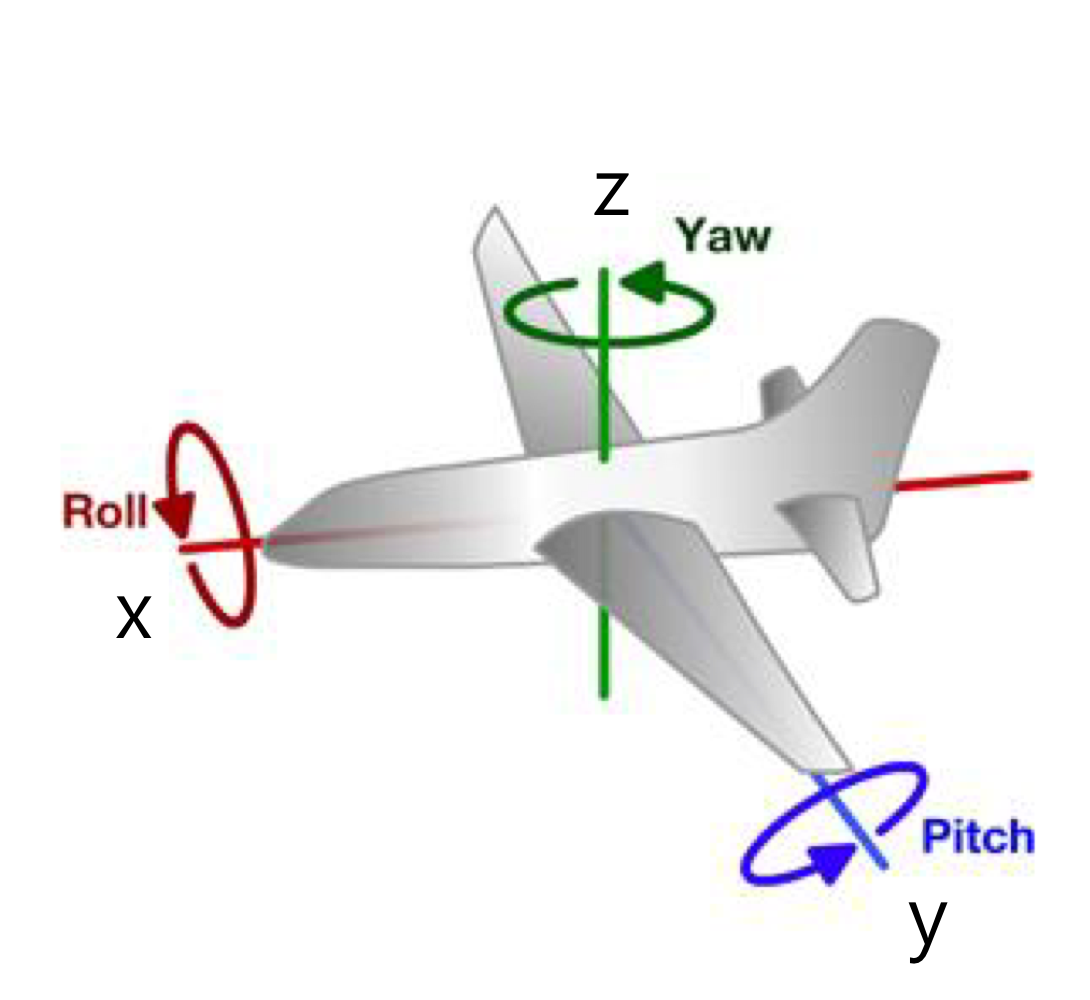
Example: Yaw-Pitch-Roll Convention (ZYX Euler Angles)
- 항공기의 각도를 나타낼때 ZYX Euler Angle를 많이 사용한다.
- Z축에 대해 yaw angle 만큼 Rotate를 한다.
(비행기 방향 정하기)
- Y축에 대해 pitch angle만큼 Rotate를 하기
(Y축은 비행기 날개 두개를 지나는 축)
(고도를 높이면서 갈지, 낮추면서 갈지 결정하는거)
- X축에 대해 roll angle만큼 Rotate를 하기
(비행기 날개를 오른쪽으로 틀면서 갈지, 왼쪽으로 틀면서 갈지)
→ 이 순서대로 기술하는게 상식적으로 타당하다.
→ 그래서 ZYX Euler Angles를 많이 사용하는거
Recall: Rotation Matrix in 3D
Euler Angles
- 12개의 combinations이 가능하다. (3*2*2 = 12)
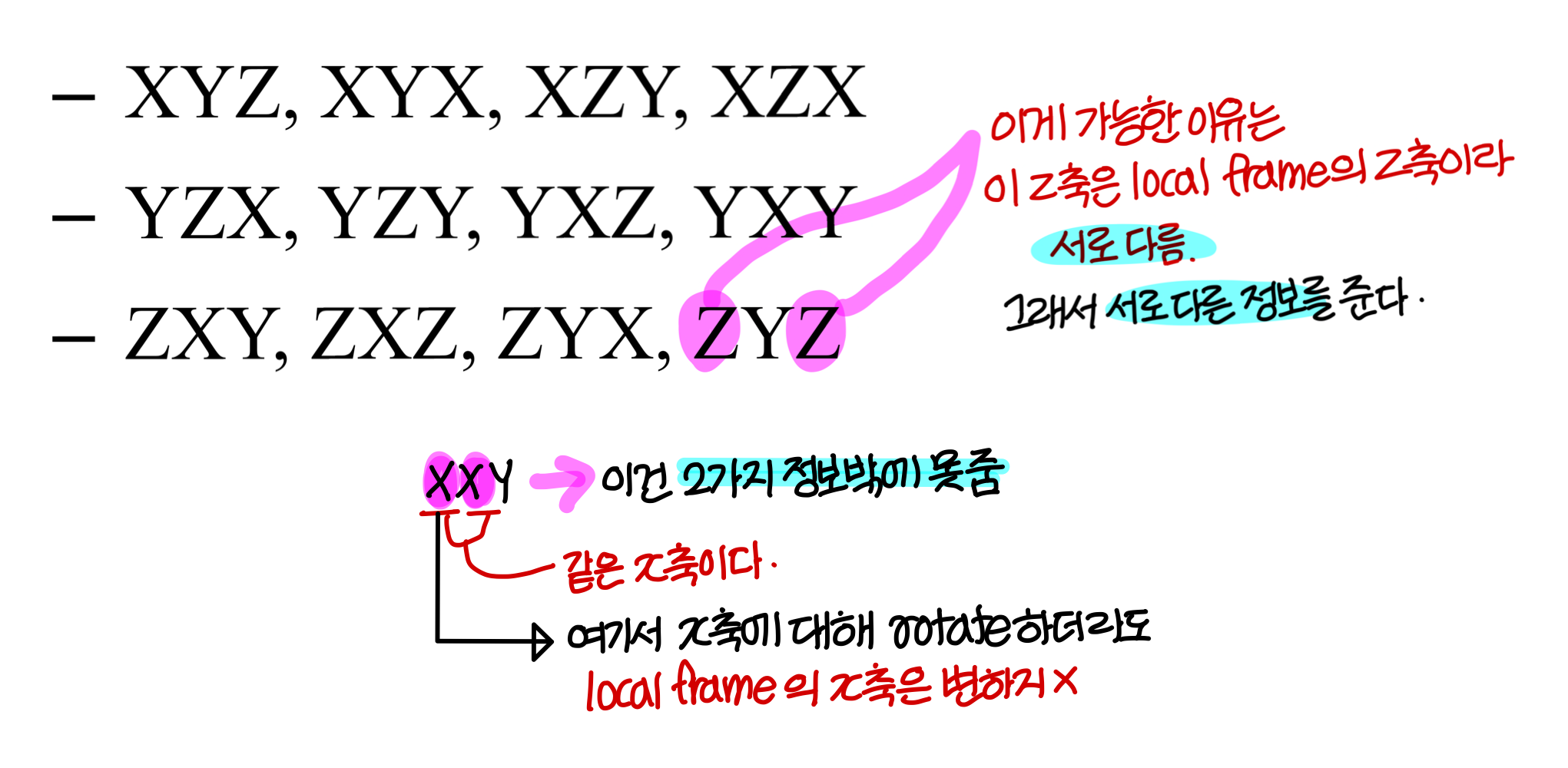
Gimbal Lock
- 그런데 Euler angles는 'gimbal lock'이라는 potential problem을 가지고 있음
- Gimbal Lock: 짐벌 2개가 align 되는 경우 자유도를 하나 잃어버리게 된다. (pitch를 90으로 맞추면 짐벌 2개가 나란해진다.)
→ 이렇게 되면, 비행기, 배의 조종이 정확하지 않게 된다.
[Practice] Euler Angles in OpenGL

Quiz #1

Rotation Vector (Axis Angle)
- Rotation vector랑 Axis angle는 사실상 같은 방법이다.
: 회전축과 회전각도로 Rotation을 표현하는 방법임
Discontinuity (or Many-to-one Correspondences Problem)
- Euler angle이랑 Rotation vector는 3개의 parameters를 사용한다.
→ 그런데, 3D orientation을 3개의 paramenter로 표현하는건 discontinuity 문제가 있다.
<정리하면>
- Euler angles : Discontinuity(or many-to-one correspondences) 이랑 Gimbal lock 문제를 가짐
- Rotation Vector (Axis Angle): Discontinuity(or many-to-one-correspondences) 문제를 가짐
Problem or Representing 2D Orientation by Angle : Discontinuity
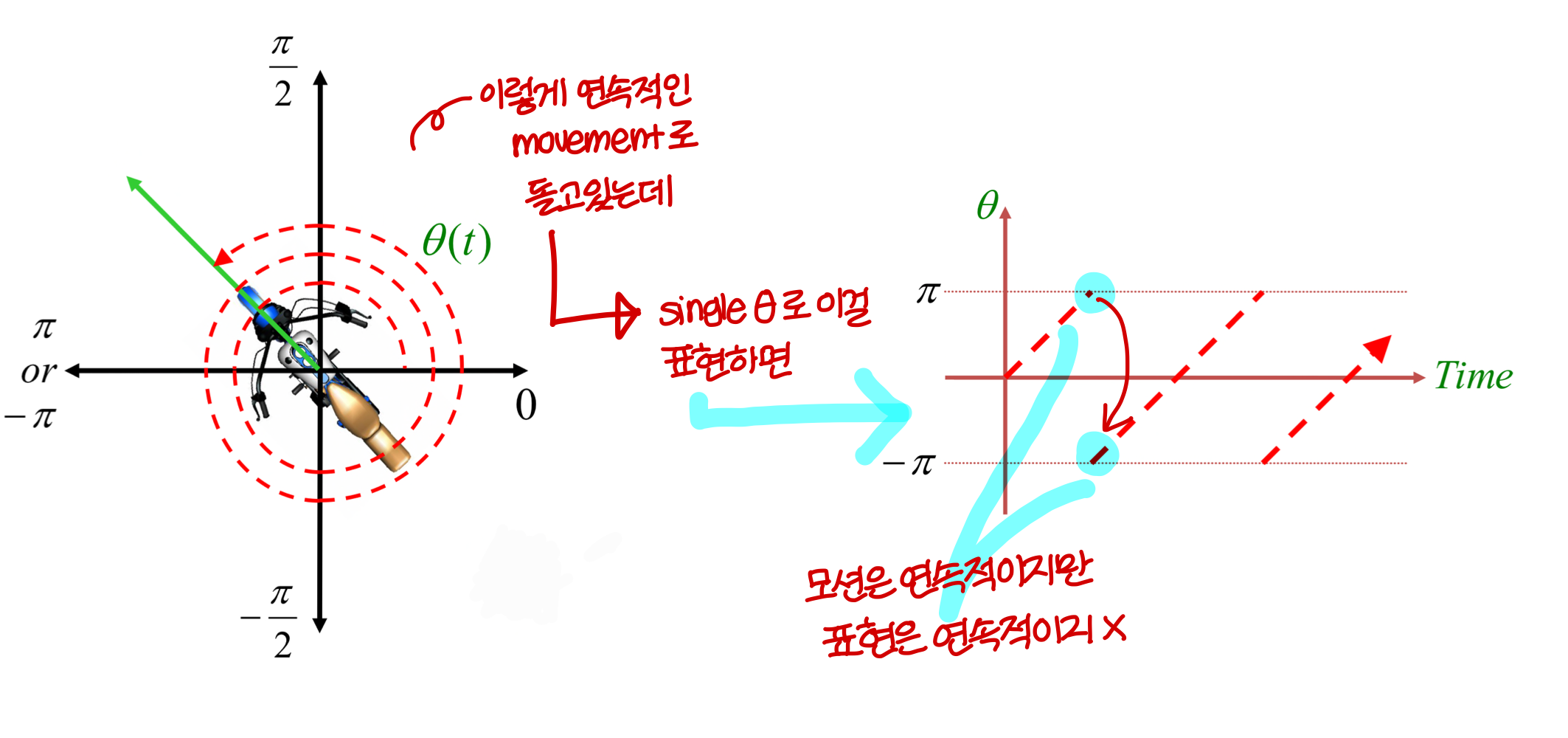

- 이 문제들을 해결하기 위해선, DOFs 보다 더 많은 parameters가 필요하다.
→ 이렇게 해서 나온게
Rotation matrices와 Unit quaternions
- 하지만 Euler angles 는 여전히 meaningful하다.
→ Euler angles가 직관적이기도 하고, Euler angles 방법을 사용하는게 가장 편한 경우가 있음.
3자유도 회전 관절을 표현할 때는 Euler angles 방법을 사용하는게 가장 편하다.
Rotation Matrices
- 3D 상에서의 회전은 3X3 matrix로 표현된다.
ex)
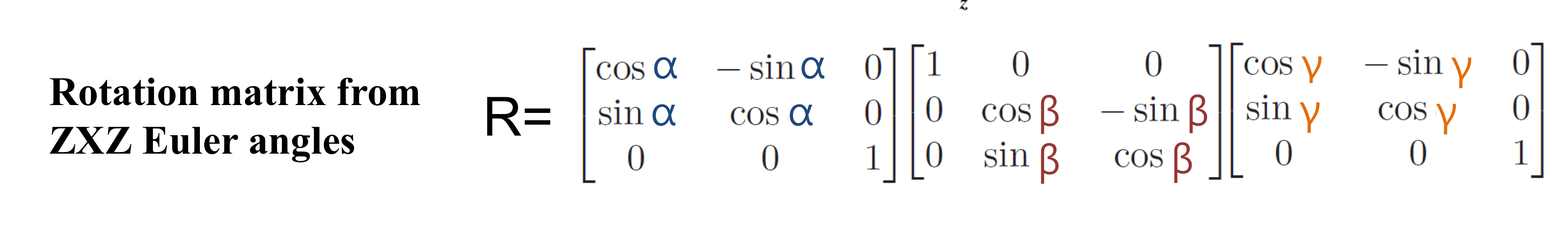
Meaning of Rotation Matrix
- 1) new rotated frame의 orientation
(rotation matrix는 orientation을 직접 지정하기도 한다.)
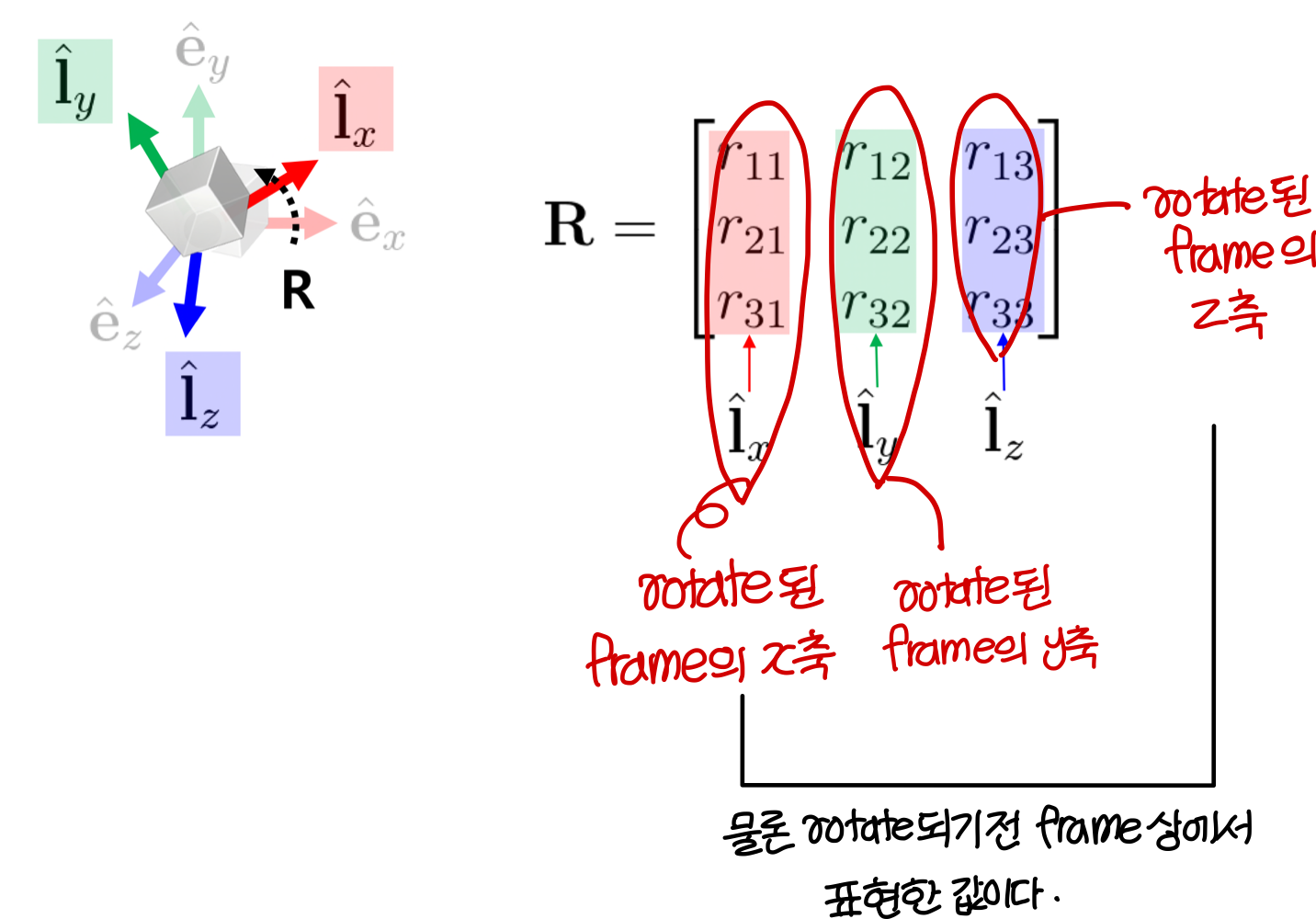
- 2) global frame으로부터 rotated frame으로의 rotation
(시작이 global frame이 아닐수도 있지 않나? 근데 이렇게 표현했네..)
Mathematical Properties of Rotation Matrix
다음 2가지 성질을 만족할 때 rotation matrix라고 부른다.
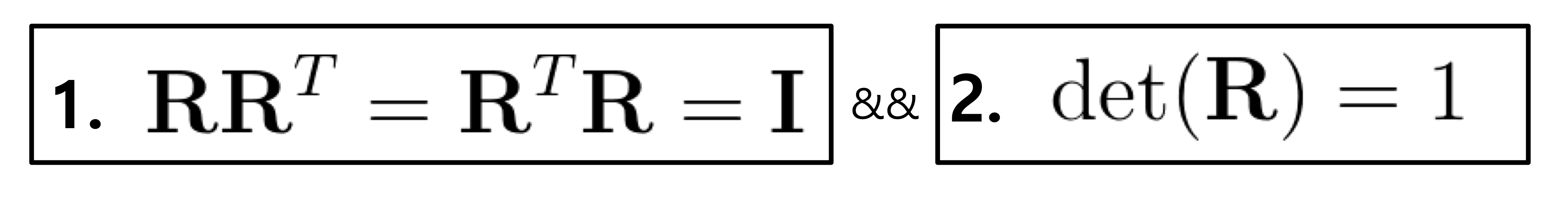
→ 1번째 성질은 orthogonal matrix라는 의미임
orthogonal matrix는 row와 column vector들이 서로 직교하고 다 단위벡터인 matrix를 말한다.
→ determinant 구하는 방법
- 즉, rotation matrix는 determinant가 1인 orthogonal matrix이다.
→ rotation matrix를 special orthogonal matrix라고 부르기도 한다.
→ sizers 3인 rotation matrix의 set을 special orthogonal group, SO(3)이라고 부른다. (3차원 상의 rotation matrix의 집합)
Geometric Properties of Rotation Matrix
- 와 같이 rotation matrix 여러개를 곱한 것도 Rotation matrix이다. (composite rotation)
는 만큼 회전하고, 회전된 프레임을 기준으로 만큼 회전시키는 rotation matrix
<성질 1, 2 만족하는지 확인해보기>
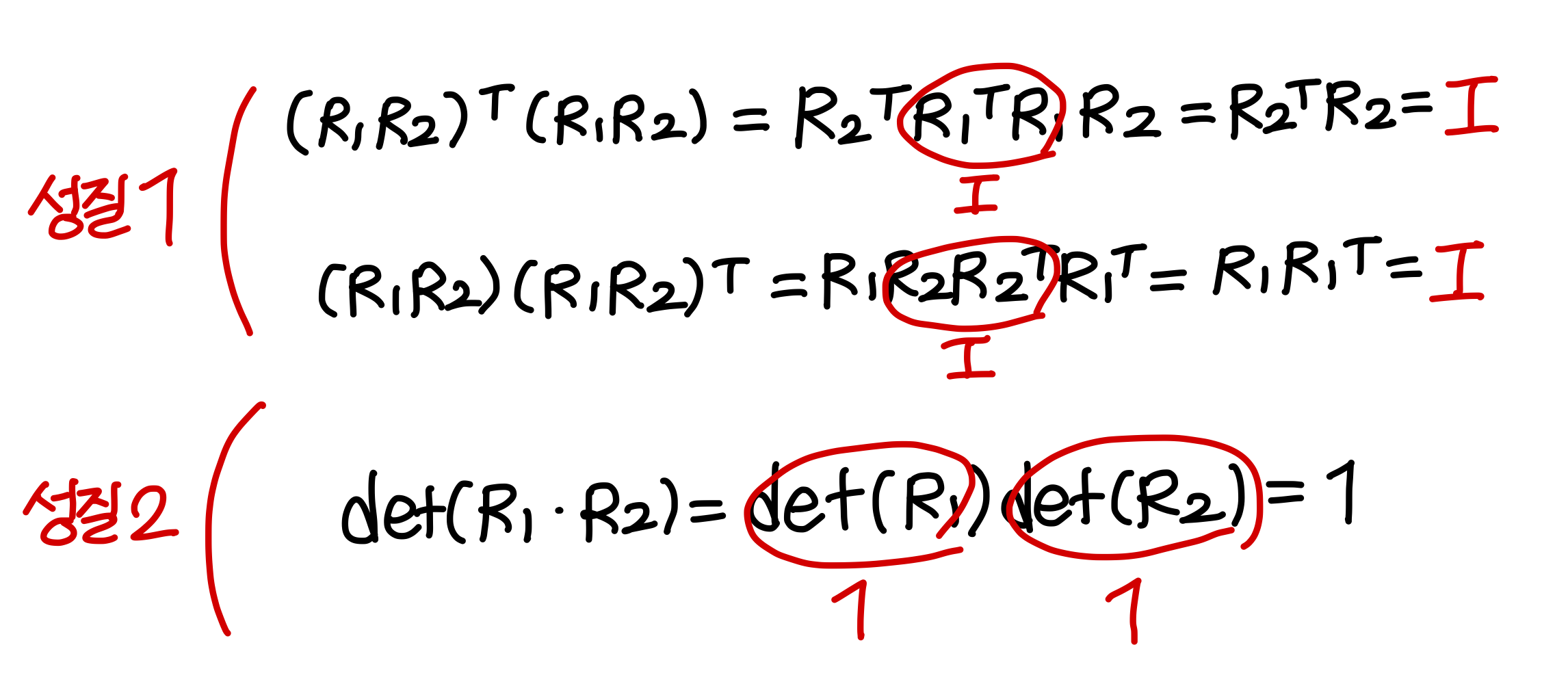
[Practice] Properties of Rotation Matrix
우리 앞에서 Rotation Matrix까지 다 살펴보긴 했다. 몇가지만 추가적으로 확인해보자!
Rotation Matrix for Rotation about an Arbitrary Axis
- Euler's Rotation Theorem이 우리에게 말해준거: arbitrary 3D rotation은 특정축에 대한 하나의 rotation으로 표현할 수 있다!
- 그렇다면 rotation matrix로 특정축에 대한 회전을 어떻게 표현할까? 이렇게 축과 각도가 주어졌을때!
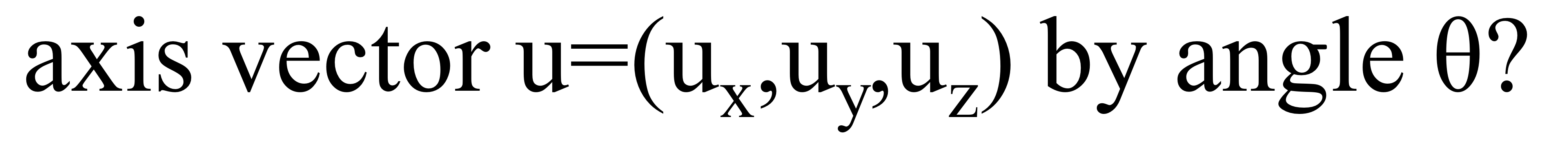
→ 매우 naive하고 비효율적인 방법으로 표현할 수 있음
Step1. u를 z축에 나란하게 회전시키고
Step2. z축에 대해 theta만큼 회전시키고
Step3. 다시 Z축을 original axis(u)로 회전시킨다.
이렇게 Step1에서 나오는 matrix, Step2에서 나오는 matrix, Step3에서 나오는 matrix
3개를 곱하면 u축에 대해 theta만큼 회전시키는 matrix가 나온다.
- 더 효과적인 방법은 Rodrigues' rotation formula (그냥 밑에처럼 공식화 되었다는거...방법은 위에서 말한거랑 같음)
→ u가 normalized axis vector(unit vector)일때 theta만큼 돌리는 Rotation matrix는 다음과 같다.
(외우는거 아님!!!!)
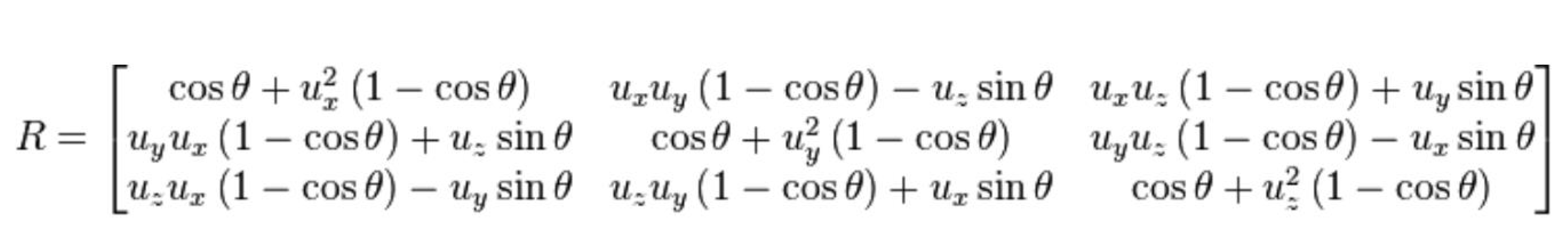
Quiz #2

Quaternions (간단히만 볼꺼임)
Which Representation to Use
- 3D orientation & rotation representation 하는 방법 4가지를 살펴봤음
1) Euler angles
2) Rotation Vector(Axis-Angle)
3) Rotation matrices
4) Unit quaternions
→ 이 4가지 방법을 배웠는데 이 중 뭘 써야할까?
- General recommendation: rotation matrices와 unit quaternions를 일반적으로 사용한다.
→ 이유) Euler angles와 Rotation vector는 gimbal lock 또는 discontinuity(many-to-one correspondence) 문제를 가지고 있기 때문
Rotation matrices와 unit quaternions는 위의 문제를 가지고 있지 않다. 왜냐하면 DOFs보다 많은 숫자를 사용해서 3D orientation/rotation을
표현하기 때문
(rotation matrix: 9, unit quaternion: 4)
Rotation Matrix vs Unit Quaternion
- 둘의 표현 범위는 동일하다. converted from & to axis-angle representation이 가능하다.
그럼 둘 중 뭐쓰지???
<quaternions가 좋은 점>
- 파라미터 수가 더 작음 (Rotation matrices는 9개고 unit quaternions는 4개니까)
- 계산이 더 간단하다. (Simpler algebra)
- 길이가 1에서 점점 벗어나게 될텐데 이를 보정해주기위한 normalize 작업이 간단하다. (Easy to fix numerical error)
<rotation matrices가 좋은 점>
- One-to-one correspondence
quaternions는 2:1대응임. 하나의 orientation을 의미하는 quaternions가 2개임. q= -q이기 때문에
quaternions는 이런 성질 때문에 생각하지도 못한 문제들이 발생하기도 한다.
- rotation과 translation을 동일한 방법으로 처리할 수 있다. (4X4 homogeneous matrices를 사용해서!)
Conversion Between Representations

→ 결국, 3차원 회전, orientation을 의미하는 4가지 방법끼리 서로 converting 가능
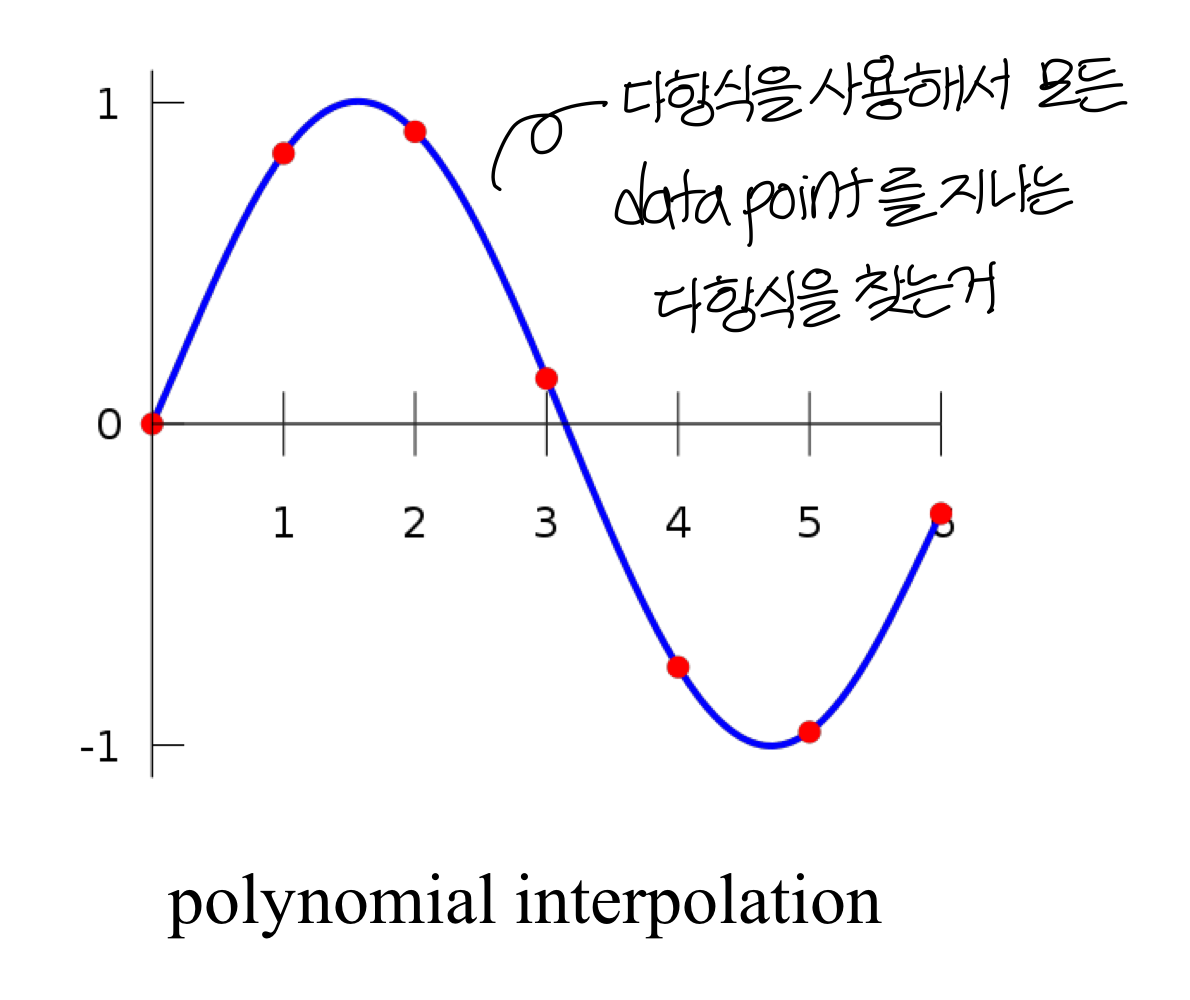
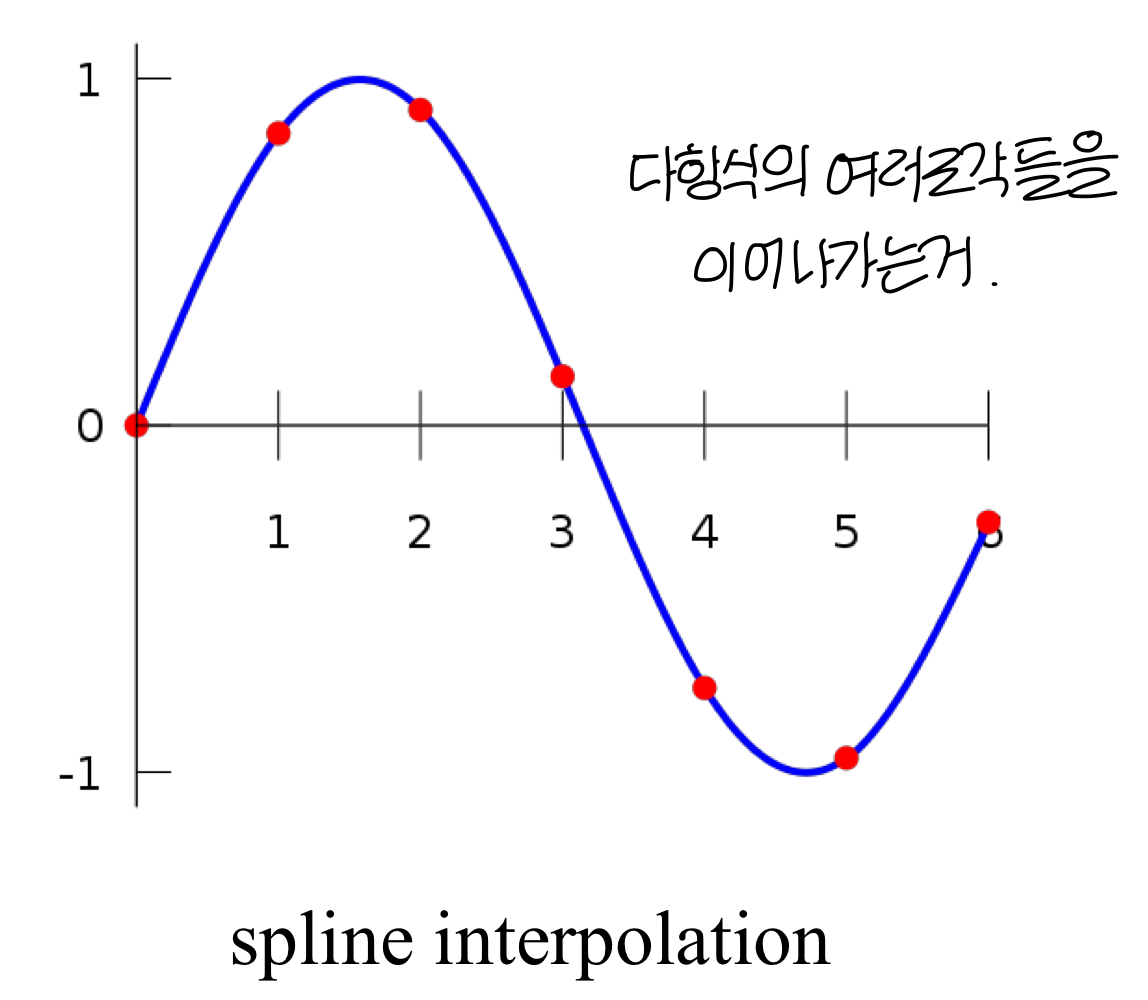
3D Orientation Interpolation
Interpolation
- Interpolation은? 몇개의 알려진 data point가 있으면 이걸 이용해서 새로운 data point를 구상하는 과정
→ 다른 말로,
- interpolation의 방법 4가지
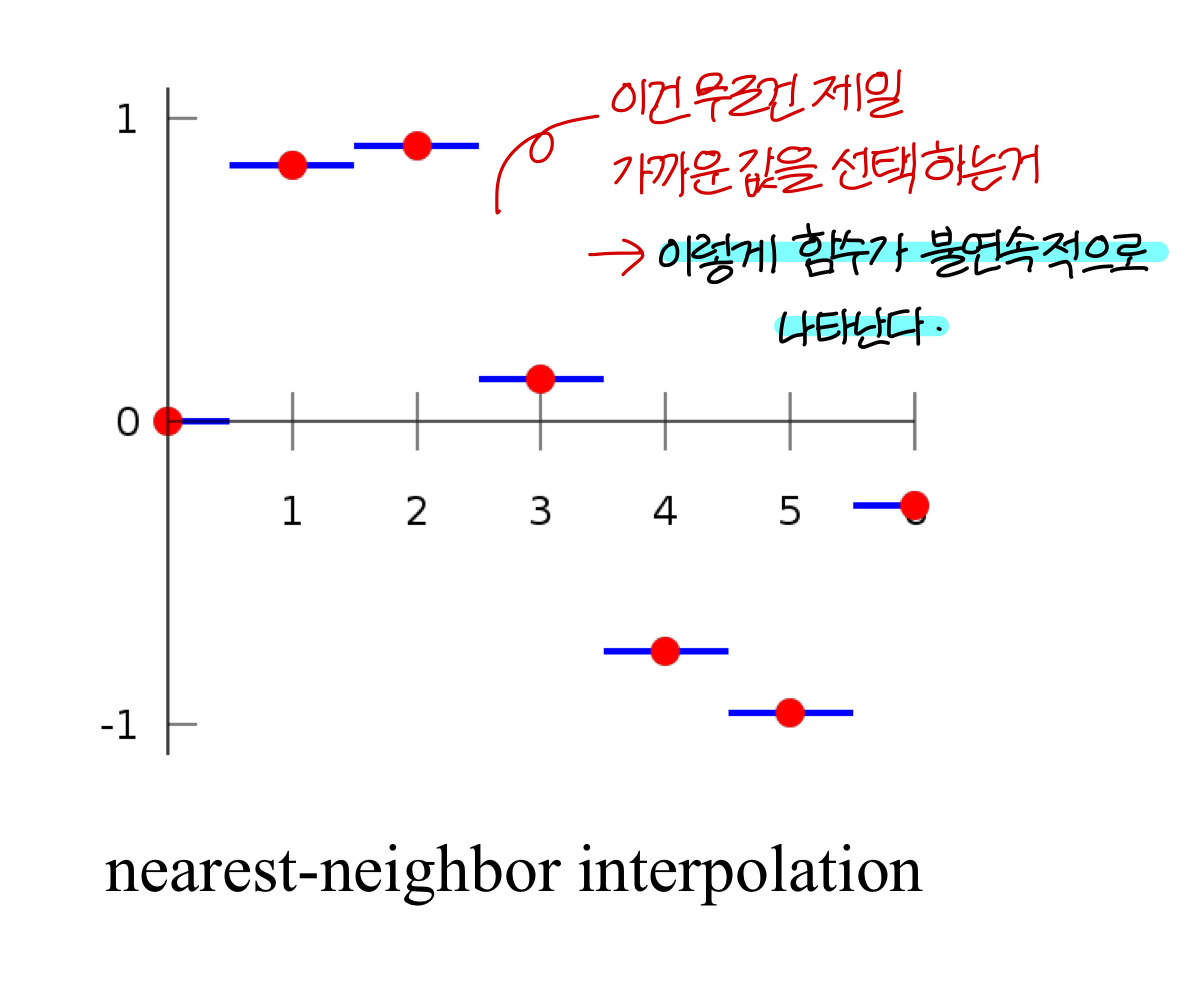
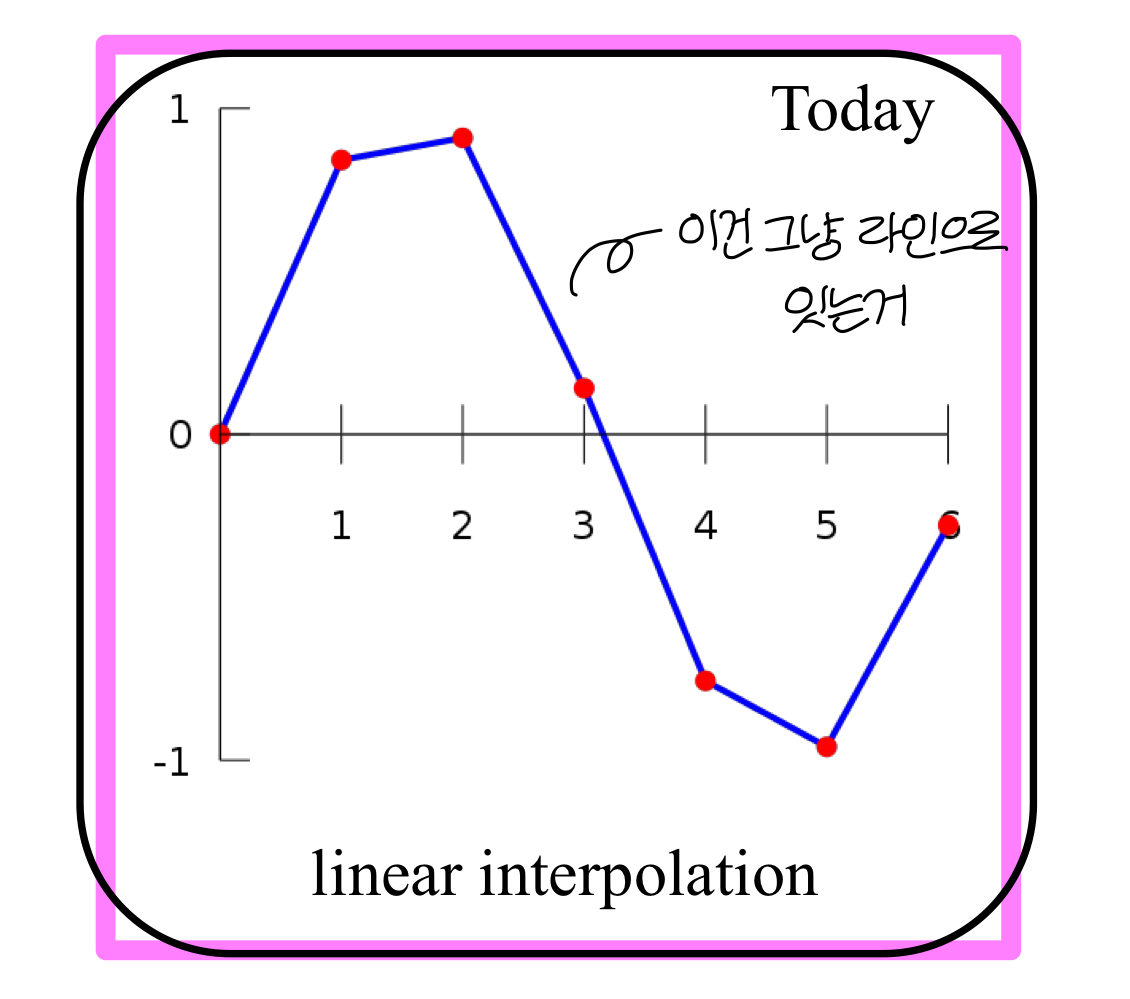
Linear Interpolation
t = 0에서 t = 1로 이동하는 동안 point a 쪽에서 point b 쪽으로 움직임
→ a라는 translation과 b라는 translation이 있을 때 이거 2개를 이을려고 하면 오른쪽의 코드처럼 하면 된다.
Linear Interpolation for 3D Orientation
translation은 위에처럼 간단하게 하면 된다.
그런데 orientation에 대해선 조금 더 생각해봐야한다!!!
→ orientation은 표현 방식이 여러개인데 모든 방법에 대해서 아까 코드와 같은 방법 적용해도 될까? No!
Interpolationg Each Element of Rotation Matrix
- 그냥 생각해도 rotation에 대해 linear interpolation 할 때처럼 하면 안될것 같지만 구체적으로 예를 살펴보자.

→ unit quaternions의 (w, x, y, z)의 각 숫자를 interpolating 해도 roation matrix의 경우처럼 말이 안된다.
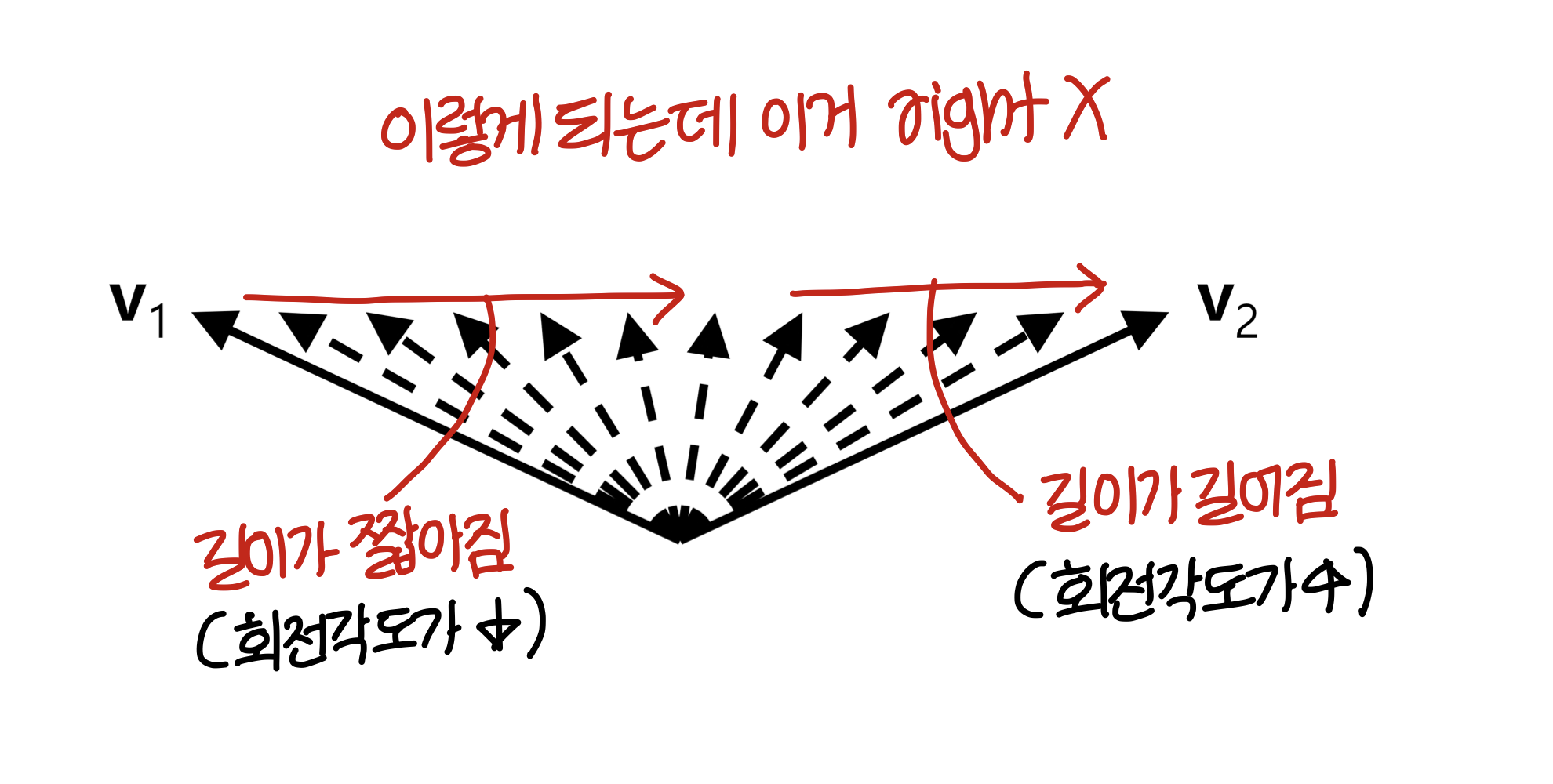
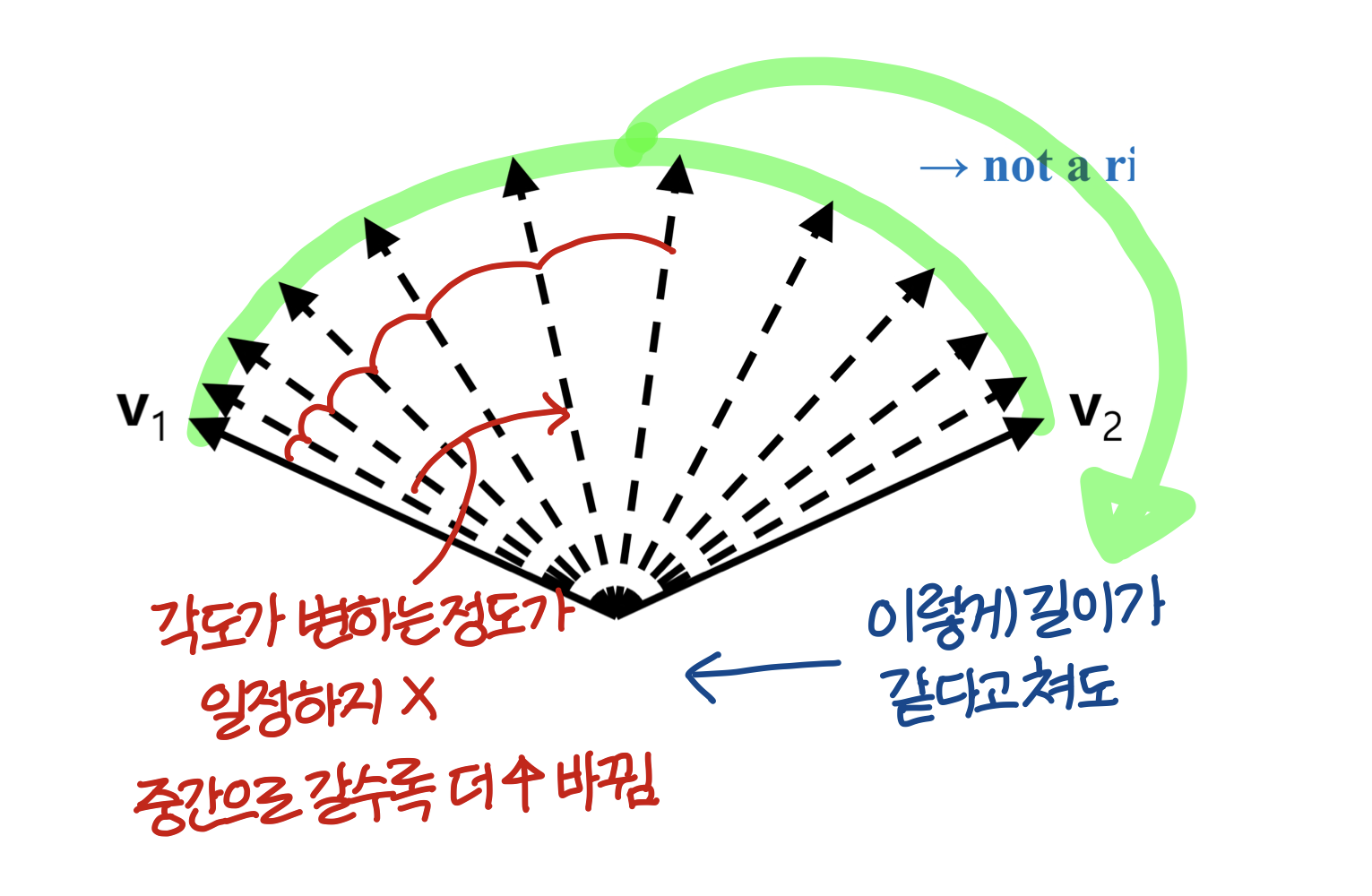
Interpolating Rotation Vector
rotation vector에 대해선 어떨까?? 이건 linear Interpolating 해도 괜찮을 것 같은데???
- 같은 길이의 rotation vector v1, v2가 있을때
v1과 v2를 linear interpolating 해서 나올 수 있는 벡터들을 살펴보면
→ 즉, 이건 올바른 방법이 아니다.
Interpolating Euler Angles
Euler angles (알파, 베타, 감마) 이렇게 표시하는데
→ Euler angles의 두 tuple을 Interpolating 하더라도 올바른 결과가 안나온다.
→ 짐벌락 문제도 여전히 생김
Slerp
올바른 방법은 Slerp이라는 방법이다!
- Spherical linear interpolation의 약자
- 두 orientation을 Linear interpolating 하는 방법이다.
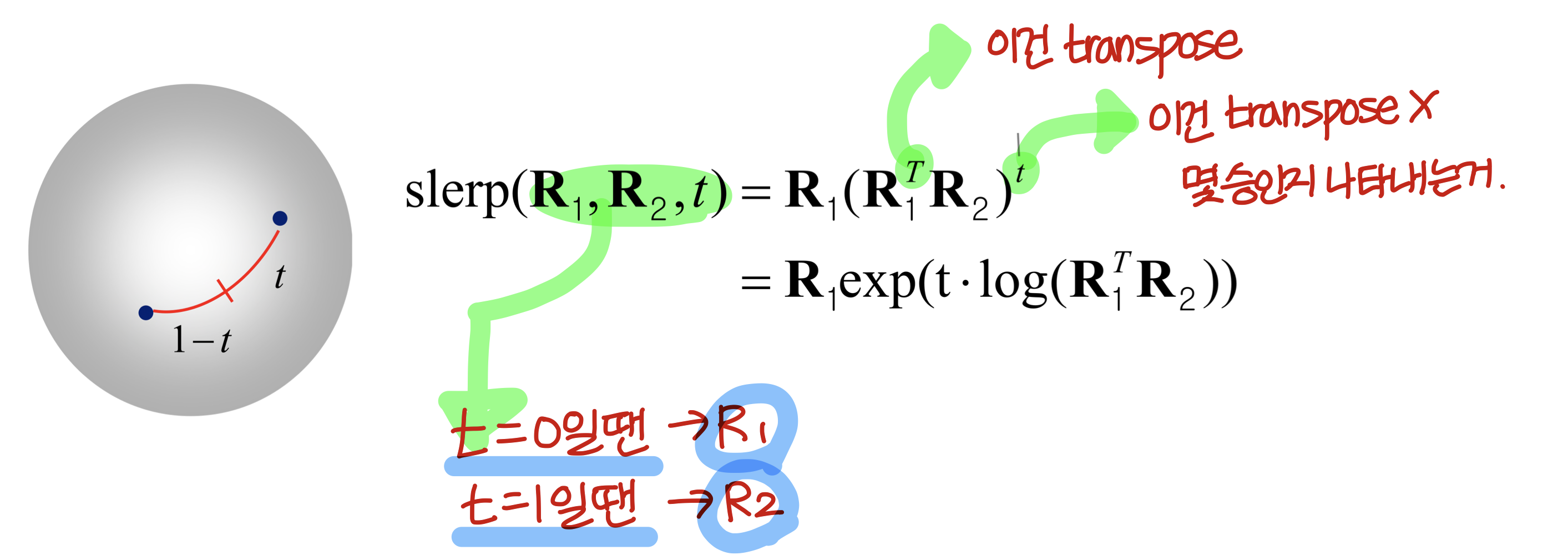
의미를 생각해보면
Quiz #3

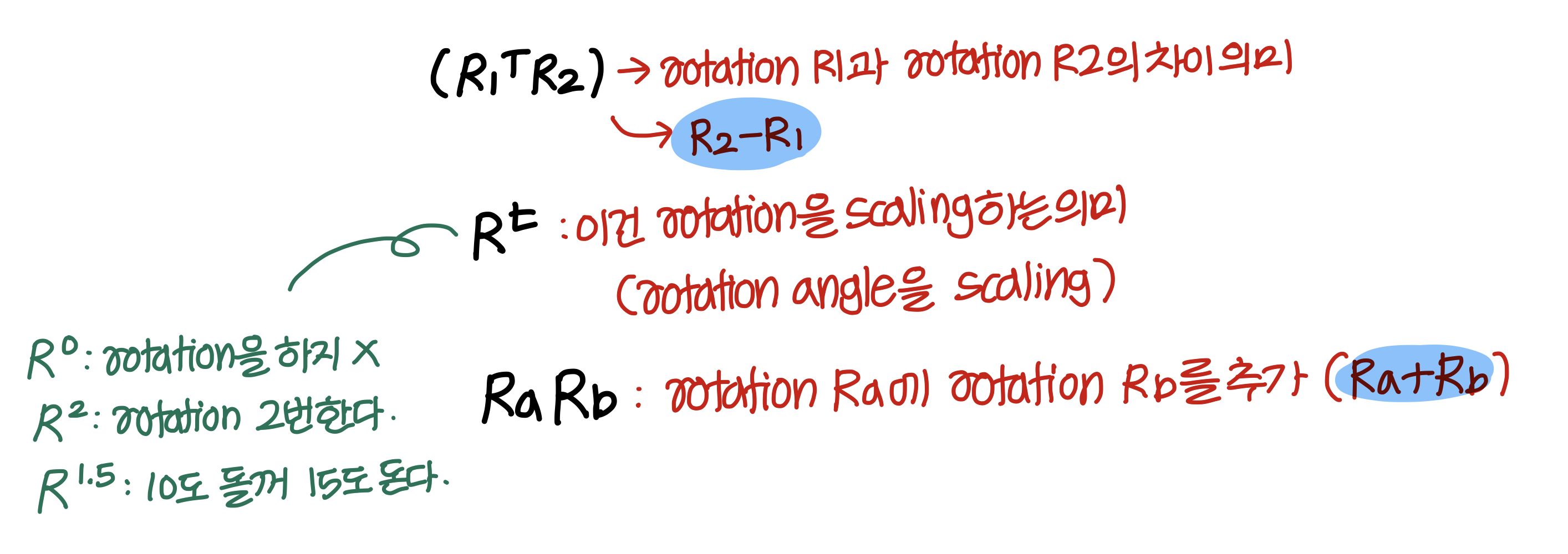
R1에 대해 정의되어 있는 frame을
R2에 대해 정의된 frame과 일치하게 만들고싶은거
R1 @ X = R2
가 되도록 하는 X를 찾아야한다.
→ applied w.r.t. the frame R1: frame R1에 대해 적용했다는 마지막 줄 때문에
만약 global frame에 대해 적용되는 rotation matrix를 찾으라고 했다면 왼쪽에 썼을거임.
따라서 답은 x = R1.T @ R2
Uploaded by N2T