overview
Diffusion Model은 data를 만들어내는 deep generative model 중 하나로, data로부터 Noise를 조금씩 더해가면서 data를 완전한 Noise로 만드는 1) Forward diffusion process와 이와는 반대로 Noise로부터 noise를 조금씩 제거해나가면서 입력 data와 유사한 확률 분포를 가지는 결과 data를 생성해나가는 2) reverse diffusion process를 활용한다.


위의 그림에서 x_0가 원본 data이며 forward diffusion process에서는 여러 단계에 걸쳐 noise를 추가해나가며 완전한 noise x_T를 만들어낸다. reverse diffusion process에서는 x_T로부터 Noise를 제거해나가 data를 복원해나간다.
이때 forward diffusion process에서는 고정된 정규분포(=Gaussian 분포)로 생성된 Noise가 더해지게 되고, reverese diffusion process에서는 이미지를 학습된 정규분포로 생성된 Noise를 제거한다.
즉, diffusion model이 풀려고 하는 문제는,
Forward -> Reverse 단계를 거친 '결과 이미지'를 '입력 이미지'의 확률 분포와 유사하게 만드는 것이다. (random noise로부터 실제 data와 유사한 data를 generate하는 것이 가능하도록)
이를 위해 Reverse단계에서, Noise 생성 확률 분포 Parameter인 평균과 표준편차를 업데이트하며 학습이 진행된다. 그럼 forward diffusion process와 reverse diffsuion process를 자세히 살펴보자.
Forward diffusion process
위에서도 간단히 언급했지만 forward diffusion process q는 data(x_0)로부터 noise를 더해가면서 최종 noise(x_T) 형태로 가는 과정이다. 이 과정의 분포를 알아내야하는 이유는, reverse diffusion process의 학습을 forward diffusion process의 정보를 활용해서 하기 때문이다. forward process는 data에 Gaussian noise를 조금씩 더하는 Markov chain의 형태를 가진다.
식으로 표현하면 다음과 같다.
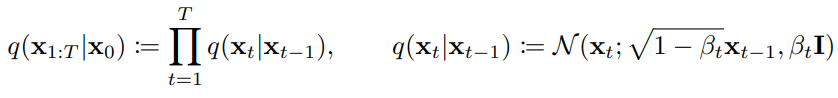
이전 상태(x_{t-1})가 주어졌을 때 현재 상태(x_t)가 될 확률 분포 q는 평균(μ)과 분산(Σ)으로 구성된 Gaussian Distribution(N= Normal Distribution)을 따른다. 이 식은 Noise의 크기인 parameter β를 포함한다. 다르게 표현하면, 이전 상태(x_{t-1})에서 이미지가 β 만큼 다른 data을 선택하게 되고 root(1-β)만큼 이전 data를 선택한다고 생각하면 된다.
foward 과정에서 β는 고정되어 있지만 확률분포에 따라 Noise를 더해주기 때문에 마지막 상태(x_t)의 결과는 항상 다를 수 있다.
Reverse diffusion process
Reverse diffusion process에서는 마지막 상태(x_t)에서 최초 상태(x_0)를 만들고자 한다. 만약 위에서 정리했던 q(x_t | x_{t-1})에서 좌측항과 우측항을 바꾼 조건부 확률 q(x_{t-1} | x_t)를 알 수 있다면, 최초 상태(x_0)를 만들 수 있지만, 이는 계산할 수 없다. 따라서 확률 분포 q가 주어졌을 때 이 확률 분포를 가장 잘 모델링하는 확률 분포 pθ를 찾아야한다.
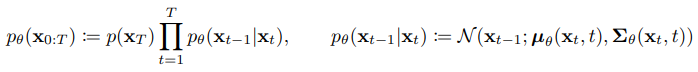
위의 식에서 각 단계 정규분포의 평균(mu θ)과 표준편차(sigma θ)는 학습되어야하는 parameter이다. 그리고 위 식의 시작지점인 noise의 분포는 다음과 같이 가장 간단한 평태인 표준정규분포로 정의한다.
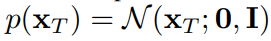
Training
이제 Forward diffusion process와 reverse diffusion process가 무엇인지 이해했으니 reverse diffusion process의 parameter의 추정을 위해 diffusion model의 학습을 어떻게 진행하게 되는지 알아보자. 실제 data의 분포인 p(x_0)를 찾아내는 것이 Generative model의 목적이기 때문에 이 likelihood를 최대화 하는 것이 학습의 목적이다.
Loss에 대한 이해를 돕기 위해 전체 구조를 아래와 같이 그렸다.
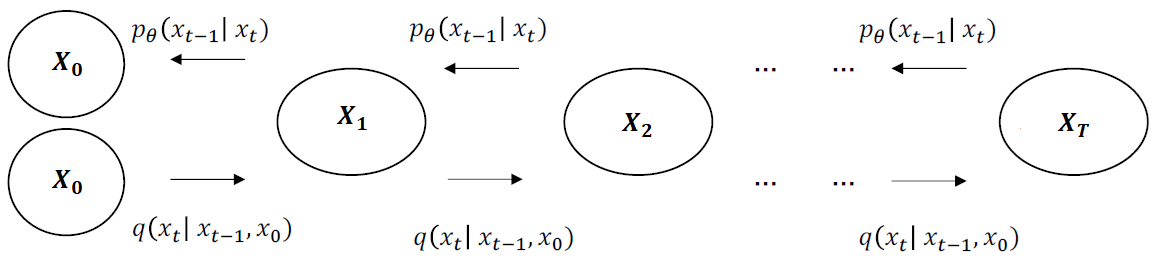
그리고 Loss 수식을 깔끔하게 재정리하면 아래와 같다. 아래의 값을 최소화하는 방향으로 학습을 진행해야한다.
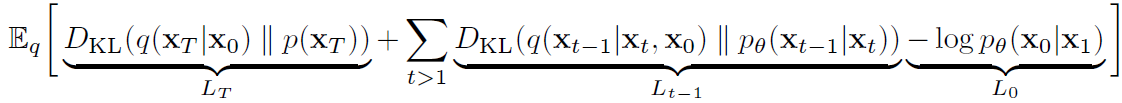
- LT : 마지막 상태(x_T)에 대해 확률 분포 q와 p의 KL divergence를 최소화하여 p와 q의 확률 분포 차이를 줄일 수 있다. 즉 p가 generate 하는 noise x_T와 x_0가 주어졌을 때 q가 genearte하는 noise x_T 간의 분포차이를 의미하며 regularization loss라고 불린다.
- L{t-1} : 현재 상태(x_t)가 주어졌을 때, 이전상태 (x_{t-1})가 나올 확률 분포 q와 p의 KL divergence를 최소화하는 term으로, p와 q의 확률 분포 차이를 줄일 수 있다. 즉, reverse process와 forward process의 분포 차이를 의미하며 denosing process loss라고 부른다.
- L0 : VAE loss를 구성하는 Reconstruction loss (-log( p(x0|xT))와 식이 대응된다. latent x_1으로부터 data x_0을 추정하는 likelood인 log(p(x0|x1))를 최대화하여 p와 q의 확률분포 차이를 줄일 수 있다.
참고문헌)
https://process-mining.tistory.com/182
Diffusion model 설명 (Diffusion model이란? Diffusion model 증명)
Diffusion model은 데이터를 만들어내는 deep generative model 중 하나로, data로부터 noise를 조금씩 더해가면서 data를 완전한 noise로 만드는 forward process(diffusion process)와 이와 반대로 noise로부터 조금씩 복
process-mining.tistory.com
[개념 정리] Diffusion Model
GAN, VAE 와 같은 생성 모델(Generative Model) 중 하나로써, 2022년에 이슈가 되었던 text-to-image 모델인 Stable-Diffusion, DALL-E-2, Imagen의 기반이 되는 모델입니다. 많은 논문에서 Diffusion Model이 인용되지만 수
xoft.tistory.com
https://ffighting.net/deep-learning-paper-review/diffusion-model/diffusion-model-basic/
Diffusion Model 설명 - 기초부터 응용까지
Diffusion Model의 기초부터 응용까지 살펴봅니다. 기초 부분에서는 Diffusion Model의 동작 방법, Architecture, Loss Function을 살펴봅니다. 응용 부분에서는 다양한 Diffusion Model을 알아봅니다.
ffighting.net
'수업정리 > 딥러닝 이론' 카테고리의 다른 글
| Batch normalization vs Input normalization 이해하기 (1) | 2023.11.23 |
|---|---|
| Residual Network, Residual Block 개념정리 (0) | 2023.10.16 |
| Autoregressive Learning (0) | 2023.08.24 |
| 딥러닝 수업정리) 15_Word embedding (2) | 2023.06.13 |
| 딥러닝 수업정리) 16_Transformer (2) | 2023.06.13 |
